V nedávné době se zahraničními populárně-vědními servery prohnaly informace o studiu systémů, které dosahují záporné teploty v Kelvinově stupnici a dostaly se i na české stránky. Pojem záporná teplota je v tomto případě velice specifický a do značné míry „formálně“ zavedený. U toho, kdo přesně neví proč a jakým způsobem byl definován a má spíše „klasické“ znalosti o teplotě, mohou podobné populární články vést k velmi zavádějícím představám. Proto bych se pokusil o osvětlení některých pojmů a dějů, které jsou s touto oblastí spojeny.
Pojem teplota
Teplota je fyzikální veličina, která kvantitativně popisuje to, co běžně člověk pociťuje jako horko nebo chlad. Teplota je spojená s tepelnou energií, kterou systém (objekt) má, která je v klasickém případě vlastně kinetickou energií náhodného pohybu částic, které jej tvoří. Rozdíl či rovnost teplot tak určuje, ze kterého tělesa na které bude probíhat přenos tepla nebo případně nastane termodynamická rovnováha. Existuje pak několik přístupů, které umožňují získat vysvětlení (definici) teploty. Lze vyjít z klasického termodynamického popisu empirických veličin měřených v laboratoři. Další možnost vychází z již zmíněné souvislosti teploty s kinetickou energií chaotického pohybu částic daného systému. Absolutní teplota je pak mírou vnitřní energie ideálního plynu (pro nižší teploty komplikovanějšího systému). Následující přístup je pak založen na statistické fyzice. Zde se vychází z pojmu možných rozlišitelných mikrostavů, kterými lze realizovat daný pozorovaný makroskopický stav. Často je třeba zapracovat i kvantovou teorii.
Ve všech těchto přístupech dostaneme nejnižší možnou hodnotu teploty, která je v absolutní stupnici označená jako absolutní nula. Ta je spojena s nejnižší možnou hodnotou vnitřní energie systému. Pro ní je rovna nule také hodnota entropie. Třetí termodynamický zákon říká, že žádný systém nemůže dosáhnout této absolutní nuly a můžeme se k této teplotě jenom limitně přibližovat.
Před chvíli jsme zmínili entropii. Tato veličina bude důležitá v dalším povídání, tak si ji trochu připomeneme. Byla zavedena jako termodynamická veličina pomocí tepla a teploty. V uzavřeném systému může entropie pouze růst. Kromě termodynamické definice ji můžeme definovat i statisticky. Ne úplně korektně se někdy označuje jako míra neuspořádanosti. Čím je stav více uspořádaný, tím je méně pravděpodobný a má nižší entropii. S vyšší mírou neuspořádanosti stoupá i pravděpodobnost stavu a jeho entropie. Platí, že při zvětšování vnitřní energie roste i entropie. Teplotu tak můžeme určovat právě i pomocí těchto veličin.
Zatím jsme se věnovali systémům složených z velkých souborů částic, popsaných klasickou termodynamikou. Tyto navíc odzrcadlují „běžnou“ lidskou zkušenost s teplotou. Odpovídají základnímu chápání rozdílu mezi studeným a teplým. Splňují předpoklad, že teplo přechází ze systému s vyšší teplotou do systému s nižší teplotou. Teploty absolutní nuly nelze ani dosáhnout a už vůbec nenastávají teploty pod nulou. Platí, že o teplotě se dá hovořit jen u systémů složených z velkých statistických souborů a je třeba, aby bylo možné dosahovat termodynamické rovnováhy.
Kvantové systémy
Pokud se dostaneme k velmi nízkým teplotám, začíná řada problémů i zajímavých možností s teplotou spojených. Teprve teď se přibližujeme k oblasti, které se chceme věnovat, kde se ale dostáváme už za hranici běžných znalostí i vzdělanějšího čtenáře. Je nevyhnutné si uvědomit, že vnitřní energie částic není jen energií spojenou s náhodným pohybem. Navíc jsou hodnoty energie kvantované a je třeba brát v úvahu kvantové vlastnosti systému. Zobecněnou teplotu tak můžeme díky statistickému přístupu definovat i pro takové kvantové systémy, které obsahují pouze omezený počet diskrétních energetických hladin s nějakou minimální a maximální hodnotou energie. Musí však jít o systém, který jen velmi málo ovlivněn stupni volnosti spojenými s „klasickou“ teplotou (třeba chaotický pohyb). Taková zobecněná teplota se dá použít i pro systém malého počtu stupňů volnosti (částic). Její definici můžeme založit i na obsazenosti příslušných diskrétních stavů.
Záporná teplota
A to je právě ten specifický případ, kdy lze zavést pojem záporné teploty. Lze ji tak mít pouze u kvantových systémů, které mohou dosáhnout jen omezený počet diskrétních energetických stavů. Mohou mít však i omezený (malý) počet částic. To je například případ, když budeme mít v magnetickém poli částice se spinem. U takového systému hovoříme o spinové teplotě. Můžeme třeba předpokládat, že máme jen dvě možné diskrétní hodnoty energie. Pokud jde o fermiony se spinem 1/2, budou mít dvě možné projekce spinu v magnetickém poli, ve směru intenzity magnetického pole a ve směru proti. Taková částice má se spinem i magnetický moment. Chová se tak jako malá magnetka. Jedna orientace spinu (magnetického momentu) vůči magnetickému poli bude energeticky výhodnější než druhá. Máme tedy dvě hodnoty energie. Důležité pro možnost hovořit v tomto případě o teplotě je, aby si částice předávaly orientaci spinu a energii s tím spojenou. Pokud změní jedna částice energeticky náročnější spinovou orientaci na méně energeticky výhodnou, uvolní se přesně taková energie, aby jiná částice, která ji převezme, změnila spinovou orientaci v opačném směru. Tato předávání orientace a energie musí probíhat dostatečně rychle, aby se v systému mohl nastolit stav termodynamické rovnováhy s definovanou spinovou teplotou. Jedná se o analogii předávání energie ve srážkách atomů (molekul), které vede k termodynamické rovnováze v systému s klasickou teplotou.
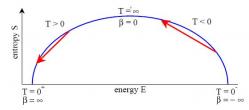
Pokud bychom měli všechny částice „zamrzlé“ v energeticky nižším stavu, měli bychom nulovou teplotu a také nulovou entropii (systém je plně uspořádaný a existuje jediný mikrostav, kterým můžeme dostat daný makroskopický stav. Pokud budeme dodávat systému energii, poroste entropie i teplota. V určitém okamžiku, když máme přesně polovinu částic v nižším a polovinu ve vyšším energetickém stavu, dosáhne entropie maximální hodnoty a s dalším dodáváním energie začne klesat. Teplotu definovanou pomocí entropie v případě, že entropie s růstem energie klesá, dostáváme „formálně“ jako zápornou. S dalším dodáváním energie tak klesá entropie a zmenšuje se velikost záporné teploty. V případě, že by se nám podařilo dodat tolik energie, abychom zamrazili všechny částice do spinové orientace s vyšší hodnotou energie, tak by byla opět nulová entropie. A také nulová teplota, tentokrát však dosažená ze záporné strany. I v tomto případě se však můžeme k této hodnotě jen limitně přibližovat.
Je třeba zdůraznit, že k záporným malým spinovým teplotám se dostáváme přes nekonečně velkou kladnou a nekonečně velkou zápornou hodnotu, které se stýkají v místě, kde entropie přestane růst a začne klesat. Záporné teploty jsou tak nad kladnými, teplo se přenáší od systému se zápornou teplotou k systému s kladnou teplotou. Systém se zápornou teplotou je tak teplejší než systém
s kladnou teplotou. Seřazení teplot je tak 0 K, …. 500 K, …+∞ K = -∞ K, … , -500 K, … 0 K. Je pochopitelně možné i předefinovat pojetí, co je chladnější a co teplejší tak, aby záporné teploty předcházely na ose teploty kladné a v pořadí od -∞ K → 0 K, ale bylo by to daleko nepřirozenější a více zavádějící. Jestliže ponecháme první, přirozenější definici, zachová se ta vlastnost, že pokud se dostanou do kontaktu systémy s různými teplotami, teplota, která se ustálí po dosažení tepelné rovnováhy, bude ležet mezi nimi. Budu-li mít dva systémy v kontaktu, z nichž jeden bude mít teplotu 300 K a druhý -300 K, může být teplota dosažená při tepelné rovnováze jak 1000 K tak i -1000 K, ale nikdy ne 5 K nebo -5 K. Velice pěkný přehled problematiky publikoval už v roce 1956 Norman F. Ramsey s rozsáhlým seznamem odkazů. Dovolil bych si ještě zdůraznit, že negativní teploty nemusí být spojeny jen se spinovými teplotami, ale obecně se systémy, kde dochází ke změně závislosti změny entropie při růstu energie, tedy entropie začne s růstem energie klesat. Požadavky, které musí takový systém splňovat, už jsme zmínili. Nejsnadněji však lze tyto nutné podmínky splnit u kvantového systému částic se spinem.
Jak systémy se zápornou teplotou zrealizovat
Podívejme se nyní, jak lze prakticky takový systém v laboratoři realizovat. Jednou z možností je umístění atomových jader v silném magnetickém poli. V okamžiku, kdy se ustaví rovnováha, kdy je velká většina jader v nízkém energetickém stavu, obrátíme orientaci magnetického pole. Dostaneme tak situaci, kdy je většina jader v energeticky vyšším stavu. A v době, než dojde ke změně orientace jader v magnetickém poli, máme a můžeme zkoumat systém se zápornou teplotou. Je třeba zdůraznit, že většina experimentů s orientacemi spinu jader se provádí při velmi nízkých klasických teplotách. A jak už bylo zmíněno, je potřeba zajistit, aby docházelo k co nejmenšímu přenosu energie mezi spinovými a kinematickými stupni volnosti. Tedy, aby energie nám od spinových stupňů volnosti unikala jen pomalu a spinová teplota se měnila chladnutím systému od záporných teplot ke kladným co nejpomaleji. Již v padesátých letech se studovaly například jaderné spinové systémy, které byly založeny na velice čistých krystalech fluoridu lithného LiF. V tomto případě však jde o velmi jednoduchý systém jen s velmi omezeným počtem energetických hladin.
Proto je snaha získat složitější a zajímavější systémy s negativní teplotou. A právě realizaci takového systému, i když zatím pouze teoreticky, navrhl Achim Rosch s kolegy. Je založena na dřívější práci Allarda Moska. Ten navrhl zkoumat systém hluboce ochlazeného plynu zachyceného pomocí laseru do pasti v magnetickém poli. Laserem se „natlačením“ plynu do těsné koule vytvoří kondenzát s velmi vysokou mírou uspořádanosti a tedy nízkou entropií. Laserem se vytváří podmínky pro energeticky výhodný stav. Potom se činnost laseru změní tak, že bude působit ve směru „rozehnání“ kondenzátu. Kombinace vlivu laseru a magnetického pole může totiž mezi atomy vytvářet odpudivé nebo přitažlivé síly. Zatímco před změnou byla většina atomů v energeticky nejméně náročném stavu, po změně jsou naopak v tom energeticky náročném. Navíc, pokud odebereme nějaké částice v energeticky náročném stavu, tedy snížíme energii systému, poměr mezi atomy ve vyšším a nižším energetickém stavu se více přiblíží jedničce a entropie (míra neuspořádanosti) tak vzroste.
Dostáváme tak systém, ve kterém s ubíráním energie entropie roste a s dodáváním energie klesá. Což je opačně než v klasickém systému a máme tedy systém s negativní teplotou. V něm další snižování absolutní hodnoty teploty (přibližování k absolutní nule ze strany záporných teplot) lze naopak odebíráním atomů s nejnižší energií. Rovnováha takového systému je však velice nestabilní. To je důvod, proč se využívá další systém laserů, který vytváří v systému „optickou mřížku“, která pomáhá udržovat systém v nestabilním rovnovážném stavu. Velmi důležitým doplněním Achima Rosche je návrh, který by pomohl identifikovat vznik popsaného systému s negativní teplotou. Měřila by se rychlost atomů opouštějících systém. Díky větší energii atomů v systému s negativní teplotou by tato rychlost těchto atomů byla vyšší.
Závěr
Vidíme, že existují velice zajímavé systémy, které mají zápornou teplotu. Ovšem tato teplota je specificky definována a má dost rozdílné vlastnosti, než jaké teplotě přisuzuje běžný čtenář. Dochází například k tomu, že systém se zápornou teplotou je teplejší než ten s teplotou kladnou. A tepelná energie samovolně přetéká se systému se zápornou teplotou do systému s teplotou kladnou. Ač se jednoduché systémy s negativní teplotou, využívající orientaci spinu atomových jader v silném magnetickém poli, studují už od padesátých let, teprve nedávno se objevuje teoretický návrh na přípravu a výzkum daleko komplexnějšího systému. Je teď na experimentátorech, aby jej realizovali.
Protože termodynamika není mou hlavní specializací, omlouvám se za případné nepřesnosti a zjednodušení. Ty však mohou být zdrojem pro zajímavou diskuzi pod článkem.
Pro podrobnější informace lze nahlédnout do originálních prací: (Physical Review Letters 1 a 2 nebo arXiv:1008.0468v2).
