Na úvod si dejme drobnou rekapitulaci a optimistický výhled na problematiku vesmírného výtahu.
Počátky
Počáteční idea vesmírného výtahu se datuje od 60tých let minulého století. O té doby byla tato myšlenka dále rozvíjena a předkládána veřejnosti jako například v díle Atrhura C. Clarke – Rajské fontány (1979), formou mnoha knižních derivátů, televizních děl a několika počítačových her. Nechme nyní beletrii a zábavní tvorbu poněkud stranou a pojďme se podívat jak na realitu vesmírného výtahu pohlíží svět fyziky.
Umístění výtahu v gravitačním poli Země
Umístěme počátek souřadného systému do středu Země a nechme ho rotovat rychlostí jedné otáčky za den, pak následující rovnice popisuje zrychlení pro vybraný statický bod nacházející se v rovině řezu Zemí v rovníku:
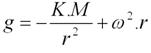
Kde:
g je zrychlení podél poloměru (m.s-2),
K je gravitační konstanta (m3.s-2.kg-1.)
M je hmotnost Země (kg)
r je vzdálenost od tohoto bodu do středu Země (m),
ω je rychlost rotace Země (y-2).
Zrychlení na Zemském povrchu vypočítáme následovně:
![]()
a po úpravě dostáváme
.
![]()
V určitém bodě nad rovníkem se pak odstředivá a gravitační síla ruší a dostáváme geosynchroní trajektorii ve výšce 42,164 km (měřeno od středu Země).
![]()
nebo po dosazení
.
![]()
Z tohoto nám vychází, že část lana pod geostacionární stanicí bude urychlována směrem k Zemi a lano nad ní bude urychlováno směrem do vesmíru. Pokud by bylo lano spuštěno dolů k Zemi, pak musí být samozřejmě správně vyváženo na stranu od Země. Jakmile by došlo k ukotvení volného konce lana k Zemi posunutím zátěže dále od centra rovnováhy, dosáhli bychom jeho napnutí. Toto lano by pak mohlo být použito jako výtah.
Teorie nosného lana
Hlavním technickým problémem takového lana vyrobeného z současně dostupných materiálů a majícího stejný průměr po celé své délce je, že by se přetrhlo vlastní vahou. Řešením je následující differenciální rovnice:
σ*dS = g*ρ*S*dr
g je zrychlení podél poloměru (m.s-2)
S je plocha kabelu v jakémkoliv bodě r (m2) dS a jeho variace (m2)
ρ je hustota materiálu použitého pro kabel (kg.m-3)
σ je mez pružnosti materiálu (Nm-2 = kg.m-1.s-2)
Tato rovnice říká, že v každém bodě lana musí být násobek meze pružnosti s danou plochou roven aktuálnímu gravitačnímu zrychlení působícím na hmotu lana.
Po dosazení za g z původní rovnice dostaneme následující (pro vzdálenost z povrchu Země na geostacionární dráhu):
![]()
a další úpravě:
![]()
kde x = ω2*r0 / g0
je poměr mezi odstředivou silou působící na rovníku a silou gravitační. Z těchto dvou rovnic je patrný zásadní vliv poměru g0*r0, tedy poloměru Země a gravitačního zrychlení na průměr lana. Dalším poznatkem je vliv odstředivé síly vyvolané rotací Země ve výsledku snižující nároky na pevnost lana přibližně o jednu třetinu.
Materiál Lana
Druhým technickým problémem je, že nároky na materiál lana dané součinitelem g0*r0 jsou jednoduše příliš velké. Námáhání lana roste s jeho délkou v gravitačním poli exponenciálně. Na úrovni Zemského povrchu pak máme:
g0.r0 = 62,5 106 m2.s-2 (nebo J / kg)
ρ = 5 103 pro většinu pevných látek, takže požadovaná mez pružnosti materiálu σ je například:
σ ~ 300 109 kg.m-1.s-2.
To odpovídá kabelu z materiálu schopného při průřezu jednoho čtverečního milimetru unést v gravitačním poli Země (ve výšce 0m n.m.) náklad o váze 30 t.
Jakou nosnost tedy musí mít lano pro vesmírný výtah?
Na předchozích rovnicích jsme si ukázali, že nosnost lana není jediným parametrem vstupujícím do hry. Pokud by bylo takové lano konstruováno z oceli, tak by v místě vyrovnání gravitační a odstředivé síly mělo průřez asi poloviny Zemského průřezu na rovníku. Pro zjednodušení popisu potřebného materiálu vědci zavádí jednotku zvanou Yuri – specifickou nosnost materiálu. O jednotce Yuri jsem se již zmínil v článku Výsledky vesmírných výtahových her pro rok 2009, připomeňme si že tato jednotka je poměrem pevnosti v tahu vůči své hmotnosti:
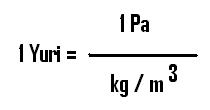
Z předchozích rovnic nám pak vychází, že by stavba výtahu byla reálná s materiálem o hodnotách 40-50 Yuri (např. mez pružnosti 88-110 GPa, při podélné hustotě 2 g/m). Uváděná hodnota je již včetně bezpečnostních koeficientů a částečně zohledňuje i další vstupní parametry jako je výkon zdviže, návratnost projektu, jeho obslužnost a jiné, které si rozebereme příště. Prozatím berme toto číslo jako jakousi optimální hodnotu, která nám umožní se dostat k možným návrhovým číslům.
Udělejme si odbočku do Japonska k fyzikovi Sumio Iijima, jehož objev poprvé rozvířil diskusi nad možností přepravy materiálu vesmírným výtahem na oběžnou dráhu Země. Pan Sumio Iijima totiž počátkem 90tých let minulého století publikoval vědeckou práci na téma uhlíkových nanotrubiček (Carbon Nano Tubes – CNT), na jejímž základě se myšlenka vesmírného výtahu posunula ze stránek beletrie na rýsovací prkna inženýrů.
Uhlíkové nanotrubičky (Carbon Nano Tubes – CNT)
Úvodní výpočty a počítačové simulace naznačovali že nanotrubičky by měli vydržet až 50 GPa (22 Yuri) v tahu, což bylo následně potvrzeno i experimentálně. Další prostorové configurace CNT by měli teoreticky dosahovat pevnosti 126 GPa (57 Yuri) a poslední výzkumy zatím končí vícestěnnými CNT (MWNT) a jejich teoretickou pevností až 150 GPa (68 Yuri).
Vraťme se zpět k problematice vesmírnému výtahu. CNT by nám podle výpočtů a simulací měly poskytnout pevnost v tahu až 68 Yuri (150 GPa). V předešlých odstavcích jsme si také ukázali, že požadavky na stavbu se pohybují mezi 40-50 Yuri. Teď si položme otázku, proč tedy vesmírný výtah za uplynulých 20 let nebyl nepostaven, nebo se o jeho konstrukci alespoň někdo nepokusil?
Co se z počátku zdálo jako být jasnou záležitostí se totiž posléze začalo zásadně komplikovat. Prvním problémem bylo vytvořit uhlíkové nanotrubičky dosahující délky vyšší několika milimetrů. O několik let později se k tomuto problému přidává vysoká náchylnost CNT k narušení stěn a to jak při výrobě, tak při namáhání samém. Důsledkem je snížení nosnosti o závratných 75 %. Pokud teď vezmeme vypočtenou specifickou nosnost vícestěnných CNT (68Yuri) a odečteme zmiňovaných 75 % dostáváme hodnotu 17 Yuri, která je výrazně nižší než potřebných 40 Yuri.
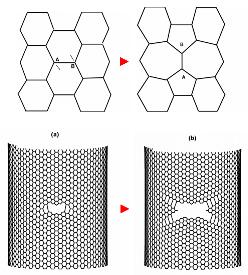
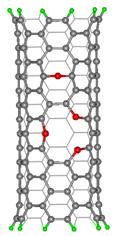
Porušená stěna CTN a šíření “oka”.
Nyní si opět položme otázku, proč tu již není vesmírný výtah? Odpověď by teď měla být poměrně jednoduchá a od dob A. C. Clarka se ani moc nezměnila. V současnosti nedisponujeme známým materiálem, který by mohl být použit na konstrukci výtahového lana. Problémem je, že naděje vkládané do uhlíkových nanotrubiček byly prozatím liché a zatím neznáme jiný materiál s vhodnějšími vlastnostmi. Nejdelší vytvořená nanotrubička se nyní stále měří spíše v milimetrech než požadovaných stovkách kilometrů a problémy s narušením jejich stěn se zatím nedaří řešit. Dalším problémem je absence potřeby materiálu těchto parametrů v běžné průmyslové výrobě, kromě teoretické potřeby vesmírného výtahu, což omezuje přirozené investice do výzkumu v tomto oboru. Jediným motivátorem je NASA pořádající vesmírné výtahové hry, ale i přes štědrou odměnu se soutěžící do této disciplíny nehrnou. Můžeme jen doufat, že v budoucnu dojde k technologickému pokroku, který nám konstrukci výtahu umožní. V současnosti však tato stavba reálná není.

Soutěžní páska Japonského týmu z Vesmírných výtahových her pro rok 2008, po testu.
Abychom nekončili příliš depresivní nótou, tak předesílám, že si v příštím díle rozebereme uvažované možnosti napájení zdviže, problémy vibrace lana způsobené jeho ukotvením i atmosférickými vlivy a pravděpodobnost kolize s odpadem na oběžné dráze. Ač se tyto problémy mohou zdát zásadní, tak jejich navrhovaná řešení jsou technicky velmi zajímavá a dávají šanci na úspěch.
Další příklady poruch ve stěnách CNT:
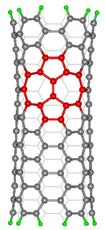
Porucha nazývaná “kamenná zeď”
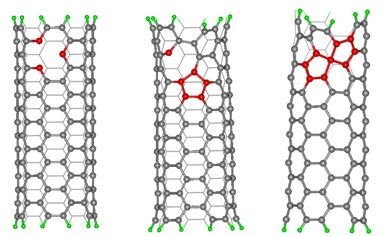
Další možné poruchy stability ve stěně.
Porucha nazývaná “Přeskupení atomu“

Trocha humoru z kuchyně „vesmírného výtahu“ (ref. https://www.imdb.com/title/tt0468999/).
V reakci na komentáře uvedené pod článkem bych chtěl uvést následující upřesnění a doplnění:
V odstavci "Teorie nosného lana" - differenciální rovnice σ*dS = g*ρ*S*dr - řeší podmínku sigma=konst., právě přechodem k profilaci jeho průřezu S po dělce lana. SIGMA v diferenciální rovnici pro délkový element není mez pružnosti, nýbrž je to mezní přípustné napětí v tahu. Tato rovnice říká, že každý úsek lana něco váží a tak mu k jeho průřezu na jeho horním konci přidáme i přírůstek průřezu právě tak velký, aby pokryl tíhu toho úseku. Tím nám bude průřez s výškou růst, alespoň tedy až do místa, kde se otočí znaménko zrychlení (na té geostacionární orbitě). A za cenu růstu průřezu se umožní to, aby se napětí materiálu udržovalo na nějaké vhodné velikosti, nejlépe konstantní a rovné přípustnému maximu (se zahrnutím nějaké bezpečnosti). To je cesta k efektivnímu využití materiálu (Jiří Zbytovský).
Detailně je výpočet uveden na https://www.zadar.net/space-elevator/ (Petr K).
Zdroje:
https://www.spaceelevatorblog.com
https://www.spaceelevatorgames.org
https://www.lasermotive.com/blog/?p=489
https://cosmiclog.msnbc.msn.com/archive/2009/08/17/2033079.aspx
https://www.spaceward.org/documents/papers/The%20Space%20Elevator%20Feasibility%20Condition.pdf
https://io9.com/5206012/this-space-elevator-is-the-terrorists-next-target
https://www.pcworld.com/article/170199/space_elevator_science_fiction_or_global_warming_cure.html
https://www.redorbit.com/news/space/1563762/japan_looking_to_build_worlds_first_space_elevator/
https://en.wikipedia.org/wiki/Carbon_nanotube#Defects
https://fy.chalmers.se/OLDUSERS/fengding/CNTs.htm
https://en.wikipedia.org/wiki/Space_elevator