Logika je způsob, jak poznat, zda se z určitých faktů dá spolehlivě určit pravdivost něčeho dalšího, případně zda je to nemožné. Důležitou roli přitom hrají vzájemné vztahy těchto faktů, základním nástrojem jsou tedy různé způsoby spojování základních jednoduchých faktů (výroků). Možností, jak základní fakta spojovat, je mnoho, ale z praktického hlediska stačí umět pět operací: negaci, logické "a", logické "nebo", implikaci a ekvivalenci. (Mimochodem, některé obory dávají přednost jiným logickým spojkám, například obvodáři dokázali dělat zázraky s věcí zvanou "nand".) Z teoretického pohledu stačí dokonce méně, třeba jen negace a "nebo", ale vyjadřování různých logických konstrukcí je pak neprakticky komplikované. Těch pět operací je tedy jakýmsi kompromisem, abychom jich neměli moc, zároveň abychom neměli moc komplikované výrazy a přitom jsou přirozené.

 

První tři z těch pěti tady budu neférově ignorovat, protože jsou v zásadě jasné a zas tolik se nad nimi mudrovat nedá. Zato druhé dva jsou z pohledu praktického používání velice zajímavé, protože umožňují dělat úsudky. Na ně se tedy podíváme.

 

Co je to implikace?
Dva výroky p a q jsou spojeny implikací, když je zapíšeme formálně takto: p => q. Čteme to nejčastěji "Jestliže p, pak q," ale jsou možná i jiná vyjádření, třeba "p implikuje q", o dalších se zmíníme dále. Příklady: "Jestliže prší, tak je srpen." "Jestliže je úterý, pak jsme v Belgii" (tohle je mimochodem název jedné docela dobré komedie).

 

Jak vidíme z těch příkladů, spojovat se dá všechno, ale ne každá takto vytvořená implikace je "správná". Implikace se prohlásí za pravdivou, pokud kdykoliv, když je splněn její předpoklad p, musí být automaticky vždy a bez výjimky pravdivý i její závěr q, ať už se děje cokoliv, i kdyby žáby z nebe pršely a všichni politici se přes noc poctivými stali. Asi se shodneme, že ty dva příklady výše nejsou pravdivé implikace. Abychom mohli ilustrovat různé logické triky, zvolíme si teď jednu pravdivou implikaci jako příklad. Spousta se jich najde v matematice, ale vzhledem k všeobecné oblíbenosti dotyčného oboru bych s tím nerad provokoval (ale nedalo mi to, jednu pěknou zkusím rozebrat na závěr jako bonus). Myslím, že se snad shodneme, že tato platí:

 

(I )   Jestliže ze Země odfouknou atmosféru, tak lidstvo vyhyne.

 

Pro šťoury a scifisty upřesním: Tato implikace je pravdivá z pohledu naší doby. Shodneme se potom, že je tato implikace pravdivá? Snad ano.

 

Pokročilá poznámka: Tím omezením na naši dobu nic nekazíme. Pravdivost či nepravdivost se v logice vždy děje v rámci nějakého světa, logika nepředpokládá existenci absolutních pravd. Důležité je mít konzistentní svět a v průběhu úvahy jej neměnit. Zájemci si mohou v nějaké pěkné učebnici logiky nalistovat kapitolku o ohodnocení, případně o interpretacích.

 

K čemu taková implikace je? V zásadě je to nástroj, jak se dozvědět něco, k čemu nemáme přímý přístup. Představme si, že jsme emzáci a potřebujme vědět, zda lidstvo ještě funguje, ale jsme daleko. Pokud zjistíme, že Země nemá atmosféru (což se asi dá zjistit z dálky lépe, než existence lidí), pak podle platné implikace (I ) už jistě víme bez dalšího zkoumání, že je po lidech.

 

Toto použití je typické a přirozené, přesně tohle nám ta věta vlastně říká. Tento trik, že namísto podmínky obtížně rozhodnutelné se vyzkouší nějaká jiná, pokud možno lehčí, se často používá zejména v matematice. Obecně se popsaná úvaha dá vyjádřit následujícím schématem.

 

• Dáno: implikace p => q platí.
• Dáno: p platí.
• Závěr: q platí.

 

Možná jste se s podobnými obrázky už setkali. Takto si správné úvahy připomínali ve středověku, když ještě neměli náš pohodlný systém formální logiky. Toto se jmenuje modus ponens (ale o středověké logice by měl spíš psát někdo jiný, kdo o tom něco ví, tak toho rychle nechám).

 

V situaci, kdy máme pravdivou implikaci, tak znalost o pravdivosti p postačuje k závěru o pravdivosti q. Formálně říkáme, že "p je postačující podmínkou pro q." Je to rovnocenné vyjádření implikace, takže namísto implikace "Když někomu usekneme hlavu, tak umře" je možné říct, že "useknutí hlavy je postačující podmínka pro smrt," a bude to totéž (i z hlediska formální logiky).

 

Mimochodem, pořád mluvíme o pravdivých implikacích, protože ty nepravdivé jsou coby nástroj k ničemu. Často se ale při analýze důvodů, proč určitá implikace neplatí, dozvíme docela zajímavé věci. Zvědavé čtenáře odkazujeme na již inzerovaný bonus na konci.

 

Bohužel je i pravdivá implikace nástroj značně nespolehlivý. Představme si následující situaci. Potřebujeme vědět něco o podmínce q, ale moc se nám to nedaří, tak se to pokusíme oblafnout pomocí pravdivé implikace p => q. Podíváme se na podmínku p a zjistíme, že neplatí. V takovém případě nevíme o q pořád nic, implikace nám nepomůže. Všimněte si, že jsme platnost implikace definovali pouze na základě toho, co se děje v případě splnění předpokladu. Její pravdivost tedy neovlivní, co se stane v případě, že předpoklad splněn není; jinými slovy, ani pravdivá implikace se k této situaci nemůže vyjádřit. To znamená, že pokud naše úvaha začne "implikace p => q platí" a "p neplatí," tak už jsme skončili, zde žádný diagram správné úvahy nemáme. Je to ostatně pěkně vidět na našem příkladě, pravdivé implikaci (I ). Pokud není splněn její předpoklad, tak je na Zemi atmosféra, ale o existenci lidstva to neříká nic (způsobů vyhynutí si umíme určitě představit víc).

 

Toto je jedna ze základních vlastností implikace a je to zároveň jeden z případů, kdy se "lidový" pohled na logiku neshoduje zcela s formálním, viz kapitolka o "běžné" řeči.

 

Další důležitou vlastností implikace je, že se obecně nedá obrátit. Pokud se dozvím, že u pravdivé implikace "p => q" je splněn závěr q, pak mi to neříká nic o platnosti předpokladu p. Neplatí tedy nutně, že z pravdivosti q vyplývá pravdivost p, jinými slovy, implikace "q => p" nemusí být pravdivá. Někdy pravdivá je (když máme štěstí), pak jsme vlastně v situaci ekvivalence, viz níže. Obecně se na to ale spoléhat nemůžeme, pravdivosti výroků p => q a q => p spolu vůbec nesouvisejí. Například u naší platné implikace (I ) vidíme, že jejím obrácením (konverzí) získáme tuto implikaci:

 

Jestliže lidstvo vyhynulo, pak Země musela ztratit atmosféru.

 

Protože jsou možné i jiné způsoby vyhynutí než ztráta atmosféry, je tato implikace nepravdivá. Z praktického pohledu je tedy implikace jednosměrná, což se právě projevuje tím, že je to nespolehlivý nástroj. Jednu zajímavou věc ale udělat lze.

 

Představme si, že máme pravdivou implikaci "p => q" a dozvíme se, že závěr q neplatí. Pak nemůže platit ani p, protože kdyby p platilo, tak by si vynutilo platnost q. Vidíme tedy, že když máme pravdivou implikaci "p => q," tak automaticky platí i implikace "ne q => ne p" zvaná obměna (popř. obměněná implikace).

 

Jak to vypadá u našeho příkladu? Z platné implikace (I ) vznikne rovněž platná obměna, implikace:

 

Jestliže lidstvo žije, pak musí mít Země atmosféru.

 

Zdá se, že to funguje, i na tomhle bychom se snad shodli.

 

I k této úvaze si uděláme diagram (druhý a poslední, nic dalšího s implikací dělat nejde).

 

• Dáno: implikace p => q platí.
• Dáno: q neplatí.
• Závěr: p neplatí.

 

Zkusme se na tuto situaci podívat z pohledu člověka, který se snaží o splnění p. Vidíme, že jestliže chceme mít alespoň nějakou naději, že p platí, pak k tomu nutně potřebujeme vědět, že platí q, bez toho jsme bez šance. Formálně říkáme, že "q je nutná podmínka pro p." (Ale není postačující, o tom už jsme mluvili). Zase jde o rovnocenné vyjádření ekvivalence, například namísto implikace "Když někdo žije, tak někdy žili jeho rodiče" je možné říct, že "existence jeho rodičů je nutná podmínka pro existenci dotyčného člověka."

 

Abychom to shrnuli, implikace "p => q" se dá rovnocenně vyjádřit slovy, že "p je postačující podmínka pro q", popřípadě že "q je nutná podmínka pro p". Přesně logicky řečeno, tyto tři výroky mají vždy nutně stejnou pravdivost, buď všechny platí nebo všechny neplatí. Zkusme si to na příkladě. Mám-li pravdivou implikaci, třeba "Jestliže jsem se dožil svých dvacetin, pak jsem se dožil i svých desátých narozenin," pak musí být nutně pravdivá i tvrzení "mé dožití se dvacetin postačuje k tvrzení, že jsem se dožil desetin" a "dožit se desíti je nutné pro dožití se dvacetin" (a naopak z jejich pravdivosti vyplývá pravdivost původní implikace). Na druhou stranu následující tři výroky jsou všechny nepravdivé: "Jestliže obědvám, tak v San Franciscu prší", "mé obědvání postačuje k tomu, aby v San Franciscu pršelo" a "déšť v San Franciscu je nutný pro to, abych obědval".

 

Poznámka pro humoristy: Říkali jsme si, že když je v implikaci nepravdivý předpoklad, tak je implikace automaticky pravdivá bez ohledu na závěr. Dají se tak vytvářet zaručeně pravdivé implikace: "Jestliže 2 + 2 = 5, pak jsou na Marsu malí zelení mužíčci." Z takových implikací ale moc užitku není, takže nás zajímají spíš ty implikace, kde je předpoklad alespoň někdy splněn.

 

 

Ekvivalence
Bavili jsme se o tom, že pravdivá implikace p => q je jako nástroj nespolehlivá v tom smyslu, že když místo podmínky q zkoumáme podmínku p, tak nám to pomůže jen někdy, když ta p vyjde pravdivá. Bylo by mnohem lepší, kdyby to spojení bylo oboustranné. Takové spojení nám nabízí ekvivalence, spojení dvou výroků tímto způsobem značíme "p <=> q." Taková ekvivalence je pravdivá, jestliže je vždy pravdivost výroků p a q stejná. Z toho hned vidíme, že ekvivalence je již z podstaty symetrická, p a q v ní hrají stejnou roli. Tradičně říkáme "p tehdy a jen tehdy, když q," případně "p přesně tehdy, když q", ale jsou i jiná vyjádření, třeba "p a q jsou ekvivalentní".

 

Jestliže je u pravdivé ekvivalence platnost těch dvou výroků nutně stejná, tak to znamená následující:

 

• Pokud platí p, musí platit i q.
• Pokud platí q, musí platit i p.
• Pokud neplatí q, neplatí ani p.
• Pokud neplatí p, neplatí ani q.

ˇ

 

První dva řádky říkají, že ekvivalence v sobě zahrnuje implikace jdoucí oběma směry, což nám to značení pěkně naznačuje. Je to ale i naopak. Pokud máme pravdivé implikace oběma směry, tj. první dvě tvrzení výše, pak máme automaticky i jejich obměny, což jsou ta druhá dvě tvrzení, čili platí všechny čtyři a výroky p a q musí mít stejnou pravdivostní hodnotu. Dostáváme pak tedy pravdivou ekvivalenci. Formálně říkáme, že p <=> q právě tehdy, když p => q a q => p. Tak se také platnost ekvivalence v praxi většinou dokazuje, ukáže se platnost implikace v obou směrech.

 

Zkusme si vymyslet nějakou pravdivou ekvivalenci:

 

Mám v peněžence pětikorunu, ještě jednu pětikorunu a dvě desetikoruny tehdy a jen tehdy, když tam mám dvě pětikoruny, desetikorunu a ještě jednu desetikorunu.

 

Tento příklad myslím krásně vyjadřuje symetrii ekvivalence, stejně tak bychom totiž mohli ty dva základní výroky prohodit a říct toto:

 

Mám v peněžence pětikorunu, ještě jednu pětikorunu a dvě desetikoruny tehdy a jen tehdy, když tam mám dvě pětikoruny, desetikorunu a ještě jednu desetikorunu.

 

Z hlediska faktického jsou obě ekvivalence stejné, rovněž formální logika v nich nevidí rozdíl.

 

Protože ekvivalence zahrnuje implikace oběma směry, tak vlastně dostáváme, že u pravdivé ekvivalence p <=> q představuje p podmínku nutnou a postačující pro q a zároveň je q nutná a postačující podmínka pro p. Z pohledu praktického je taková ekvivalence výrazně užitečnější než implikace, protože nemá její hlavní nevýhodu (jednosměrnost a z ní plynoucí nespolehlivost). Můžeme se tedy rozhodnout, kterou z částí budeme zkoumat (p nebo q), a cokoliv se dozvíme, platí i pro tu druhou. Jsou ekvivalence, u kterých to takto funguje a jsme za to rádi.

 

Často je ale situace trochu odlišná od chladné logiky v tom, že pro nás ty podmínky nejsou z lidského pohledu rovnocenné, jednu část považujeme za důležitější (to je to, co opravdu chceme vědět, většinou je těžší) a druhá část je testovací, pomocí ní se rozhodujeme. Jazykové vyjádření (p přesně tehdy, když...) naznačuje, že se dozvídáme něco o p, přičemž jako zdroj informace slouží q (je tedy testovací podmínkou). To nám ekvivalence umožňuje, když se podíváte na ta čtyři tvrzení výše, tak mimo jiné vidíte, že se pravda i nepravda přenáší z q na p.

 

To ovšem neznamená, že by symetrie nebyla, pořád tam je, jen se prostě jeden směr pohledu v nějakém konkrétním případě nevyužije (ale kdyby byl třeba, je k dispozici, konec konců, výroky se dají vždycky prohodit a říct "q přesně tehdy, když...", pak už je to i jazykově naopak). To je přímo zabudováno do popisované situace, jakmile se totiž jedním směrem přenáší pravda i nepravda, pak už automaticky funguje i ten druhý směr a dostáváme situaci symetrickou. Formálně řečeno, jestliže platí implikace "q => p" a "ne q => ne p", pak už nutně musí platit i implikace k nim opačné a dostáváme zase ty čtyři výroky výše čili symetrickou ekvivalenci.

 

Snažil jsem se matematice vyhnout, ale přeci jen si neodpustím jednu malou exkurzi, protože v zásadě nevyžaduje znalost matematiky. Existuje objekt zvaný řada (nekonečný součet), a řada buď konverguje (nekonečné sčítání se kupodivu nasčítá do konečné sumy), nebo diverguje. Bohužel se to strašně špatně zjišťuje. Pokud si čtenář otevře v zásadě libovolnou učebnici analýzy na kapitole o řadách, tak tam najde spoustu implikací, které představují testy konvergence či divergence. Mají shodný obecný tvar: Jestliže je splněna nějaká podmínka, tak řada konverguje (popř. diverguje). Jde tedy o postačující podmínky. Člověk dostane řadu, tak vyzkouší nějakou podmínku. Pokud není splněna, tak se neví nic (je jen postačující, implikace vede jen jedním směrem), musí se zkusit jiná. Při troše štěstí se ale dřív či později povede, že nějaká podmínka splněna bude, a pak už se ví, jak je na tom dotyčná řada s konvergencí. Hned někde na začátku kapitoly by se ale také měla objevit implikace zvaná "nutná podmínka konvergence." V praxi to funguje tak, že když má člověk podezření, že daná řada nekonverguje, tak zkusí nutnou podmínku konvergence. Pokud vyjde, tak se vlastně neví nic (z platnosti nutné podmínky nic neplyne). Pokud ale nutná podmínka konvergence selže, tak už příslušná řada zaručeně nekonverguje. Většinou se tam najde také jedna ekvivalence, u limitního srovnávacího kritéria. To říká, že v případě, kdy jsou si dvě řady "podobné", jedna konverguje přesně tehdy, když konverguje ta druhá. Tento test je velice oblíbený, komplikovaná zadaná řada se nahradí jednodušší (ale "podobnou") řadou testovací. U té prozkoumáme konvergenci a cokoliv vyjde, nutně už platí i pro řadu danou. Vidíme tedy, že implikace a různé pohledy na ni nejsou jen akademickými hrátkami, ale docela praktická věc.

 

Na začátku jsme si říkali, že logika nepotřebuje nějaké absolutní pravdy. Ona také žádné pravdy neposkytuje pro oblasti mimo sebe. Tím míním, že je samozřejmě například pravda, že implikace "p => q" a "ne q => ne p" mají vždy stejnou pravdivost, ale to je pravda zajímavá z hlediska logiky. Takových nám nabízí hodně, ale žádná z nich nám sama o sobě příliš nepomůže při zkoumání světa kolem. Hlavním praktickým přínosem logiky je "posouvání" pravdy z jednoho místa na jiné, jak jsme ostatně viděli výše. Když tedy logiku používáme například v přírodních vědách, tak slouží jen jako kontrola, že do našich úvah nevnášíme chyby, ale nedokáže vytvořit něco z ničeho. Příslušný vědecký obor sám musí na začátku přijít s věcmi, které jsou považovány za pravdivé ("fakta"), a logika pak může ospravedlnit proces, kterým se z nich došlo k jiným faktům. Jinými slovy, spolehlivost nějaké logické úvahy je dána spolehlivostí vstupních údajů. Jakmile je v nich nějaká chyba, logika už to nezachrání (maximálně na tu chybu při troše štěstí upozorní, pokud se nějaká vstupní data dostanou navzájem do sporu).

 

 

Logika a "běžný" jazyk
Zajímavou otázkou je vztah "normálního života" a logiky, lidé relativně často mluví o tom, že něco je či není logické. To je problématické zejména v situaci, kdy se řeší, co kdo řekl, protože normální člověk samozřejmě není v logice vzdělán a tudíž není důvodu předpokládat, že se bude vyjadřovat vždy formálně správně. "Lidská logika" a "formální logika" se nejčastěji neshodnou ve dvou situacích.

 

Tou první je implikace, lidé ji totiž často řeknou jako implikaci, ale ve skutečnosti ji chápou jako ekvivalenci. Pro případ není třeba chodit daleko, asi každý z nás zaslechl větu typu "Když budeš hodný, dostaneš čokoládu." Zlobivému potomku pak bývá na její konto čokoláda upírána. Pokud by ovšem dotyčný zlobivec znal logiku, prohlásil by: "Drahý rodiči, tvůj výrok byl implikace. Dal jsem si tu práci, abych udělal její předpoklad nepravdivým, takže ať už mi teď čokoládu dáš nebo nedáš, ona zůstane pravdivou. Můžeš mi tedy čokoládu dát a své slovo neporušíš." Zaplať pánbůh, že se děti učí formální logiku až v pubertě, když už na tom, co rodiče říkají, stejně moc nezáleží.

 

Fikaný rodič by samozřejmě řekl: "Když budeš zlobit, nedostaneš čokoládu." Všimněte si, že tím zároveň nic neslibuje pro případ, že by dítě bylo hodné! Přiznám se ale, že mi takovéto zneužití logiky proti vlastním dětem přijde nefér, navíc by psychologové namítli, že je vhodnější mluvit o odměnách než o trestech. Nárokům formální logiky i psychologie vyhovuje věta "Čokoládu dostaneš tehdy a jen tehdy, když budeš hodný," ale ještě jsem nepoznal rodiče, kterým by se do toho chtělo (a to znám i rodiny, kde jsou oba rodiče matematici).

 

Je ještě jeden rozdíl mezi logikou a běžným životem. Jak už jsme psali, implikace "Jestliže 2 + 2 = 5, pak jsou na Marsu malí zelení mužíčci" je z pohledu logiky zcela korektní pravdivá implikace, ale z hlediska běžné řeči je to nesmysl. Narážíme tím na rozdíl mezi logickými implikacemi, které se nezajímají o obsah řečeného, jen o pravdivost/nepravdivost základních výroků, a implikacemi "ze života" (materiálními), kdy se očekává nějaká reálná souvislost mezi zmiňovanými jevy. I tento rozdíl přispívá k občasnému nedorozumění mezi formální logikou a hovorovým jazykem.

 

Druhá zmatečná situace vzniká tím, že jsou vlastně dvě spojky "nebo". Jedna funguje tak, že je "p nebo q" splněno, pokud platí alespoň jedna z těch dvou podmínek, což ale umožňuje i platnost obou. To je to "pravé" logické nebo, příkladem budiž třeba podmínka "3 roky nebo najetých 30,000" pro propadnutí záruky na auto. Je zjevné, že pokud jsou splněny obě části, tak záruka stále padá neboli výrok je považován za pravdivý.

 

To druhé nebo je "vylučovací nebo", logické "xor", které se správně říká "buď-nebo". Výrok "p xor q" je pravdivý v případě, že platí právě jeden z výroků p či q. Pokud by platily oba, je "p xor q" nepravdivé. "V tomhle bytě budu buď já, nebo tvá sbírka hadů." Problém je, že lidé jsou od přírody líní a ne vždy to "buď" říkají, takže není vždy jasné, jaké "nebo" vlastně myslí. Klasickým příkladem budiž výzva "Peníze nebo život." To je evidentně myšleno jako "xor", je to vlastně slib, že když se rozhodnete učinit pravdivou tu část o penězích, bude už část o životě nutně nepravdivá. (Ono to nakonec možná ani nebude "nebo", řekl bych dokonce, že to ten lupič myslel jako implikaci.)

 

Když si k tomu přičteme, že lidé sami kolikrát ve chvíli, kdy něco říkají, ani pořádně neví, jak to myslí, jsou pokusy o logickou analýzu běžné řeči dost náročným úkolem, který asi nebude nikdy zcela splnitelný. Nemám ale pocit, že by to nějak zvlášť vadilo, ještě jsem neslyšel, že by se štamgasti v hospodě dožadovali odborníka na logku, ať je rozsoudí. Naopak mnohým lidem to zjevně vysoce vyhovuje, nejsme jedinou zemí, kde lidé spekulují, jestli postupné změny ve vzdělávání, zejména odklon od precizního myšlení k tvůrčímu plkání, není od politiků záměrem.

 

Tyto problémy zcela přirozeně odpadají tam, kde je logika opravdu používána, tedy ve vědě. Vědec většinou ví, co chce říct, své články si pečlivě promýšlí, aby říkaly přesně to, co mají, navíc píše češtinou odbornou, která je formálnější a nutí vědce k přesnějšímu vyjadřování.

 

Je ještě jeden důvod, proč aplikace logiky na život není závratně úspěšná. Síla logiky je v její přesnosti, ale právě ona omezuje oblast jejího působení, ne všechno v životě je 0 nebo 1. Tím se třeba vysvětlí, proč sice už nějakých 60 let existuje Godelův "důkaz existence Boha," ale pořád se najdou matematici a logici, kteří v Něj nevěří. Důkaz má totiž z hlediska našeho skutečného světa několik podstatných děr.

 

Existují pokusy se nějak odpoutat od oné někdy nepříjemné přesnosti logiky, například je tu relativně nová disciplína zvaná fuzzy logika, která namísto pravdy-nepravdy pracuje se spolehlivostí informace. Jestliže máme implikaci, která je spolehlivá v 90 procentech případů, a její předpoklad je splněn v 70 procentech, co se dá říct o platnosti závěru? (Zde samozřejmě zjednodušuji, pracuje se s rozděleními pravděpodobnosti, ostatně na podobném základě funguje kvantová mechanika a není to náhoda.) Ale to už odbočuji, navíc v této oblasti nepracuji, takže bych to raději nechal povolanějším.

 

Ona výhoda a nevýhoda přesnosti je mimochodem ještě výrazněji vidět u matematiky, která je asi nejmocnějším nástrojem ke spolehlivému poznávání světa kolem nás, ale právě ta přesnost už z principu znemožňuje její použití v mnoha zajímavých oblastech. A je to dobře, naštěstí jsou ještě na světě věci, které nelze spočítat.

 

 

Bonus: Jedna implikace z matematiky
Zde si zkusíme rozebrat jednu klasickou implikaci. Předpokládám, že čtenář článku už někdy nějakou funkci potkal, takže má představu, co to je, mnozí už si dokonce nějakou funkci i zderivovali. Ale abychom srovnali startovní pole, zkusím teď neformálně představit dva důležité pojmy používané u funkcí. Protože zde bude podstatná spíš ta implikace než matematika, nebudu zcela přesný, ale vadit to může maximálně matematikům a ti tohle stejně číst nemusí.

 

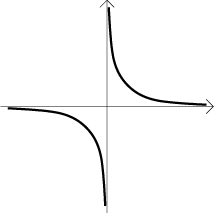
 Řekneme, že daná funkce je spojitá, jestliže její graf můžeme nakreslit nepřerušovanou čárou, přičemž je ale povoleno přerušení v místech, kde funkce vůbec neexistuje. Například funkce f(x) = 1/x je spojitá, protože má graf přerušen jen v jediném místě, pro x = 0, ale tam je to nutné už z principu, protože v nule ta funkce vůbec neexistuje (viz obrázek). Typickou spojitou funkci si tedy představíme jako jeden či několik nepřerušovaných úseků grafu, s tím, že mezi úseky funkce vůbec neexistuje. (Poznámka pro šťouraly: Uvažujeme tedy jen funkce, jejichž definiční obory se sestávají z nedegenerovaných intervalů.)

 

Existuje proces zvaný derivace, kdy se z jedné funkce vyrobí funkce jiná. V praxi se to většinou dělá jednoduchým algoritmem, který se poštve na daný vzorec a vyleze z toho vzorec jiný, ale není to vždy nutně takto. Řekneme, že funkce je diferencovatelná, pokud se dá zderivovat všude, kde existuje. (Poznámka pro pokročilé šťouraly: Kde je to nutné, uvažujeme jednostranné derivace.)

 

Jedna ze základních vět analýzy říká následující:

 

Jestliže je daná funkce diferencovatelná, tak je spojitá.

 

Jde tedy o jasnou implikaci, která mimo jiné říká, že diferencovatelnost je postačující podmínka pro spojitost. Každá diferencovatelná funkce je i spojitá. Jinak řečeno, v hierarchii vlastností stojí diferencovatelnost nad spojitostí (nebo jsou na stejné úrovni, to ještě není jasné). Toto se používá v některých teoretických úvahách, kdy na začátku máme informaci o diferencovatelnosti, ale později začne být důležitá i spojitost. Díky této implikaci ji automaticky máme.

 

 

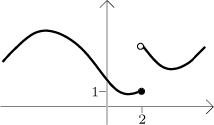
 Víme, že to zároveň znamená, že spojitost je nutná pro diferencovatelnost. To nám umožní snadno odpovědět na otázku, jestli jdou derivovat všechny funkce. Odpověď zní, že ne, stačí vzít nějakou nespojitou funkci a dostaneme také funkci, která není diferencovatelná. Funkce napravo není spojitá, protože je její graf přetržený v bodě x = 2, nejde přitom o přetržení "nutné": Funkce v tom bodě v pohodě existuje, má hodnotu 1. Podle naší implikace pak tuto funkci také nelze alespoň někde derivovat, není asi překvapením, že se derivování pokazí zrovna v té dvojce.

 

 

 Vyrábět funkce bez derivace tímto způsobem je ale příliš jednoduché. Zajímavější příklady dostaneme, když se zeptáme, jestli ta implikace náhodou není ekvivalence. Mohlo by být pravda, že ze spojitosti již plyne diferencovatelnost? Ukáže se, že ne. Máme tedy příklad neplatné implikace "jestliže spojitá, pak diferencovatelná", což je zajímavá situace, protože bychom rádi věděli, za jakých okolností tato implikace selhává. Jak vypadá spojitá funkce, kterou nejde derivovat? Nejprofláklejším příkladem je absolutní hodnota, jejíž graf je vidět vlevo. Je spojitá, ale dá se ukázat, že v počátku nejde derivovat. Hloubější analýza ukáže, že za to může ten ostrý zlom.

 

 

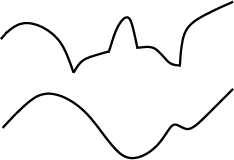
Díky zamyšlení nad pravdivou i nepravdivou implikací jsme tak dospěli k dobrému intuitivnímu pocitu, co ty dva pojmy znamenají. Spojitá funkce má nepřerušovaný graf, zatímco diferencovatelná funkce má nepřerušovaný graf, který navíc musí zatáčet povlovně, nesmí mít na sobě žádné ostré zlomy. Na obrázku je první funkce jen spojitá, druhá i diferencovatelná.

 

Poznámka: Pokročilejší čtenáře možná napadne, proč jsem nepracoval s lokálními pojmy, jmenovitě s krásnou (a pravdivou) implikací

 

Jestliže je funkce v nějakém bodě diferencovatelná, pak je tam i spojitá.

 

Je pravda, že bych to pak měl v mnoha směrech jednodušší, ale vznikl by jiný problém. Bodové vlastnosti se nedají tak pěkně laicky popsat. To, že je nějaká funkce spojitá či dokonce diferencovatelná v nějakém bodě, totiž vůbec nemusí znamenat, že je někde souvislá. Jsou příšerky, které diferencovatelnost někde mají, ale jejich grafy nemají vůbec žádné souvislé úseky! Takže jsem raději volil variantu s menšími podvůdky, ale pěknějšími obrázky.