Známky nové částice se však mohou v procesech pozorovaných na urychlovači projevit i tehdy, když nemá dostatečnou energii k jejich reálné produkci. Kvantová fyzika a její Heisenbergův princip neurčitosti umožňují realizaci různých procesů prostřednictvím vzniku a opětné přeměny i velmi hmotné částice. Lze to interpretovat tak, že díky Heisenbergovu principu neurčitosti se na velmi krátkou dobu může narušit zákon zachování energie. Pokud je součin doby existence tohoto narušení a velikosti této energie menší než hodnota daná právě Heisenbergovým principem neurčitosti, není toto narušení pozorovatelné a neodporuje zákonu zachování energie. V tomto případě mluvíme o virtuální existenci dané částice.

 

První věc, kterou je třeba si uvědomit, že vztah mezi neurčitostí energie a časem není skutečná Heisenbergova relace neurčitosti, tak jako například vztah mezi neurčitostí polohy a hybnosti, protože čas není v kvantové teorii pozorovatelná veličina, ale parametr. Neexistuje žádný konzistentně definovaný operátor času. Ale to nechme stranou a ptejme se, co relace mezi neurčitostí energie ΔE a neurčitostí času Δt

ΔE Δt ≥ h/4Pi

(kde h je Planckova konstanta) znamená. V žádném případě to neznamená, že například během srážky dvou protonů na LHC „se na velmi krátkou dobu může narušit zákon zachování energie.“. To prostě není pravda. Energie systému, jeho dynamika je řízena Hamiltoniánem nezávisícím na čase, se striktně zachovává po celou dobu jeho existence. Uvedená relace říká, že chceme-li tuto energii znát s přesností ΔE, musí systém existovat po dobu aspoň Δt. Vezmeme-li například nestabilní částici, která nemá dobře definovanou hmotnost m (a tedy ani klidovou energii E=mc²), pak střední doba jejího života τ je svázána s její pološířkou energie Γ právě vztahem  Γt  ≥ h/4Pi. Například Higgsův boson má hmotnost 125,11 GeV, jeho doba života je cca deseti tisícina atosekundy (tj.10^-22 s) a pološířka činí cca 0,004 GeV. Pokud by měla být neurčitost energie kolem 400 GeV, což je spodní hranice na hmotnost hypotetických nových částic, musela by být doba života Higgsova bosonu sto tisíckrát kratší, tedy miliardtina atosekundy (tj. 10^-27 s). Doba života svazků protonů na LHC je přitom typicky 10 hodin a relativní neurčitost energie 1 promile, tedy při srážkové energii 14 TeV jen 14 GeV. Přitom neurčitost energie způsobená konečnou dobou, po níž je energie protonu před srážkou měřena, je zcela zanedbatelná.

Vladimírova interpretace pojmu virtuální částice je chybná, protože předpokládá, že ve srážkách reálných částic, například dvou protonů na urychlovači LHC v CERN, vznikají na krátký čas velmi hmotné reálné částice, tedy částice jejich energie E a hybnost p splňují podmínku

E² = p² c² + m² c⁴ kde m je hmotnost této částice (někdy se říká, že jsou „na hmotové slupce“), „které narušují zákon zachování energie“. To ale není pravda a v intermediálních stavech srážek vznikají stavy jednotlivých kvantovaných polí, které je zvykem, ale ne nutností, nazývat virtuální částice, které nesou energii, hybnost, spin a vnitřní kvantová čísla podobně jako reálné částice, ale pro něž výše uvedený vztah neplatí. Ty jsou ve výrazech pro fyzikální veličiny representovány tzv. propagátory příslušných částic. Pojem virtuální částice není ve skutečnosti třeba vůbec zavádět a vystačíme jen s propagátory.

 

Nejjednodušším příkladem je Feynmanův levý diagram na obrázku vlevo popisující rozptyl dvou elektronů v nejnižším řádu poruchové kvantové elektrodynamiky. Elektrony na sebe působí tím, že si „vyměňují“ virtuální foton, kvantum elektromagnetického pole. Elektrony před rozptylem i po rozptylu jsou reálné elektrony, pro něž platí vztah E² = p² c² + m² c⁴, zatímco foton, který jako reálná částice má nulovou hmotnost, a tedy pro něhož platí E² - p² c² = 0 , je virtuální, neboť pro něj platí E² - p² c² < 0. Virtuální částice ovšem mohou vystupovat i ve složitějších Feynmanových diagramech s uzavřenými smyčkami, jako je tomu na diagramu vpravo, kde se virtuální foton přemění na pár virtuálního elektronu a virtuálního pozitronu nebo na jakoukoliv dvojici nabitých částic a antičástic. Ve všech vrcholech se přitom striktně zachovává energie a hybnost. Příspěvek jednotlivé virtuální částice, která nese energii E a hybnost p, do daného procesu, tedy její propagátor, je přitom nepřímo úměrný její virtualitě ν = E² - p² c²- m² c⁴. To se obvykle vyjadřuje slovy, že čím je její virtualita bližší nule, tím virtuální částice „žijí“ déle a svým chování se blíží reálným částicím, pro něž ν = 0. Naopak, čím je virtualita větší, tím menší je příspěvek virtuální částice do daného procesu. Ve vnitřních linkách, odpovídajících virtuálním částicím, se přitom mohou vyskytovat i virtuální částice, které jako reálné částice mají tak velkou hmotnost, že na jejich produkci v koncovém stavu nestačí energie srážky. Takto definovaný pojem virtuální částice je ovšem něco jiného než výraz „virtuální existence částice“, který navádí představu, že se na chvilku rodí reálná částice, zatímco virtuální částice není reálná částice. Vladimír Wagner dále píše

Možnost průběhu reakce i prostřednictvím virtuální částice, která má klidovou energii překračující hodnotu energie zúčastněné v procesu, ovlivňuje jeho pravděpodobnost. Může třeba zvýšit pravděpodobnost rozpadu nějaké částice a snížit její dobu života.

Výraz „klidová energie virtuální částice“ nemá smysl, protože klidový systém virtuální částice neexistuje. Klidová energie reálné částice není nic jiného než její hmotnost (násobená kvadrátem rychlosti světa). Wagnerův argument se zjevně opírá o představu, že i velmi těžké částice v intermediálním stavu srážek částic mají energii minimálně rovnou jejich hmotnosti. To ale pro virtuální částice neplatí. Jejich energie jsou vždy a přesně v souladu se zachováním celkové energie srážky. Výraz „virtuální částice, která má klidovou energii překračující hodnotu energie zúčastněné v procesu“ nelze číst jinak než jako tvrzení, že na chvilku se nezachovává celková energie srážejících se částic. Nic takového ale kvantová teorie pole nepřipouští.

Jak jsem již uvedl, těžké částice, které nelze ve srážkách vyprodukovat, protože celková srážková energie je nedostatečná, mohou stejně jako lehké částice existovat v intermediálních stavech jako virtuální částice a tím samozřejmě ovlivňují pravděpodobnost fyzikálních jevů. Jako jednoduchý příklad vlivu těžkých částic na pravděpodobnost nějakého procesu nebo vlastnost částice můžeme vzít vliv hypotetické částice zvané leptokvark na vlastnosti mionu, které by se projevily například v hodnotě jeho anomálního magnetického momentu.

 

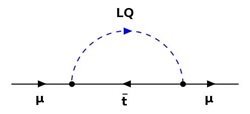
Na obrázku se počáteční mion na chvilku přemění na pár virtuálního t-kvarku a virtuálního leptokvarku LQ s velkou hmotností, který se rychle spojí zpět do fyzikálního mionu. Součet energií virtuálního t-kvarku a virtuálního leptokvarku je přitom přesně roven energie počátečního mionu.

 

Důvod, proč je příspěvek tohoto diagramu malý, spočívá v tom, že typická virtualita těžkého leptokvarku v tomto diagramu je velká, tj. leptokvark je daleko od hmotové slupky a jeho příspěvek do anomálního magnetického momentu mionu, daný jeho propagátorem, je nepřímo úměrný této velké virtualitě a je proto malý. Ani slovo o Heisenbergově relaci neurčitosti a nezachování energie.

 

Jeden z hlavních výsledků konference, byť v jistém smyslu negativní, byl právě výsledek nejnovějšího výpočtu anomálního magnetického momentu mionu, který je v dobrém souhlasu s měřeními ve Fermilab, ale v rozporu s jinými výpočty, které naznačovaly rozpor se Standardním modelem a možnou existenci nových částic, jako je například uvedený leptokvark.

 

Této práci a anomálnímu magnetickému momentu mionu je věnován další Wagnerova rozsáhlá zpráva z konference ICHEP 2024 příznačně nazvaná Tak nám zmizel nejjasnější signál exotické fyziky, která končí závěrem

 

Nové zpřesněné výpočty postavené na Standardním modelu hmoty a interakcí umožnily spočítat hodnotu magnetického dipólového momentu mionu. Nová teoretická hodnota je ve velmi dobré shodě s experimentální hodnotou potvrzenou a zpřesněnou před třemi lety ve Fermilabu.

 

To je poněkud zkreslující interpretace obsahu citované práce, která je založena na výpočtech jednoho z mnoha příspěvků do anomálního magnetického momentu mionu, tzv. hadronové vakuové polarizace, v rámci kvantové chromodynamiky na mřížce. Práce konstatuje pouze to, že jejich nejnovější výpočet využívající obrovskou a jemnou mřížku významně zpřesňuje jejich výpočet z roku 2020 a je v rámci jedné standardní odchylky v souhlasu s měřením ve Fermilab. Napětí (tension) mezi výsledky výpočtu na mřížce a alternativní metodou založenou na využití experimentálních dat však zůstává a s konečným závěrem bychom proto měli počkat až na reakci třech skupin, které tuto alternativní metodu používají. K výpočtům na mřížce je také vhodné dodat, že představují černou skříňku a neumožňují intuitivní interpretaci spočteného jednoho čísla.

V této zprávě Vladimír Wagner opakuje věcně chybné tvrzení

 

Virtuální částice, jejichž „doba existence“ je omezena Heisenbergovým principem neurčitosti, mohou mít klidovou energii (hmotnost) vyšší i řádově, než je energie v systému dostupná. Na této úrovni tak nemusí být splněn zákon zachování energie.

ale pak dodává v podstatě to, co říkám já (a nejen já, třeba i Wikipedie)

 

Lze se však na to dívat i z jiného pohledu. Definuje se, že virtuální částice není na hmotové slupce a nesplňuje rovnici E²=E₀²+p²c², kterou musí splňovat každá reálná částice. Zde je E celková energie, p hybnost a E₀ klidová energie částice daná její klidovou hmotností E₀=m₀c². V tom případě není nutné opustit splnění zákonu zachování energie a hybnosti.

 

To ale není jiný pohled, to je jediný pohled přímo odrážející způsob výpočtu fyzikálních veličin ve kvantové teorii pole. Důvod, proč považuji Vladimírovu interpretaci založenou na chvilkovém nezachování energie nejen za věcně chybnou, ale také velmi nepedagogickou, spočívá v tom, že v minulosti uvažovali i někteří významní fyzikové možnost, že se v některých jevech mikrosvěta energie skutečně nezachová. Tak tomu bylo ve snaze smířit nespojitou změnu energie atomu a spojité vyzařování elektromagnetického záření. Bohr, Kramers a Slater ještě v roce 1924 odmítali Einsteinovo kvantování energie samotného elektromagnetického záření, tedy myšlenku fotonu, a předpokládali, že v jednotlivých případech se energie během spojitého vyzařování nezachovává. Teprve výsledky Arthura Comptona s rozptylem rentgenových paprsků na elektronech, které fyzikální realitu Einsteinova fotonu definitivně prokázaly, tuto možnost pohřbily.

##seznam_reklama##

 

Podobně tomu bylo s vysvětlením spojitého spektra energií elektronů a pozitronů v beta rozpadech jader. I v tomto případě se Heisenberg a další tento fakt snažili interpretovat jako projev nezachování energie. To bylo nesnesitelné pro Wolfganga Pauliho, který ze zoufalství postuloval, že v beta rozpadech vzniká také v dnešní terminologii elektronové neutrino a energie se zachovává. Tuto hypotézu poprvé vyslovil v dopise účastníkům setkání fyziků a chemiků v Tübingen 4. 12. 1930, jehož úvodní část zní:

 

 

Vážené radioaktivní dámy, vážení radioaktivní pánové,

věnujte prosím laskavou pozornost doručiteli tohoto dopisu. Poví vám, jak jsem s ohledem na „špatnou“ statistiku jader dusíku a lithia a na existenci spojitého spektra beta rozpadů přišel na zoufalou myšlenku, jak zachránit teorém o statistice i zákon zachovaní energie. Její podstatou je předpoklad, že v jádrech existuje elektricky neutrální částice se spinem ½, která splňuje vylučovací princip a která se liší od fotonu také tím, že se nepohybuje rychlostí světla.

Postulovat existenci něčeho, co nebylo pozorováno, bylo pro Pauliho těžko stravitelné, a proto na konci dopisu znova dodává

Připouštím, že moje vysvětlení se může zdát absurdní, neboť pokud neutrony existují, měly být už dávno pozorovány. Ale jen ten, kdo si troufá, může vyhrát.

 

Pauli měl v klíčové části své hypotézy, vysvětlení spojitého spektra elektronů či pozitronů v beta rozpadech jader, pravdu, i když se ve dvou dalších předpokladech mýlil. Neutrální částice, dnešní elektronové neutrino, které Pauli nazval „neutronem“, neexistuje v jádře, ale vzniká při beta rozpadu a neřeší problém špatné statistiky jader dusíku, to vyřešil až skutečný neutron, objevený v roce 1932.

Zahrávat si s nezachováním energie je velmi nebezpečné.

 

Celý článek je zde přiložen ke stažení ve formátu docx - zde: co je virtualni castice.docx