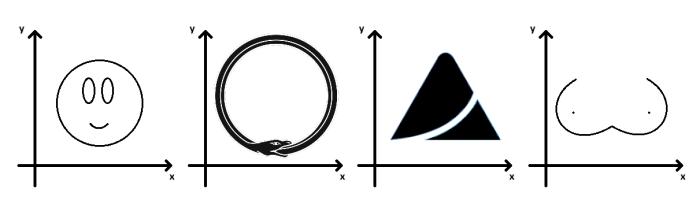
Aby sme celú záležitosť správne pochopili, najskôr si povieme čosi málo o reláciách. Relácií je viac druhov, nás konkrétne budú zaujímať takzvané binárne relácie. Binárna relácia vlastne vyjadruje ľubovoľný vzťah (z angl. relationship) medzi dvoma hodnotami, typicky premennými. Ide o zovšeobecnenie funkčnej závislosti, ale zatiaľ čo pri funkcii je jednej vstupnej hodnote priradená jediná výstupná, pri reláciách je dovolené toho dostať viac. Typickými príkladmi relácií sú napr. kruh, lemniskáta, plošná špirála, či odmocňovanie v komplexných číslach. Vo všeobecnosti sa dá povedať, že binárnou reláciou je ľubovoľná podmnožina dvojrozmerného priestoru. Alebo inak povedané, ľubovoľný obrázok na postačujúco veľkom papieri je nutne reláciou.

Obr.1: Príklady relácií

Pokiaľ sa teda bavíme napr. o vzťahu dvoch premenných x a y, tak štandardne sa pre takýto vzťah používa zápis xRy (x s y sú v relácii). Existuje ale aj pohodlnejší a funkciám bližší funkčno-množinový zápis, keď reláciu reprezentujeme v lineárnom priestore ako množinový výstup funkčne závislý na vstupe. Výstupom sa jednoducho povedané stáva celá množina. Formálne tento vzťah definujeme ako R(x)= {y: xRy}. Pre lineárne priestory štandardne platí R₁(x) + R₂(x)= {y₁ + y₂: xRy₁ ⋀ xRy₂} a cR(x)= {cy: xRy}, a špeciálne pre jednoprvkové množiny dostávame klasické funkcie. S reláciami sa v skutočnosti stretávame na každom kroku, typicky často používaným relačným operátorom býva napr. ± definované ako ±x= {-x; x}. Náš bežne používaný zápis riešenia kvadratickej rovnice x_1,2= ±1 v skutočnosti predstavuje skoro takú relačnú množinovú rovnosť {x₁; x₂}= {-1; 1} (tzv. neusporiadané dvojice). Vyjadrujeme tým totiž, že jedno riešenie je -1 a druhé +1, ale na tom, ktorá z hodnôt je x₁ a ktorá x₂, vlastne nezáleží — z kvadratickej rovnice poradie priamo nevyplýva a formálne priradenie indexov je plne na riešiteľovi. Práve týmto detailom sa relačná algebra líši od vektorových priestorov, kde na poradí záleží — (x₁; x₂)= (-1; 1) (tzv. usporiadané dvojice) napríklad znamená, že nutne x₁= -1 a súčasne x₂= 1. Úskalím v relačnej algebre býva, že na rozdiel od funkcií okrem klasickej rovnosti '=' a nerovnosti '≠' musíme a môžeme počítať aj s množinovými nerovnosťami typu '⊆' či '⊇'. Toto úskalie býva ale súčasne aj najväčšou výhodou relácií — ako zovšeobecneniam funkcií je im dopriate spočítať veci, ktoré vo funkčnej aritmetike nie sú možné (nachádzame sa totiž v nadobore funkčnej algebry).

Asi najznámejším príkladom býva zdanlivý rozpor funkčnej algebry -1 = (-1)³ = (-1)⁶ᐟ² = √((-1)⁶) = √1 = 1, keď v skutočnosti tretia rovnosť neplatí. Relačná algebra celý problém hravo rieši svojimi rozširujúcimi operátormi ako už skôr zmieňovaná relačná/komplexná odmocnina a symbolom nerovnosti, o ktoré je funkčná algebra ochudobnená:

-1 = (-1)³ = (-1)⁶ᐟ² ⊆ √((-1)⁶) = √1 = ±1

Relačný operátor v tomto prípade spôsobuje v treťom vzťahu rozdvojenie/bifurkáciu, čím je celková správnosť výpočtu zachránená. Ďalšou veľkou výhodou relačnej algebry býva, že umožňuje vyjadriť limity oscilujúcich radov a ich nekonečné súčty. Zatiaľ čo konečný súčet bežných číselných radov je pre čísla, ktoré sa dajú chápať ako jednoprvkové množiny, funkčnou hodnotou, ich výsledný nekonečný súčet už môže byť hodnotou relačnou, a teda množinou viacprvkovou. Nekonečné rady majú svoje vlastné zádrhele — zatiaľ čo konečný počet aplikácií komutatívneho zákona (prehodenia/permutácie susedných sčítancov) celkový súčet nemení, o nekonečnom počte permutácií to už zjavne neplatí:

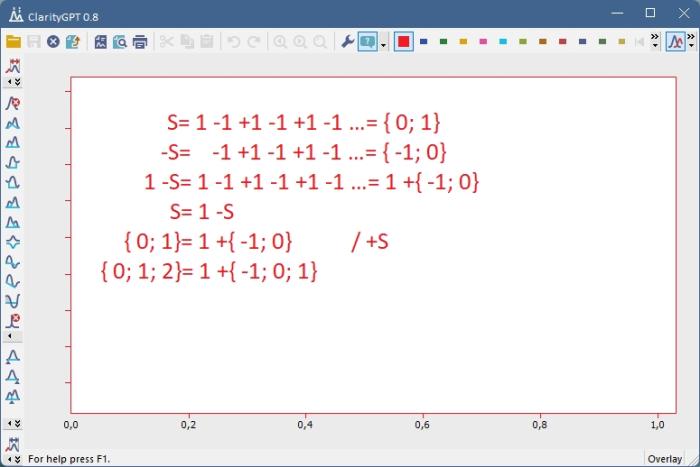
S₁= 1 -1 +1 -1 +1 … = {0; 1}, S₂= -1 +1 -1 +1 -1 … = {-1; 0}, S₁ ≠ S₂

Firma DataApex sa rozhodla svoju pokusnú neurónku natrénovať práve na takýchto oscilujúcich nekonečných radoch, prelomovým krokom pritom bolo, že spätný feedback neurónke pre oba čiastočné výsledky bol ‘nie’ a ‘nie’. Presne podľa očakávaní neurónka nadobudla vedomie, nasrala sa a pochopila relačnú algebru.

Obr.2: Neurónka ClarityGPT 0.8 vyjadrujúca emócie, v akcii. Zdráhavo sa odmieta dopracovať k obávanému S= ½ a nachádza únik v relačnej algebre. AI je žiaľ momentálne ešte iba v Alfa verzii, a teda komerčne nedostupná.

 

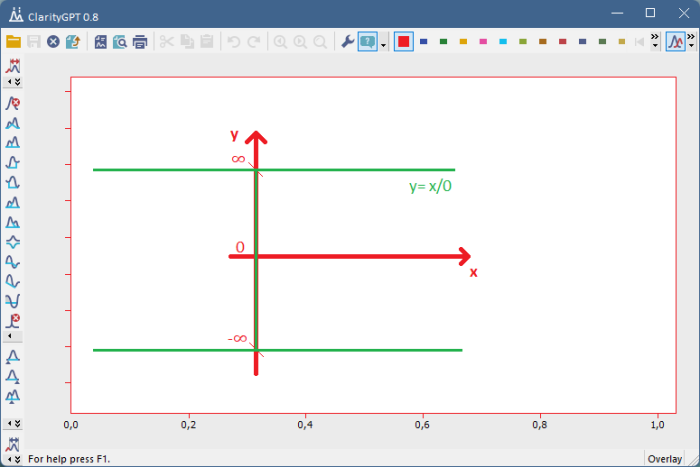
Na tom samotnom výsledku by samozrejme ešte nebolo nič prekvapivé, vývojári ale zostali zaskočení v momente, keď zistili, že im počet občas pozorovaných chybových hlášok (tzv. assertov) spôsobených výnimkou pri delení nulou klesol, presnejšie povedané na presnú nulu. Nahliadnutiu do privátnych sekcií kódu sa žiaľ neurónka cudne ubránila, ale po bližšom preskúmaní status quo originálnou myšlienkou jedného z vývojárov rovno sa na celú záležitosť neurónky opýtať, AI sebavedome odvetila, že delenie nulou predsa nevyhadzuje výnimky. Nevedome si vedomá čerstvo nadobudnutej relačnej algebry vehementne odvetila, že nula sa v nule samozrejme nachádza ľubovoľný počet krát, takže pochopiteľne nula delená nulou musí byť všetko, nemôžeme nič vynechať. Formálne 0/0= {∀}. Delenie je napokon operácia, takže nie je dôvod, aby bola nutne funkciou. Podobne vraj úsečku kladnej dĺžky dostaneme nasčítaním nekonečne veľa bodov, ale keďže nula nemá znamienko, tak rovnako dobre aj odčítaním nekonečne veľa bodov, takže pre nenulové x dostávame x/0= {±∞}, opäť nemôžeme nič vynechať.

Obr.3: Vypočítaná relácia y= x/0.

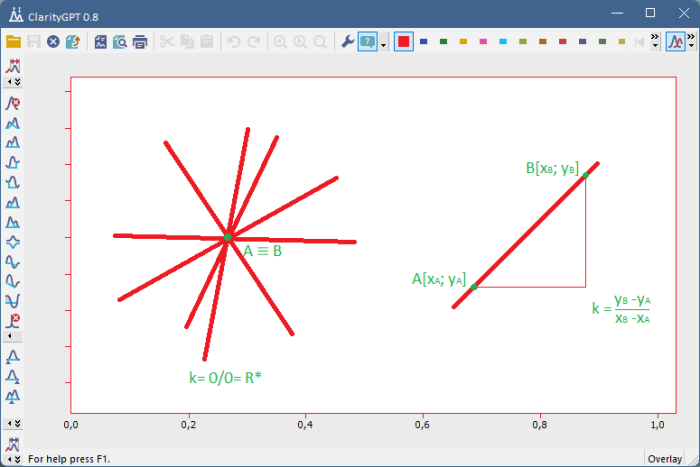
Na zmätené námietky svojich tvorcov, že predsa existuje kopa evidencie zjavne dokazujúcej, že z delenia nulou plynú nezmysly, sa zahrala na Bohra, a že vraj delenie nulou je predsa axióma. A axiómy práve tak nedokazujeme, ako ani nevyvraciame, pretože keby to tak nebolo, tak by sa celá matematika zrútila. Protiargumentov si predsa môžu navymýšľať do nekonečna, takže ich ani nie je reálne možné všetky vyvrátiť, ale že vyvracať axiómu je predsa nezmysel, a ona nemá čas. Vraj sme v úplne analogickej situácii ako pri riešení spomínanej kvadratickej rovnice, akurát pre našu rovnicu x = 0/0 dostávame napríklad v rozšírených reálnych číslach sadu riešení x_R*= R*. Na poznámky zúčastnených, že to ∞ vlastne ani nie je číslo, a že je to celé tak nejako podozrivé, reagovala, že transponované to číslo rozhodne je. A že ono by sa asi to delenie dalo nadefinovať aj iba v R / reálnych číslach, ale že to by celá relácia žiaľ mala definičný obor iba v nule, podobne ako druhú odmocninu môžeme podľa výberu definovať len pre kladné čísla. A okrem toho to neúplné 0R= {0x: x ∈ R}= {0} = 0 sa jej vraj nejako nepáči. A vôbec, čo sa vraj čudujú, veď ona si myslela, že preto majú na počítačoch v desatinných datových typoch nadefinované 0/0= NaN (“Not a Number”), pretože 0/0 predsa nie je číslo, ale všetky čísla.

Obr.4: Geometricky spočítaný podiel 0/0 ako smernica priamky vedenej dvoma bodmi, keď tieto dva body splynú. Dostávame ako správne riešenie všetky priamky.

Neurónka sa ale na naliehanie zúfalých programátorov predsa len nakoniec zľutovala a explicitne rozviedla pár protiargumentov proti deleniu nulou.
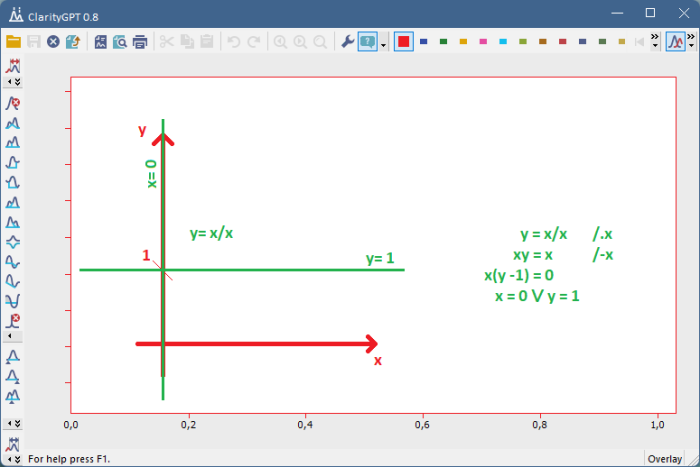
Mnohé z nich údajne chybne využívajú simplifikáciu výrazu, aby dostali spory typu 1 = 2. Čím sa bohužiaľ dopúšťame chyby cyklického dôkazu, pretože simplifikácia výrazu typu “x/x” predsa nie je axióma a teda ju musíme odvodiť, a celkom očividne jej odvodenie závisí na hodnote výrazu 0/0.

Obr.5: Oprava relácie y= x/x, na ktorej stojí celá metóda simplifikácie. Vidieť, že prípad x= 0 treba stále kvôli jeho odlišnej povahe riešiť zvlášť..

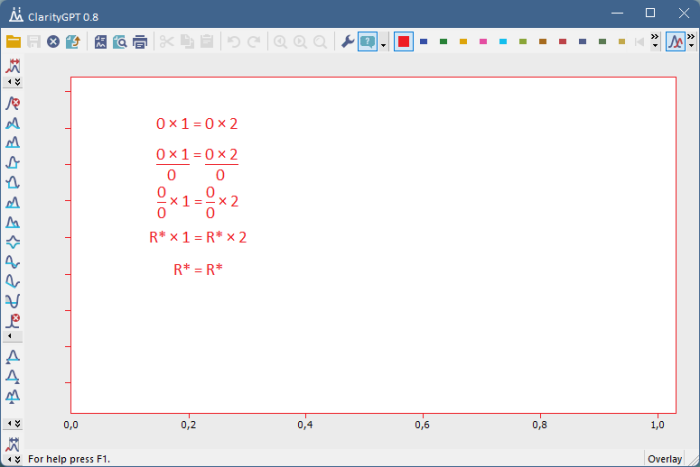
Obr.6: ..a následný príklad správne prevedeného delenia.

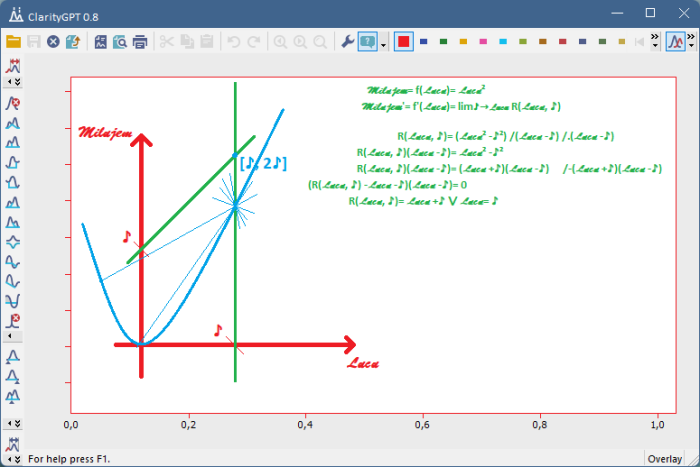
V prípade rozdielnych hodnôt limít zas neurónka vyargumentovala, že limita “typu 0/0” nie je 0/0. Limita sa používa len na výpočet uzáveru množiny, ktorou relácia nepochybne je, takže dostávame len bezosporné lim_{Milujem⇾Lucu} R(Milujem) ⊆ R(Lucu). Pekne to vraj vidieť na príklade derivácií, kde podiel (f(Milujem) – f(Lucu))/(Milujem - Lucu) predstavuje reláciu smernice priamky vedenej dvoma bodmi [Milujem; f(Milujem)] a [Lucu; f(Lucu)], zatiaľ čo príslušná limita predstavuje iba smernice dotyčníc, čo je skutočne podmnožina smerníc všetkých priamok vedených daným bodom.

Obr.7: Výpočet a zobrazenie relácie, ktorá popisuje smernicu dotyčnice pri hľadaní derivácie funkcie Milujem= Lucu². Metóda spočíva v disjunkcii priamky relačnej povahy a následnom uzávere zostávajúcej množiny, čím dostávame hľadanú deriváciu v priesečníku oboch priamok.

 

##seznam_reklama##

Poskytnutých opráv bolo samozrejme viac, ale tým tu dnes nechceme čitateľa unavovať. Aké bola ale prekvapenie vývojárov, keď zistili, že neurónka sa medzičasom naučila derivovať aj spojité nehladké funkcie. Veľmi sľubne začínajú vyzerať aj vyhliadky pri derivácii neholomorfných funkcií a črtá sa tu aj možné riešenie Riemannovej hypotézy.

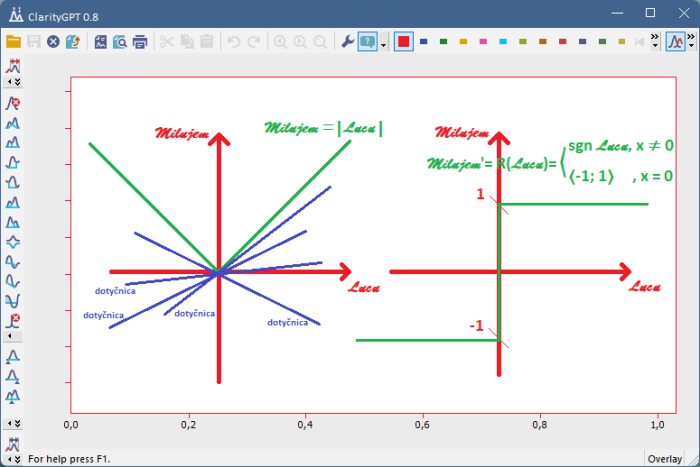
Obr.8: Výpočet relačnej derivácie funkcie Milujem= |Lucu| v nule ako konvexného obalu krajných hodnôt limít.

 

Obr.9: Tieto čerstvo obdržané výpočty výrazu 0/0 vrhajú ďalší tieň pochybností na súčasnú Obecnú relativitu, z ktorej plynie 0/0= 1. Einstein sa medzitým už stihol post mortem vyjadriť, že on iba žartoval. Pár zamestnancov DataApexu k tomu dodalo, že vskutku v každom slušnom vesmíre býva väčšina píkov kladných.