Galileo Galilei (1564–1642) je obecně znám hlavně jako astronom. Byl geniální pozorovatel, navíc konstruktér řady přístrojů (viz Galileo Galilei – Vynálezy a astronomické objevy). Obecně známé je taky pronásledování od inkvizice, méně lidí ví o problémech jeho nauky i osobních vztahů (viz Galileo Galilei, problémy a inkvizice). Zbývá ovšem pojednat jeho fyziku, vždyť Galilei je jedním ze zakladatelů novodobé podoby této vědy. Leckdo si snad vybaví aspoň volný pád. Někdo zná i „Galileiho princip relativity“ a „Galileiho transformaci“ popisující převod pohybu mezi inerciálními soustavami. Skončím otázkou, proč Galileiho kritizovala řada významných filosofů celého 20. století, dokonce napříč spektrem škol, málem „napříč politickým spektrem“. Není to ostuda novodobé filosofie? (Za sebe si myslím, že je, ale není to většinové mínění.)

 

Fyzika před Galileim

Latinský středověk znal různé koncepty fyziky, ale nejvlivnější bylo komentování Aristotela. Pozemskou přírodu viděl jako natolik chaotickou, že neumožňovala matematický popis jevů, ten byl možný pouze v supralunární oblasti. Tu pojednávala geometricky koncipovaná astronomie. Pozemská fyzika vykládala přírodní jevy na základě živlové nauky a jako příklady obecného pojetí změny. Mohl to být docela pěkný pohádkový popis, jenže si hrál na vědu, takže žádné poetické pochopení nevysvitlo. Mnozí lidé si myslí, že živly jsou něčím prastarým, ale zavedl je až v 5. století před n. l. Empedoklés. Aristotelés učinil z jeho živlové nauky školní výkladové schéma. Například pohyb ve smyslu změny místa chápal jako tendenci k zaujetí „přirozeného místa“. Proto kámen padá k zemi, zatímco oheň stoupá vzhůru. Pohádka končí v okamžiku, kdy Aristotelés uplatní hledisko poznání, totiž „hledání podstat a příčin“. Nic se neděje bez příčiny a každá příčina je součástí celého řetězce příčin. Dnes něčemu podobnému říkáme mechanismus účinku. To by se však Aristotelovi nelíbilo hned ze dvou důvodů: Chce ty řetězce příčin navázat na jedinou „první příčinu“; navíc tuto „příčinu účinnou“ (scholasticky: causa efficiens) provazuje s „příčinou účelovou“ (causa finalis), aby vše směřovalo také k jednotnému cíli. A už se ocitáme v metafyzice první příčiny a posledního účelu, dokonce i prvotního hybatele. Původně kvůli metodě fyziky, ne kvůli náboženství. Náhoda nemá žádnou roli, vlastně vůbec není. To je zásadní rozdíl oproti Empedokleovu popisu živlů, který byl opravdu náboženský, ale obešel se bez globálního účelu. Náboženství se podle nového mustru časem předělá taky.

V pozdním středověku a na prahu renesance se znovu objevily i zajímavější koncepty fyziky. Ve 14. století pracovali ockhamisté se skeptickými motivy, někteří dokonce s atomismem, studovali pohyb těles v pravoúhlých souřadnicích, propracovali se k pojmu hybnosti (impetus). Pokus o matematický popis pohybu byl zatím komplikován tím, že nezanedbali tření, takže i k udržování pohybu např. vozíčku byla potřeba síla úměrná jeho hmotnosti. Z jiných pozic vytvořil v 15. století Mikuláš Kusánský představu prostoru bez privilegovaných míst a vedle toho popsal i řadu svých experimentů.

 

Galileovské úvahy

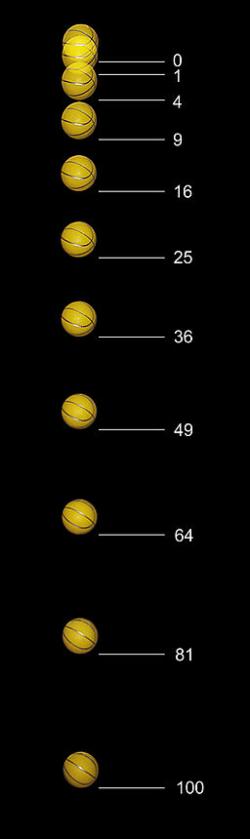
Jakožto zručný a důvtipný experimentátor zkoušel Galilei měřit průběh řady přírodních jevů. Patří k zakladatelům fyziky ve smyslu vědy založené na měření, tedy na matematicky pojednaných výsledcích pozorování nebo experimentů. Přírodní jevy jsou vyloženy matematickou schematizací. Některé parametry jsou dané už intuitivně, ale stejně je potřeba zjistit, zda s nimi měření není v konfliktu. Například lineární nebo kvadratické úměry mezi veličinami. Jiné parametry nezbývá než měřit, v pozdějším pochopení to jsou konstanty, které (přinejmenším na daném stupni poznání), nejsme schopni odvodit z teorie. Takhle vyloženo je to až pozdější metodologická úvaha, ale Galileiho dílo je s ní většinou v souladu a postupně k ní vede. Příkladem lineární závislosti jsou parametry rovnoměrného pohybu, příkladem kvadratické závislosti volný pád. Avšak akceleraci volného pádu, rychlost zvuku nebo rychlost světla nezbývá než naměřit.

Ozvěna je jev známý odedávna a už antičtí autoři ji vykládali jako projev toho, že rychlost zvuku je konečná. Galilei se rozhodl ji změřit a přibližně vzato uspěl. Neúspěšné bylo jeho měření rychlosti světla. Přesto to byl svého druhu úspěch, totiž určení dolní limity, dané rozumně odhadnutými možnostmi použité techniky.

Úměry mezi veličinami známe odjakživa. Každý přece ví, že když je to někam dál, tak tam cesta trvá déle, ale když přidá do kroku, tak tam bude dřív. Bylo by moc divné, kdyby s tím nepočítali i ostatní živáčkové, i když k tomu nepotřebují teorii ani čísla; většina lidí to taky zvládá i bez teorie. Přírodovědce však tato zkušenost zajímá také teoreticky. V plné parádě se ovšem úměry odhalí až poté, co dokážeme odhlížet od všemožných „zkreslujících“ jevů. Musíme odhlédnout hlavně od tření a odporu prostředí, plus od reálných odchylek od rovnoměrnosti. To není povrchní zanedbání, ale rozklad situace na jednotlivé komponenty, které popisujeme nejprve každou zvlášť.

Důležitým příkladem rozumného odhlížení od okolností, které jsou v jiných kontextech velice důležité, je pád kamene a pád chmýříčka. Padá kámen rychleji proto, že je těžší? Nebo proto, že je z jiné látky? Aristotelskou představu o různé rychlosti pádu různě těžkých těles zpochybňovali už scholastici 14. století, většinou ale jen mentálními experimenty. K pokusům s pády proto patří i ověření představy, že různě hmotná tělesa padají stejně rychle, tedy pokud vezmeme taková tělesa, u kterých se moc neuplatní odpor vzduchu. Vlastně to vůbec není samozřejmé, nejen proto, že u hodně lehkých předmětů nebo u věcí s velkou plochou máme zřetelnou zkušenost s odporem vzduchu. („Odpor vzduchu není úměrný ctnosti aviatika“, praví známá průpověď z počátků letectví.) Představa o stejném zrychlení při pádu znamená, že zrychlení není závislé na tom, kolik té hmoty je a jaká je. To je předstupeň k Newtonovým úvahám o gravitační konstantě, nezávislé na tom, o jakou hmotu se jedná.

Na okraj si neodpustím poznámku, jak může i nesmyslně zjednodušená a pomršená verze původně chytré teorie po staletích inspirovat. Galileo skoro jistě četl Lucretia. Ten referuje, že podle Epikúra padají všechny atomy stejně rychle. Démokritos by se štítil takhle zjednodušeného převodu změn konfigurací atomů na jejich pád, ale Galilei uměl vyhmátnout, o co jde, a ne se zabývat nějakou převážně absurdní ontologií. Místo dedukování z metafyzických principů má nastoupit nová věda.

 

Akcelerace volného pádu

Některé popularizace navozují představu, že Galileo Galilei házel závaží z horního patra šikmé věže v Pise a na jednotlivých nižších ochozech měřil neexistujícími stopkami čas průletu. To by spíš něco rozbil. Šel na to vtipně. Pád po kolmici nahradil kutálením kovových koulí po šikmé fošně s podélným žlábkem uprostřed, dlouhé 12 loktů, nadzvednuté o 1 loket. Tím zmenšil akceleraci, takže prodloužil čas průběhu. Pokaždé měřil čas k jiné značce na fošně a ukázal, že dráha je úměrná čtverci času. Když fošnu zvedl o 2 lokte, kutálelo se to rychleji, ale vztah dráhy a času platil stále. Úskalím bylo dostatečně přesné měření času. Použil metodu vodních hodin, známou už v antice a precizovanou v díle Mikuláše Kusánského O pokusech s váhami (De staticis experimentis) z roku 1450. Voda po dobu měření vytéká z trubičky u dna větší nádoby do misky, pak je třeba vyteklou vodu zvážit. Celý pokus byl v letech 1960 až 1973 podle Galileiho pracovních poznámek z roku 1604 vícekrát úspěšně zopakován.

Udává se však ještě pokročilejší a důvtipnější způsob, který zvlášť dobře odpovídá Galileiho povaze. V roli značek prý na fošně napnul napříč struny tak, aby jejich rozestupy mohl nastavovat. Tím vytvořil cosi jako hudební nástroj, každá struna vydala při kolizi se závažím tón. Nastavováním rozestupů mezi strunami docílil rovnoměrných časových rozestupů mezi tóny. Ty měřil hrou rychlé italské písničky, jejíž rytmus sloužil jako synchronizační takt. Nepotřeboval znát délku těchto časových intervalů číselně, stačila jejich stejnost. Takhle mohl získat přesnost pod desetinu vteřiny. Když to po nesčetných úpravách konečně fungovalo, tak proměřil rozteče mezi strunami. Rostly geometrickou řadou. (K měření konstanty zrychlení jsou ovšem potřeba ty vodní hodiny, ale po tomto pokusu už stačí měřit jen čas na celé dráze.)

Galileiho princip relativity

Název je to novodobý, spíš na Galileiho počest, sám princip je naopak mnohem starší. Známý příklad je chvilková nejasnost podřimujícího cestujícího kvalitní železnicí, zda se pohybuje vlak nebo nádraží. Když to nedrncá, tak to rozhodne jenom zkušenost, že naše nádraží i koleje bývají pevně spojeny se zemí, zatímco vlaky nikoli. Dávný příklad je problém rychlostí dvou lodí, pokud zrovna pečlivě nesledujeme okolní pevninu. Staré příklady předjímají Newtonovu fyziku, totiž že když to nedrncá a hlavně citelně neakceleruje nebo nebrzdí, tak je volba popisné soustavy pouze smluvní záležitostí, protože vztahy dráhy rychlosti a času jsou v každé z těchto soustav stejné. Říkáme tomu inerciální soustavy. Novodobé školní příklady řeší rychlost pohybu cestujícího chodbičkou jedoucího vagónu, v krajním případě vůči jinému v protijedoucím vlaku. Formálnímu řešení dnes říkáme Galileiho transformace. A když se pohyby dějí šikmo, tak musí nastoupit vektory a počítání úhlů se sinusy. (Šelma běžící šikmo ke kořisti to zaokrouhleně zvládá i bez kalkulačky, jaksi analogově, podobně i většina lidí; ti ani při dobíhání vlaku většinou nemyslí na Galileiho transformaci, naštěstí.)

Už řecké hermetické spisy psané v římské císařské době probírají pohyb plavce v řece nebo mořském proudu, a to v různých situacích: po proudu, proti proudu, rychlejší nebo pomalejší než proud; kolmo na proud, šikmo. Z kontextu je jasné, že už tehdy šlo o běžná školní cvičení, pocházející nejspíš z helénistické doby (ca 3. století před n. l.).

Po někom z doby mezi dávnými řeckými učenci a Newtonem se to pojmenovat muselo, tak to padlo na Galileiho. O matematizaci pohybů se zasloužil. Dokud vystačíme s malými rychlostmi (vůči rychlosti světla) a malými hmotnostmi (tak do hmotnosti Země až Slunce) a obvykle potřebnou přesností (nikoli krajně přesná astrometrie nebo satelitní navigace), tak s tím dobře vystačíme. V ostatních případech na to musí přijít Einstein.

 

„Dvě nové vědy“

Výsledky velké části svých fyzikálních pokusů Galilei publikoval až roku 1638 v díle Matematické rozpravy a pokusy, týkající se dvou nových věd (Discorsi e dimostrazioni matematiche, intorno à due nuove scienze). Těmi novými vědami jsou „mechanika“ ve smyslu statika, včetně problematiky pevnosti materiálů, tedy předstupně materiálového inženýrství – a „nauka o pohybu“, kinematika. Na jedné straně je to typická galileovská nadsázka a div ne chvástavost, protože tyto nauky rozhodně nové nebyly, přinejmenším ne ve srovnání s řeckou antikou. Na druhé straně v nich Galilei učinil významné objevy a postavil je na nový základ. Tím se opravdu stal jedním ze zakladatelů nové vědy v obecnějším smyslu slova, novodobé fyziky. (Dynamiku, tedy popis sil souvisejících s pohybem, přidá až Newton.)

 

Za zmínku stojí i probíraná statika. Krom úvah o těžišti a síle na páce totiž obnovuje povědomí o tom, že pevnost trámu je úměrná jeho průřezu, který roste s druhou mocninou celkové velikosti, zatímco jeho „váha“ roste s třetí mocninou, navíc ještě ta delší páka. Výsledkem je, že pevnost konstrukce nelze ověřovat na zmenšeném modelu bez posunutí poměrů velikosti a „tloušťky“ konstrukčních prvků. (Jinak stavba padne jako katastrofická lanovka Řeka Zorby.) To samozřejmě znali stavitelé už od klasické řecké antiky, teoreticky to pojednal nejpozději Archimédés začátkem 2. století před n. l., ale v novověku se to často a celkem právem připisuje právě Galileimu. Je však možné, že Galilei byl opravdu první, kdo tyto úvahy vztáhnul také k tvarům kostí živočichů. Takže nejspíš zakladatel biomechaniky! Každopádně pečlivý a důvtipný pozorovatel všemožných přírodních a technických jevů.

 

Asi platí, že co udělal Kepler pro astronomii, to Galilei pro fyziku. Škoda, že vývoj evropské vědy nešel v této linii, třeba prostřednictvím Pierra Gassendiho (1592–1655), což byl astronom a filosof, znalec Epikúra, který polemizoval s Descartem. (Gassendimu jsem věnoval závěrečnou část článku Přechod Merkuru před Sluncem v pondělí 11. 11. od 13:35.) U přírodovědců požívá Galilei oprávněnou úctu, ale leckteří jiní nad ním ohrnují nos. Jedním z důvodů bylo, že dlouho nebyly publikované jeho pracovní poznámky z roku 1604. Dalším důvodem je převládající snaha naroubovat vznik novověké vědy na zcela jinak stavěné myšlenky Reného Descarta. A nakonec i časté tesknění po aristotelské metafyzice.

 

Proč se Galileiho pokusy nelíbily historikům vědy

Galilei byl v 20. století podezřívaný málem z toho, že si své pokusy vymyslel, zvláště pokud jde o zrychlení volného pádu. Před opožděným uveřejněním jeho poznámek (zvl. folia 116v) si málokdo uměl představit, jak technologickými prostředky raného 17. století měřit dostatečně přesně krátké časové úseky. I mentální experimenty sice mohou mít ve vědě své místo, ale tenhle spor byl jiný případ.

Trochu rozumnější byla kritika, kterou představil Alexandre Koyré (1892-1964), historik vědy a náboženství, ovlivněný také Husserlem. Tvrdil, že Galilei odvodil zákon volného pádu analyticky, a pokusem pak pouze demonstroval, že se jev chová nějak podobně, že není s tímto odvozením ve frapantním rozporu. (Někteří pozitivisté zase trvali na tom, že jakýkoli zákon se má odvozovat čistě induktivně.) Dnes víme, že Galilei závislost dráhy na druhé mocnině času opravdu dokázal změřit. A snad se už nebudeme tak úporně hádat o to, co je deduktivní, a co induktivní, protože v reálu mezi tím nové myšlenky často nějak oscilují.

Při tehdejších technických možnostech by tupé (nezaujaté) nemehlo nemělo šanci změřit zrychlující pohyb závaží natolik přesně, aby se ukázalo, že dráha roste právě a přesně s druhou mocninou času. Galileo však nebyl tupý, ani nemehlo. Měl svůj tip a uměl měřit. A ten tip mu opravdu vyšel. První (obecnou) úrovní toho tipu je sázka na možnost matematického popisu kvantifikovaných přírodních jevů. Druhou úrovní (konkrétně pro tento případ) je sázka na rovnoměrné zrychlování pohybu padajícího tělesa, neboť to je v nejlepší shodě s neměřitelnou životní zkušeností, s citem fyzika a s intuicí matematika. Měření tyto sázky silně podpořilo. Novodobí hyperkritici, kupodivu ne z řad skeptiků, ale neoscholastiků, fenomenologů a postmoderních myslitelů, by mohli poukazovat na to, že není nijak dokázáno, že jde přesně o druhou mocninu, ale tímto směrem snad žádná z kritik nemíří. Galilei opravdu nezjistil pravděpodobnost, s jakou exponent 2,00 odpovídá výsledkům pokusu lépe než třeba 1,99. To by však napadlo jenom šílence – nebo důvtipného vědce, hledajícího (zatím marně) novou fyziku, ale v mnohem pozdější době.

Kritika Galileiho z řad novodobých filosofů

Nejslavnější a naštěstí i nejslušnější kritiku Galileiho podal Edmund Husserl (1859-1938) ve svém pozdním díle Krize evropských věd a transcendentální fenomenologie. Nic proti Němcům, nic proti Židům, Hanákům, matematikům a filosofům. Je ovšem obecně známo, že každí z nich myslí a mluví poněkud svérázně, takže když německý Žid z Prostějova vystudoval v Německu matematiku a filosofii, a pak založil specifickou filosofickou nauku, tak lze očekávat, že jeho dílo nebude snadným čtením. Není. Galileiho kritizuje proto, že prý zaměnil prožívaný svět (Lebenswelt) za jeho matematizovaný obraz. Zaznívá zde motiv „odkouzlení světa“, který při kritice vědy použil už Friedrich Jacobi (1743-1819). Přesto je Husserl velice racionální duch a nehodlá novověkou vědu znevažovat, pouze upozorňuje, že „neřeší otázky smyslu“. To lze komentovat tím, že k tomu přece věda není; a že každé nové poznání je podobné novému okouzlení, které samozřejmě odkouzluje ono starší, naivnější. A historicky vzato Galilei zdaleka nebyl první, kdo matematizoval jevy v pozemském světě. Začali s tím už Filoláos a Archytás, ale antikou se Husserl nezabýval. Husserlovo upozornění by ovšem bylo trefné, pokud by vědci zaměnili skutečný svět za formalismus matematických objektů (jako Descart). Jenže, co je „skutečné“? (Já myslím, že to, čím poměřujeme teorie, tedy pozorované jevy, ale je to věc názoru.)

Řeckými filosofy se inspiroval Husserlův svérázný a konfliktnější odchovanec Martin Heidegger (1889-1976). Začínal však studiem středověké filosofie a teologie, což ho poznamenalo. Každopádně natolik tesknil po aristotelském rozdělení pozemské a nebeské oblasti, že je nehodlal ničím odkouzlovat. V řadě jiných úvah předvedl mistrovství, ale k našemu tématu se vyjádřil výkřikem „Věda nemyslí!“ Ke stáru ho štvaly kosmické lety, nejvíc lety lidí na Měsíc, které prý narušily bytostnou skutečnost, že člověk je pozemšťan.

Dobře, fenomenologové si s Galileim nerozumí. Že odkouzlení vadilo i existencialistům, je očekávatelné. Tím spíše filosofům z konzervativních kruhů. Ale že se ke kritice galileovské přírodovědy přidá i významná část postmoderny, to už by jeden nečekal! Opět vadí matematizace. Pominu blázniviny typu „zakladatel tvrdé marsovské falokratické fyziky na úkor tekuté ženské venušanské“. Jenže s Galileim se dobře nevypořádal ani svobodomyslný Paul Feyerabend (1924-1994). Proč se tolik filosofů pořád nostalgicky ohlíží po aristotelském pojetí světa a po antropocentrickém pojetí filosofie? To by bylo na dlouhé lokte.

Významné rozcestí filosofie

Většina filosofů ctí Sókrata, zatímco přírodovědci zase Galilea a Darwina. Jen obtížně se hledají výjimky. Tradičně orientovaní filosofové ctí účel a „smysl“, formalistnější zase logiku dialogů, odkaz na Sókrata uspokojí obojí. Navíc prý Sókratés „obrátil zájem k věcem lidským“, takže filosofie byla nakonec zařazena mezi humanitní vědy. Galilei je opakem Sókrata v téměř každém ohledu.

Kdybychom mohli dějiny čehokoli nahlížet skrze nějaké „kdyby“, povzdechl bych si, že nebýt úspěchu Descartovy filosofie, tak by filosofové i přírodovědci byli ušetřeni matematické povahy „objektivní reality“ i subjektu a objektu; filosofové navíc ega a kultu vědomí i duality ducha a hmoty, resp. duše a těla. Cesta, kterou šli Galilei a Gassendi, působí mnohem příčetněji (a to nejsem epikúrejec), bohužel se nestala obvyklou součástí filosofie.

Závěrečné poděkování a omluvy

Děkuji znalejším přátelům, z jejichž znalostí a myšlenek jsem v článcích o Galileim hojně čerpal. Nejmenuji je jen proto, aby případné moje chyby nepadly na jejich hlavy. Omlouvám se, že nemám pramenné texty dost nastudované, je to už moc daleko od mé odbornosti i jazykové schopnosti. Můj nesouhlas s kritikou Galileiho je ovšem specifické téma, se kterým nemusí každý souhlasit.

Literatura

Galileo Galilei na české Wikipedii.

Aristotelés: Fyzika. Praha: Rezek 1996.

Edmund Husserl: Krize evropských věd a transcendentální fenomenologie: úvod do fenomenologické filozofie. Praha: Academia 1996.