Rozdíly mezi hmotou a antihmotou lze pozorovat
Existují například pouze levotočivá neutrina a pravotočivá antineutrina Také mají u částic a antičástic některé typy stejných rozpadů různé pravděpodobnosti. Podrobnější popis těchto rozdílů a jak nám umožňují sdělit radiovými vlnami vzdálenému mimozemšťanovi, že jsme z hmoty a ne antihmoty, a která strana je levá, je v jednom ze starších článků.
Zatím však předpokládáme, že hmotnost a velikosti náboje i magnetického momentu jsou pro částici a antičástici shodné. Pozorování rozdílu u těchto veličin by mělo fundamentální dopady, protože by vedlo na narušení základní součásti standardního modelu hmoty a interakcí, tzv. CPT symetrie. Ta říká, že fyzikální zákonitosti a procesy, které popisují, musí být úplně stejné, jestliže současně změníme znaménka os (přejdeme do světa v zrcadle – tzv. P symetrie), zaměníme částice za antičástice (přejdeme do antisvěta – C-symetrie) a změníme směr toku času (T-symetrie). Narušení P-symetrie a C-symetrie pozorujeme docela často, viz třeba zmíněná existence pouze levotočivého neutrina. Většinou se vzájemně vyruší a kombinovaná CP-symetrie pro situaci, kdy uplatníme přechod ze světa do antisvěta v zrcadle, pak platí. Pozorujeme však i slabá narušení této kombinované symetrie a právě ta nám umožňují zmíněnou možnost informovat mimozemšťana o tom, co je pro nás antihmota a levá strana.

Pokud platí CPT-symetrie, mají antičástice stejnou hmotnost a velikosti náboje i magnetického momentu jako částice, liší se jen znaménkem. Její platnost, která vede k neměnnosti fyzikálních zákonitostí při Lorentzově transformaci a stojí tak v základech nejen teorie relativity, lze pak experimentálně ověřovat právě pomocí srovnání hmotností, nábojů a magnetických momentů částic a antičástic. Případné zjištění, že CPT symetrie neplatí, by znamenalo hodně velkou změnu jednoho ze základních paradigmat fyziky. To je také důvod, proč se tato extrémně přesná měření provádějí.
Jak velikost hmotnosti, náboje a magnetického dipólového momentu měřit?
Experimenty, které se studiem rozdílů mezi vlastnostmi hmoty a antihmoty při nízkých energiích zabývají, využívají unikátní zařízení v evropské laboratoři CERN, kterým je antiprotonový zpomalovač. Ten používá protony urychlené na rychlosti blízké rychlosti světla pro produkci antiprotonů v jejich srážky s těžkými jádry v terči. Vzniklé antiprotony, které mají také relativistické rychlosti, jsou pomocí magnetického pole vyvedeny do zmíněného antiprotonového zpomalovače. Jde vlastně o obrácený urychlovač. Ten vyrovná jejich rychlosti, takže se jejich vzájemný chaotický pohyb zmenšuje. Protože střední kinetická energie tohoto pohybu charakterizuje teplotu daného souboru částic, můžeme říci, že se teplota antiprotonového plazmatu ve svazku sníží. Co je ale nejdůležitější, antiprotonový zpomalovač postupně sníží energii a rychlost usměrněného společného pohybu antiprotonů a předá je jednotlivým experimentům, které je mohou zachytit do magnetických pastí. Tam se s nimi pracuje, buď se zkoumají přímo antiprotony, nebo se vytvářejí atomy antivodíku, či kombinace helia a antiprotonu.
Nejmenší problém je s určením setrvačné hmotnosti antiprotonu, která je už delší dobu známá s podobnou přesností jako setrvačná hmotnost protonu, tedy s relativní nejistotou 1:10-11. Měření rozdílu hmotností těžších jader a antijader a poměru mezi jejich nábojem a hmotností bylo v roce 2015 publikováno experimentem ALICE a je popsáno zde.
U určování gravitační hmotnosti je situace mnohem složitější. Možnosti jsou popsány i s některými měřeními dalších veličin v dřívějším článku. V současné době je nejpřesnější měření gravitační interakce mezi hmotou a antihmotou a gravitační hmotnosti antičástic na velmi nízké úrovni přesnosti. Ta sice ukazuje na shodu gravitačních hmotností vodíku a antivodíku, ale v mezích experimentálních nejistot je dokonce pořád ještě i možnost gravitačního odpuzování hmoty a antihmoty místo přitahování, které se předpokládá a odpovídalo by obecné teorii relativity. Na zpřesnění těchto měření se intenzivně pracuje.
První spektrometrie antivodíku spektrometrem APLHA
V minulých letech jsme byli u experimentů pracujících na antiprotonovém zpomalovači svědky velkého zlepšení v produkci a udržení antivodíku v magnetické pasti. Připomeňme, že neutrální antivodíky jsou v tomto případě držený pouze díky svému magnetickému dipólovému momentu (jsou malými magnetkami). Hlavní pokrok je spojen s experimentem APLHA. Prvních 5000 antivodíků se podařilo vytvořit experimentu ATHENA v roce 2002. První fáze experimentu ALPHA byla zahájena v roce 2006 a první dlouhodobé udržení neutrálního antivodíku v magnetické pasti proběhlo v roce 2010 a týkalo se celkově pár desítek antiatomů a doby udržení v řádu stovek milisekund. V roce 2011 už to bylo celkově několik stovek antiatomů a zhruba dvě desítky už vydržely až 1000 s. Délka udržení je důležitá i kvůli tomu, aby byla jistota, že jsou antivodíky v základním stavu a je dost času na experimentování s nimi. Při těchto měřeních se v každém jednotlivém procesu zachytávání a udržování antivodíků v průměru podařilo udržet 1,2 antivodíku.

V roce 2012 se podařilo první měření přechodu v atomu antivodíku. Pomocí mikrovlnného záření se inicioval přechod z jedné orientace projekce spinu elektronu v základním stavu atomu antivodíku do druhé. Změna způsobí, že se také změní orientace magnetického dipólového momentu a antivodík z pasti vypadne a anihiluje. Přesnost měření však v tomto případě byla jen omezená.
V prosinci 2016 pak byly publikovány první výsledky spektrometrie antivodíku. Pokrok byl umožněn tím, že se v jednom procesu záchytu a udržování podařilo mít 14 antivodíků. V tomto případě byly antivodíky ozařovány světlem z laseru a pozoroval se přechod mezi základním stavem a prvním excitovaným stavem, tedy mezi stavy 1S a 2S. Vlnová délka záření tohoto přechodu je zhruba 121,5 nm (vlnová délka budícího laseru byla dvojnásobná 243 nm) a pro vodík je energie této čáry změřena s přesností 1:1015. Při těchto měřeních je potřeba vzít v úvahu i změnu vlnové délky v magnetickém poli a to, že každý ze stavů není jednoduchý. Nyní se tedy povedla spektrometrie této linky atomu antivodíku. Ukázala se shoda se stejnou spektrometrií vodíku na úrovni přesnosti 1:1010. Vzhledem k tomu, že energie přechodů ve vodíku i antivodíku závisí na nábojích a setrvačných hmotnostech částic, které je tvoří, ověřuje se pomocí jejich měřením jejich shoda a tím i zachování zmíněné CPT symetrie.
V následujících letech by mělo dojít hlavně ke zvýšení statistiky, nyní se totiž měření provedlo celkově pouze s pár stovkami antivodíků. Velký prostor je stále v zachycování vzniklých antivodíků. Při jednom cyklu se začíná zhruba s 25 000 a končí zatím průměrně u zmíněných 14. Také by se měl určit přesný tvar linky. Zjistila by se tak nejen shoda mezi přechody v antivodíku a vodíku, ale také by bylo možné určit rozložení náboje v antiprotonu. Jednalo by se o stejný způsob, jakým se pomocí hyperjemné struktury přechodů ve vodíku měří rozložení náboje v protonu. V následujících letech tak lze tak v této oblasti očekávat významný pokrok.
Měření magnetického dipólového momentu antiprotonu
Jak už bylo zmíněno, předpokládá zákon zachování CPT symetrie stejnou velikost magnetického dipólového momentu, pouze má být rozdílné jeho znaménko. Kvůli svému magnetickému dipólovému momentu se proton i antiproton chovají jako malé magnetky. A z chování těchto magnetek v magnetickém poli tak můžeme velikost magnetického dipólového momentu určit. Hodnotu magnetického dipólového momentu protonu známe s relativní přesností 2:109.
Zařízení, které se měřením magnetického dipólového momentu věnuje a nedávno získalo zatím nejpřesnější hodnotu této veličiny, je experiment BASE (Baryon Antibaryon Symmetry Experiment). Navazuje na výsledky experimentu ATRAP (Antihydrogene TRAP), jehož nejpřesnější hodnoty pocházejí z roku 2013. Toto zařízení umožnilo získat první velmi přesná měření magnetického dipólového momentu. Pro měření jeho hodnoty využívá Penningovou past, která je typem elektromagnetické nádoby s osovým magnetickým polem a nehomogenním elektrickým polem. Antiproton visí uprostřed kruhové železné elektrody vmáčknuté mezi elektrody měděné. Tepelný kontakt s kapalným heliem drží elektrody na teplotě 4,2 K a je zajištěno téměř dokonalé vakuum. Statické a oscilující pole, které se přivádí na elektrody, umožňuje manipulovat s antiprotonem a zjišťovat jeho elektrické a magnetické vlastnosti. Antiprotony pro analýzu jsou do ní přiváděny ze zásobní pasti, kde jsou po svém zpomalení v urychlovačovém zpomalovači uloženy.
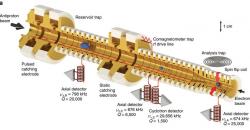
V daném případě se určuje cyklotronová frekvence, ta souvisí s pohybem nabité částice ve statickém magnetickém poli. Dráha je kruhová nebo po spirále s daným poloměrem a frekvencí pohybu. Ta závisí na náboji a hmotnosti částice a intenzitě magnetického pole. Larmorova frekvence je pak frekvence precesního magnetického dipólového momentu. Závisí na intenzitě magnetického pole a právě magnetickém dipólovém momentu. V zařízení ATRAP se podařilo zlepšit přesnost určení magnetického dipólového momentu 680krát oproti předchozím experimentům.
Ještě lepších výsledků pak dosáhlo nové zařízení BASE, u něhož se dosahuje extrémní snížení energie antiprotonů v magnetické pasti. Teplota antiprotonů, která je dána energií chaotického pohybu částic v této plazmě, je v experimentu BASE okolo jednoho stupně nad absolutní nulou. To umožňuje dosáhnout toho, že pak lze oblak antiprotonů udržovat i více než rok. Past tak představuje v podstatě velice sofistikovanou nádobu na antihmotu, ovšem bohužel jen ve velice řídké podobě antiprotonového plazmatu. Z této shromažďovací pasti se pak dá antiproton poslat k měření.
Zařízení BASE umožnilo změřit velikost magnetického dipólového momentu s ještě vyšší přesností. Relativní nejistota je jedna miliontina, tedy ppm, což je zhruba šestkrát menší nejistota než u hodnoty změřené pomocí zmíněného experimentu ATRAP. Hodnota u antiprotonu zjištěná experimentem BASE odpovídá v mezích přesnosti měření velikosti magnetického dipólového momentu protonu. To je však jen začátek cesty, která má umožnit zvýšit přesnost ještě 200 až 800krát, čímž se přesnost měření této veličiny u antiprotonu dostane na úroveň jejího měření u protonu. A každý zjištěný rozdíl v hmotnosti či velikosti náboje nebo magnetického dipólového momentu protonu a antiprotonu by byl okamžitým průlomem do exotické nové fyziky.
Závěr
V nejbližších letech se dá očekávat zlomový pokrok v produkci i uchovávání antiprotonů s nízkou energií a antivodíku. Mělo by tomu pomoci zařízení ELENA (Extra Low ENergy Antiproton ring). Zatím se totiž posílají antiprotony ze zpomalovače s energií 5,3 MeV a ty si je pak musí zpomalit. To však vede k jejich ztrátám. Proto se postavilo zařízení ELENA, které je dalším zpomalovačem, který energii antiprotonů sníží ze zmíněné energie 5,3 MeV na energii padesátkrát menší, tedy 100 keV. Tyto antiprotony se pak už efektivně beze ztrát předají jednotlivým experimentům. To by mělo přispět ke zvýšení statistiky experimentů i kvality získaných dat. První testy zařízení ELENA proběhly už v listopadu 2016. Jeho využívání zlepší kvalitu práce experimentů a vylepšení probíhají i u jejich přístrojů. Lze se tak těšit na další novinky z testování fundamentálních vlastností našeho světa a hranic nové fyziky.
Redakce si dovoluje připojit video: Podrobnější vysvětlení řady aspektů produkce, vlastností antihmoty a významu jejího zkoumání:
Odhalí půvabné kvarky záhady Velkého třesku?
Autor: Stanislav Mihulka (07.06.2017)
Diskuze:
Jestliže umí urychlovač urychlit hmotu,
Karel Rabl,2017-02-06 01:39:14
blízké rychlosti světla co kdyby se měřilo, třeba různé změny blízkého okolí právě při průletu těchto částic a bez nich, podobně jak se to děje v "sychnchnotronu" s elektrony třeba čas, frekvence nebo měření velikostí od atomů až po různé změny délek uvnitř nebo i vně "trubice" ve které tyto atomy se pohybují?
výborný článek - děkuji!
Pavel Brož,2017-02-05 21:00:09
Jenom dodám pár úvah ohledně možného narušení CPT a Lorentzovské invariance na extrémně malých škálách. Poslední zpřesnění při experimentálním testování platnosti CPT symetrie a tím i Lorentzovy invariance fyzikálních zákonů je určitě dobrou zprávou pro stávající modely, které Lorentzovsky invariantní jsou. Navíc lze předpokládat, že s Lorentzovsky invariantní fyzikou si ještě hodně dlouhou řádku let vystačíme. Přesto všechno už dnes existují dobře podložené úvahy o tom, že Lorentzova symetrie a tím také CPT symetrie může být nějakým způsobem narušena na škálách, na kterých se budou význačně projevovat kvantové fluktuace gravitace. Za takovou škálu se dnes všeobecně považuje tzv. Planckova délka, která je řádově rovna 10^-35 metru. Fyzika na této škále bude ještě hodně dlouho netestovatelná, protože na každý řád snížení testovatelné škály potřebujeme jeden řád zvýšení energie částic v urychlovačích, takže jestliže si dnes s maximální energií urychlovače LHC řádově 10 TeV dokážeme „osahat“ fyziku na škále až do cca 10^-19 metru, tak na otestování fyziky na Planckově škále nám stále ještě 16 řádů energie chybí. Z toho tedy plyne, že Planckova škála vysoce pravděpodobně nebude v 21. století pokořena, a proto také úvahy o fyzice na této škále budou ještě hodně dlouho pouhými teoretickými spekulacemi.
Nicméně pokud se přesto vydáme na tento tenký led spekulací o fyzice na Planckově škále, tak existují docela rozumně znějící důvody, proč by se tam mohla narušovat Lorentzova invariance. Jedním z těchto důvodů je právě sama existence nějaké fundamentální škály. Touto sice nemusí být nevyhnutelně Planckova délka, jak si dnes většinově myslíme nejen pod vlivem různých variant teorie superstrun, stejný problém totiž vznikne pokaždé, když prohlásíme, že existuje nějaká fundamentální škála, na které se fyzika začíná výrazně odlišovat od fyziky nad ní. Jedná se totiž o to, že díky Lorentzově kontrakci délek by se dva vůči sobě se pohybující pozorovatelé pozorující ze dvou soustav tentýž experiment nemuseli shodnout, kdy by se efekty nové fyziky měly začít projevovat. Tak např. první pozorovatel by se dejme dostal až k pozorování „detailů“ o rozměrech 10^-30 metru, tedy pět řádů nad Planckovou škálou, tedy z jeho pohledu by vůbec nebylo nutné započítávat nějaké kvantové gravitační fluktuace. Tato škála 10^-30 m by se ale pro dostatečně rychle se pohybujícího druhého pozorovatele mohla jevit díky Lorentzově kontrakci jako už srovnatelná s Planckovou délkou, a z jeho pohledu by se už efekty kvantové gravitace tedy měly projevovat.
Právě uvedený argument má ve skutečnosti své mouchy a dá se s ním dlouze polemizovat – jedná se zejména o to, že a priori opravdu nelze vyloučit, že oba pozorovatelé uvidí hodně rozdílné efekty, jeden např. ještě neuvidí projevy kvantové gravitace, zatímco druhý už ano, a to při pohledu na tentýž experiment. Přitom všem by tvar fyzikálních zákonů opravdu mohl zůstat stejný pro oba, a to je vlastně přesně to, co Lorentzova invariance požaduje. Nicméně dnes ještě s jistotou neznáme fyzikální zákony platné na Planckově délce. Dnes používané a dnes testovatelné fyzikální zákony neobsahují žádnou fundamentální délku, z jejich pohledu tedy nedochází k nějaké radikální proměně fyziky na extrémně malých škálách. Máme samozřejmě ale také teorie, dnes ještě netestovatelné, které fundamentální délku obsahují, a ty se k danému problému staví různě. Některé z těchto teorií, např. různé varianty teorií superstrun, sice fundamentální délku obsahují, ale Lorentzova invariance se v nich nenarušuje. Jiné teorie naopak předpokládají, že na příslušných škálách k narušení Lorentzovy invariance dochází, mezi vícero takovými lze zmínit např. Hořavovu teorii gravitace, což byla vůbec první renormalizovatelná kvantová teorie gravitace konzistentní ve čtyřech prostoročasových dimenzích (zatímco teorie superstrun jsou konzistentní pouze v 10, a tzv. M-teorie pouze v 11 prostoročasových dimenzích, čímžto se v nich musí uměle vymýšlet komplikované mechanismy tzv. kompaktifikace, které mají za úkol se těch přebytečných dimenzí zbavit). Mimochodem, Petr Hořava dodnes patří mezi uznávané strunové teoretiky, kteří výrazně přispěli k rozvoji teorie superstrun, proto bylo docela překvapení, když přišel s teorií zcela mimo její rámec.
Otázka Lorentzovy invariance úzce souvisí také s otázkou existence či neexistence nějaké privilegované inerciální soustavy. Připomeňme, že speciální teorie relativity vznikla právě na základě odmítnutí existence takové privilegované soustavy. Dokonce ještě i před vznikem speciální teorie relativity platilo, že privilegovaná soustava neexistuje, pokud pracujeme jenom se zákony Newtonovy mechaniky, a taktéž neexistovala, pokud jsme pracovali jenom se zákony Maxwellovy elektrodynamiky. Problém nastal teprve tehdy, pokud se pracovalo s oběma dohromady, tedy jak s Newtonovou mechanikou, tak s Maxwellovou elektrodynamikou, a to protože každá z nich používala pro přechod do pohybující se soustavy jinou transformaci – Newtonova mechanika používala Galileiho, zatímco Maxwellova elektrodynamika Lorentzovu transformaci, a pokud by tento stav měl zůstat, pak nevyhnutelně existovala význačná soustava, v níž platily v původní podobě jak zákony Newtonovy mechaniky, tak zákony Maxwellovy elektrodynamiky, zatímco v jiných, vůči té význačné se pohybujících soustavách, bychom už měli být schopni najít odchylky od „původní formulace“ fyzikálních zákonů. Takováto význačná soustava se nazvala éterová soustava nebo kratčeji přímo éter (éter mělo být hypotetické prostředí, jehož kmitání se mělo projevovat jako elektromagnetické vlny, podobně, jako se kmitání v hmotném prostředí projevuje jako zvuk). Speciální teorie relativity odmítla představu éteru, tedy i představu význačné inerciální soustavy, vynutila si modifikace zákonů Newtonovy mechaniky, které v nové podobě byly Lorentzovsky invariantní, nikoliv postaru Galileovsky invariantní, a tím pádem celá fyzika opět vypadala stejně ve všech libovolně rychle se pohybujících inerciálních soustavách.
Pokud by byla Lorentzova invariance na extrémně malých škálách narušena, znamenalo by to tedy také jakýsi „návrat éteru“, ne nutně ve smyslu nějakého hmotného prostředí, ale minimálně ve smyslu existence význačné inerciální soustavy. Zde je dobré dobře zvážit argumenty, které by podobný krok měly ospravedlnit. V první řadě je nutné si uvědomit, že i na makroskopické úrovni platí neexistence význačné soustavy pouze za předpokladu, že se nacházíme v plochém prostoročase (tedy v prostoročase, s nímž pracuje speciální teorie relativity). Pokud se nacházíme v zakřiveném prostoročase, tak přechod do pohybující se soustavy poznáme velice dobře, protože zakřivený prostoročas vypadá z obou těchto soustav jinak, na rozdíl od plochého. Zakřiveným prostoročasem je také prostoročas popisující náš rozpínající se vesmír. Zde se mimochodem nedejme zmýlit terminologií, často se dá narazit na zmínky, že náš vesmír je plochý – ona je to pravda pokud se bavíme o prostorové části metriky, pokud se ale bavíme o celém prostoročase, tedy nejen o jeho prostorové části, tak plochý není. Proto v našem vesmíru opravdu existuje (v každém jeho bodě) význačná soustava – je to soustava, vůči níž se velmi vzdálené galaxie vzdalují stejně rychle (samozřejmě musíme porovnávat rychlost stejně vzdálených galaxií, protože rychlost jejich vzdalování roste se vzdáleností). Pokud bychom přešli do soustavy velice rychle se pohybující vůči té předchozí, tak takovou soustavu velice snadno poznáme, protože v jednom směru se stejně vzdálené galaxie budou vzdalovat větší rychlostí (tedy budou mít větší rudé posuny) než ve směru opačném.
Jinými slovy, i pokud se nevydáváme do zrádného mikrosvěta a zůstáváme v bezpečí makroskopických jevů popisovaných obecnou teorií relativity, tak ani tehdy nemůžeme říct, že žádná význačná soustava neexistuje – ona existuje, v každém bodě vesmíru je to totiž ta soustava, ve které platí Hubbleův zákon, který praví, že vzdálené galaxie se od nás vzdalují rychlostí v=H*d, kde H je Hubbleova konstanta a d je vzdálenost galaxie. Nevýznačné soustavy naopak poznáme podle toho, že v nich Hubbleův zákon neplatí (ve skutečnosti se ale vůči té význačné soustavě musíme pohybovat docela velkou rychlostí, abychom poznali rozdíl, Hubbleův zákon totiž platí statisticky, protože kromě Hubbleova vzdalování vykazují galaxie také svůj vlastní pohyb, takže Hubbleův zákon vyjde najevo až po vystředování těch vlastních pohybů).
Dobře, víme tedy, že v každém bodě našeho vesmíru existuje význačná soustava, proč tedy fyzikální zákony mají mít stejnou formu i v těch nevýznačných soustavách? Po pravdě řečeno – nemusely by mít stejnou formu, nicméně výsledky experimentů ukazují, že stejnou formu mají, pokud se pohybujeme jen v tak velkých oblastech prostoročasu, na kterých lze jeho křivost zanedbat. Křivost prostoročasu (tu globální) lze s velkou přesností zanedbat až do oblastí o velikosti řádově deset miliónů světelných let. Skutečnost, že zákony speciální teorie relativity až do oblastí těchto velikostí platí, a že z jejich pohledu žádná význačná soustava neexistuje (což jako první naznačily výsledky Michelsonova-Morleyova experimentu), můžeme chápat jako docela zajímavý experimentální fakt, kdy ačkoliv globálně význačná soustava existuje, tak lokálně žádná taková zjistit nejde, a to ani měřením rychlosti světla (které se ve všech lokálních vůči sobě se pohybujících inerciálních soustavách pohybuje stejně rychle), ani zjišťováním tvaru fyzikálních zákonů (které opět ve všech lokálních vůči sobě se pohybujících inerciálních soustavách mají stejnou formu).
Nyní se pokusme v myšlenkách přenést do extrémně malých škál, např. na úroveň oné Planckovy škály. Pokud jsou očekávání ohledně kvantové gravitace oprávněná, tak na těchto škálách by mělo docházet k velkým fluktuacím gravitačního pole, a tím i geometrie prostoročasu. Prostoročas, který se na vyšších škálách jeví jako velice hladký a plochý, bude mít pravděpodobně na Planckově škále velice divokou geometrii. Situace by mohla připomínat hladinu jezera za velice lehkého vánku – zatímco při pohledu z dálky vypadá naprosto rovná, při blízkém pohledu uvidíme velké množství maličkých vlnek. Podobně v případě prostoročasu na Planckově škále očekáváme množství lokálních zakřivení, nebo dokonce spontánní vznik a zánik mikroskopických černých či dokonce červích děr. Jinými slovy, sice dnes stále ještě nevíme, co můžeme na Planckově škále očekávat, dá se pouze říct, že jediné, co tam naopak neočekáváme, je hladký a plochý prostoročas.
No a nyní se dostáváme opět k tomu, že neexistence význačné soustavy platí jen v plochém prostoročase. Řekli jsme si už, že v případě globálního rozpínajícího se vesmíru v každém bodě vesmíru význačnou soustavu máme, poznáme ji podle toho, že v ní platí Hubbleův zákon ve tvaru v=H*d. Naopak na obrovském rozpětí škál od cca deseti miliónů světelných let až do několik řádů nad Planckovou škálou lze prostoročas považovat za plochý, tím pádem význačná soustava zde nemá žádné opodstatnění – výsledky experimentů navíc opravdu ukazují, že na těchto škálách speciální teorie relativity naprosto excelentně popisuje děje zde probíhající (odhlédneme-li od lokálních zakřivení prostoročasu např. v blízkostech neutronových hvězd či černých děr). Pokud se ale vypravíme ještě níže, dostáváme se do oblasti, kde sice nevíme, jak to tam bude vypadat, ale očekáváme veliké fluktuace geometrie prostoročasu. V takovém případě se docela dobře opět může vynořit nějaká význačná soustava, v níž bude tento mikroskopicky pokroucený prostoročas vypadat statisticky jinak, než v soustavách vůči té význačné se pohybujících.
A to je právě ta otázka, jestli na těch Planckových škálách ta význačná soustava existovat bude, nebo jestli bude i na této úrovni vypadat prostoročas ve všech soustavách v průměru stejně. Právě tuto otázku zodpovídají různé kvantové teorie gravitace různě. A my si dnes můžeme pouze hodit korunou, která z těch dvou možností se nakonec ukáže ta správná, protože tuto otázku se s největší pravděpodobností do konce tohoto století zodpovědět nepodaří. Pokud se nakonec ukáže, že žádná význačná soustava ani na Planckově či jiné fundamentální škále neexistuje, tak potom není důvod ani na takto malých škálách předpokládat narušení Lorentzovy invariance a tudíž ani CPT symetrie. Pokud se ale ukáže, že na takto malých škálách význačná soustava existuje, tak potom na nich Lorentozva invariance i CPT symetrie budou narušeny.
Re: Je Planckova délka správnou škálou
Karel Petr,2017-02-06 10:31:22
Díky za zajímavý příspěvek do diskuse. Měl bych k jedné jeho pasáži dotaz. Některá astrofyzikální pozorování vzbudila před pár lety pochybnosti o tom, zda je Planckova délka správnou škálou pro kvantovou zrnitost časoprostoru. Podle nich by k ní mělo docházet v rozměrech o několik řádů menších; vizte např. https://www.sciencedaily.com/releases/2011/06/110630111540.htm nebo https://phys.org/news/2012-01-physics-team-constraints-lumpy-space-time.html. Nastal od té doby nějaký posun (vyvrácení, podpora dalšími indiciemi)? Jsou nějaké silné teoretické důvody pro to, že za typický rozměr, na kterém se kvantové fluktuace gravitace začnou projevovat, "se dnes všeobecně považuje tzv. Planckova délka" (abych citoval)?
Re: Re: Je Planckova délka správnou škálou
Pavel Brož,2017-02-07 00:38:08
Takhle, ty teoretické důvody jsou pouze založeny na víře, že když máme nějaké veličiny, ze kterých se dá jednoznačně zkonstruovat veličina požadované fyzikální dimenze (např. délky, času, hmotnosti, atd.), tak tato veličina pak hraje roli příslušné škály pro jevy, které by měly být podmíněny pouze příslušnými vstupními veličinami. Protože to v této obecné formulaci nezní ani trochu pochopitelně, lepší to bude ilustrovat na příkladech, kdy to zhruba funguje. Dejme tomu, že vůbec neznáme, a to ani řádově, poloměr nejmenšího atomu, atomu vodíku, a chceme si udělat nějakou hrubou představu, jak by tak zhruba asi mohl být velký. Dejme tomu, že známe velikost Planckovy konstantu h_bar (zhruba 10^-34 kg m^2 s^-1), známe hmotnost elektronu m (cca 0,9*10^-30 kg), známe velikost veličiny e^2/(4 pi epsilon0) (zhruba 2,3*10^-28 kg m^3 s^-2), kde e je náboj elektronu a epsilon0 permitivita vakua. Předpokládáme dále, že velikost nejmenšího atomu by měla být určena zejména Coulombickou přitažlivou silou mezi elektronem a protonem, která je rovna -e^2/(4 pi epsilon0 r^2), dále by měla záviset na Planckově konstantě, pokud tedy předpokládáme, že elektronový obal atomu je primárně kvantový jev, a taky předpokládáme, že by měl záviset na hmotnosti elektronu, protože v analogii s klasickou fyzikou očekáváme, že přitažlivá síla by měla být v rovnováze se silou odstředivou, a ta je úměrná hmotnosti elektronu. Velikost atomu vodíku ve skutečnosti plyne ze Schrödingerovy rovnice, v níž opravdu tyto tři veličiny vystupují – Planckova konstanta h_bar, veličina e^2/(4 pi epsilon0) i hmotnost elektronu m. My ale dejme tomu neznáme, jakou rovnicí se přesně daný fenomén řídí, pouze jenom předpokládáme, že příslušná rovnice závisí na zmíněných konstantách, a proto předpokládáme, že řešení bude taky záviset na těchto konstantách. Plus budeme předpokládat, že příroda nebude vyloženě zlomyslná, a že v řešení nebudou figurovat velké bezrozměrné konstanty.
Ze zadaných konstant h_bar, e^2/(4 pi epsilon0) a m lze zkonstruovat veličinu rozměru délky pouze takto:
r = (bezrozměrný faktor) * 4 pi epsilon0 h_bar^2 / e^2 m
Opravdu, můžeme se přesvědčit, že veličinu o rozměru délky ze zadaných tří konstant žádným jiným způsobem nesestrojíme. Neznáme pouze velikost onoho bezrozměrného faktoru – a právě zde spoléháme na to, že příroda „nebude zlomyslná“, tzn. doufáme, že tento faktor nebude ani extrémně velký, ani extrémně malý – v ideálním případě by mohl být kombinací malých celých čísel a event. čísla pi, které velice často v rovnicích vychází, i tam, kde ho vůbec nečekáme. Tento faktor ale i tak klidně ovlivnit výsledek v rozsahu plus minus jeden řád nebo i plus minus dva řády – tak např. pokud tento faktor bude 4 pi (zhruba 12,56), tak to už máme jeden řád navíc, a klidně může být i umocněn na druhou, a pak jsme hned o dva řády vedle.
Konkrétně v případě velikosti atomu vodíku nás právě popsaná rozměrová analýza opravdu dovede ke správné hodnotě velikosti atomu vodíku, která je určena tzv. Bohrovým poloměrem:
a0 = 4 pi epsilon0 h_bar^2 / e^2 m = 0,5 * 10^-10 m
Jinými slovy, na to, jak jsme vařili z vody, za předpokladu, že neznáme rovnici určující daný fenomén, pouze jsme znali dílčí konstanty, které velikost daného jevu měly určovat a doufali v „nezlomyslnost přírody“, tedy v to, že v řešení nebudou figurovat ani příliš velké, ani příliš malé bezrozměrné faktory, tak čistě jen na základě rozměrové analýzy (kde rozměrem je zde chápán rozměr fyzikální jednotky, např. hmotnost, energie, délka, čas) jsme dospěli k velice slušnému odhadu velikosti daného fenoménu.
Podobně se nám podaří uspět např. v případě hledání škály typické pro relativistické kvantové elektrodynamické děje (tj. při hledání škály, na níž začínají hrát roli efekty kvantové elektrodynamiky, jako je třeba anihilace a kreace elektron-pozitronových párů) či při hledání velikosti gravitačního poloměru černých děr. V prvém případě očekáváme, že příslušná škála bude záviset na rychlosti světla c (jelikož se má jednak o jevy relativistické, tj. při rychlostech srovnatelných s rychlostí světla), dále očekáváme závislost na klidové hmotnosti elektronu m (kvantová elektrodynamika je teorií fotonů, elektronů a pozitronů – pokud bychom ale chtěli místo elektronů a pozitronů pracovat s protony a antiprotony, také to jde, musíme ale vzít zase jejich klidovou hmotnost), a dále očekáváme závislost na Planckově konstantě h_bar, protože nás zajímají děje kvantové. Dá se ukázat, že z těchto tří konstant c, m a h_bar můžeme zkonstruovat veličinu rozměru délky pouze takto:
(bezrozměrný faktor) * h_bar / m c
Pokud ignorujeme bezrozměrný faktor, tak opravdu dostaneme tzv. Comptonovu vlnovou délku elektronu, která charakterizuje příslušnou škálu:
lambda = h_bar / m c = 3,86*10^-13 m
Podobně zase z rychlosti světla c, gravitační konstanty G a hmotnosti tělesa M můžeme zkonstruovat velikost příslušné škály takto:
(bezrozměrný faktor) * G M / c^2
Pokud za bezrozměrný faktor vezmeme číslo 2, dostaneme přesně Schwarzschildův gravitační poloměr:
r_g = 2 G M / c^2
Proč by v této škále měly figurovat právě zmíněné konstanty? Protože gravitační poloměr tělesa hmotnosti M (tj. poloměr černé díry hmotnosti M) by měla být vzdálenost, na které hrají významnou roli relativistické jevy (konstanta c) i gravitace (gravitační konstanta G). Tedy i v případě gravitačního poloměru uspějeme s naší taktikou hledat příslušnou škálu ve tvaru výrazu zkonstruovaného z několika vstupních veličin, které mají daný fenomén charakterizovat.
Naprosto stejným způsobem je odůvodněna víra v to, že kvantově gravitační jevy se projevují na škále blízké k Planckově délce. Pokud se totiž pokoušíme najít typickou škálu, na které hrají roli jak relativistické děje (konstanta c), tak gravitační děje (gravitační konstanta G), tak kvantové děje (Planckova konstanta h_bar), pak jediný způsob, jak zkonstruovat veličinu rozměru délky je tento:
(bezrozměrný faktor) * odm (h_bar G / c^3)
Opět, pokud ignorujeme bezrozměrný faktor, dostaneme veličinu, kterou nazýváme Planckovou délkou:
L_p = odm (h_bar G / c^3) = 1,6*10^-35 m
I tuto veličinu jsme mohli zkonstruovat bez znalosti příslušné rovnice, pouze na základě rozměrové analýzy jakožto výraz zkonstruovaný z konstant, které mají být pro danou škálu charakteristické. Oproti třem předchozím příkladům je zde ale důležitý rozdíl – v případě Bohrova poloměru, Comptonovy vlnové délky i gravitačního poloměru my známe příslušné rovnice, a příslušné škály z nich umíme vypočíst – těmito rovnicemi jsou postupně Schrödingerova rovnice pro elektron v Coulombickém poli protonu, Diracova rovnice pro elektron, a Einsteinovy rovnice pro statické sféricky symetrické pole. Z těchto rovnic umíme příslušné škály vypočíst, a můžeme tak ověřit, nakolik přesně jsme se s naší rozměrovou analýzou trefili do správného výsledku. Ve zmíněných třech případech jsme se trefili přímo excelentně, pro Bohrův poloměr i Comptonovu vlnovou délku jsme se trefili včetně bezrozměrného faktoru (jinými slovy, bezrozměrný faktor ve správných výsledcích byl 1), a u gravitačního poloměru jsme pouze museli doplnit bezrozměrný faktor 2.
V případě typické škály pro kvantově-gravitační děje ale dodnes žádnou experimentálně otestovanou rovnici nemáme, resp. máme hodně teorií, ale nevíme, která je správná, která tedy nabízí tu správnou rovnici. Proto dodnes netušíme, jak velký bezrozměrný faktor u toho výrazu odm (h_bar G / c^3) může být. Jak už jsem zmínil, z rovnic se může velice snadno vylíhnout faktor typu 4 pi nebo 1/(32 pi^2) nebo libovolný podobný. Proto dnes vůbec nemá žádný smysl bazírovat na tom, jestli se kvantově gravitační jevy projeví na Planckově škále, nebo dva řády nad ní či naopak dva řády pod ní. Bude-li příroda „zlomyslná“, může těch řádů mimo být i více.
Zatím jsme si ukázali tři příklady, kdy rozměrová analýza vede k velice uspokojivým odhadům v případě odhadu velikosti atomu, odhadu škály pro kvantově-elektrodynamické děje a odhadu velikosti černé díry. Ukažme si nyní pro změnu příklad, kdy rozměrová analýza totálně selže – tímto příkladem jsou hmotnosti známých elementárních částic.
Proveďme formálně analogické úvahy, jako výše. Předpokládejme, že hmotnosti elementárních částic vyplývají jako řešení nějaké fundamentální rovnice, kterou dnes ještě neznáme. Předpokládejme, že tato rovnice popisuje sjednocení všech interakcí včetně gravitace, takže určitě v ní bude vystupovat gravitační konstanta G, dále rychlost světla c (jelikož půjde dozajista o rovnici relativistickou), a dále Planckova konstanta h_bar (jelikož půjde o kvantově-polní rovnici). Budeme se snažit z těchto tří veličin zkonstruovat veličinu jednotky hmotnosti. Snadno zjistíme, že jediný způsob, jak takovou veličinu sestavit, je tento:
(bezrozměrný faktor) * odm (h_bar c / G)
Pokud ignorujeme bezrozměrný faktor, dostaneme tzv. Planckovu hmotnost:
m_p = odm (h_bar c / G) = 2,17 * 10^-8 kg
A zde je problém – tato veličina je o téměř 17 řádů větší, než nejtěžší známá elementární částice, kterou je to kvark, a o 22 řádů větší, než je hmotnost elektronu. Takže v tomto případě nejde jen o plus minus řád, ani o plus minus dva řády, ale jsme o 17 až 22 řádů mimo (a pokud bychom brali v potaz neutrino s klidovou hmotou řádově stotisíckrát menší než elektron, tak dokonce až o 27 řádů mimo).
Čím je to způsobeno, že hmotnosti částic jsou o tolik řádů menší, než typická hmotnostní škála zkonstruovaná z fundamentálních konstant h_bar, c a G? To dodnes nikdo neví, dodnes je to záhada.
Takže vidíme, že předpoklad, že kvantově–gravitační děje se začínají projevovat na škále cca 10^-35 m (tedy na Planckově škále) je předpokladem postaveným pouze na víře, že příroda nebude v tomto konkrétním případě zlomyslná, a že příslušný dnes neznámý bezrozměrný faktor, který vyplyne z finálních rovnic, které dnes ještě s jistotou neznámé, nám tuto škálu neodsune o příliš hodně řádů mimo.
Nyní se ještě krátce zmíním o těch odkazech, které jste uvedl. Na rovinu musím říct, že novinky ve fyzice nesleduji, takže i když jsem svého času zaznamenal tuto zprávu, ty prameny jsem si prostudoval až dnes. Uvedl jste tyto dva odkazy:
https://www.sciencedaily.com/releases/2011/06/110630111540.htm
https://phys.org/news/2012-01-physics-team-constraints-lumpy-space-time.html
K prvnímu z nich jsem na archivu (arxiv.org) dohledal veřejně přístupnou verzi, ta je zde:
https://arxiv.org/pdf/1106.1068.pdf
Ke druhému jsem bohužel dohledal pouze placené verze, takže u toho druhého Vašeho odkazu mohu vycházet pouze z toho, co je uvedeno v tom popularizačním článku, a z toho se moc usoudit nedá. V případě toho prvého se ale dá říct o mnoho více, proto se zmíním především o něm.
Článek https://arxiv.org/pdf/1106.1068.pdf popisuje omezení velikostí několika typických členů v Lagrangiánu, které mohou být uvažovány jako potenciální možná narušení Lorentzovy symetrie. Takových možných narušujících členů může sice existovat nekonečně hodně, nicméně dají se seřadit podle jakýchsi „mocnin účinku“ – jinými slovy, členy s nízkými mocninami se projeví sice dříve, jejich efekty budou ale se zmenšující se délkovou škálou narůstat pomaleji, oproti tomu ty členy s vyššími mocninami budou narůstat rychleji, projeví se ale později, a případně jen v některých speciálních jevech. Tyto narušující členy způsobují různé efekty, které jsou spjaté s narušením Lorentzovy invariance – např. tzv. dvojlom vakua (kdy se různé polarizace světla šíří různými rychlostmi) nebo disperzí světla ve vakuu (kdy různé vlnové délky mají putovat vakuem různou rychlostí). Zmíněnými mocninami se přitom nemyslí skutečné mocniny těch členů, ale jejich tzv. dimenze, přesněji řečeno, rozměr odpovídající fyzikální jednotky. Článek rozebírá jeden konkrétní narušující člen dimenze 5, a obecně pojednává o možných výsledcích pro podobné členy dimenze 6, a teoretické vývody konfrontuje s experimentálními daty sesbíranými při sledování gama výtrysku s označením GRB041219A. Jednalo se tedy o gama výtrysk ze dne 19.12.2004. Tento gama výtrysk byl zaregistrován družicí Integral, pocházel ze zdroje vzdáleného 277 miliónů světelných let, a obsahoval fotony o energiích od 200 do 325 kEV (tedy gama záření).
Studium vzdálených gama záblesků je přímo ideální pro odhalování jevů jako je dvojlom vakua nebo disperze světla, protože tyto efekty se kumulují během putování fotonů od zdroje k nám. Na základě studia polarizace detekovaného světla a studia případného zpoždění vysokoenergetické složky vůči té méně energetické pak lze dospět k omezením kladeným na velikost příslušných narušujících členů (přesněji řečeno, na velikost bezrozměrných konstant u těchto členů). Rozborem dat pro výsledky získané pro v článku studované operátory dimenze 5 a 6 se omezení na tyto bezrozměrné konstanty podařilo najít, v případě operátoru s dimenzí 5 šlo o výrazné zpřesnění oproti výsledkům z dřívějších gama záblesků. Nicméně tyto výsledky naprosto nic neříkají o velikosti škály, na které se začínají projevovat kvantově-gravitační efekty – tyto výsledky hovoří jen a pouze o omezení na velikost příslušných narušujících členů. Mezi velikostí škály typické pro kvantovou gravitaci a mezi velikostí členů narušujících Lorentzovskou invarianci přitom není žádný přímočarý vztah – opět, museli bychom disponovat kompletní teorií kvantové gravitace, abychom takový vztah našli. Takže ten první článek rozhodně nic nevypovídá o velikosti škály pro kvantově-gravitační děje, vypovídá jen a pouze o limitujícím omezení pro několik vybraných členů, které Lorentzovskou invarianci narušit mohou.
Druhý článek, jak už jsem zmínil, mohu hodnotit pouze z jeho popularizační verze, ve které se opravdu hovoří o tom, že kvantově gravitační jevy by se mohly odsunout až na škálu 500 krát menší, než je Planckova škála. Opět má jít o omezení vyplývající ze studia dat z gama záblesků. Bohužel zde naprosto netuším, a jakým modelem autor pracuje, to v tom popularizačním článku není. Mohu pouze říct, že jeho závěr musí být nutně modelově podmíněný. Jak už jsem zmínil, můžeme dnes studovat potenciální projevy různých členů narušujících Lorentzovskou invarianci – tvar těchto členů je znám, a i když je jich celkově nekonečně mnoho, dají se seřadit do jakési posloupnosti podle „účinku“. Můžeme dnes na základě studia gama záblesků získávat různá omezení pro velikost těch či oněch členů. To, co ale dnes s jistotou neznáme, je teorie popisující kvantovou gravitaci. Různé teorie diktují různě velké bezrozměrné konstanty u těchto členů. Studiem gama záblesků tedy můžeme už dnes tu či jinou teorii vyvrátit, pokud pro příslušnou konstantu získáme z pozorovaných dat menší hodnotu, než jakou požaduje teorie. Nelze ale učinit závěr o tom, kde je typická škála pro kvantově gravitační děje. Už jenom z toho důvodu ne, že interakce fotonů s gravitačními fluktuacemi nemusí být tou správnou reprezentativní oblastí pro kvantově-gravitační fenomény – jinými slovy, nikde není řečeno, že na kvantově-gravitační efekty nenarazíme mnohem dříve s jinými částicemi, než s fotony.
Jinak co se týče Vaší otázky, jestli se od té doby nic v této oblasti nezměnilo, tak se znovu omlouvám, novinky bohužel nesleduji, resp. maximálně občas a zpětně, takže nic novějšího Vám k tomuto tématu neřeknu.
Porušení symetrie u rozpadů
Honza Skácel,2017-02-05 14:18:50
Upřímně jsem čekal (a těšil se) na komentář k prvním experimentálním pozorování rozdílů u rozpadů baryonové hmoty http://www.nature.com/nphys/journal/vaop/ncurrent/full/nphys4021.html
Re: Porušení symetrie u rozpadů
Vladimír Wagner,2017-02-05 15:18:13
Tohle je trochu mimo téma tohoto článku. Mám rozepsaný přehled výsledků LHC (do března teď má zimní přestávku) za dva roky a tam mám o měření LHCb v oblastí narušení CP symetrie část, která se věnuje i tomuto výsledku. Nyní bych tedy uvedl jen pár důležitých bodů. Pozorování rozpadů baryonu lambda b na proton, pi mezon a dva kaony nebo na proton a tři pi mezony je velmi cenný úlovek. Tento baryon se dominantě rozpadá na nabitý baryon lambda c a leptony. Nyní pozorované rozpady se vznikem protonu jsou velmi vzácné a citlivé na narušení CP-symetrie. Ta ovšem je běžně pozorovaná, i když zatím jen v rozpadech mezonů, a je obsažena ve standardním modelu. Pozorované narušení CP symetrie v mezonovém sektoru zatím plně odpovídá standardnímu modelu. Pokud se pozorování narušení CP symetrie v rozpadu lambda b na proton a tři mezony pi potvrdí (zatím je to na úrovní tři sigma, to není zase tak moc průkazné), bude hodně záviset, jestli bude odpovídat standardnímu modelu nebo ne. Pokud ano, tak je to zajímavé měření, které bylo malou pravděpodobností tohoto rozpadu a malou intenzitou narušení výzvou, ale jinak nic zlomového. Jiná věc by byla, kdyby velikost efektu byla jiná než odpovídá standardnímu modelu, pak by to byla známka nové fyziky a opravdu zajímavý průlom. Zatím však k rozhodnutí této věci máme dost daleko.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce






