Tento článek bude krátký, protože odpověď je poměrně jednoduchá. Stačí se podívat na nepřímé ukazatele teplot. Jiné ukazatele, které nejsou v ohnisku všeobecné pozornosti. Takovým opomíjeným ukazatelem je tempo růstu CO2 v atmosféře. Použijeme ho jako rozhodčího v našem sporu.
O tomto indikátoru se moc nemluví. Protože podle politicky korektních dogmat CO2 řídí teplotu a nikdy naopak. Jenže ve skutečnosti meziroční tempo růstu CO2 v atmosféře závisí na teplotě oceánu. Podle toho se mění rozpustnost CO2 ve vodě. Takže po horkém roce následuje velký přírůstek CO2 v atmosféře.
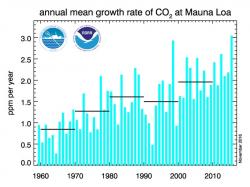
Podíváte-li se na graf 2, vidíte, že v roce 2015 v atmosféře přibylo 3,05 ppm oxidu uhličitého, což je jen nepatrně více než v horkém roce 1998, kdy přibylo 2,93 ppm. Vzhledem k nepřesnostem měření je to prakticky identické. Ponechme stranou, že 30 let nákladných klimatických konferencí a dotací tempo růstu CO2 zjevně nijak nesnížilo. Pro nás je důležité, že to odpovídá teplotním údajům ze satelitů. Ty říkají totéž. Rok 2015 byl nepatrně, ale jen nepatrně teplejší než rekordní rok 1998.
Závěr? Satelitní měření teplot je zřejmě správné. Pozemní měření NASA (graf GISSTEMP) se přehřívá v důsledku chyby. Doufejme, že nová americká vláda tuto věc bude s vedením této své agentury řešit. Jinak vědecká pověst NASA může být vážně poškozená.
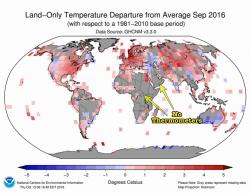
Jak by mohlo dojít k omylu? Co se týče pozemního měření, na Zeměkouli je spousta bílých míst, odkud nejsou data. Nebo tam měřící stanice jsou, ale z nějakého důvodu do výpočtu nejsou zařazené. Hic sunt leones – zde jsou lvi, to se psávalo ve starověku na mapy v místech, kam se kartograf neodvážil. V těchto nezmapovaných lokalitách klimatologové teplotu jen odhadují.
|
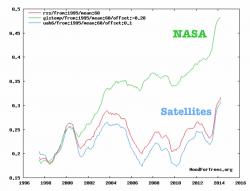
GRAF 1: Modře a červeně je globální průměrná teplota podle údajů satelitů. Zeleně je globální průměrná teplota podle autorů z NASA, na základě vybraných pozemních stanic. Kdo má pravdu? |
|
|
GRAF 2: Tempo ročního růstu CO2 v atmosféře. Některý rok přibude 2 ppm ročně a jindy třeba 2,5 ppm. Závisí to na teplotě oceánu v předchozích měsících. |
|
|
GRAF 3: V šedých oblastech nejsou žádná měření. Nebo autor mapy místní teploměry ignoroval a nezapočetl je. |
|
|
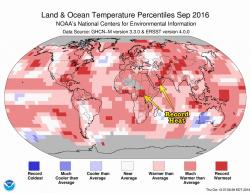
GRAF 4: Klimatolog ale zaplní mapu svými odhady. A v místech, odkud žádná měření nejsou, se rozhodne odhadnout rekordní teplo. |
|
|
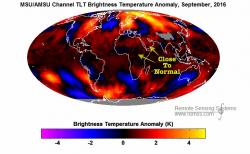
GRAF 5: Satelitní snímky téměř žádné mezery ani bílá místa nemají. Rekordní horko nepotvrzují. |
ZDROJE:
http://realclimatescience.com/2016/11/why-does-the-us-space-agency-ignore-satellites/
https://www.co2.earth/co2-acceleration
http://www.esrl.noaa.gov/gmd/ccgg/trends/gr.html
http://www.drroyspencer.com/latest-global-temperatures/
http://realclimatescience.com/2016/11/noaa-september-temperature-fraud/
Zastaví lidstvo nadcházející dobu ledovou?
Autor: Stanislav Mihulka (19.01.2016)
Klimatologům vadí, že polární mořský led odmítá roztát
Autor: Vítězslav Kremlík (29.04.2016)
Umělé mraky globální oteplení poněkud zchladily
Autor: Josef Pazdera (31.05.2016)
Klimatický panel varuje před „novým druhem“ skepticismu
Autor: Vítězslav Kremlík (22.08.2016)
Jihovýchodní Afrika nevysychá, vlhne
Autor: Josef Pazdera (23.10.2016)
Diskuze:
Satelity
Stanislav Florian,2016-11-30 11:04:04
Diskuze k obdobnému článku V. Kremlíka na neviditelnypes.cz
http://neviditelnypes.lidovky.cz/diskuse.aspx?iddiskuse=A161129_151948_p_klima_wag
Pan Šejna říká, že satelity neměří teplotu 2 m nad zemí
".. uvádím globální teplotní trendy jednotlivých měření:
+0,174 °C za dekádu ... pozemní meteorologická měření - teplotní řada NASA
+0,135 °C za dekádu ... satelitní měření RSS - kanál TLT (výška 0 až 10 km)
-0,260 °C za dekádu ... satelitní měření RSS - kanál TLS (výška 10 až 27 km)
-0,760 °C za dekádu ... satelitní měření RSS - kanál C14 (výška 27 až 50 km)
http://images.remss.com/msu/msu_time_series.html
trend satelitních dat od 1980
http://images.remss.com/msu/msu_data_monthly.html
Proč se otepluje
Martin Jahoda,2016-11-26 09:54:45
https://cs.wikipedia.org/wiki/Doba_ledov%C3%A1 - třeba zde si může každý zjistit, že ledovce tají a teplota stoupá už více jak 20000 let. To, že si toho v posledních 50 letech všimli někteří chytráci a udělali si z toho byznys je úplně něco jiného a svědčí to s píš o tom, že lidem se dá nakecat cokoliv, když jste dobrý řečník. Ostatně kriminalisté a psychologové vědí své....
Jen pro shrnutí:
1) Před více jak 20000 lety byla poslední velká doba ledová.
2) Země byla pokrytá ledem - vznikly ledovce na kterých se tak bezva lyžuje.
3) Od této doby se otepluje a tají ledovce - čím jsou menší tím zdánlivě tají rychleji.
4) Po 20000 letech člověk vymyslel, že teplo je špatně a že za to může CO2.
5) Ale CO2 je důležité pro život - všechny rostliny na suchu i ve vodě spracovávají CO2 a získávají tak uhlík pro stavbu svých těl.
6) Rostliny jsou pak potravou živočichů a ti dalších živočichů a tak CO2 mizí z atmosféry a mnění se na život.
7) Nejhorší věc, kterou člověk dělá není pálení uhlí a ropy ale biomasy. Biomasa by se měla stát potravou a přemněnit se na další živočichy, kteří se pak částečně stanou opět potravou a částečně se uloží pod povrch a na dna oceánů, kde je překryjí sedimenty.
Závěr:
Celé oteplování je především byznys. S vědou to má společného málo. Al Gore má miliardové příjmy z prodeje odpustků. Pokud někdo příjde ve vědeckých kruzích s výzkumem, kter by to spochybnil je okamžitě vyhnán a jsou mu odpírána možnost vědecky pracovat - stejně jako za středověku církev nedovolovala jiný výklad vesmíru se dnes "nedoporučuje" to samé v klimatologii. Přitom se ví a i každý sedlák to zná, že největší vliv na teplotu má oblačnost, ale nikdo to nezkoumá. Byli dělány návrhy, že by se udělal výzkum ale nikdo na to nedostal peníze... Proč asi...
Re: Proč se otepluje
Martin Jahoda,2016-11-26 10:10:54
Omlouvám se za překlepy a pár chyb...
Jen ještě dovysvětlení. Dříve se biomasa stávala potravou pro dobytek a člověka nebo surovinou pro zpracování třeba na nábytek a věci kolem nás. Z ropy se dělaly plastové výrobky. A tak CO2, které bylo v atmosféře se zase přirozeně zpracovávalo a ropa se neměnila jen na CO2 jak tvrdí greenpeace ale na trvalé výrobky...
Dnes se snižuje výroba masa, biomasa se pálí a plasty jsou zlo. Přitom plasty vydrží několik set let nž se rozpadnou a uchovají v sobě uhlík - pokud je někdo neprožene spalovnou. Tady můžete vidět jak je celá ekologie postavena na pocitech a né na seriozních faktech. To co se jeví jako ochrana přírody jí může škodit a způsobit třeba hladomor, nebo vymírání druhů a naopak.
Re: Proč se otepluje
Stanislav Florian,2016-11-26 13:30:44
Nejde jen o to, že se otepluje, ale že se vlivem emisí otepluje rychle až nejrychleji. Obilné pásy s úrodnou půdou nikdo nepřesune a budou mít málo vody.
Zvýšená teplota má vliv na oblačnost, více oblačnosti ---> ochlazení větším odrazem slunečního záření do vesmíru.
Spalování biomasy vrací CO2 do oběhu rychleji než přirozené vázání zpět, ale nevrací minerály, které odtečou odpadní vodou, místo toho aby zůstaly v půdě a spolu s organickými zbytky vázaly živiny a vodu jako humus plný mikroskopického života. Spalování biomasy = degradace půdy.
Je hezké, že spálením biomasy jsme vrátili do přírody CO2 ze 100-letého stromu, ale nový místo něj poroste celých 100 let, takže za 50 let se vrátí do dřeva sotva polovina.
V roce 2050 bude třeba o 70% více potravin. A našich polí budou pískoviště.
Re: Re: Proč se otepluje
Martin Jahoda,2016-11-27 09:36:06
Neotepluje se rchleji. To jsou jen normální výkyvy. Navíc se posledních 15 let teplota nemnění a to přes neustálé ohlašování teplotních rekordů. Přímo úsměvně pak působilo oznámení IPCC v roce 2015, že pokrytí ledem v arktidě dosáhlo nejmenší plochy v měřené historii. Pravda byla, že na snímcích z družice bylo o 40% větí než bylo to skutečně nejmenší Kdybyste žil v letech 1965-1980 tak byste zjistil, že se stejně rychle ochlazovalo a mluvilo se o přípravě na dobu ledovou. Strašení pouští a podobně je známá taktika IPCC. Vyvolat strach, označit nepřítele a pak zdanit nebo vymyslet technologii z nutností dotací a ty se pak přerozdělí mezi vyvolené firmy......
Re: Re: Re: Proč se otepluje
Milan Krnic,2016-11-28 18:45:43
Hlavně co se týče přeměny krajiny v poušť, beru za zřejmé, že to je ovlivněno stavem vegetace.
K tomuto pak třeba: http://www.osel.cz/8869-umele-mraky-globalni-otepleni-ponekud-zchladily.html
Plně souhlasím s primárním určením panelu IPCC, ostatně mnoho let se to potvrzuje, a i zde na OSLU je o tom mnoho článků. Navíc co se nyní ukazuje v USA (prohlášení Trumpa), bude díky té bídné klimatické propagandě na jednu stranu pravděpodobně výkyv na stranu druhou (zrušení omezení limitů těžby), zisk se bude generovat dál, a odnese to zase jen příroda.
Re: Re: Proč se otepluje
Milan Krnic,2016-11-28 18:52:02
Já třeba hnojím popelem ze spáleného dřeva. A teď můžete klasicky různě omezit realitu. Třeba jen na mou malinkou zahrádku, která má stále více živin. Anebo jen na les, který má stále méně živin. Anebo dohromady, kdy nula od nuly pojde. Každopádně z mého políčka pískoviště nebude, zatímco v lese, tam bude pláž (jako by se z těch lesů už stovky let netěžilo)
oceánské sondy ARGO
Stanislav Florian,2016-11-25 20:21:24
Obrázek z článku
http://www.osel.cz/popisek.php?popisek=21026&img=graf3.jpeg
ukazuje povrchové stanice a zpochybňuje výpočty pro prázdná místa.
Globální teplota se však určuje ( přímo měří) rovněž z oceánských automatických stanic ARGO, kde to případné na polemizování o městských tepelných ostrovech nevypadá.
https://en.wikipedia.org/wiki/Argo_(oceanography)
mapa těchto stanic v oceánu roku 2016 ukazuje, že je jich (první od 1999) stále v činnosti dost
https://upload.wikimedia.org/wikipedia/commons/thumb/a/a0/2016-04-countries.png/900px-2016-04-countries.png
Vliv Slunce
Josef Šoltes,2016-11-24 16:45:03
Zajímalo by mne, jak se klimatické modely popasovaly s vlivem Slunce? Ostatně je to zdroj energie a jako takový by měl mít na Zemi naprosto zásadní vliv, ne? Pokud se vypočítávají modely pro miliony let dozadu, bere se v úvahu postupné zesilování zářivosti Slunce?
Re: Vliv Slunce
Stanislav Florian,2016-11-25 00:47:27
Záření Slunce roste asi o 10% za miliardu let, tedy 0,01% za milion let, jinak 0,0001 původního. Pro 168 W/m2 dopadající na povrch je to 0,0168 W/m2 změna za 1 milion let, což je zhruba 1/100 antropogenního nárůst od 1775 ( asi 2 W/m2). Kromě toho se Země vzdálí od Slunce za milion let o 150 km, což je miliontina vzdálenosti, tento vliv je ale malý.
Spíš mě překvapuje filosofie článku, která pomocí mapy stanic zpochybňuje pozemská měření celkově určená výpočtem. Satelity měří proniklé tepelné záření povrchu přes atmosféru k nim a hodnoty určené v podstatě fotobuňkou se přepočítávají na teplotu na celý povrch. A tento zjevně laicky neprůhledný výpočet, ten nevadí. Satelity s oblibou létají v širokém pásu nízkých zeměpisných šířek, kde se využívá při startu rotace Země. Polárních satelitů je méně a dá se tam očekávat větší chyba výpočtu. Objevila se i teorie, že elektronická čidla satelitů během roků mírně vyhasínají a nové se kalibrují podle nich.
Frantisek Matecky
,2016-11-22 09:38:20
Přehřívají se údaje NASA v důsledku chyby?
Údaje se přehřívají? Došlo k omylu? Měří NASA stovku let nesmysly?
Kdo takové články čte? OSEL se snaží být populární, ale prakticky je to žumpa jako blesk.cz.
Globalni oteplovani na ČT:
http://www.ceskatelevize.cz/
Re:
Stanislav Florian,2016-11-22 11:14:16
Článek jste četl evidentně Vy. Odhaduji, že dva hlavní autoři Osel.cz nejsou tak fundovaní a stačí jim být v kvalitě článků druzí až třetí za Vašimi články.
Že satelity neměří totéž co pozemní stanice je dáno samotným principem měření, kde u satelitů působí troposféra s stratosféra a měří se vyzařování.
Teplotu celé nižší troposféry totiž pravidelně měří meteorologické balony a jejich údaje od roku 1958 se zpracovávají do globálních průměrů. Srovnáme-li tato dvě navzájem nezávislá měření, téměř dokonale se kryjí. Obě série ukazují jen velmi nepatrné oteplení (0,034 °C za desetiletí u satelitů a 0,029 °C stupně u meteorologických balonů) ve srovnání s oteplováním povrchu (0,17 °C za desetiletí) a zvláště s očekáváním matematických klimatických modelů AOGCM (0,22 °C za desetiletí). Proto nyní většina komentátorů, IPCC i studie americké Národní rady pro výzkum z roku 2000 potvrzují, že mezi trendem zřetelného oteplování povrchu a trendem nepatrného oteplení atmosféry je opravdu nesoulad.
https://en.wikipedia.org/wiki/Satellite_temperature_measurements
https://upload.wikimedia.org/wikipedia/commons/thumb/7/7e/Satellite_Temperatures.png/1200px-Satellite_Temperatures.png
https://www.carbonbrief.org/satellite-measurements-of-the-troposphere-confirm-warming-trend-data-shows
odtud interaktivní graf https://cloud.highcharts.com/show/ixyhej
"Globální pohled :Existují také rozdíly troposférických a povrchových záznamů v tom, jak se zabývají studeného vzduchu ve vysokých zeměpisných šířkách Arktidy a Antarktidy a nízko položenými mraky v subtropech.To znamená, že troposférický záznam nezachycuje rychlejší oteplování v Arktidě, vysvětluje Oldenborgh. Teploty tam rostou nejméně dvakrát tak rychle, jak je celosvětový průměr.Tyto dva protichůdné efekty se navzájem vyruší v troposférickém záznamu. .."
doba ledova
Libor Tomáš,2016-11-21 22:42:05
Pokud vim, zijeme v dobe meziledove a drive, nebo pozdeji doba ledova zase prijde. Jak tohle klimaalarmisti zahrnuli do svych modelu? Predpokladam, ze nijak jinak by prisli o kseft. Porad me vic desi kilometr ledu pod nohama nez pestovani pomerancu.
Re: doba ledova
Radoslav Porizek,2016-11-24 21:54:12
Pises ako by si nepoznal klimaalarmistov, ked predpokladas ze prichadzajucu dobu ladovu zahrnuli do svojich modelov.
Samozrejme, ze nezahrnuli.
Miesto toho vyprodukovali dalsi model, podla ktoreho uz dalsia ladova doba nepride (dalsich 50-tisic az 100-risic rokov) a basta.
Quiz
Josef Hrncirik,2016-11-21 21:04:11
Cca 2W/m2 z GO navíc (tvrdí se to stále) by mělo ohřívat promíchávaný oceán (do cca 700 m hloubky) rychlostí 2,1*10**-3 °C/rok; tj. o prokazatelných cca 0,02°C /10let či zřejmých cca 0,1°C/ 50 let.
Jsou data chaotická, tj. bez trendu, či jen bez růstu?
Nebo se to neprojevuje, protože ke dnu jde vždy voda o stejné teplotě (při mrznutí) vlivem větší hustoty solanky při větším obsahu soli při vymrzání sladkého ledu a teplejší voda se zchladí vždy až k stejnému b. tuhnutí?
Nárůst teploty v atmosféře je špatně viditelný vlivem přirozeného rozptylu a kolísání.
Jsou dlouhodobá spolehlivá měření chodu teploty ve vrtech např. v křemenci (quarcit)?
, který má teplotní difuzivitu 0,28 cm2/s mnohem větší než voda; za rok v něm teplotní změna urazí cca 20 m, za 100 let cca 200 m.
Lze tak získat stabilní a vyhlazená data i bez hokejky, jen s vrtnou soupravou?
Asi jediné na co se lze spolehnout je dlouhodobá stabilita solární konstanty.
Potom by ale nesmírné klimatické změny cyklů dob ledových byly způsobeny jen změnami cirkulací oceánu a atmosféry změnou orientace zemské osy precesí. Přitom by docházelo zřejmě i k cyklickým změnám ppm CO2 asi podstatným a pak k dokonalé restituci.
Je to úplně jinak?
Re: Quiz
Stanislav Florian,2016-11-22 01:19:10
Země už se podle Milankovičových cyklů vzdaluje od Slunce, doba ledová se přiblíží za několik tisíc let. Primární změna slunečního záření na povrch Země způsobí další faktory jako změnu ppm skleníkových plynů, změnu albeda a další.
Dokud ještě diskutovali klimatologové, tak často o radiačním působení, klimatické citlivosti a zpětných vazbách. Takže pouhý převod antropogenních 2W/m2 podle Stefan-Boltzmannova zákona na změnu teploty nestačí.
https://en.wikipedia.org/wiki/Radiative_forcing
https://en.wikipedia.org/wiki/Climate_sensitivity
http://www.meteocentrum.cz/zajimavosti/globalni-oteplovani/globalni-klimaticky-system
https://cs.wikipedia.org/wiki/Milankovi%C4%8Dovy_cykly
Re: Re: Quiz
Josef Hrncirik,2016-11-22 09:16:00
Díky.
Nakoukl jsem na M. cykly a ke svému překvapení jsem zjistil, že excentricita oběhu Země může být až 0,06.
Momentálně je prý 0,0167 a maximum před 100 000 lety prý bylo velmi nízké 0,019.
Podle Keplerových zákonů (intuitivně) asi s rostoucí excentricitou klesá množství energie přijaté průměrně během jednotky času (průměrného oběhu), průměr W/m2 tj. dalo by se říci efektivní solární konstanta, řekněme Kef.
Jakou funkcí excentricity Kef je?
Nejspíš se to dá rychle najít i poměrně snadno vypočítat.
Nějaký fyzikální olympář by to mohl za půl hoďky zintegrovat, nebo najít.
Re: Re: Re: Quiz
Stanislav Florian,2016-11-22 09:43:51
Graf Milankovičových cyklů má i celkové ozáření na 65°N ( čili v blízkosti severního polárního kruhu)
https://upload.wikimedia.org/wikipedia/commons/thumb/5/53/MilankovitchCyclesOrbitandCores.png/800px-MilankovitchCyclesOrbitandCores.png
která ukazuje, že jsme velmi blízko lokálního minima. Graf je prpočítán dopředu i dozadu v tisících rocích, takže jsme v bodě 0.
Doba ledová má nastat, když všechny tři složky Milankovičových cyklů jsou v BLÍZKOSTI minima. Přesně to prakticky nikdy nenastne, jsou to tak trochu cykly Milankovičové.
Kratší časové měřítko nachází Google
http://hledani.gnosis9.net/img/milankovic-doby-ledove.jpg
Diskuze
http://www.osel.cz/6802-je-nejtepleji-cili-nejchladneji-za-vice-jak-10-000-let.html
Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-22 09:59:28
Díky, to mám všsk na stole taky.
Milankovičovi asi došlo víno a průměr z celé zeměkoule už nevypočítal.
Moc daleko od pólu se tedy nedostal.
Zůstává to tedy na nějakém matfyzákovi či olympionikovi.
Určitě to už někde je.
Možná se dá dokázat, že kontraintuitivně dKef/de = 0?
Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-22 11:34:46
Ozáření 65°N je rozhodující pro posouzení možnosti zalednění.
Faktor způsobený excentricitou se spočítá jako poměr v maximu a minimu excetricity. Ozáření ubývá se čtvercem vzdálenosti. Je třeba se popasovat s tím, co je ta excentricita.
http://pardalnet.wz.cz/PDF/37-Globalni-oteplovani-1.dil.pdf
str 6 a dále
" Závěr je, že vlivem excentricity orbitu dráhy dojde asi za 30 000
let k lokálnímu minimu, kdy se ozáření povrchu Země sníží asi o 9 W/m2, což odpovídá
ochlazení asi o -1,8 °C. "
Jde jen o ozáření, které ale má kumulativní účinek ( zpětná vazba, albedo atd.)
Re: Re: Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-22 13:45:53
Díky.
Chybička se vloudila již na s.2 pardalnet...
Vody v atmosféře je jen 1,27.10**16 kg, tudíž dím, že ekv. vrstva by byla jen 24,9 mm vody.
Buď je to překlep, nebo num. chyba, či úvaha příliš rychlá.
(Vysoký obsah vody je jen při vysoké teplotě, tj. jen v nízkých vrstvách), proto je průměrný parc. tlak vody jen 244 Pa (1,83 mmHg), což na 1. pohled sice vyděsí, ale je to pravda.
V závěru se píše Milankovič přidá až +34 W/m2, není jasné zda k 1365 či k čemu, či co je minimum.
(v rozmezí L.P.1200-2000 odhadováno kolísání cca 1 perioda 1362- 1368 W/m2)
Chybí nekompromisní vyjádření Kef na celý oběh.
Otázka na nebeského mechanika.
Jaká je závislost délky roku na e?
Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-22 23:15:56
Trochu jsem si započítal, a poměr pro celoroční irradianci mezi eliptickou a kruhovou drahou mi vyšel 1/odm(1-e^2), kde e je excentricita. Pro malé excentricity je to přibližně 1+0,5*e^2, tzn. že irradiance roste s rostoucí excentricitou.
Zde je nutné ale zmínit pár důležitých věcí - pro zmíněný výpočet jsem použil předpoklad, že se při změně dráhy zachovává velká poloosa. Velká poloosa je totiž adiabatickým invariantem v rámce poruchové teorie v nebeské mechanice, tzn. když změny dráhy Země perturbacemi okolních planet jsou malé - během celé existence naší planety se opravdu reálně dají předpokládat pouze malé změny excentricity, jednoduše se zatím ani neupekla ve stovkách stupních Celsia, ani nezmrzla při teplotách tekutého metanu, dokonce ani nevymetla blízké planety ze sluneční soustavy. Zkrátka díky kontinuitě života na Zemi můžeme říct, že změny excentricity dráhy Země byly malé, a tím můžeme přijmout přiblížení, ve kterém je délka velké poloosy invariantem.
Bohužel ale nevím, jaké maximální mocniny e jsou relavantní v rámci té poruchová teorie (bohužel nejsem expert na nebeskou mechaniku). Tzn. nevím, jestli příspěvky od druhé mocniny e jsou ještě v souladu s daným přiblížením, a tím i s předpokladem konstantnosti velké poloosy, anebo jestli v daném přiblížení jsou relevantní příspěvky maximálně do první mocniny e. Každopádně oběžná doba je určena právě velkou poloosou, proto se oběžná doba Země během malých změn excentricity nemění, což je odpověď na Vaši poslední otázku.
Excentricita dráhy Země je nyní 0,017 a momentálně se snižuje - tzn. dráha Země se momentálně více "kruhovatí" (viz https://en.wikipedia.org/wiki/Milankovitch_cycles). V souladu s mým vzorečkem výše by tedy celková roční irradiance měla klesat, což koresponduje i s grafem, který je pro příštích padesát tisíc let v pdfku odkazovaném panem Florianem, podle nějž momentálně irradiance v důsledku změny excentricity také klesá.
Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-23 01:30:00
Díky za nelehký výpočet
http://edu.techmania.cz/cs/veda-v-pozadi/606
... Numerická excentricita zemské dráhy je 0,017, lineární excentricita je ..vzdálenost Slunce od středu elipsy je téměř 2,5 milionů km.
Země se vzdaluje díky výměně momentu hybnosti od Slunce asi o 15 cm (0,15 m) za rok, tedy 15 km za 100 000 let, což zanedbat v rámci očekávání doby ledové za několik tisíc let lze zanedbat.
http://gnosis9.net/pdf/otepleni-1-dil.pdf
Graf 34 podle Houghtona má změny excentricity včetně velké poloosy, graf 35 podle Salomona má při změnách excentricity velkou poloosu stejnou. Oba jsou uznávaní klimatologové.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-23 12:23:33
On ten výpočet není obtížný, vlastně počítáme integrál přes čas z 1/r^2 přes periodu oběhu. Diferenciál dt rozšíříme omega/omega, kde omega je úhlová rychlost, výraz omega dt=d fi, tj. diferenciál úhlu měřeného z ohniska, tedy integrál přejde na integraci přes úhel od 0 do 2pi z výrazu 1/(r^2 omega). Jmenovatel je ale moment hybnosti (resp. po vynásobení konstantní hmotností Země jím je), ten se zachovává, takže ho lze vytknout před integrál, a dostaneme 2pi/L(e), kde L(e) je ten moment hybnosti závislý na excentricitě dráhy. Zbývá tedy spočíst závislost toho momentu hybnosti na excentricitě. Tam už toho budeme potřebovat trochu více, mj. i jestli tu excentricitu budeme měnit se zachováním velké poloosy či jinak. Ve výsledku se to podělí stejnou veličinou pro nulovou excentricitu, tím se zbavíme nepodstatných konstant, jako je třeba ta hmotnost atd., ostatně stejně nám jde o relativní vliv.
Ta velká poloosa by se prý ale opravdu zachovávat měla. Kdysi jsem na to narazil během debaty se svým kamarádem astronomem, divil jsem se proč by se zachovávat měla, argumentoval jsem, že při takových procesech, jako byla svého času dnes předpokládaná výměna pozice mezi Uranem a Neptunem v důsledku kumulativního vlivu gravitačních perturbací, se velká poloosa jejich drah samozřejmě nezachovala. Odpověděl mi, že nicméně v rámci drobných poruch, kterými se vysvětlují jevy jako je např. standardní část stáčení perihelia (tj. nikoliv ta obecně-relativistická) je velká poloosa opravdu adiabatickým invariantem a zachovává se. Bohužel nejsem expert na nebeskou mechaniku, musel bych to někde dohledat a načíst, a zase až tak moc mě to zase nezajímá :-)
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-23 13:41:14
Astronomům bych věřil, mají svůj svět plný matematiky.
ALE. Planety ( Země a Jupiter jako hlavní vliv) obíhají v rovině ekliptiky a ve stejném směru. Jupiter by tedy měl působit na zemi jako na družici při efektu gravitačního praku. Rychleji obíhající Zemi přitahuje, pak ji táhne jakoby sebou kousek po své dráze, tím ji dodá energii, pak Země se vzdaluje a ztrácí stejné množství energie jako nabrala při přiblížení. Efekt tedy je, že získává energii z oběžné energie Jupitera. Více energie na dráze Země = větší průměrné parametry dráhy, perihelium i afélium.
Asi to tak bude, ale otázka je, zda to má hodnoty, které něco reálně ovlivní.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-23 13:49:57
Díky, nejsem ani mechanik.
Mám pocit, že perturbant mění hybnost perturbovaného a změny hybnosti jsou opačné.
To už ale neplatí pro změny momentů hybnosti při různých r.
Při různých m jsou různé i změny energie perturbačně interagujících.
Proto jsem ve fázi fascinace, že by tam mohl být nějaký invariant.
Pochopitelně, pokud interakce jsou malé, invariantem je totální průměr přes úplnou periodu (velkého cyklu),
nebo ? nejméně se relativně mění velká poloosa (nežli energie, moment hybnosti, a nejvíce excentricita, nelžu-li).
Jak plyne z dob oběhů Země, ?Jupiteru, Saturnu.... extrémně? dlouhá perioda Milankovičových cyklů?
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-23 20:31:08
Zelená křivka excentricity
https://upload.wikimedia.org/wikipedia/commons/thumb/5/53/MilankovitchCyclesOrbitandCores.png/800px-MilankovitchCyclesOrbitandCores.png
má během -800 mil let přes nynějšek do +800 mil. let celkem 16 lokálních minim, tedy zhruba po 100 000 rocích, z toho hluboká minima jsou 4 zhruba po 400 000 rocích.
Co to způsobuje? Jupiter a Země na sebe působí gravitačně podle vzdálenosti, která velmi kolísá v hodnotách a také časově, a to i tehdy, když se berou dráhy střední jako kruhové. A k tomu ještě Saturn. Síla Země - Jupiter :
http://pardalnet.wz.cz/PDF/19-Rok-2012-planety-v-primce.pdf
2,16477E+18 N nejblíže k sobě Jupiter, Země a Slunce v přímce
9,54292E+17 N nejdále od sebe (Jupiter za Sluncem vzhledem k Zemi)
A k tomu ještě to, že skutečně nejmenší vzdálenost bude, když budou Slunce, Země, Jupiter ( třeba i Saturn)v tomto pořadí v jedné přímce a Země bude v apohéhiu a Jupiter ( třeba i Saturn ) v aféliu. To při době oběhu 1 rok, 5 let a 12 let je slušný zamotanec možností. Milankovič hlavní věci spočítal jako Srb zajatý za 1.svět. války, který se dostal do knihovny v Budapešti. Odvedl matematicky neskutečnou práci. Být zajatcem čísel bylo asi lepší než válčit na frontě.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-24 07:09:52
Jeví se mi, že více jak 2 superkonjukce nedokáže přežít žádný zajatec.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-25 14:57:56
Panu Hrnčiříkovi - co se týče existence invariantu v té poruchové nebeské mechanice, tak tam se to odvíjí od vyjádření celkové energie planety (tedy součtu její kinetické a potenciální energie) pro její povodní neporušenou eliptickou dráhu. Tato celková energie je rovna:
E = -(1/2) k m M / a
kde k je Newtonovská gravitační konstanta, m je hmota planety (zde Země), M je hmota Slunce, a je délka velké poloosy. Tento výsledek platí pro neporušenou elipsu přesně, nikoliv jen přibližně. Vidíme tedy, že je závislý na délce velké poloosy, ale nikoliv na excentricitě.
Proto zde během drobných poruch od okolních těles existuje prostor, jak variovat dráhu Země aniž by byla změněna celková energie pro oběh Země kolem Slunce, a to změnou excentricity beze změny velké poloosy. Proto když vezmeme už byť jen jedinou další planetu, Jupiter, tak tedy existuje možnost, jak v důsledku poruch variovat excentricity obou těchto planet, aniž by to změnilo celkovou energii pro oběh každé z nich. Jinými slovy, takovéto variace drah obou planet jsou "zadarmo", ve smyslu že k jejich realizaci není zapotřebí měnit celkovou energii ani Země, ani Jupitera.
Dlužno říct, že předpoklad konstantnosti velké poloosy platí dobře pro regulární planety, nikoliv ale už pro planetky, pro které se při perturbacích jejich drah mění i velká poloosa. Což ale souvisí s tím, že energie potřebná na změnu jejich velké poloosy není zase až tak velká, s přihlédnutím k velmi malé hmotnosti těchto planetek. Dalo by se to parafrázovat slovy, že pro regulární planety to není zase až tak bolestné zatáhnout tento energetický účet za ty malé planetky.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-25 19:49:51
Díky.
Jasně a k věci jako vždy.
Vlastně to bylo cítit již z toho "adiabaticky".
Tušil jsem že to tak dopadne, že kvůli energii Mechanik obětuje pouhý? moment hybnosti.
I když mě stále fascinuje podivně dlouhá perioda(y) těchto (složených) cyklů;
nejsa mocen variačního počtu, marně se sebe ptám, zda kvůli nějakému vysokému principu jsou preferovány kruhové dráhy, nebo je to jen pošetilé přání starých Řeků mít dokonalost v jednoduchosti; či pouhý důsledek průměrování a brutálního zaokrouhlování?
Pohyby v centrálním gravitačním poli jsou pěkně popsány v "Fyzikální olympiáda; družice... .
Použitím místní parametrické rovnice elipsy v ohniskovém tvaru jsem se při konst. a prointegroval k průměrné solarizaci za jednotku doby úměrné 1/b**3 ; tj. úměrné(1-e*e)**-3/2
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-25 21:16:03
No pokud jste to integroval jako 1/r^2 přes čas, tak tam s parametrickým vyjádřením elipsy nevystačíte, protože samotná rovnice elipsy neobsahuje tu dynamiku, tj. nijak z ní neplyne, jak rychle se ta planeta po té elipse pohybuje. Její rychlost se zvyšuje v periheliu a klesá v afeliu, takže v periheliu se více ohřeje, ale stráví tam méně času než v afeliu, a to integrace 1/r^2 přes úhel místo přes čas nezohledňuje, musí se to proto integrovat přes čas. To by mohl být důvod, proč Vám vyšlo (1-e^2)^(-3/2) místo (1-e^2)^(-1/2). Jenom tipuju, nevím jak jste postupoval.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-26 09:13:13
Díky.
Už jsem chtěl přes numerické řešení K. rovnice přes anomálie počítat r(t) a numericky počítat časové průměry 1/ri**2 . Abych to nemusel dělat a trápit se s výsledky, zkusil jsem vyjádřil dti=ri*dfíi/(2W)
Násilím jsem zahnal pochybnosti o správnosti tohoto vztahu (tj. diferenciálu plochy).
W = pro daný oběh konstantní a úměrno b,
parametr p v opsaném vzorečku rovnice elipsy = poloměr oskulační kružnice v hlavním vrcholu = úměrný b*b.
Před integrálem přežilo 1/b**3, v integrálu mě vyděsilo e*cos(fí) v součtovém členu, ale uklidnil mě pohled na cosinusoidu.
No a pak jsem opsal a*a=b*b+e*e a vyšlo mi co mi vyšlo, protože dT/db = 0.
Až sem mi to připadalo středoškolské.
Kde jsem ve FO udělal chybu a byl vyřazen?
Jak odvodit b(t) pochopitelně vůbec netuším, ale o to snad vlastně ani nešlo.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-26 16:23:10
Takhle, možná by mi pomohlo, kdybych věděl, z jakého zdroje přesně čerpáte, protože bychom se snadněji shodli na označení. Nicméně není to podstatné, ten výpočet uvedu zde, protože opravdu není složitý. Využijeme pro něj s výhodou faktu, že moment hybnosti a celková energie se zachovávají. Pro moment hybnosti to sice platí na rozdíl od celkové energie pouze při konstantní excentricitě e, ale to v našem výpočtu vadit nebude, protože naším úkolem je spočíst poměr mezi dvěma celoročními slunečními příkony, jedním počítaným pro nějaké nenulové e, a jedním referenčním, za který vybereme příkon na kruhové dráze, tedy s nulovým e. Změny e v čase, stejně tak tedy i změny b v čase, nás tedy nezajímají.
Počítáme tedy integrál:
I(e)=integral_0->T 1/r(t)^2 dt
tedy přes čas v mezích od 0 do T, kde T je doba oběhu, r(t) je vzdálenost od Slunce v čase t. Integraci přes čas t si převedeme na integraci přes úhel fi pomocí úpravy diferenciálu:
dt=(dt/dfi)dfi=dfi/(dfi/dt)
Ve jmenovateli máme dfi/dt, což je úhlová rychlost, označme ji omega(t), kde jsme označením zdůraznili, že úhlová rychlost závisí na čase t. Máme tedy:
dt=dfi/omega(t)
čímžto náš integrál přes oběžnou dobu přejde na integrál přes úhel od 0 do 2pi:
I(e)=integral_0->2pi [1/(r(t)^2 omega(t)] dfi
Abychom mohli tuto integraci provést, museli bychom umět vyjádřit čas t jako funkci úhlu fi a dosadit, pak by integrand byl požadovanou funkcí fi, když integrujeme přes fi. My si tuto práci ovšem můžeme ušetřit, protože výraz r(t)^2 omega(t) je ve skutečnosti pro pevné e konstanta. To zjistíme ze vztahu pro moment hybnosti L(e) vyjádřený v polárních souřadnicích:
L(e) = m r(t)^2 omega(t)
kde m je hmotnost Země. Dosazením do našeho integrálu tedy máme:
I(e)= integral_0->2pi m/L(e) dfi = m/L(e) integral_0->2pi dfi = 2pi m/L(e)
kde jsme využili toho, že m ani L(e) nezávisí na čase t (tedy ani na úhlu fi).
Zbývá tedy spočíst L(e). K tomu zapojíme další zachovávající se veličinu, a to celkovou energii. Tu vyjádříme jako:
E(e)= (1/2)m v(t)^2 - k m M /r(t)
kde v(t) je rychlost Země, k Newtonova gravitační konstanta a M je hmotnost Slunce. V označení E(e) jsme vyznačili potenciální závislost celkové energie na excentricitě e - ve výsledku zjistíme, že ve skutečnosti E na e nezávisí, ale teď to jako ještě nevíme.
Kvadrát rychlosti v(t)^2 má v polárních souřadnicích tvar:
v(t)^2 = (dr/dt)^2 + r(t)^2 (dfi/dt)^2 = (dr/dt)^2 + r(t)^2 omega(t)^2
je tedy součtem kvadrátu radiální rychlosti (dr/dt)^2 a kvadrátu tangenciální rychlosti r(t)^2 omega(t)^2. Výpočet si usnadníme, pokud použijeme dvě polohy, ve kterých je radiální rychlost nulová, těmito polohami jsou perihelium a afelium, ve kterých se nám tedy rychlost redukuje pouze na tangenciální rychlost r(t)omega(t). Nechť d je vzdálenost mezi středem elipsy a ohniskem, a je velká poloosa, b malá poloosa. Pro vzdálenost r_p v periheliu pak dostaneme:
r_p = a-d
pro vzdálenost r_a v afeliu pak:
r_a = a+d
Excentricita e je definována jako:
e = d/a
Z vlastností elipsy plyne vztah d^2 = a^2 - b^2.
Označme úhlovou rychlost v periheliu jako omega_p, v afeliu jako omega_a. Celková energie je konstantní, tedy stejná v periheliu jako v afeliu, odkud tedy máme:
E(e)= (1/2)m r_p^2 omega_p^2 - k m M/r_p
= (1/2)m r_a^2 omega_a^2 - k m M/r_a
kde jsme využili nulovosti radiální rychlosti v periheliu a afeliu. Po dosazení za r_a a r_p máme tedy (označme tento vztah jako [1]):
(1/2)m (a-d)^2 omega_p^2 - k m M/(a-d) = (1/2)m (a+d)^2 omega_a^2 - k m M/(a+d)
Zároveň víme, že moment hybnosti se také zachovává, je tedy stejný v periheliu jako v afeliu, tedy:
L(e) = m r_p^2 omega_p = m r_a^2 omega_a
odkud dostaneme vztah mezi úhlovou rychlostí v afeliu a periheliu:
omega_a = (r_p^2/r_a^2) omega_p = [(a-d)^2/(a+d)^2] omega_p
Z jmenovatele a čitatele vytkneme a^2 a pokrátíme, a využijeme vztahu e=d/a, tj. máme:
omega_a = [(1-e)^2/(1+e)^2] omega_p
Dosazením do vztahu [1] máme:
(1/2)m (a-d)^2 omega_p^2 - k m M/(a-d) = (1/2)m (a+d)^2 [(1-e)^4/(1+e)^4] omega_p^2 - k m M/(a+d)
Vynásobíme 2, vydělíme m, dosadíme identity (a-d)=a(1-e), (a+d)=a(1+e), vydělíme a^2 a převedeme kinetické členy na jednu a potenciální členy na druhou stranu rovnice, čímž máme:
{(1-e)^2 - [(1-e)^4/(1+e)^2]} omega_p^2 = 2k M/a^3 [1/(1-e)-1/(1+e)]
Složená závorka vlevo vyjde po drobné úpravě jako 4e (1-e)^2 /(1+e)^2, hranatá závorka vpravo jako 2e/(1-e)(1+e), tedy po vydělení 4e a vynásobení (1+e)^2/(1-e)^2 máme:
omega_p^2 = (k M/a^3) (1+e)/(1-e)^3
Nyní už tedy můžeme vyjádřit L(e) jako funkci e:
L(e) = m r_p^2 omega_p = m a^2(1-e)^2 odm[k M (1+e)/(1-e)^3]
= m a^2 odm[k M (1-e^2)]
Dosazením do našeho kýženého integrálu tedy máme:
I(e) = 2pi m/L(e) = 2pi / {a^2 odm[k M (1-e^2)]}
Nás zajímá poměr I(e)/I(0), ve kterém se vykrátí konstanty jako a, k a M, tedy:
I(e)/I(0) = 1/odm(1-e^2)
což bylo dokázati (qed).
Mimochodem, dosazením vztahu pro omega_p do vztahu pro celkovou energii pak dostaneme:
E(e)= (1/2)m (a-d)^2 omega_p^2 - k m M/(a-d) =
= (1/2)m a^2 (1-e)^2 (k M/a^3) (1+e)/(1-e)^3 - (k m M /a) 1/(1-e) =
= (1/2) (k m M/a) (1+e)/(1-e) - (k m M /a) 1/(1-e) =
= (1/2) (k m M/a) [1/(1-e)] [(1+e)- 2] =
= -(1/2) k m M/a
Vidíme tedy, že ve celková energie E opravdu nezávisí na excentricitě, pouze na velké poloose a.
Toť vše :-)
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-26 19:53:41
Díky.
Píšete jako kniha, přímo jako knihy, jakož i povolený doping pro fyzikální olympioniky, text příprav pro FO "... .družice".
Však jsem taky psal, že pochyby o napsaném výrazu pro konstantní plošnou rychlost W (alias moment hybnosti) jsem potlačil hrubou silou (spokojen, že budu integrovat podle úhlu). Nenamaloval jsem si ani náčrt, ani neprovedl rozměrovou analýzu ani se pyšně nepodíval do textů (myslel jsem si, že si to přece pamatuji) a tím mi tam potom chyběla mocnina r, a r nezmizelo pokrácením. Kdybych to dosadil správně, tak by mě to vyšlo stejně jako Vám a nemusel bych ani hledat tu parametrickou rovnici elipsy s r a strašidelným cos.
To vše pochopitelně v textu pro FO bylo, ba i mnoho navíc.
Váš postup je však mnohem přímočařejší, zcela obecný, vychází pouze ze 2 dogmat zachování a stačí vyjít z naprosto jednoduché vlastnosti elipsy.
Jasné rámce, obecné, přehledné a rychlé. Dokázané.
Momentu hybnosti se mi dařilo vyhýbat bezmála 50 let, chybou se snad poučím.
Pokusím se zapamatovat si symboly i operátory.
Díky za doučování.
Pavel Brož
,2016-11-26 21:10:50
Jenom ještě, že bych v souvislosti s tím chtěl upozornit na tzv. "100,000-year problem", viz https://en.wikipedia.org/wiki/100,000-year_problem . Jedná se o to, že numericky ty variace příkonu v důsledku změn excentricity dávají řádově nižší hodnoty, než jaké korespondují ke geologickým teplotním záznamům. Pokud totiž vyjdeme ze současné excentricity 0,0167, tak i kdyby nám v průběhu dalších 30 000 let nakrásně vymizela úplně, dostali bychom pokles příkonu relativně pouze o 0,00014, tj. o cca 0,19 W/m^2. Ze zvědavosti jsem si prohlížel článek http://gnosis9.net/pdf/globalni-otepleni-1-dil.pdf, na nějž tady dal odkaz pan Florian, a úplně mě šokoval graf 33, kde se předpovídá pokles relativního příkonu až o 9W/m^2 - což je pochopitelně naprostý blábol. Těch 9W/m^2 může tak maximálně odpovídat jakési ekvivalentní hodnotě poklesu příkonu pro předpovídanou hodnotu oteplení, nikoliv ale přímo poklesu příkonu v důsledku poklesu excentricity. Jistě, pan Florian tady zmínil jakési kumulativní vlivy atd. atd., prima, ale kumulativní vlivy se týkají teploty, nikoliv poklesu hodnoty příkonu v důsledku změny excentricity. To není nic proti panu Florianovi, on pouze odkázal na dokument, ve kterém je shrnutí ještě z jiných dokumentů, takže to není výtka vůči němu osobně.
Ten 100000 year problém je v kostce právě o tom, že numerické variace příkonu v důsledku variací excentricity řádově zaostávají za tím, co je vidět v geologických teplotních záznamech. Zkrátka a dobře řečeno, Milankovičovy cykly nabízejí kolísání vícero veličin majících vliv na sluneční příkon. Těmito veličinami jsou změna náklonu zemské osy, dále precese zemské osy, dále změny excentricity, dále změny náklonu oběžné dráhy Země (tuto změnu ve skutečnosti Milankovič neuvažoval, ale dnes se s ní počítá), a stáčení dráhy perihelia. Každá tato veličina kolísá s nějakou periodou (event. se dají připsat jedné veličině i periody dvě, které vykreslí složitější průběh). Tyto vypočtené periody se porovnají s geologickým teplotním záznamem. A hle - v geologickém záznamu je za poslední milion let nepřehlédnutelná 100000 letá kvaziperioda. Jukněmež tedy do Milankovičovy teorie, jestli v ní nenajdeme něco s touto periodou - a vida, najdeme, excentricita variuje zhruba s touto periodou. Hosana, zvítězili jsme, můžeme klimajuchat!
Bohužel ale jucháme předčasně. Ty variace excentricity nemohou vést k tak velikým výkyvům teplot, leda bychom naši teorii dofutrovali nějakýma dodatečnýma hypotézama. V článku https://en.wikipedia.org/wiki/100,000-year_problem je takových hypotéz zmíněno šest:
- hypotéza klimatické rezonance: předpokládáme, že klima má jakousi "přirozenou vlastní frekvenci" zhruba 100000 let, a zmíněná kvaziperiodicita excentricity se zrovna do této rezonance trefuje. Výsledkem je pak samozřejmě očekávatelné zmnohonásobení odezvy;
- náklon oběžné dráhy Země (tedy to, co Milankovič neuvažoval): tato veličina variuje s frekvencí 100000 let, zatímco excentricita má striktně vzato dvě kvaziperiody, jednu 95000 let a druhou 125000 let. Samotná změna náklonu orbity by ale nevedla k variaci slunečního příkonu, proto jedna z dalších dodatečných hypotéz je, že během tohoto náklonu by se Země mohla prodírat hustými prachovými oblaky, které by snižovaly dopadající sluneční příkon;
- precesní cykly: precese má cyklus zhruba 21636 let, předpoklad je, že např. pouze každý čtvrtý nebo pátý precesní cyklus může vést např. k výraznější změně zalednění. Tato myšlenka není až tak úplně pitomá, protože teorie deterministického chaosu podobné odezvy v násobcích základních period u mnoha nelineárních systémů předpovídá;
- fluktuace slunečního vyzařování: nicméně tam se opět musí předpokládat další hypotéza, která by to vysvětlovala;
- tzv. Doleův efekt - viz https://en.wikipedia.org/wiki/Dole_effect . Jedná se o to, že geologické teplotní záznamy jsou zhusta postavené na měření relativní koncetrace izotopu kyslíku O18. Doleův efekt ukazuje, že na tuto koncentraci má vliv i pozemská a oceánská fotosyntéza. Jinými slovy, toto vysvětlení spíše relativizuje spolehlivost geologických teplotních záznamů měřených podle O18, spíše než aby vysvětlovalo stotisícletou periodu v teplotě, natož pak pomocí variací excentricity;
- hypotéza variace "pracho-ledového" albeda: podle této hypotézy poslouží příkonový pokles způsobený Milankovičovými cykly pouze jako iniciátor zalednění, které ale v důsledku zvýšení odrazivosti zemského povrchu má tendenci být trvalé, tj. nevyrovná se následnými Milankovičovými maximy. Po nějaké době dojde v důsledku poklesu CO2 k podusení vegetace a ke vzniku velkých pouští, jako v Číně a Mongolsku. Tyto pouště následně generují prach, který zvýší albedo a Země opět roztaje.
Dlužno říct, že každá z těchto ad hoc hypotéz je spíše jenom taková z nouze ctnost, a žádná z nich - snad s výjimkou hypotézy o vlivu náklonu orbity - samozřejmě neumí vysvětlit ten stotisícletý cyklus. Tak např. hned ta první hypotéza o klimatické rezonanci vlastně tvrdí, že klima má vlastní frekvenci 100000 let, nenabízí ale žádné vysvětlení, proč by tuto frekvenci mělo mít (pokud se tedy nechceme točit v argumentačním kruhu a tvrdit, že tuto frekvenci přece má proto, že pak lícuje s Milankovičovou variací excentricity a s geologickými teplotními záznamy).
Takže takhle. Zdůrazňuji, že nejsem žádný zavilý klimaskeptik, nicméně docela velký prostor pro to nechávat si skeptický odstup od dílčích klimatologických tezí zde bezesporu je.
A mimochodem, jenom takovou perličku - při čtení onoho dokumentu jsem na stránce 23 dole narazil na takový roztomilý nesmysl: "Vzdálenost Země od Slunce je ovlivněna tím, že Země obíhá kolem těžiště (barycentra) sluneční soustavy, ..." Prosím vás, pokud toto čtete nějací studenti fyziky ještě před zkouškou z klasické mechaniky, nechte si poradit, a neudělejte tu chybu, že se s tímto tvrzením vytasíte u zkoušky. Zkoušející by vám vrátil index s nedostatečnou a mohli byste začít rozjímat nad bludy rozšířenými v nebeské mechanice. Země opravdu neobíhá kolem těžiště sluneční soustavy, pokud se o tom chcete přesvědčit, napište si např. součet gravitačních sil, jakými na Zemi působí Jupiter a Slunce, pro obecnou polohu Země, Slunce a Jupitera. Vycházejte samozřejmě ze známých faktů, jako že vzdálenost Jupitera od Slunce je zhruba pětinásobek vzdálenosti Země od Slunce, a že hmotnost Jupitera je asi tisíckrát menší než hmotnost Slunce. Pokud neuděláte chybu, vyjde vám, že výslednice gravitačních sil, jakými na Zemi působí Jupiter a Slunce, míří obecně mnohem blíže ke středu Slunce než k tomu těžišti (rozdíl samozřejmě vynikne nejlépe když spojnice Země-Slunce a Jupiter-Slunce budou k sobě zhruba kolmé, pokud jsou všechny tři planety v přímce, tak samozřejmě ten směr ke Slunci je stejný jako k těžišti). Nicméně to opět není výtka k panu Florianovi, předpokládám, že ten dokument byl vytvořen na základě prací různých autorů.
Re: Pavel Brož
Stanislav Florian,2016-11-27 10:55:38
Omlouvám se p. Brožovi, že jsem v předchozím příspěvku nereagoval na jeho příspěvek 2016-11-26 21:10:50, který jsem našel až později.
ALE.
https://en.wikipedia.org/wiki/Barycenter
Pro Jupiter :Slunce obíhá kolem barycentra Slunce-Jupiter těsně nad slunečním povrchem.
http://www.cbks.cz/upice2007/9.pdf
Výpočty Hvězdárna Úpice.
Můj názor.
Barycentrum sluneční soustavy během 2000 let se posunulo asi o 0,001 AU. Slunce obíhá kolem barycentra sluneční soustavy. Nevidím důvod proč by Země neměla kolem barycentra sluneční soustavy obíhat rovněž. Nebo jsem nepochopil jaké jsou výhrady proti tomu.
Píšete :"Země opravdu neobíhá kolem těžiště sluneční soustavy".
Nejsem schopen zvládnout matematické výpočty, ale výchozí předpoklady občas jsou divné. Jednou se předpokládá nebo vychází, že velká poloosa je konstantní, jinde vychází, že změny ozáření závisí na změně velké polosy a ne na změně excentricity.
Můj názor : Změny vyvolané excentricitou jsou relativně malé, ale dlouhodobé, což v kombinaci s albedem může stačit jako spouštěcí impulz ke vzniku doby ledové se zpětnou kladnou vazbou.
Kutílek uvádí myslím že až přes 20 W/m2 ?? jako možný rozdíl ozáření někde o obratníku vlivem precese ( nejkrtatší Milankovočův cyklus zhruba 20 000 let). Takže zpochybněný údaj 9W/m2 díky excetricitě snad může znamenat rozdíl mezi nejbližší a nejvzdálenější plohou Země vlivem excentricity. Není to tedy integrovaná změna ozáření podél celé dráhy, která má být relativně malá.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-27 01:11:44
Pro p. Brože, píšete 26.11:
"K tomu zapojíme další zachovávající se veličinu, a to celkovou energii...
Zároveň víme, že moment hybnosti se také zachovává, je tedy stejný v periheliu jako v afeliu....
Vidíme tedy, že ve celková energie E opravdu nezávisí na excentricitě, pouze na velké poloose a."
Já to nevidím. Změny excentricity dráhy Země jsou dány tím, že Země neobíhá kolem Slunce, ale kolem barycentra sluneční soustavy, barycentrum ovlivňuje zvláště Jupiter a Saturn. Na soustavu Země -Slunce tedy působí VNĚJŠÍ způsobená hlavně Jupiterem a Saturnem. Zákony zachování energie a momentu hybnosti platí v uzavřené soustavě, neplatí tedy na soustavu Slunce a Země, ale na soustavu Země a barycentrum ( Slunce + ostatní planety a sna i Měsíc).
Jednoduše řečeno, Jupiter působí na Zemi silou, která je příčinou deformace elipsy oběhu Země, do soustavy Země-Slunce energii vzhledem k Zemi dodává i odebírá podle vzdálenosti a hodnoty kolísají vzhledem k době oběhu 1 rok Země a 12 let Jupiteru.
https://upload.wikimedia.org/wikipedia/commons/thumb/5/53/MilankovitchCyclesOrbitandCores.png/800px-MilankovitchCyclesOrbitandCores.png
Komentář: graf sestavili astronomové a jasně vyjadřuje, že teploty ( zelená křivka dole ) souvisí s excentricitou ( zelená křivka nahoře.. Také Kutílek v knize Globální oteplování racionálně píše, že menší excentricita => ochlazení.
Graf 28 na
http://pardalnet.wz.cz/PDF/37-Globalni-oteplovani-1.dil.pdf
dobře ukazuje, že maxima excentricity odpovídají vyšší teplotě a nízká excentricita dobám ledovým.
Dále graf 21 ukazuje vynikající shodu globálních teplot podle vrtu Vostok a koncentrace ppm CO2. Ukázat na něm předstih zvyšování teploty před ppm CO2 je v tomto měřítku těžké, jedná se o desítky až stovky let, kdy následně po zvýšení teploty roste ppm CO2 uvolněný z oceánů ( klimatolog Bourton).
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-27 17:10:49
Pane Floriane, s tím těžištěm opravdu nemáte pravdu. Nijak Vám to nezazlívám, jde totiž o opravdu zažitý mýtus, který podle všeho vznikl z toho, že to tvrzení, že těleso obíhá kolem těžiště, je platné - a to absolutně přesně - v soustavě právě dvou těles. Z toho pak někteří lidé usuzují, že musí platit obecně, i pro soustavu tří a více těles, kde to ale už není pravda. Uvedu ilustrativní příklad, z něhož bude naprosto zřejmé, že tvrzení o oběhu kolem těžiště v soustavě tří těles je naprosto zcestné. Mějme dvě velmi hmotná tělesa o poměru hmotností dejme tomu 1:10. Tato dvě tělesa budou obíhat kolem společného těžiště, přičemž vzdálenost toho hmotnějšího od těžiště bude desetinová vzhledem ke vzdálenosti toho mého hmotnějšího od těžiště. Pro konkrétnost, zvolme nějaké jednotky, ve kterých bude vzdálenost toho hmotnějšího tělesa od těžiště 1, tedy potom vzdálenost toho méně hmotnějšího od těžiště bude deset.
Nyní do tohoto systému přidejme třetí naopak málo hmotné těleso, položme ho do blízkosti těžiště těch dvou hmotných - dejme tomu do vzdálenosti 0,001 od těžiště - a udělme mu jen malou tangenciální rychlost vzhledem k tomu těžišti. Toto těleso svou přítomností sice změní celkové těžiště soustavy, ale extrémně málo, a to hned ze dvou důvodů - jednak jsme ho vybrali jako lehké vzhledem k těm dvěma těžkým, a jednak jsme ho položili velmi blízko těžiště těch dvou předchozích těles - platí totiž, že když do těžiště dvou těles položíte libovolně těžké třetí těleso, poloha výsledného těžiště nyní už tří těles bude stejná jako poloha těžiště původních dvou těles.
Pokud by platilo, že třetí těleso má obíhat kolem společného těžiště soustavy, pak by mělo obíhat kolem tohoto těžiště, jelikož jsme mu udělili jen malou tangenciální rychlost vzhledem k těžišti, a je od něj jen maličko vzdáleno (tisíckrát méně než nejhmotnější těleso soustavy a desettisíckrát méně než to méně hmotné z těch dvou těžkých těles). To třetí těleso by kolem toho těžiště mohlo obíhat, kdyby výsledná síla působící na něj aspoň zhruba mířila směrem k těžišti. Pojďme si tuto výslednou sílu nyní spočítat. Nejhmotnější těleso soustavy je vzdáleno od našeho třetího tělesa ve vzdálenosti 1 plus minus 0,001, v závislosti kde přesně kolem těžiště se třetí těleso nachází. Druhé nejhmotnější těleso je od našeho třetího vzdáleno 10 plus minus 0,001. Spočteme poměr sil, jakými dvě hmotná tělesa působí na naše třetí těleso - dosazením do Newtonovy gravitační síly k m M/r^2 zjistíme, že nejhmotnější těleso působí na naše třetí těleso tisíckrát větší silou, než jakou na ně působí druhé nejhmotnější těleso, protože prostě v čitateli máme desetkrát větší hmotu, zatímco ve jmenovateli máme kvadrát desetkrát menší vzdálenosti - výsledný poměr sil je tedy 1000:1 ve prospěch nejhmotnějšího tělesa. Z toho vidíme, že naše třetí těleso ani náhodou nebude obíhat kolem společného těžiště, ale (vzhledem ke své malé počáteční rychlosti) zahájí pád směrem k nejhmotnějšímu tělesu. Navíc, jak se k němu bude přibližovat, síla, jakou na něj působí druhé nejhmotnější těleso, se bude zmenšovat (protože vzdálenost k němu poroste), zatímco síla, jakou na něj působí nejhmotnější těleso, se bude naopak zvětšovat.
Povězme si dále, jaký bude další vývoj této tříčlenné soustavy. Třetí těleso - bude-li průměr nejhmotnějšího tělesa dostatečně malý, tj. pokud nedojde ke srážce - proletí po elipse kolem nejhmotnějšího tělesa, projde periheliem, a pak se bude vracet do afelia, které bude blízko jeho výchozí polohy, tedy blízko těžišti (afelium bude těžišti tím blíže, čím menší počáteční rychlost jsme zvolili). Zároveň bude pro dostatečně malou výchozí rychlost velmi malá vzdálenost perihelia třetího tělesa od nejhmotnějšího tělesa. Pro dostatečně malé perihelium tedy můžeme určit velikost velké poloosy této elipsy, která se bude blížit polovině vzdálenosti těžiště od nejhmotnějšího tělesa - tedy v našich jednotkách 0,5. Podle třetího Keplerova zákona je druhá mocnina oběžné doby úměrná třetí mocnině velkých poloos. Pokud předpokládáme, že původní dvě hmotná tělesa obíhají po kruhových drahách (připomínám, že obíhají kolem svého těžiště, protože jak bylo řečeno, tato vlastnost pro soustavu pouze dvou těles opravdu platí), tak vidíme, že poloosa pro druhé nejhmotnější těleso je zhruba dvacetkrát větší než poloosa pro třetí těleso. Odtud nám ze třetího Keplerova zákona vyjde, že oběžná doba třetího tělesa je cca 90 krát kratší než oběžná doba druhého nejhmotnějšího tělesa naší tříčlenné soustavy.
A nyní si udělejme resumé pohybů těchto těles. První dvě tělesa, každé z nich výrazně těžší než třetí těleso, obíhají kolem jejich společného těžiště. Před přidáním třetího tělesa to platí absolutně přesně, po přidání lehkého třetího tělesa už ne úplně přesně, protože přidáním třetího tělesa polohu těžiště maličko ovlivníme - vzhledem k tomu, že jsme ale přidávali lehké těleso, plus navíc do blízkosti původního těžiště, půjde o změnu naprosto zanedbatelnou. Třetí těleso svou malou hmotou pohyb těch dvou těžkých prakticky neovlivní, proto bude i nadále platit, že tato dvě tělesa obíhají kolem společného těžiště (v našem zadání je celkem jedno, jestli toto těžiště bereme jako těžiště pouze dvou původních těles anebo jako těžiště všech tří těles, protože obě tato těžiště budou mít téměř stejnou polohu). Takže vidíme, že na oběhu dvou nejhmotnějších těles se prakticky nic nemění, obíhají nadále kolem společného těžiště. Platí to ale i pro třetí těleso? Ani náhodou!!! Třetí těleso obíhá kolem elipsy, v jejímž ohnisku je nejtěžší těleso soustavy. Druhé nejtěžší těleso soustavy na naše třetí těleso působí maximálně tisíckrát menší silou, než to nejhmotnější těleso, jeho působení bude proto znamenat pouze velice malou poruchu k eliptickému pohybu třetího tělesa kolem toho nejhmotnějšího. To je přesně ten důvod, proč ta výsledná síla, jakou Jupiter a Slunce působí na Zemi, míří mnohem přesněji ke středu Slunce, než ke společnému těžišti.
Zároveň platí, že díky mnohem kratší oběžné době třetího tělesa vzhledem k oběžné době druhého tělesa, se oběžná dráha třetího tělesa kolem toho nejhmotnějšího stíhá adaptovat na změnu polohy nejhmotnějšího tělesa. Připomeňme, že i to nejhmotnější těleso obíhá; obíhá kolem těžiště jaké má s tím druhým tělesem, tedy jeho poloha se mění, ovšem s periodou cca 90 krát větší než je doba oběhu toho třetího tělesa. Proto se během svých oběhů to třetí těleso stíhá celkem dobře adaptovat, a jeho trajektorie vzhledem k nejhmotnějšímu tělesu bude s velikou přesností elipsa.
Zkusme si nyní podmínky z tohoto příklady zadaptovat na systém Slunce-Jupiter-Země. Nejmenší vzdálenost Země k Jupiteru je zhruba 4 AU (naopak největší vzdálenost skoro až 6,5 AU, když je Jupiter v aféliu), vzdálenost Země-Slunce je definitoricky 1 AU. Hmotnost Jupitera je cca tisíckrát menší než hmotnost Slunce. Odtud z Newtonovy gravitační síly dostaneme, že Slunce působí na Zemi silou více než 16 tisíckrát větší než Jupiter (v předchozím příkladu nám tento poměr vyšel 1000). Podobným způsobem jako v předešlém příkladu i nyní bychom snadno došli k závěru, že pro pohyb Země je naprosto dominantní přitažlivost Slunce, zatímco Jupiter působí jen velice malé perturbace na dráhu Země kolem Slunce. Tato dráha je s velikou přesností eliptická v soustavě spjaté se Sluncem (tedy v soustavě, v níž se Slunce nepohybuje). Jupiter se Sluncem se vzájemně pohybují kolem jejich společného těžiště, ale nikoliv už Země, ta se v soustavě spojené se Sluncem pohybuje po elipse, v jejímž ohnisku je střed Slunce, nikoliv těžiště. V soustavě spojené s těžištěm (tedy v soustavě, v níž se těžiště nepohybuje, a v níž se naopak pohybuje Slunce) už je pohyb Země složitější, protože Slunce se v této soustavě pohybuje s periodou 11,86 let, takže elipsa, po níž se pohybuje Země, se pohybuje spolu se Sluncem. Nicméně ani v této soustavě neplatí, že by Země obíhala kolem těžiště, bez ohledu na to, jestli jde o těžiště pouze Jupitera a Slunce, anebo o těžiště všech tří těles (Země svou relativně malou hmotou - cca 318 krát lehčí než Jupiter a cca 330 tisíckrát lehčí než Slunce) toto těžiště prakticky neovlivní.
Nyní už doufám, že je jasné, jak to je, a že už nezbyl žádný prostor pro další obhajobu naprosto neobhajitelného tvrzení, že Země obíhá kolem těžiště sluneční soustavy.
Co se týče výpočtu polohy toho těžiště, tak na to se nemusíme odvolávat na hvězdárnu v Úpici, to přece zvládne každý středoškolák - poměr hmotností Jupitare a Slunce je 1:1000, tedy poměr vzdálenosti Jupitera k těžišti ke vzdálenosti Slunce k těžišti je tím pádem taky 1:1000, tedy těžiště je ve vzdálenosti cca 0,005 AU od středu Slunce, což dá těch cca 750 tisíc km. S přihlédnutím k přesnějšímu poměru hmot Jupiter-Slunce, který je 1:1047. dostaneme přesnější hodnotu 716 tisíc km. Což je zhruba poloměr Slunce, proto to těžiště leží zhruba na povrchu Slunce, může být i pod ním (pokud zohledníme vliv dalších planet, který je ale malý). Je nicméně nutné říct, že poloha toho těžiště vůči středu Slunce variuje, jelikož variuje i vzdálenost Jupiter-Slunce. Pro Jupitera v aféliu vyjde 782 tisíc km, což už bude určitě nad povrchem Slunce.
Co se týče té variace toho příkonu, ano, napadlo mě to, že těch 9 W/m^2 bylo možná myšleno jako rozdíl v příkonu v přísluní, to by tak nějak mohlo být. Celoroční energetický příkon se ale v průměru změní jenom o maximálně těch 0,19W/m^2.
Jinak co se týče Vaší argumentace těmi grafy, tak to je přesně to, co jsem zmiňoval - argumentuje se tím, že dvě veličiny - excentricita a geologické teplotní záznamy - vykazují stejnou periodu. Přitom se ale ignoruje fakt, že vliv té excentricity řádově nesedí na velikost té odezvy, což je ostatně ten dlouho známý 100000 year problém. Aby se se tyto dvě variace na sebe napasovaly, musí se použít dodatečné hypotézy, které zmultiplikují ten vliv variující excentricity. Proto se pak mluví o těch kumulativních a zpětnovazebních vlivech, o jejichž kvantitativním vlivu může současné klimatologie pouze spekulovat.
Zmínil jste dříve, že jeden klimatolog počítá vliv té variující excentricity s předpokladem konstantnosti velké poloosy, zatímco druhý klimatolog s předpokladem měnící se poloosy. Nevím, jestli tomu je tak skutečně, jestli jste tak pouze neusoudil z toho grafu v tom pdfku, na které odkazujete. Jenom mi to asociovalo takový starý vtip, jak se baví dva Rusové v jedoucím vlaku, a ten jeden říká že jede z Petrohradu do Moskvy a ten druhý mu odpoví, že on jede z Moskvy do Petrohradu. Chvíli po rusku mlčky dumají, a pak zvolají: "Vót těchnika!". Píšete, že přitom oba dva klimatologové jsou slovutní odborníci ve svém oboru. Nu - vót klimatológia. S konstantní anebo měnící se velkou poloosou, však ono nakonec něco vyjde, co bude možné vynést do těch grafů :-) Toto prosím berte jenom jako odlehčení tohoto tématu, neznamená to, že považuji klimatology za blbce.
Opět zdůrazňuji, nejsem zavilý klimaskeptik. Nemůžu ani říct, že stojím někde mezi klimaskeptiky a klimaalarmisty, spíše někde úplně mimo jejich spojnice. V žádném případě nezpochybňuji, že by snad klimatologie nebyla věda - je to věda. Vidím mnoho paralel k jiné vědě, kterou také nezpochybňuji - ke kosmologii. Obě dvě vědy umí vytvořit modely, které perfektně sedí na minulost. Obě dvě vědy mají docela mizernou prediktivní sílu pro předpovědi, co se stane v budoucnosti, zvláště pak v té vzdálené. Stačí nový objev, a modely obou věd se pružně refitují, aby adaptovaly dříve neznámá data a aby opět, s novými fity, věrně popisovaly minulost. V kosmologii to byl např. objev zrychleného rozpínání vesmíru, hrála zde ale roli také mnohá upřesnění kosmologických vzdáleností díky mnohem pokročilejším a přesnějším observačním metodám. V klimatologii se vynoří nová data např. co se týče absorbance uhlíku biomasou, no a taky se to flexibilně zrefituje.
Podtrhávám, že toto je můj subjektivní názor, nikomu ho nenutím, ani netvrdím, že nevyhnutelně musím mít pravdu. Pouze tvrdím, že dílčí klimatologické teze opravdu nechávají dostatečný prostor pro to nechat si od nich skeptický odstup.
P.S.: tu otřesnou větu o tom obíhání Země kolem těžiště prosím z toho pdfka odstraňte, nebo k tomu prosím aspoň přidejte nějaké erratum. Děkuji.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-27 18:38:10
Pro Pavel Brož,2016-11-27 17:10:49
Nesouhlasím, když Slunce obíhá kolem barycentra sluneční soustavy ( s Jupiterem i se Saturnem to vyjde těsně pod povrchem Slunce). Tedy Jupiter i Saturn obíhají kolem tohoto barycentra, tak nevím proč by kolem tohoto barycentra neměla obíhat Země.
Počítání jsem pročetl, ale je to pořád dokola KDYBY..TAK BY. Prostě uměle vytvořené zjednodušení za jiných podmínek, od kterých se pak laxně odstoupí ( tu zákon zachování energie a momentu hybnosti pro dvě tělesa, když máme nejméně tři; tu zachování velké poloosy nebo nezávislost na excetricitě, když to právě na nich závisí).
https://cs.wikipedia.org/wiki/Klimatick%C3%A1_zm%C4%9Bna#/media/File:Five_Myr_Climate_Change.svg
Chápu, že není znám důvod, proč nejdříve byla silná závislost teploty od kambria na periodě 40 000 let a nyní na 100 000 let. Hodně asi působí i to, že když je hodně chladno, tak se jinak váže CO2 v chladné vodě atd. Postě jsou jen dva stabilní stavy díky zpětným vazbám- hodně teplo nebo hodně zima, přechody jsou rychlé.
Galaxie se zvolna otáčejí kolem centra galaxie, Slunce oběhlo asi 20 x, nejspíš tam je supermasivní černá díra. Nesrovnalosti této rotace pozorované astronomy vedly k pojmu temná hmota. Temná hmota má být jako pavučiny rozeseta vesmírem. Čili relativně rychlá změna gravitačních poměrů ve sluneční soustavě není nemožná.
Vrt Vostok má vyvozeny teploty z izotopu delta 18O, závislost poměru izotopů kyslíku na zalednění/nezalednění závisí na teplotě jednoduše. Hmotnější izotop se hůře odpařuje, led se pak tvoří primárně z par se zvýšeným obsahem těkavější H2O s kyslíkem 16. Bentonitové usazeniny a poměr isotopů kyslíku ukazují totéž, je to i na grafu Milankovičových cyklů Wikipedie
https://upload.wikimedia.org/wikipedia/commons/thumb/5/53/MilankovitchCyclesOrbitandCores.png/800px-MilankovitchCyclesOrbitandCores.png
Takže nějak nerozumím zpochybňování odchylek 18O izotopu díky fotosyntéze řas a z nich snad (?) sedimentů ( bentonitů ?) v moři.
Moře ostatně bylo geologicky skoro všude. Oceánské dno se rozšiřuje a žádné současné oceánské dno není starší jak 200 milionů let.
Článek je o zpochybňování pozemských globálních teplot rozšiřováním výpočtu do neměřených oblastí. Samozřejmě jsou oblasti, kde se krátkodobě ( několik let) třeba ochlazuje. Ale otepluje se dlouhodobě i na stanicích mimo tepelné ostrovy ( řeknu Horská Kvilda nebo Lomnický štít). A to nemluvím o starých stanicích ( Klementinum). A otepluje se i podle měření automatických mořských stanic ARGO.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-28 00:26:52
Pane Floriane, ten příklad byl zkoncipovaný právě tak, aby vyvrátil tvrzení, že tělesa v soustavě obíhají kolem těžiště. Ty hodnoty jsem zvolil právě tak, aby se ty výpočty mohly udělat snadno z hlavy. Konfiguraci v tom příkladu (např. umístění třetího tělesa blízko těžiště původních dvou) jsem zvolil záměrně, aby bylo naprosto jasné, že to třetí těleso neobíhá kolem společného těžiště, ale s velkou přesností po elipse s největším tělesem v ohnisku. Díky jednoduchosti konfigurace toho příkladu je pak bez nejmenší pochyby jasné, že v systému tří těles obecně neplatí, že tělesa obíhají kolem těžiště.
Dobře, Vám se ta konfigurace zdá umělá, a máte za to, že sice obecně neplatí, že v systému tří těles tato obíhají kolem těžiště, ale že speciálně v případě hodnot platných konkrétně pro Slunce, Jupiter a Zemi by mohlo platit, že Země obíhá kolem těžiště. Dobře, provedu speciálně pro Vás výpočet pro odpovídající hodnoty. Zapotřebí je pouze znalost Newtonova gravitačního zákona, vektorové skládání sil a jednoduché geometrické operace, vše z tohoto se učí již na středních školách. Spočteme směr výsledné gravitační síly, jakou působí na Zemi Jupiter a Slunce, a porovnáme tento směr s polohou těžiště všech tří těles. Spočteme to pro pozici planet, kdy spojnice Země-Slunce je kolmá ke spojnici Jupiter-Slunce, kdy dobře vynikne rozdíl mezi směrem gravitační síly působící na Zemi a směrem k těžišti (pokud jsou totiž všechny tři planety v přímce, tak samozřejmě oba směry jsou logicky stejné, proto volíme toto postavení, kdy planety jsou v pravoúhlém trojúhelníku se Sluncem v pravém úhlu). Nakonec spočteme vzdálenost dvou bodů na spojnici Slunce-Jupiter od středu Slunce – prvním z těchto bodů bude těžiště, druhý z těchto bodů na této spojnici nám určí směr výsledné gravitační síly působící na Zemi. Tento poslední krok nám totiž umožní udělat si představu, jestli výsledná gravitační síla působící na Zemi míří spíše k těžišti, nebo spíše ke středu Slunce, a tím nám i řekne, nakolik je oprávněná představa, že Země obíhá kolem těžiště, a nakolik je naopak oprávněná představa, že Země obíhá kolem středu Slunce.
Až toto všechno budeme mít, tak v identické konfiguraci spočteme pro změnu výslednou sílu, jakou působí na Jupiter Slunce a Země, a určíme, nakolik přesně směřuje tato síla do těžiště všech tří těles. Toto porovnání nám ukáže, proč Jupiter a Slunce s velikou přesností obíhají kolem společného těžiště, zatímco pro Zemi to neplatí.
Takže máme pravoúhlý trojúhelník JSZ, kde jednotlivé vrcholy označují postupně střed Jupitera, Slunce a Země. Pravý úhel je u vrcholu S, tedy ve středu Slunce. Budeme měřit v AU (pro naše účely postačí brát AU=150 miliónů km), takže délka odvěsny J_S (tj. vzdálenost Jupiter-Slunce) je 5 AU, délka odvěsny S_Z (vzdálenost Slunce-Země) je 1 AU, délka přepony J_Z (vzdálenost Jupiter-Země) nám tedy podle Pythagorovy věty vychází jako J_Z = odm(26)=5,099 AU. Hmotnosti počítejme v hmotnostech Země, pro Jupiter tedy máme M_J=318 M_Z, pro Slunce pak M_S=333000 M_Z. Nejprve se podívejme na těžiště – polohu těžiště T3 tří těles lze spočíst tak, že nejprve spočteme polohu těžiště T2 dvou libovolně vybraných těles, a pak spočítáme soustavy složené z třetího tělesa a fiktivního tělesa, které leží v T2 a má hmotu rovnu součtu dvou prve vybraných těles (elementární snadno dokazatelná vlastnost těžiště tří těles je, že přitom nezáleží na tom, která dvě tělesa vybereme jako první dvě a které jako třetí). Takže jako těžiště T2 zvolme např. těžiště Jupitera a Slunce. Poměr jejich hmot je 1:1047, proto vzdálenost Jupiter_T2 je rovna 1047 krát vzdálenost Slunce_T2. Tedy vzdálenost J_T2 je rovna (1046/1047)*J_S=4,9952 AU, zatímco vzdálenost S_T2 je J_S/1047=0,0048 AU. V kilometrech je tedy vzdálenost T2 od S rovna 716332 km. Podle Pythagorovy věty můžeme spočíst vzdálenost Z_T2, vyjde nám Z_T2=1,000011 AU, tedy prakticky 1 AU. Vzdálenost T3 od T2 spočteme jako těžiště soustavy Země a fiktivního tělesa ležícího v T2 a majícího hmotnost M_J+M_Z. Odtud dostaneme, že T3 leží ve vzdálenosti 1/333318=0,000003 AU od T2, tedy v kilometrech dostaneme, že těžiště všech tří těles leží pouze 450 km od T2. Tangens úhlu S_Z_T2 je roven:
tg S_Z_T2=S_T2/S_Z = 0,0048
tedy úhel S_Z_T2 je 0,27 stupňů. Tedy úhel Z_T2_S je 90-0,27=89,73 stupňů. Z kosinové věty potom dostaneme vzdálenost T3_S jako:
T3_S=odm[(T2_T3)^2 + (T2_S)^2 – 2*T2_T3*T2_S*cos 89,73°]
odkud zjistíme, že vzdálenost T3_S je jen o 2,94*10^-6 násobek menší, než vzdálenost T2_S. Jinými slovy, zatímco vzdálenost T2_S nám vyšla 716332 km, vzdálenost T3_S vyjde jako 716330 km. Nyní už si můžeme udělat představu, kde se těžiště T3 nachází – je ve vzdálenosti pouhých 450 km od těžiště Jupiter-Slunce směrem k Zemi, a jeho vzdálenost ke středu Slunce je o pouhé 2 km menší, než vzdálenost těžiště Jupiter-Slunce od středu Slunce. Z toho vidíme, že při praktických výpočtech můžeme rozdíl mezi T2 a T3 prakticky zanedbat.
Nyní se koukneme na úhly, jaký svírá spojnice J_T2 se spojnicí J_T3 (jedná se zároveň o úhel mezi spojnicí J_S a J_T3). Pro tangens tohoto úhlu dostaneme (ne úplně přesně, ale se zanedbatelnou nepřesností):
tg T2_J_T3=T2_T3/J_T2 = (1/333318)*(1/4,9952) = 6*10^-7
tj. úhel T2_J_T3 je zhruba 0,12 úhlových vteřin. To je tedy rozdíl mezi spojnicí Jupiter-Slunce a spojnicí Jupiteru a těžiště všech tří těles (protože úhel T2_J_T3 je totožný s úhlem S_J_T3).
Pro úhel S_Z_T3 dostaneme, že je prakticky roven (opět, s velice zanedbatelnou nepřesností) úhlu S_Z_T2, který nám vyšel jako 0,27 stupňů.
Zrekapitulujme si naše mezivýsledky:
úhel S_J_T3 mezi spojnicí Jupiter-Slunce a spojnicí Jupiter-T3 je 0,12 úhlových vteřin
úhel S_Z_T3 mezi spojnicí Země-Slunce a spojnicí Země-T3 je 0,27 stupňů (tedy 8100 krát větší než předchozí úhel)
Nyní budeme počítat úhly, kam míří výsledná gravitační síla, jakou působí Jupiter se Sluncem na Zemi, a kam míří výsledná gravitační síla, jakou působí Země se Sluncem na Jupiter.
Začněme s výslednou gravitační silou působící na Zemi. Připomeňme, že Slunce je v našem trojúhelníku ve vrcholu s pravým úhlem. Tangens úhlu mezi spojnicí S_Z a J_Z je:
tg S_Z_J = S_Z/Z_J = 5
tedy úhel S_Z_J je 78,69 stupně. Nechť osa x má směr J_S, a osa y směr Z_S. Potom sílu F_J_Z, kterou působí Jupiter na Zemi, můžeme rozložit na složku F_J_Zx a složku F_J_Zy. Dostaneme pro ně:
F_J_Zx = F_J_Z * sin S_Z_J = F_J_Z *sin 78,69 = 0,98058 F_J_Z
F_J_Zy = F_J_Z * cos S_Z_J = F_J_Z * cos 78,69 = 0,19612 F_J_Z
(můžeme zkontrolovat, že sečteme-li kvadráty těchto dvou složek a odmocníme, dostaneme očekávatelně F_J_Z)
Síla, kterou působí Slunce na Zemi, míří ve směru osy y, dostaneme tedy pro její složky:
F_S_Zx = 0
F_S_Zy = F_S_Z
kde F_S_Z je gravitační síla, jakou působí Slunce na Zemi.
Výsledná síla působící na Zemi tedy bude mít složky:
F_Zx = F_J_Zx = 0,98058 F_J_Z
F_Zy = F_J_Zy + F_S_Zy = 0,19612 F_J_Z + F_S_Z
Nyní už tedy není problém spočíst úhel, kam míří výsledná síla. Tento úhel označme alfa, a budeme ho měřit od spojnice Slunce-Země. Pro jeho tangens dostaneme:
tg alfa = F_Zx/ F_Zy = 0,98058 F_J_Z / (0,19612 F_J_Z + F_S_Z) =
= 0,98058 / [0,19612 + (F_S_Z/F_J_Z)]
K vypočtení tohoto tangentu nám tedy stačí spočíst poměr F_S_Z/F_J_Z a dosadit. Pro tento poměr máme:
F_S_Z/F_J_Z = (k * M_Z * M_S / S_Z^2) / (k * M_Z * M_J / J_Z^2) =
= (M_S/M_J) * (J_Z/S_Z)^2 = 1047 * 5,099^2 = 27221,79
tj. dosazením máme:
tg alfa = 0,000036
tedy úhel alfa je 7,43 úhlové vteřiny. Porovnejme ho s úhlem mezi spojnicí S_Z a Z_T3, který vyšel jako 0,27 stupňů, tedy 131 krát větší. Pokud bychom chtěli najít bod A na spojnici J_S, na nějž ukazuje směr výsledné síly působící na Zemi, tak tento bod se nachází zhruba 5400 km od středu Slunce, zatímco T3 se nachází ve vzdálenosti 716330 km od středu Slunce. Připomínám, že T3 je přitom jen 450 km vzdálen od spojnice J_S.
Pokud budeme tvrdit, že Země obíhá kolem společného těžiště, vznikne nám v tomto postavení planet chyba ekvivalentní 716330-5400 = 710930 km. Pokud místo toho budeme tvrdit, že Země obíhá kolem středu Slunce, uděláme chybu jen 5400 km. Které tvrzení je tedy přesnější? Samozřejmě, že to druhé, a to o dva řády.
Nyní se koukněme, jak dopadneme s rozborem výsledné gravitační síly, kterou působí Slunce se Zemí na Jupiter. Sílu, jakou působí Země na Jupiter už spočtenou máme, její velikost je samozřejmě identická se silou, jakou působí Jupiter na Zemi, liší se jen orientace té síly. Pro její složky tedy máme:
F_J_Zx = F_J_Z * sin S_Z_J = F_J_Z *sin 78,69 = 0,98058 F_J_Z
F_J_Zy = F_J_Z * cos S_Z_J = F_J_Z * cos 78,69 = 0,19612 F_J_Z
Pro složky síly, jako působí Slunce na jupiter, máme:
F_S_Jx = F_S_J
F_S_Jy = 0
Výsledná síla působící na Jupiter má tedy složky:
F_Jx = F_J_Zx + F_S_Jx = 0,98058 F_J_Z + F_S_J
F_Jy = F_J_Zy + F_S_Jy = 0,19612 F_J_Z
Můžeme tudíž spočíst úhel, kam míří výsledná síla. Tento úhel označíme jako beta a budeme ho měřit od spojnice J_S. Pro jeho tangens dostaneme:
tg beta = F_Jy / F_Jx = 0,19612 F_J_Z / (0,98058 F_J_Z + F_S_J)
= 0,19612 / [0,98058 + (F_S_J/F_J_Z)]
Stačí tedy spočíst poměr F_S_J/F_J_Z a dosadit. Pro tento poměr máme:
F_S_J/F_J_Z = (k * M_S * M_J / S_J^2) / (k * M_J * M_Z / J_Z^2) =
= (M_S/M_Z) * (J_Z/S_J)^2 = 333000 * (5,099/5)^2 = 346317,35
kde jsme dosadili 333000 jako poměr mezi hmotou Slunce a Země, 5,099 AU jako vzdálenost Země-Jupiter a 5 AU jako vzdálenost Jupiter-Slunce.
Dosazením tedy máme:
tg beta = 5,66 * 10^-7
čemuž odpovídá úhel 0,11 úhlové vteřiny. Připomeňme, že úhel mezi spojnicí Slunce-Jupiter a Jupiter-T3 nám vyšel 0,12 úhlové vteřiny (oba mají stejnou orientaci, tj. jsou od spojnice J_S měřeny ve stejném směru otáčení). Vidíme, že v případě Jupitera výsledná síla velice přesně míří do výsledného těžiště všech tří těles. Nicméně k enormně nízké hodnotě tohoto úhlu (úhel mezi výslednicí sil a směrem k T3 vyšel v případě Země 67 krát větší – stačí podělit úhel alfa a beta) neuděláme velkou chybu dokonce ani v případě, kdy místo těžiště všech tří těles budeme u pohybu Jupitera používat jenom jeho těžiště se Sluncem, bez uvažování Země.
Takže závěr je:
Představa, že Země obíhá kolem těžiště sluneční soustavy, je naprosto zcestná. Země totiž s mnohem větší přesností obíhá kolem středu Slunce – neplatí to samozřejmě přesně, ale chyba, kterou uděláme, je o dva řády nižší než chyba, kterou vytvoříme při předpokladu, že Země obíhá kolem těžiště sluneční soustavy.
Naopak, představa, že Jupiter obíhá kolem těžiště sluneční soustavy, nevede k takové chybě, protože směr, kterým míří výslednice sil působící na Jupiter se jen zanedbatelně liší od směru ke společnému těžišti. Navíc v tomto případě, vzhledem k velmi malé vzdálenosti těžiště T3 od těžiště T2 počítaného pouze jako těžiště dvoučlenné soustavy Jupiter-Slunce (připomeňme, že tato vzdálenost je pouhých 450 km, ve srovnání se 716330 km, což je vzdálenost T3 od středu Slunce), můžeme klidně „trojčlenné“ těžiště T3 nahradit pouhým těžištěm Jupitera a Slunce, uděláme tím totiž velice malou chybu.
Právě zmíněné je důvod, proč „Jupiter obíhá kolem těžiště“ zatímco Země ne. Ve skutečnosti ani jedno těleso v soustavě Slunce-Jupiter-Země neobíhá kolem těžiště, nicméně chyba, kterou takovým předpokladem uděláme, je diametrálně odlišná v případě Jupitera a v případě Země. Zatímco v případě Jupitera je tato chyba velice malá, takže představa, že Jupiter obíhá kolem společného těžiště funguje jako velice přesná aproximace, tak v případě Země uděláme chybu o dva řády větší, než jakou uděláme, pokud předpokládáme, že Země obíhá kolem středu Slunce. Příčina, proč je rozdíl mezi těmito chybami pro Jupiter a Zemi tak obrovský, tkví převážně v ohromném nesouladu mezi hmotnostmi Slunce, Jupitera a Země, nicméně nezanedbatelnou roli hraje i poměr vzdáleností mezi těmito tělesy, kdy Jupiter je pětkrát dále od Slunce než Země.
Takže pane Florian, máte ještě nějaké další pochybnosti ohledně toho těžiště? Mohu už Vás poprosit o smazání oné ostudné věty z toho pdfka, nebo aspoň o erratum k němu? :-) Každopádně za tvrzení, že Země obíhá kolem těžiště sluneční soustavy by student u zkoušky z nebeské mechaniky vylítnul jako namydlený blesk, o tom nepochybujte :-)
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz, nehezké bludy nebeské
Josef Hrncirik,2016-11-28 07:18:50
Pokud by Země obíhala kolem barycentra, v polohách jednou před Sluncem a podruhé za Sluncem, vzdálenost ke Slunci by byla cca? 150,7 Mkm či 140,3 Mkm.
Pro tento poměr vzdáleností cca 1,01 by se ozáření Země měnilo až o cca 2% tj. straším-li o, 1635 * 0,02 = cca 37 W/m2. V zásadě asi s periodou oběhu Jupitera ? cca. 11 let eventuálně interferující s periodami Saturnu. Docházelo by pak k vysokým a rychlým změnám ozáření Země. To by určitě neumiklo již Milankovičovi a bylo by to naměřeno již na Zemi i z družic.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz, nehezké bludy nebeské
Josef Hrncirik,2016-11-28 14:51:51
Šotku, už žádné poruchy!
Místo 140,3 Mkm tam vrať nazpět 149,3 Mkm!
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz, nehezké bludy nebeské
Pavel Brož,2016-11-28 15:28:54
Ano, máte pravdu v tom (pouze numericky mi to vyšlo jinak), že pokud by Země obíhala kolem těžiště sluneční soustavy, tak by se hodnota jejího maximálního i minimálního přiblížení ke Slunci co šest let měnila o 2*716330=1432660 km, což je zhruba setina AU. Správně uvádíte, že jedna extrémní hodnota by nastala když by Země-Slunce-Jupiter byly v přímce (v uvedeném pořadí), tj. těžiště by bylo o 716330 km dále od Země než střed Slunce. Druhá extrémní hodnota by nastala o šest let později, kdy by tyto tři planety byly opět v přímce, nyní ovšem v pořadí Jupiter-Země-Slunce, tj. těžiště by bylo naopak o 716330 km blíže k Zemi než střed Slunce.
Pokud by Země obíhala zhruba po elipse s těžištěm v ohnisku místo se středem Slunce v ohnisku, tak by nejbližší přiblížení Země ke Slunci nastalo při vzdálenosti o 1432660 km menší, než o šest let později. A samozřejmě s půlročním zpožděním by totéž platilo o největším vzdálení Země od Slunce, to by taky variovalo o těch 1432660 km za šest let. Jenže to se neděje, resp. ne v tomto měřítku. Nejbližší přiblížení Země ke Slunci sice variuje s tou zhruba šestiletou periodou, ale o hodnotu o dva řády menší.
Díky změnám excentricity v periodě zhruba 100000 let se sice perihelium mění dokonce o šestkrát větší hodnotu než je zmíněných 1432660 km - jenže to se děje ne s tou šestiletou periodou, ale se stotisícletou periodou. V současné epoše tedy máme hodnotu nejbližšího přiblížení Země ke středu Slunce cca 147095000 km, a tato hodnota se opravdu nemění co šest let o zhruba jedno procento.
Rád bych jenom zdůraznil pro případné čtenáře, kteří by si celý ten spor možná mohli vyložit jako spor o to, kde umístit počátek souřadné soustavy. Ne, o to se tady nejedná. Počátek souřadné soustavy si můžeme umístit kde chceme, můžeme si klidně vybrat, jestli ho umístíme do těžiště, nebo do středu Slunce, nebo dokonce do středu Země. Co se ale při tom výběru mění, je to, nakolik "hezky" vypadají oběžné dráhy těles. Tak např. není problém popisovat pohyb planet v soustavě se Zemí v počátku - ostatně, je to velice praktické pro reálnou observační astronomii. Akorát potom dráhy planet budou z pohledu ze Země opisovat takové záhadné epicykly, se kterými se museli numericky popasovat Ptolemajovští astronomové - viz https://en.wikipedia.org/wiki/Geocentric_model#Ptolemaic_system . Neznamená to, že by tento popis byl špatný nebo dokonce nepřesný - ba naopak, Ptolemajovský systém byl za více než 1500 let jeho používání numericky nafitován tak dobře, že původní Koperníkův systém, který jej měl nahradit, zdaleka tak přesné predikce pohybu planet nedával (prostě proto, že Koperník se narodil nějaký ten pátek před Keplerem, kdyby byli současníci a pracovali synergicky, třeba by to tomu Ptolemajovskému systému od začátku nandali i co se týče přesnosti předpovědí). Přednost Koperníkova systému byla ale v tom, že do té doby složité pohyby planet na noční obloze bylo možné nově vysvětlit jako relativně jednoduché dráhy planet obíhajících kolem Slunce, které se zesložití pouze tím, že jsou nahlíženy z geocentrické soustavy.
Vraťme se nyní k tomu těžišti a drahám planet nahlíženým z toho těžiště. Tam platí, že nejhmotnější planeta, je-li její hmotnost dostatečně velká, tak obíhá s velikou přesností po elipse s těžištěm v ohnisku. Není to sice úplně přesně pravda, ale ta chyba je malá. Pro další méně hmotná tělesa už ale dostaneme chyby závislé na jejich hmotnosti a poloze. Tak např. pro měsíce Jupitera platí, že v soustavě se středem v těžišti - ale i v soustavě se středem ve středu Slunce - tyto měsíce obíhají po složitých epicyklech. Jejich dráha se překvapivě zjednoduší v "Jupitero-centrickém" systému, tedy v soustavě se středem v Jupiteru, ve které tyto měsíce obíhají po elegantních elipsách místo po drahách s mnoha kudrlinkami.
Vidíme tedy, že pro každé těleso sluneční soustavy můžeme najít jinou soustavu, ve které se její pohyb maximálně zjednoduší. Pro Jupiter to je soustava spojená s těžištěm, což je dáno tím, že Jupiter mezi planetami hmotnostně naprosto dominuje. Pro Zemi se ukazuje, že soustavou, ve které se její dráha nejvíce zjednoduší, je mnohem spíše soustava se středem ve středu Slunce spíše než soustava se středem v těžišti. To je dáno zase tím, že Jupiter, ač nejhmotnější planeta soustavy, je přece jen tisíckrát lehčí než Slunce, plus navíc je od Země vzdálen minimálně čtyřikrát dále než Slunce - obojí ve výsledku znamená to, že dráha Země je v prvé řadě determinována hlavně působením Slunce, zatímco působení Jupitera lze nahlížet jenom jako malou perturbaci (jelikož maximální gravitační síla, jakou Jupiter působí na Zemi, je jen 16 tisíckrát menší, než jakou silou působí na Zemi Slunce). Pro měsíce Jupitera je zase nejvhodnější soustavou, ve které se jejich dráhy maximálně zjednoduší, soustava se středem v Jupiteru. To je dáno tím, že při daných vzdálenostech je naopak gravitační síla Jupitera, jakou působí na své měsíce, naprosto dominantní, kdežto naopak vliv gravitační síly Slnce na jejich pohyb můžeme klidně zanedbat.
Takže o tomhletom to je. Není to o tom, že bychom si nemohli položit počátek soustavy kde budeme chtít. To samozřejmě můžeme. Jde jenom o to, jak jednoduše budou vypadat dráhy těch kterých těles v té které soustavě.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-28 14:18:18
Pro p. Brože z 28.11.
Pojem barycentrum se používá i u vícenásobných soustav, třeba Centauri. (https://cs.wikipedia.org/wiki/Trojhv%C4%9Bzda)
https://en.wikipedia.org/wiki/Barycenter
"Dvě tělesa se stejnou hmotou obíhající společné barycentrum, po excentrických eliptických oběžných drahách (společná situace dvojhvězd ). Z animovaného gifu tam : Obíhají kolem společného ohniska dvou elips.
Podobně sytém Pluto-Cháron obíhá kolem barycentra.
Planetární systém jádro Slunce, povrch Slunce a pohyb barycentra
Výňatky z Vašich úvah : Shodneme se, že dvě tělesa obíhají přsně kolem společného těžiště ( pro Zemi je to v ohnisku elipsy hluboko uvniř Slunce).
Systém Slunce- Jupiter-Země píšete :
"Před přidáním třetího tělesa to platí absolutně přesně, po přidání lehkého třetího tělesa už ne úplně přesně, protože přidáním třetího tělesa polohu těžiště maličko ovlivníme."
// ANO. ALE. Na co něco počítáme, když pracujeme s pojmy ne úplně přesně, a maličko) //
.." Třetí těleso svou malou hmotou pohyb těch dvou těžkých prakticky neovlivní, proto bude i nadále platit, že tato dvě tělesa obíhají kolem společného těžiště (v našem zadání je celkem jedno, jestli toto těžiště bereme jako těžiště pouze dvou původních těles anebo jako těžiště všech tří těles, protože obě tato těžiště budou mít téměř stejnou polohu)"
// ANO.ALE. Pojmy ..celkem jedno .. mít téměř stejnou polohu//
"Třetí těleso obíhá kolem elipsy, v jejímž ohnisku je nejtěžší těleso soustavy. Druhé nejtěžší těleso soustavy na naše třetí těleso působí maximálně tisíckrát menší silou, než to nejhmotnější těleso, jeho působení bude proto znamenat pouze velice malou poruchu k eliptickému pohybu třetího tělesa kolem toho nejhmotnějšího."
//ANO.ALE. pojem- velice malou poruchu.//
Takže hurá do pojmů trochu, nepatrně a velice málo.
Když to hodně zjednodušíme, shodneme se na tom, že Země obíhá po málo výstředné elipse kolem Slunce, které je v ohnisku této zemské elipsy. Společné těžiště Slunce-Země je hluboko uvnitř Slunce a obě tělesa obíhají vlastně kolem tohoto těžiště.
Jenomže těžiště Slunce se pohybuje po své malé dráze, která je dána gravitačním vlivem všech částí sluneční soustavy hlavně Jupitera a Saturnu. Protože Jupiter a Saturn mohou v krajních případech táhnout Slunce k sobě ( Slunce-Jupiter-Saturn) nebo proti sobě ( Jupiter-Slunce-Saturn), většinou je to ale zmateně různě mezi tím. Pohyb centra hmotnosti sluneční soustavy ( snad těžiště) ukazuje
https://upload.wikimedia.org/wikipedia/commons/thumb/0/0c/Solar_system_barycenter.svg/695px-Solar_system_barycenter.svg.png
Toto centrum hmotnosti sluneční soustavy se během pár let slušně pohybuje. Z čehož plyne že synchronně s ním se pohybuje i samo Slunce, které zbytek sluneční soustavy řeknu jednoduše vyvažuje. Motá se tedy obdobně jako barycentrum sluneční soustavy a nedaleko od něj, řádově v oblasti o velikosti jeden poloměr Slunce.
Jestliže vezmeme soustavu spojenou se středem Slunce, pak oběh Země s dobrou přesností obíhá kolem Slunce, tedy ohnisko je blízko středu Slunce.
Jestliže vezmeme soustavu spojenou s větší částí vesmíru, kde ve středu je Slunce, tak se Slunce pohybuje a pohyb ohniska elipsy Země je v oblasti pohybu barycentra sluneční soustavy.
Na klima má vliv vzdálenost Slunce-Země, takže první možnost se soustavou spojenou se Sluncem je lepší. Slunce táhne Zemi sebou při svém pohybu vlivem barycentra Sluneční soustavy. Tato vzdálenost Slunce- Země je ovlivňována působením planet( změna excentricity dráhy), hlavně Jupitera a Saturnu. Čehož důsledkem je 100 000 letý Milankovičův cyklus.
Závěr : Země neobíhá kolem barycentra sluneční soustavy, ale mele se kolem něj. Pokud sledujeme oběh Země dlouhodobě, tak barycentrum sluneční soustavy se pohybuje ( spirálovitě) a táhne Slunce i ohnisko elipsy obíhání Země sebou.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-28 14:56:46
Quiz a nebezpečný blud barocentrický
Josef Hrncirik,2016-11-28 15:25:41
Mějme 2 stejná Slunce obíhající společné barycentrum.
V jakékoliv nenulové vzdálenosti od jejich barycentra (na jejich spojnici) umístěme symetricky 2 malé tělíska a udělme jim bludně vypočtenou rychlost, aby podle bludu setrvala na kruhové dráze.
Nedojde k tomu, nutně převládne vliv Sluncí bližších podle zákona Košile bližší kabátů.
Jinak by materiál rotující v těsné blízkosti barycentra musel rotovat nesmírně rychle, s pyrotechnickými relativistickými efekty (vlastně by tam vznikla neodolatelná černá díra).
Amen.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-28 23:00:19
Pane Florian, asi se urazíte, ale když čtu Vaše další a další argumenty, tak zjišťuji, že Vaše mezery ve fyzice jsou větší, než jsem se u Vás původně domníval. Např. uvádíte obrázek pohybu "centra hmotnosti sluneční soustavy" (což není ve skutečnosti nic jiného než těžiště sluneční soustavy), kterýžto obrázek ukazuje relativní pohyb těžiště vůči Slunci, přičemž to komentujete slovy:
"Toto centrum hmotnosti sluneční soustavy se během pár let slušně pohybuje. Z čehož plyne že synchronně s ním se pohybuje i samo Slunce, které zbytek sluneční soustavy řeknu jednoduše vyvažuje. Motá se tedy obdobně jako barycentrum sluneční soustavy a nedaleko od něj, řádově v oblasti o velikosti jeden poloměr Slunce."
Ta druhá věta je v tomto kontextu typická ukázka toho, jaký máte hokej v chápání fyzikálních pohybů a jejich popisů v různých soustavách. Pokud máme na tom obrázku vyobrazen pohyb těžiště vůči Slunci, přičemž z obrázku je zřejmé, že se toto těžiště vůči Slunci pohybuje, tak co prosím Vás má znamenat ta zmatená věta: "Z čehož plyne, že synchronně s ním se pohybuje i samo Slunce, ..."? Je snad samozřejmé, že když se těleso A pohybuje vůči tělesu B, tak že se těleso B naopak pohybuje vůči tělesu A, přičemž ten pohyb je přesně opačný. Tak jakýpak "synchronní" pohyb? To snad také říkáte: "Vlak se vůči nádraží pohybuje. Z čehož plyne, že synchronně s ním se pohybuje i samo nádraží"??? Zřejmě máte mezery v chápání relativity pohybu, když tak zřejmou vlastnost dofutrováváte takovou vatou. To neuvádím proto, že bych snad až teď zjistil, že nebeské mechanice rozumíte velice mizerně, to uvádím jako ukázku, jak snadno se dají Vaše hluboké neznalosti vyhmátnout už jen na základě Vašich zmatečných popisů.
Mimochodem, kritizujete, že jsem použil slova jako „maličko“ nebo „téměř stejnou“ atd. v mých větách jako např. „Před přidáním třetího tělesa to platí absolutně přesně, po přidání lehkého třetího tělesa už ne úplně přesně, protože přidáním třetího tělesa polohu těžiště maličko ovlivníme“ anebo „v našem zadání je celkem jedno, jestli toto těžiště bereme jako těžiště pouze dvou původních těles anebo jako těžiště všech tří těles, protože obě tato těžiště budou mít téměř stejnou polohu“, jenže hodnoty těchto nepřesností jdou velice jednoduše z toho mého zadání spočíst, což jsem u Vás prvně mylně předpokládal, že zvládnete, takže ve druhém příkladu, kde už jsem na rozdíl od toho ukázkového počítal s hodnotami pro Zemi, Slunce a Jupiter, jsem tyto nepřesnosti spočetl explicitně. Mimochodem, když si tak prohlížím tuto diskuzi, tak těch výpočtů jsem tu na rozdíl od Vás zanechal celkem dost. Spočetl jsem závislost celoročního příkonu na excentricitě, což jste mylně považoval za nelehký výpočet, ve skutečnosti to byla hračka. Spočetl jsem směr výsledných gravitačních sil působených na Jupiter a Zemi pro postavení planet, ve kterém se tyto směry nejvíce odchylují od směru k těžišti. Spočetl jsem, jak velká chyba vznikne při záměně těžiště Jupitera a Slunce za těžiště Jupitera, Slunce a Země - tím pádem je naprosto jasné, jak málo ovlivníme polohu těžiště dvou původních těles (Jupitera a Slunce) přidáním třetího tělesa (Země). Připomínám, že původní poloha těžiště Jupitera a Slunce se přidáním Země ve směru kolmém ke spojnici Jupiter-Slunce změnila ze vzdálenosti 716332 km od středu Slunce na vzdálenost 716330 km a posunula od spojnice Jupiter-Slunce směrem k Zemi o pouhých 450 km. To je naprosto jednoznačné kvantitativní vyčíslení té nepřesnosti, s jakou se ovlivní původní těžiště pouze dvou těles přidáním tělesa třetího.
Všechny tyto věci by samozřejmě pro člověka byť jen s minimálními znalostmi nebeské mechaniky (ba dokonce jen se znalostmi klasické mechaniky) byly naprosto elementární a už z toho prvního příkladu by je byl schopen sám spočíst. To byl právě můj omyl, že jsem Vás napoprvé považoval za člověka disponujícími aspoň těmito minimálními znalostmi, v tom jsem se právě spletl. A jelikož Vy jste si nebyl schopen tyto elementární věci spočíst sám (přitom ten první příklad se třemi tělesy jsem koncipoval záměrně tak, aby se všechno dalo snadno spočítat z hlavy bez nutnosti použít papír a pero), tak holt argumentujete „hurá do pojmů trochu, nepatrně a velice málo“.
To je další indicie Vašeho fyzikálního diletantismu. Dostanete učebnicově jednoduchý příklad, ale nejste schopen ho pochopit. Takže nejprve mlžíte ohledně umělosti předpokladů. Dobrá, spočítal jsem Vám tedy explicitně druhý příklad, pro konkrétní hodnoty pro Jupiter, Slunce a Zemi. Opět nejste schopen ho pochopit, o čemž mj. svědčí Vaše věty:
„Jupiter oběhne za 12 let. Za 6 let bude sestava podle hodin Jupiter na 3, Země zase na 6 a Slunce uprostřed. Pracně vypočítaná odchylka bude přesně opačná a její součet přesně nulový, ne nulový jako, že jsme něco zaokrouhlili. Tedy těžiště pro tato dvě krajní možnosti soustavy bude uprostřed Slunce.“
Odkdy se při výpočtu tvaru oběžných drah těles majících zadanou dobu oběhu (konkrétně pro výpočet tvaru dráhy Země obíhajících s periodou jeden rok) provádí průměrování přes násobně delší dobu (ve Vaší argumentaci jde o dobu 6 let, kdy se změní pozice těžiště vůči středu Slunce na opačnou)? Když bych tento Váš „princip“ použil třeba na výpočet tvaru drah Jupiterových měsíců v heliocentrické soustavě, a zprůměroval jejich dráhu přes dvanáct let, za kterou oběhne Jupiter kolem Slunce, tak by mi vyšlo, že místo po epicyklech, po kterých v této soustavě opravdu obíhají, by měly obíhat po krásných hladkých elipsách, v důsledku toho průměrování prakticky identických s drahou Jupitera. Podobné průměrování se dá použít pouze v naprosto odlišném případě, když síla působící na sledované těleso osciluje s periodou mnohem kratší, než je perioda oběhu tělesa, jehož dráhu vyšetřujeme. Tak např. když by velmi vzdálená planeta obíhala kolem těsné dvojhvězdy, kdy by oběžná doba té planety byla např. stokrát delší než oběžná doba těch hvězd kolem sebe. Ano, v tomto případě bychom mohli udělat časové zprůměrování sil jakými tyto hvězdy působí na planetu, a dráha planety vypočtená pomocí tohoto časového průměru by byla prakticky stejná, jako dráha, kterou bychom spočetli přesně např. s pomocí počítače. Ale myslet si, že to platí obráceně, že toto průměrování můžeme udělat i v případě, kdy nám jde o tvar dráhy Země s oběžnou dobou jeden rok, a vypočítáváme průměr polohy těžiště sluneční soustavy za 6 let ... Pane Florian, pokud jste vystudoval nějaký fyzikální obor na vysoké škole, tak čestným řešením by mělo být ve Vašem případě snad asi vrácení diplomu. Protože člověk s vysokoškolským fyzikálním vzděláním by se takových lapsů dopouštět neměl, anebo ještě jinak řečeno, úroveň Vámi prezentovaných znalostí je pro Vaši alma mater velice špatnou vizitkou.
Takhle bych mohl pokračovat dlouho, protože co Vaše druhá až třetí věta, to perla. Celkem rozumím Vaší zálibě v odkazování na všemožné ty klimatologické grafy, ono k nim není potřeba umět nic hodnověrně spočítat, stačí na ně odkazovat a dokola tvrdit, jak je na nich evidentně patrné, že toto přece nutně koreluje s tímto ... Bezesporu mnohem snazší, než něco reálně vypočítat, natožpak něčemu pořádně rozumět.
A to je také jádro mého zásadního skepticismu jak vůči klimaskeptikům, tak vůči klamalarmistům. Obě dvě skupiny vědců kolem sebe nabalují fankluby lidí, jako jste Vy, tedy lidí s velice děravými fyzikálními znalostmi, přičemž tady se nebavíme o mezerách ve znalostech např. kosmologie, kvantové mechaniky či fyziky elementárních částic, kteréžto obory nejsou pro klimatologii klíčové, ale bavíme se zde o mezerách v tak základních oborech, jako je nebeská mechanika. Aby to nevypadalo, že kritizuji jenom Vás coby představitele fanklubu jedné strany, různá fantastická tvrzení jsem si přečetl taky od pana Kremlíka v diskuzi zde: http://www.osel.cz/5708-za-klimatickymi-zmenami-muze-byt-pohyb-slunce.html . Musím říct, že tam jsem se přímo královsky bavil.
Ostatním čtenářům můžu doporučit totéž. Nenechte se ohlupovat ani jednou stranou toho sporu. Je snadné sklouznout do jednoho z těch fanklubů a časem vyměnit vlastní kritické uvažování za ideologické teze svého domácího tábora. Časem pak zapomenete na to, že spoustu věcí si můžete po osvěžení svých elementárních fyzikálních znalostí spočíst sami, a místo toho se z vás stanou sběratelé grafů. A pokud se pak přistihnete, že místo racionálních argumentů odkazujete na nějaké grafy s tvrzením, že tam ty korelace jsou přece jasně vidět místo toho abyste své tvrzení podložili výpočtem, tak potom budete vědět, že jste na tom co se týče fyziky velice špatně.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-29 01:43:35
Pane Broži, klídek, nejsem Váš žák. Článek je o klimatu. Klima je výsledek dlouhodobého působení počasí. Oběh Jupitera je za 12 let, a jde o doby ledové s periodou 100 000 let. Za 12 let oběhu Jupitera se účinky Vašeho posledního vzorového výpočtu vyrovnají na nulu. Takže mi dovolte pochybovat i o dalších klimatických dopadech Vašich výpočtů, například, že energie dodaná Sluncem Zemi nezávisí na excentricitě, což mnou mnohokrát uvedené grafy z Wikipedie právě ukazují stejně jako vysvětlení hesla Milankovičovvy cykly.
Díval jsem se na graf z následujícího odkazu, kde se řeší jmenovitě pohyb Slunce jako protipohyb zbytku sluneční soustavy
https://www.geogebra.org/m/h78WaaR2
"Výpočty prokázaly, že Slunce se pohybuje v oblasti o průměru 4,3 slunečních poloměrů, respektive 3 mil. km, což opravdu není „zanedbatelná“ hodnota – představuje 8x větší míru, nežli je vzdálenost ze Země na Měsíc! "
Ale jak píšete jsem diskutér skoro nepočítající a s mezerami ve fyzice a nebeské mechanice. To je jedna z věcí, kde máte opravdu jasno.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-29 10:37:13
Pro Pavel Brož,2016-11-28 23:00:19
http://www.osel.cz/5708-za-klimatickymi-zmenami-muze-byt-pohyb-slunce.html
Charvátová, z Geofyzikálního ústavu AV ČR odpovídá na:
//Vy se v Geofyzikálním ústavu zabýváte inerciálním pohybem Slunce. Anglicky SIM (Solar Inertial Motion). Můžete říci, co to je?//
"To je pohyb Slunce kolem těžiště (barycentra) slunečního systému, který je dán proměňujícím se rozložením planet, především planet obřích...Slunce se pohybuje v oblasti o průměru 4,3 slunečních poloměrů, tj. 0,02 AU nebo 3 milionů km. "
Závěry odtud Charvátové a Kremlíka směrem k dlohodobému klimatu považuji za špatné a obecně souhlasím s Vámi, že změny magnetismu a dopady na klima jsou velmi malé.
Můj závěr : Pohyb Slunce kolem těžiště ( barycentra) slunečního systému existuje, což plyne i z obrázku
http://upload.wikimedia.org/wikipedia/commons/thumb/0/0c/Solar_system_barycenter.svg/440px-Solar_system_barycenter.svg.png
Pohyb těžiště sluneční soustavy kolem Slunce a jeho jádra. Slunce se nepohybuje v soustavě spojené s jejím středem, pohybuje se v soustavě spojené s barycentrem sluneční soustavy. Pohyb a klid je relativní a neznalosti fyziky, které jsem tímto údajně prokázal, rovněž. Můžeme mít i soustavu, kde se pohybuje Slunce i těžiště sluneční soustavy, což pro pochopení tohoto jevu je názorné. Ale musí se chtít to pochopit, což se Vám nepodařilo kvůli rozboru mých neschopností.
Nejsem uražený, prostě považuji pojem barycentra při vysvětlení pohybů ve sluneční soustavě za užitečné.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-29 18:58:21
Pane Florian, pojem barycentra neboli česky těžiště je pojmem opravdu velice užitečným, v tom máte bezesporu pravdu a to opravdu nerozporuju. Těžiště jakékoliv izolované soustavy, za jakou lze s velikou přesností považovat i sluneční soustavu, má totiž tu úžasnou vlastnost že soustava s ním spjatá je inerciální. Tím pádem v jakékoliv inerciální soustavě se těžiště pohybuje rovnoměrně přímočaře. Což třeba o středu Slunce, ani o středu Země, ani o středu jakéhokoliv jiného tělesa ve sluneční soustavě říci nemůžeme - všechny tyto body se v inerciálních soustavách pohybují s nenulovým zrychlením.
Těžiště má i další výhodné vlastnosti, takže se s oblibou používá jakožto počátek souřadnicové soustavy, ve které se zobrazuje pohyb těles, protože např. některé veličiny se pak v takové soustavě spočítají snadněji - např. celkový moment hybnosti celé soustavy spočtete snadno tak, že v těžišťové soustavě vezmete tangenciální složky hybností těles, vynásobíte je jednotlivě jejich vzdáleností od těžiště a součiny sečtete. Kdybyste totéž udělal např. v soustavě se středem v Jupiteru, tak Vám nevyjde správná hodnota pro moment hybnosti celé sluneční soustavy.
Protože je tedy používání těžišťové soustavy tak rozšířené, vede to u nefyziků často k takové lákavé myšlenkové zkratce, že se vlastně pohyb těles ve sluneční soustavě dá představit tak, jako by ta tělesa obíhala po elipsách, akorát s ohniskem v těžišti. Ona je to navíc pravda, pokud ta tělesa jsou pouze dvě. Jenže pro více těles je to omyl, těžiště v tomto případě tuto vlastnost nemá, nemá ji už jenom z toho důvodu, že výslednice gravitačních sil, jakými na jedno sledované těleso působí ostatní tělesa, nemíří do těžiště. V případě dvou těles tam ale míří, protože z vlastnosti těžiště plyne, že pokud jsou tělesa jenom dvě, tak těžiště se nachází na jejich spojnici, a jejich spojnice je přesně ten směr gravitační síly působené druhým tělesem. V případě tří a více těles se dá ale snadno ukázat, že směr od vybraného tělesa k těžišti a směr výsledné gravitační síla působené ostatními tělesy mohou být velice odlišné. Nejlépe to může být ilustrováno třeba na měsících Jupiteru. V jejich případě míří výsledná gravitační síla prakticky do středu Jupiteru, protože Slunce na ně působí mnohem menší silou (tak např. v případě měsíce Ganymedes je gravitační síla Slunce asi 560 krát slabší než gravitační síla Jupitera). Dokonce i v případě našeho Měsíce se dá snadno ukázat, že směr výsledné gravitační síly a směr k těžišti je obecně různý – síla, jakou působí Slunce na Měsíc je sice asi 2,2 krát větší než síla, jakou na něj působí Země (důvod, proč Měsíc od Země neodletí je ten, že Země i Měsíc „padají“ v prakticky identickém gravitačním poli Slunce se stejným zrychlením), nicméně výslednice obou sil např. v první či poslední čtvrti Měsíce míří o 24,6 stupně jinam než je směr k těžišti. Mimochodem, můžeme jejich role i prohodit, a spočítat odchylku příslušných sil pro Zemi – vyjde nám, že jelikož je gravitační síla Měsíce asi 177 krát slabší než gravitační síla Slunce (neplést se slapovými silami, kde je naopak slapová síla Měsíce zhruba dvakrát větší než slapová síla Slunce, protože slapové síly jsou nepřímo úměrné třetí místo druhé mocnině vzdálenosti), tak odchylka výslednice obou sil míří v první či poslední čtvrti Měsíce o 0,32 stupně jinam než k těžišti. Odlišnost těchto dvou směrů v soustavě tří a více těles je jeden z důvodů (nikoliv ale jediný), proč tělesa ve sluneční soustavě neobíhají po elipsách s ohniskem v těžišti.
V obecné soustavě tří těles může jejich pohyb opisovat velice divoké křivky, které se elipsám ani náhodou nepodobají. Tak např. kdybychom měly tři srovnatelně těžká tělesa, ve vzdálenostech zhruba podobných (dejme bychom zvolili počáteční vzdálenost prvých dvou jako etalon, přičemž počáteční vzdálenost třetího od prvého by byla jedenapůlnásobkem a vzdálenost třetího od druhého dvounásobkem), a udělili jim vůči jejich těžišti pouze tangenciální počáteční rychlosti, tak výsledný pohyb bude velice chaotický. Podobné příklady se třemi tělesy se mimochodem s oblibou studují v rámci teorie deterministického chaosu. Obecný problém tří těles je neřešitelný exaktně, protože se dá matematicky dokázat, že neexistuje žádný výraz vytvořený pomocí konečného použití elementárních funkcí (jako třeba cos, sin, exp, log, atd. atd.) a konečného použití integrálů a derivací, pomocí kterého by se dala vyjádřit dráha jednotlivých těles (to je rozdíl od problému pouze dvou těles, který se exaktně řešit dá, a dráha dvou gravitačně vázaných těles vyjde jako elipsa, v jejímž ohnisku je těžiště těchto dvou těles). Obecný problém tří těles se v praxi nedá moc dobře řešit ani numericky, a to proto, že počáteční nepřesnosti v zadaných polohách a hybnostech se pro určité oblasti hodnot těchto poloh a hybností mají tendenci exponenciálně zvětšovat. Tzn. že když vybereme nějaké obecné počáteční podmínky, tak už po několika desítkách oběhů tří těles dostaneme většinou zcela zcestné numerické předpovědi, a to nejméně dvou důvodů - jednak reálně máme možnost zadat počáteční polohy a hybnosti s nějakou nenulovou přesností, a jednak hodnoty průběžně vypočítávaných čísel nepočítáme s přesností na nekonečně mnoho desetinných míst, takže nám zde nutně vznikají zaokrouhlovací chyby. To vede k tomu, že pokud se nacházíme v oblasti počátečních hodnot, pro kterou se odchylky skutečných drah exponenciálně zvětšují, tak numerická simulace problému tří těles může být použitelná jenom po dobu několika desítek oběhů, potom už je úplně mimo. Pro obecný problém pohybu více než tří těles samozřejmě platí totéž - při obecných podmínkách dostaneme dráhy, které se elipsám neblíží ani vzdáleně, přičemž během tohoto pohybu je nezřídka některé z těles úplně vystřeleno pryč z celé soustavy, tj. s rychlostí větší než únikovou, takže už se nikdy nevrátí.
Naše sluneční soustava naštěstí není soustavou, ve které by se pohybovala tělesa srovnatelných hmotností ve srovnatelných vzdálenostech (pokud teda pomineme např. pás planetek mezi Marsem a Jupiterem, jejichž pohyb se dá spolehlivě předpovídat jenom na pár desítek oběhů či ještě méně). V důsledku předpokládaného mechanismu jejího vzniku a v důsledku chaotické selekce protoplanet v jejím raném období nám tady v současné době zůstal relativně velice stabilní systém, který má daleko do typické soustavy popisované deterministicky-chaotickými modely. Jenom díky tomu, že vzdálenosti planet od sebe navzájem jsou velice velké a že jejich hmotnosti vůči hmotnosti Slunce jsou o více než tři řády menší, tak jedině díky tomu můžeme s úspěchem použít poruchovou metodu nebeské mechaniky, ve které jako výchozí aproximaci uvažujeme, že jedinou silou působící v soustavě je gravitační síla Slunce (zatímco vzájemné gravitační síly planet na sebe zanedbáme), a teprve v dalších přiblíženích uvažujeme vzájemné gravitační síly planet jakožto poruchy, přičemž i tyto jednotlivé síly můžeme krok za krokem aproximovat (tj. sílu další započítané planety nemusíme přidat v jednom kroku, můžeme ji přidat v několika postupných aproximacích, kdy nejprve např. přidáme její homogenní část a spočteme jí odpovídající korekci, potom nehomogenní část, atd.). Jelikož ve výchozí aproximaci uvažujeme planety jakožto navzájem neinteragující tělesa pohybující se pouze pod vlivem gravitačního pole Slunce, tak výchozím pohybem planet bude pohyb po elipsách s ohniskem ve Slunci. Další přiblížení jsou postupné korekce k tomuto pohybu.
Poruchová metoda v nebeské mechanice je velice silný nástroj pro počítání a předpovídání pohybu planet. Její základní myšlenkou – jako u každé jiné poruchové metody – je, že celkové komplikované silové působení těles ve sluneční soustavě se rozloží do řady aproximací, v níž každá další aproximace dá řádově menší korekci než aproximace předchozí. Díky tomu tato řada konverguje a lze se s ní dopočítat k dostatečně přesným výsledkům. Právě poruchová metoda umožnila prvním astronomům po Newtonovi úspěšně předpovídat návraty komet či objevovat další planety a planetky sluneční soustavy, a to všechno bez existence počítačů.
Můžu klidně ukázat, jak se dá i bez počítačů postupnými aproximacemi vydolovávat krok za krokem informace o skutečném tvaru dráhy Země při pohybu kolem Slunce se zohledněním vlivu Jupitera, akorát by to bylo opravdu dlouhé.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Josef Hrncirik,2016-11-29 21:02:33
Mistře díky za opravu slunečních hodin a Ptolemaiova orloje.
Zaúčtujte si to prosím do úvazku jako 10 hodin doučování repetentů.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-29 21:04:51
Pro P. Bože, z 29.11.
Dobře. Nikdy jsme si nemyslel, že pohyb planet je jednoduchý, máme astronomy, kteří dokáží své výpočty uspořádat do grafů a výsledky podpořit měřením (třeba stáčení perihélia Merkuru podle teorie relativity nebude asi taky nic jednoduchého, ale potvrzeno to je). Dokáží spočítat polohu planet s takovou přesností, že je můžou zasáhnout nebo obíhat sondy. Není důvod jim nevěřit. Jinak slušně řečeno výpočty matematicky správné, ale vytržené ze souvislostí jsou celkem k ničemu.
Závěr je opravdu jednoduchý.
1)Země obíhá po málo výstřední elipse kolem Slunce (kolem bodu blízko jeho středu.
2)Slunce obíhá kolem barycentra ( těžiště) sluneční soustavy.
Obíhá spirálovitě a rychlostí asi 50 km/h, což není ve sluneční soustavě moc. A křivky tohoto oběhu, respektive pohybu barycentra kolem jádra Slunce v soustavě spojené s jádrem Slunce jsou spočteny a vyneseny do grafů.
Zdá se jasné, že model planet se Sluncem ve společném ohnisku elips oběhu planet a souřadnicovou soustavou ve středu Slunce je postačující. Ve středu i ve čtvrtek.
ANO. Až na to, že odchylky (hlavně vlivem Jupitera a Saturnu) vyvolávají 100 000 letý Milankovičův cyklus, který je v příčinné souvislosti s dobami ledovými.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-29 22:41:55
Myslím, že teď už se skoro stoprocentně shodneme s jednou jedinou výjimkou:
Váš závěr číslo 1) - v tomto se naprosto shodneme
Váš závěr číslo 2) - ano, i v tomto se úplně shodneme
a dokonce i s následujícími dvěma větami.
Pouze s tou větou "Zdá se jasné, že model planet se Sluncem ve společném ohnisku elips oběhu planet a souřadnicovou soustavou ve středu Slunce je postačující." nemůžu zcela souhlasit, protože dostatečně přesně platí pro planety typu Země, Merkur, Venuše a Mars, ale třeba pro ten Jupiter je opravdu mnohem přesnější model, kdy obíhá kolem elipsy s ohniskem v těžišti nikoliv s ohniskem ve středu Slunce, a dokonce tentýž model s ohniskem v těžišti o něco lépe vyhovuje všem dalším vnějším planetám, bez ohledu na jejich hmotnost. Důvodem je délka oběžných dob a rozdělení hmotností těles v závislosti na jejich pořadí od Slunce. První čtyři planety jsou příliš lehké na to, než aby svou hmotností nějak podstatně ovlivnily polohu těžiště celé soustavy, které je dominantně určeno Jupiterem. Zároveň tyto planety obíhají blíže než Jupiter, tedy jejich oběžné doby jsou kratší - v případě Merkuru cca 50 krát, v případě Venuše 19 krát, v případě Země skoro 12 krát, v případě Marsu cca 6 krát. Výsledná gravitační síla na ně působící míří s velikou přesností do středu Slunce, proto pro ně s uspokojivou přesností platí, že obíhají kolem bodu blízko středu Slunce. Další v pořadí od Slunce je Jupiter, a zde nastává kvalitativní změna - Jupiter nejpodstatněji ze všech planet sluneční soustavy ovlivňuje polohu těžiště. Zatímco zpětný vliv prvních čtyř planet na pohyb Slunce šlo velice dobře zanedbat (protože např. Země má cca 333000 krát menší hmotnost než Slunce), tak u Jupitera toto zanedbání udělat nemůžeme. Jupiter je už zkrátka dost macatý na to, aby i to velké a těžké Slunce při svém oběhu vychyloval o ten plus minus poloměr Slunce - na něco takového ty první čtyři planety zkrátka nemají. Zároveň je ale oběžná doba Jupitera násobněkrát delší než oběžná doba těch prvních čtyř planet, a proto tyto se během svého oběhu stíhají adaptovat. Jupiter je na jejich poměry zkrátka příliš pomalý, jeho vliv se projeví tak, že elipsy těch vnitřních planet se budou jako celek cyklicky posouvat s periodou těch dvanáct let. Prostě jako kdybychom ty čtyři elipsy nakreslili na papír spolu se Slunce v jejich ohnisku (ve skutečnosti ne úplně přesně, protože pro každou elipsu by to ohnisko bylo maliličko jinde a měnilo by se s dobou oběhu té které planety) a pak bychom na ten papír položili dlaň a maličko zakroužili dlaní po podložce. Toto je možné jenom protože je ten Jupiter tak pomalý a zároveň tak hmotný ve srovnání s ostatními planetami.
Podívejme se nyní na Neptun jakožto nejvzdálenější vnější planetu. Jupiter na něj působí i v místě jejich největšího přiblížení asi 27 krát slabší gravitační silou, než Slunce, tedy Slunce je pro pohyb Neptunu dominantní (i když poruchy působené Jupiterem už rozhodně nejsou slabé). Díky tomu, že oběžná doba Neptunu je skoro 165 let, tedy cca 14 krát delší než oběžná dráha Jupitera, tak se gravitační síla Slunce za tu dobu velice slušně vystředuje - Slunce zkrátka za jeden oběh Neptuna oběhne skoro 14 krát kolem těžiště sluneční soustavy. Pokud k pohybu těžiště připočteme vliv i Saturnu a Uranu, tak to průměrování bude delší, protože Slunce kolem těžiště pak neoběhne po dokonalé kružnici, ale po složitější růžici, nicméně i pak pořád bude platit, že během oběhu Neptunu se gravitační síla Slunce se slušnou přesností zprůměruje, jako kdyby efektivně sedělo v tom těžišti.
Tzn. že zatímco pro první čtyři planety je Jupiter (a tím i pohyb Slunce kolem těžiště) příliš pomalý, takže tyto se během svých oběhů stíhají se svými dráhami adaptovat na pomalu se pohybující Slunce, tak pro Neptun je naopak Jupiter (a tím i pohyb Slunce kolem těžiště) příliš rychlý, takže ve výsledku mu díky tomu vystředování spíše vyhovuje to těžiště v ohnisku.
Ve skutečnosti ale pro vnější planety za Jupiterem, tedy pro Saturn, Uran a Neptun, už je tato debata pouze akademická, a to z toho důvodu, že odchylky tvaru jejich drah od elipsy už jsou v důsledku nezanedbatelných poruch působených zejména Jupiterem natolik velké, že pohyb Slunce kolem těžiště už je ve srovnání s tím detail. Bavit se o elipse a jeho ohnisku s takovouto přesností už zkrátka nedává moc smysl, když ty dráhy jsou bramborovatější o dost více, než je vzdálenost Slunce k ohnisku. Proto má smysl se o tomto bavit ještě u Jupitera, jehož dráha je vzhledem k jeho hmotnosti ještě s dostatečnou přesností eliptická.
Každopádně důvodem té "kvalitativní" změny toho oběhu je právě distribuce hmotností planet v pořadí od Slunce: hmotnosti jsou nic, nic, nic, nic, 72%, 31%, 3,2%, 3,8%. Právě u těch 72%, tedy u Jupitera, už s velkou přesností platí, že obíhá s těžištěm sluneční soustavy v ohnisku, zatímco u těch prvních čtyř nic platí, že obíhají se Sluncem v ohnisku.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Pavel Brož,2016-11-29 22:57:59
teď koukám že jsem se usekl s poměrem gravitační síly působící na Neptun - má být "Jupiter na něj působí i v místě jejich největšího přiblížení asi 700 krát slabší gravitační silou, než Slunce". To je tím, když se u toho psaní zároveň koukám na televizi :-) Naštěstí jsem konkrétní hodnotu toho údaje v dalších závěrech nepotřeboval, ty proto zůstávají beze změny.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Milan Krnic,2016-11-30 07:44:07
Třeba stáčení perihelia Merkuru potvrzeno je, ale o kolik nikoli.
Obdobě s počítám polohy planet, kdy tak jednoduché, jak navozujete, to není. Trasu sond korelujeme ze Země.
Michal Křížek - Problém N těles (KS ČAS 12.9.2016)
https://www.youtube.com/watch?v=JUa__7UjSVg
Analogicky s klimatem. Science magic :)
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-28 19:43:31
Pavel Brož,2016-11-28 00:26:52
https://en.wikipedia.org/wiki/Milankovitch_cycles
Zemská výstřednost se liší především v důsledku interakce s gravitačními poli Jupiteru a Saturnu . Jak se výstřednost dráhy vyvíjí, tak hlavní poloosa na orbitální elipsy zůstává beze změny. Podle třetího Keplerova zákona doba dráhy je určena hlavní poloosou. Z toho vyplývá, že oběžná doba Země, délka hvězdného roku, zůstává nezměněna..
Relativní nárůst slunečního záření za největšího přiblížení ke Slunci ( perihélium ) v porovnání s ozářením v nejvzdálenějším ( apolehélium) je o něco větší než čtyřnásobek výstřednosti. Pro aktuální okružní výstřednosti to představuje změnu v příchozí slunečního záření asi 6,8%, zatímco aktuální rozdíl mezi afélium je pouze 3,4% (milionů 5.1 km ). Když je oběžná dráha je nejvíce eliptická, množství slunečního záření u perihélia je asi o 23% více, než u apohélia."
Pozn.: Takže hodnota rozdílu ozáření apohélium a perihélium (od dneška do úplného poklesu excentricity asi za 25 000 let), kterou jsem dříve uváděl asi jako 9%, je rozumná.
Píšete jako závěr srozumitelného výpočtu :
"Představa, že Země obíhá kolem těžiště sluneční soustavy, je naprosto zcestná. Země totiž s mnohem větší přesností obíhá kolem středu Slunce – neplatí to samozřejmě přesně, ale chyba, kterou uděláme, je o dva řády nižší než chyba, kterou vytvoříme při předpokladu, že Země obíhá kolem těžiště sluneční soustavy."
Tento výpočet jako skoro všechno, co tu počítáte, je založen na nějakém výchozím předpokladu, který sedí vedle až leží vedle. Zde předpoklad je, že Jupiter-Slunce a Země tvoří na dráze pravoúhlý trojúhelník s pravým úhlem u Slunce. Podle hodin řekněme Jupiter na 9, Země na 6, Slunce uprostřed.
A kde soudruzi z NDR udělali chybu ?
Jupiter oběhne za 12 let. Za 6 let bude sestava podle hodin Jupiter na 3, Země zase na 6 a Slunce uprostřed. Pracně vypočítaná odchylka bude přesně opačná a její součet přesně nulový, ne nulový jako, že jsme něco zaokrouhlili. Tedy těžiště pro tato dvě krajní možnosti soustavy bude uprostřed Slunce. Jenže dráhy jsou eliptické, doba oběhu Jupitera není přesně 12 let a ekliptiky jsou mírně stočené, takže mnoho dalších vedlejších vlivů časově proměnných.
Výpočet jak namydlený blesk a zošmykol, upadol.
Na volbě soustavy jistě nezáleží. Zjednodušení jsou nutná.
ALE. Když můžeme najednou v pohodě sčítat celkévé silové působení Slunce a Jupitera na Zemi, proč to nemůžeme udělat obecně a řešit silové působení na Zemi od celého planetárního systému, který charakterizuje barycentrum sluneční soustavy. Ano, barycentrum se pohybuje se podle grafu
https://upload.wikimedia.org/wikipedia/commons/thumb/0/0c/Solar_system_barycenter.svg/695px-Solar_system_barycenter.svg.png
ale to se Slunce pohybuje také jako protiváha celého zbytku solární soustavy. Velikost Slunce v grafu je pro srovnání velikosti dráhy barycentra za pár desetiletí, střed Slunce se motá do spirály v tomto období stejným způsobem.
Obíhá Země kolem Slunce nebo kolem barycentra sluneční soustavy? Můžeme o tom diskutovat a to je tak všechno, co s tím můžeme dělat.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Stanislav Florian,2016-11-27 19:32:08
k Pavel Brož,2016-11-26 21:10:50
https://en.wikipedia.org/wiki/Dole_effect
k https://en.wikipedia.org/wiki/100,000-year_problem
ze 100 000 let problému
Doleův efekt.
Píše, že poměr 18O a 16O ovlivní fotosyntéza. Ale fotosyntézu ovlivní hodně věcí včetně ppm CO2. Jenže bentonitové usazeniny a poměr isotopů v nich je kromě toho časově ovlivněn tím, že USAZENIY se usazují geologicky dlouho, tedy nelze očekávat tak rychlé změny isotopů jako reakce na změny teploty jako u ledovcových jader.
Ostatně nižší hodnoty oteplování podle usazenin z amerických jezer podle McIntyra se považují všeobecně za lokální a nelze je aplikovat na globální teploty.To uznal ( prý) i sám kdysi miláček klimaskeptiků McIntyr.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Quiz
Milan Krnic,2016-11-28 18:59:16
Ono každé měření je lokální, a tedy nelze aplikovat na globální teploty. Tedy lze, s chybou, která musí být stanovena. A to, kupodivu, zcela nezávisle na ideologickém smýšlení člověka.
Drobné poruchy nekonečně se opakujících nesporných důkazů nekonečnými spory.
Josef Hrncirik,2016-11-24 07:03:59
Zdá se, že při kruhové dráze, tj. když zákonitě náhodou jsou v konjukci nejen numerická, ale dokonce i absolutní excentricita, pak bez konce hlavních, tj. i vedlejších poloos udržuje svoji invariantnost, dokud v poruchách nenastane porucha.
Data
Alexandr Kostka,2016-11-21 20:37:42
Osobně bych viděl drobný zádrhel i v metodě sběru dat. Neruším jak satelitní, ale data pozemních stanic se upravují, "aby se odečetl vliv okolní výstavby", což je například u Klementina v centru milionového města dost ujetzost, protože tam si "přírodní" počasí moc neškrtne a naopak okolní výstavba ovlivňuje naprosto vše. Dle mého názoru, když se setkají upravená data z města s naměřenými hodnotami někde na větrné hůrce, tak z toho vzejde tak leda maglajs a ne použitelné údaje.
oteplování
Stanislav Florian,2016-11-21 10:35:36
Politici říkají, co se hodí. Kliamatologové tvrdí, že primární je nárůst ppm CO2 hodně ovlivněný antropogenními emisemi.
Jistě, z teplého oceánu se uvolní CO2 a ten kladnou zpětnou vazbou ovlivní zvýšení teploty. A co ohřeje oceán? Primárně energie ze Slunce, kdy se díky zvýšenému skleníkovému jevu v atmosféře pohltí více infračerveného záření. Stoupá ppm CO2 a stoupající teplota je v příčinné souvilosti s ppm CO2.
Proč po velmi teplém roce 1998, kdy se uvolnilo velké množství CO2 z oceánů do atmosféry se vůbec roku 1999 ochladilo, když podle autora článku podstatný je pro nárůst teploty podstatný předchozí teplý rok a nárůstem CO2.
Článek :"Některý rok přibude 2 ppm ( CO2) ročně a jindy třeba 2,5 ppm.
Závisí to na teplotě oceánu v předchozích měsících."
Jistě, závisí to na teplotě oceánů. Je to logika asi jako když mám na plotně hrnec s vodou a z ní jdou bublinky. Příčinou bublinek není teplý hrnec, ale plotna, která dodává energii.
http://www.esrl.noaa.gov/gmd/aggi/aggi.html.
http://www.esrl.noaa.gov/gmd/aggi/aggi.fig4_med.png
http://www.drroyspencer.com/wp-content/uploads/UAH_LT_1979_thru_October_2016_v6-550x318.gif
/ teploty podle UAH satellite a 13 měsíční klouzavý průměr, tento průměr narostl od 1979 asi o 1°C/
https://www.ncdc.noaa.gov/sotc/service/global/global-land-ocean-mntp-anom/201501-201512.png
Globální teploty podle NOAA rostou, teplota narostla od roku 1979 asi o 0,6°C.
Jestliže jsou správná málo rostoucí satelitní měření teploty, tak se těžko vysvětlí trvalý masivní úbytek ledu Arktidy a tání ( naprosté většiny) horských ledovců.
Re: oteplování
Milan Krnic,2016-11-21 11:08:36
Máte pravdu, že se těžko vysvětlí. Takhle to holt z pohledu lidí na makro úrovni našeho komplexního Vesmíru chodí.
Re: oteplování
Michal Lichvár,2016-11-21 11:25:45
"Proč po velmi teplém roce 1998, kdy se uvolnilo velké množství CO2 z oceánů do atmosféry se vůbec roku 1999 ochladilo"
... no pretoze teplota nezavisi na CO2, ale CO2 zavisi na teplote.
NOAA asi nebude zrovna vierohodny zdroj, vid graf 3,4,5. Graf 4 je od NOAA a hodnoty su zjavne vyfabulovane.
Ja sa divim, ze im to seriozne vedecky casopisy neotrepali o hlavu, kedze sa hodnoty vyrazne lisia od nameranych hodnot zo satelitov. Lenze granty a politika :-/
Co sa tyka klesajuceho zaladnenia, kludne mozme povedat, ze sa stale vynorujeme z malej doby ladovej. Konieckoncov nazov Greenland vznikol podla zelenych pastvin pri osidleni Vikingami v r.1000.
"To investigate the possibility of climatic cooling, scientists drilled into the Greenland ice caps to obtain core samples. The oxygen isotopes from the ice caps suggested that the Medieval Warm Period had caused a relatively milder climate in Greenland, lasting from roughly 800 to 1200. However, from 1300 or so the climate began to cool. By 1420, the "Little Ice Age" had reached intense levels in Greenland.[15]"
https://en.wikipedia.org/wiki/History_of_Greenland
Ja ako furt neviem, co za pohromu ma byt globalne oteplenie. Teplo uvolnuje CO2 z atmosfery, vdaka comu su vacsie vynosi polnohospodarstva. Teplo znamena viac vody v atmosfere, cize viac zrazok a menej such. Ak su zrazky silnejsie, je to len preto, ze prilis odlesnujeme (lesy su ako spongia).
Naproti tomu pri globalnom ochladeni - postupujuce ladovce trvalo nicia ludske osidlenia ... je menej vlhokosti, vacsie sucha, nizsie urody => tlak na ludsku spolocnost => vojny. Podotykam ze 100rocna vojna bola v case globalneho ochladenia.
Jaj a co sa tyka topenia ladovcov ... aj satelitne merania ukazuju, ze najsilnejsie oteplenie je prave v istej casti Akrtidy. Cize mozno preto sa topia viac, ako rastie globalna teplota.
A ako ste pisali, pricinou bublinek neni teply hrec, ale plotna ... v tomto pripade mame dve plotny ... jednu dole (zemske jadro) a druhu hore (Slnko). A mna by napr. velmi zaujimalo, ako velmi slapove sily Slnka ohrievaju zemske jadro. A ako geomaticke burky stlacenim magnetosfery a ionosfery ovplyvnuju pocasie a rast/pokles teplot.
Re: Re: oteplování
Stanislav Florian,2016-11-21 12:35:59
Průměrný tepelný tok z nitra Země je o několik řádů nižší (udává se v mW·m-2 asi 87 mW/m2) než je tepelný tok od Slunce ( asi 165 W/m2 na povrch Země ).
http://is.muni.cz/el/1431/podzim2011/G1101/9009799/prednaska-termika2011.txt?lang=cs
http://aaronsenvironmental.com/wp-content/uploads/2012/11/stephens-earth-energy-balance-diag-crop-600.gif
Největší oteplení je v Arktidě, protože % podíl CO2 na skleníkovém jevu je tam vyšší ( až 26% skleníkového jevu) vzhledem k malé mu množství vodních par ve studeném vzduchu. A roste ppm CO2.
Píšete :"no pretoze teplota nezavisi na CO2, ale CO2 zavisi na teplote."
Kde je k tomu nějaký vědecký důkaz? Nárůst teploty závisí na pohlcování IR záření a lze to prokázat měřením spekter, to není dojmologie, ale fyzikální jev.
Re: Re: Re: oteplování
Petr Kr,2016-11-21 16:03:03
A možná druhý fyzikální jev je to:
teplota nezavisi na CO2, ale CO2 zavisi na teplote
Jestliže v létě je tepleji, než na jaře, proč bylo 5. a 6. května o více než 10°C tepleji než 20 dnů v létě a tepleji o více než 60 letních dnů? No protože je tu několik efektů a teplotu ovlivňuje nejen délka dne, ale i proudění vzduchu. Ten za Sahary nás asi ohřívá.
Teď už jen, který ten fyzikální jev vítězí a který je sice jednoznačný v laboratoři, ale v praxi?
Nevím sám.
Re: Re: Re: oteplování
Michal Lichvár,2016-11-24 10:59:54
Píšete :"no pretoze teplota nezavisi na CO2, ale CO2 zavisi na teplote."
Kde je k tomu nějaký vědecký důkaz?
... nepisal ste aj vy niekde vyssie, ze zo stupajucou teplotou sa uvolnuje viac CO2 z oceanu do atmosfery.
Ja napadam tu spatnu vazbu. Niekdo tu v komentari spomenul, ze vlastne neexistuje vedecka studia, ktora by podporovala tvrdenie, ze s narastom koncentracie CO2 narasta aj sklenikovy efekt. Je to len teoria.
Re: Re: Re: oteplování
Radoslav Porizek,2016-11-24 22:05:16
"Největší oteplení je v Arktidě, protože % podíl CO2 na skleníkovém jevu je tam vyšší ( až 26% skleníkového jevu)... "
Hmm, a na Antarktide je to ako? Tam je situacia uplne opacna, pretoze sa jedna o uplne opacny pol ?
;)
Re: Re: Re: Re: oteplování
Stanislav Florian,2016-11-28 22:22:03
Antarktida je pevnina s trvalým sněhovým pokryvem a stálým albedem, malou výměnou vzduchu po velkou část zimy. Pobřežní ledy Antarktidy významně tají a je z teplejšího moře více srážek ( tok ledovců po svazích do moře atd.), tím se uvolní hodně sladké vody, která zůstane na povrchu a snáze zmrzne. Plovoucí led Antarktidy se tím zvětšuje, zvyšuje se albedo ( led proti oceánu) a tím se ochlazuje, čili zpětná vazba, která teploty stabilizuje. A bylo to tak dlouhodobě, Grónský ledovec má ve vrtu přes 60 lokálních výkyvů teploty, vrt Vostok mnohem méně.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce