Už jsme si zvykli, že svět kvantové mechaniky vyznává podivné zákonitosti, které se vzpěčují naší zkušenosti. A zároveň se utěšujeme tím, že se tyhle kvantové podivnosti omezují na velmi nepatrné objekty a škály. Jenže, nejspíš bychom si tím neměli být až tak úplně jistí.
Vyloženě klasickou kvantovou podivností je superpozice. Jednoduše řečeno jde o to, že objekty mohou existovat ve více různých stavech zároveň. Zní to zvláštně, ale taková je prostě kvantová mechanika. Například, podle tohoto principu elektrony mohou rotovat po směru hodinových ručiček i proti jejich směru zároveň. Anebo mohou být zároveň neexcitované a excitované.
Se superpozicí se ostatně potýkal už před dlouhými desítkami let Erwin Schrödinger, který vymyslel svou slavnou Schrödingerovu kočku jako zlomyslný myšlenkový pokus vysmívající se právě kvantové superpozici. Jenže se to zvrtlo, Schrödingerova kočka začala žít vlastním životem, proslavila kvantovou mechaniku po celém světě, a superpozici se už dneska nikdo nevysmívá. Fyzici prokázali, že částice doopravdy mohou být ve stavu superpozice, a že náš svět je skutečně hodně divné místo. Otázkou ovšem je, kde se to zastaví.
Fyzici MIT teď přicházejí s tím, že kvantové efekty nejsou omezené jenom na neviditelné vzdálenosti. Podle nich totiž neutrina, elementární částice s velice malou hmotností ze skupiny leptonů, mohou být ve stavu superpozice na vzdálenost stovek kilometrů. Jejich výsledky, které se objevují v červencovém čísle časopisu Physical Review Letters, tak prý představují největší vzdálenost na jaké kdy byly testovány kvantové efekty.
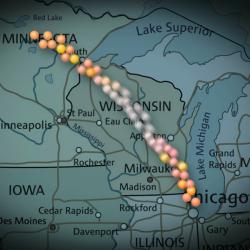
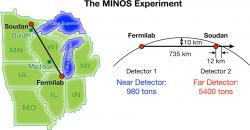
Klíčovou roli v tomto objevu sehrál experiment Fermilabu MINOS (Main Injector Neutrino Oscillation Search). V rámci experimentu jsou v zařízení Fremilabu NuMI, tedy poblíž Chicaga (Illinois) produkována neutrina a pak je posílají do detektoru, který je dole v Soudanu, stát Minnesota, ve vzdálenosti 735 kilometrů. Neutrina se řítí vesmírem rychlostí blízkou rychlosti světla a jenom velmi málo se starají o okolní hmotu. Během svého letu ale podle všeho neutrina oscilují mezi tím, jaký typ neutrina jsou. Když Chicago opouští neutrino určitého typu, tak cestou osciluje a může přiletět do Soudanu jako neutrino jiného typu.
Fyzik David Kaiser a jeho kolegové prostudovali distribuci typů neutrin produkovaných v Chicagu a porovnali ji s distribucí typů neutrin detekovaných v Soudanu. Nakonec dospěli k závěru, že pozorované distribuce neutrin lze nejlépe vysvětlit tak, že neutrina jsou během letu mezi Chicagem a Soudanem ve stavu superpozice a nenabývají podobu jednoho konkrétního typu.
Podle Kaisera je naprosto fascinující, že kvantové mechanice neutečeme, ani když se pohybujeme na pořádně velkých vzdálenostech. Jak se zdá, kvantově mechanický popis se nám hodí, i když v USA překračujeme hranice jednotlivých států. Oproti očekávání se kvantová mechanika nebojí makroskopických měřítek.
Video: How the Hippies Saved Physics — David Kaiser
Literatura
MIT 19. 7. 2016, Wikipedia (Neutrino)
Oscilace neutrin – cesta k nové fyzice
Autor: Vladimír Wagner (21.04.2010)
500 mílový neutrinový experiment Fermilabu odstartoval
Autor: Stanislav Mihulka (07.10.2014)
Extrémní neutrino poprvé vystopováno mimo Mléčnou dráhu
Autor: Stanislav Mihulka (25.04.2016)
Diskuze:
Signál mimozemšťanů
Viliam Mlich,2016-07-25 14:51:48
Možná právě superpozice jsou tím signálem mimozemšťanů, a ne náhlé zhasnutí hvězdy.
Upřesnění
Pavel Brož,2016-07-21 23:18:58
Bohužel ze článku není patrno, co vlastně bylo tím podstatným novým příspěvkem k experimentální neutrinové fyzice, potažmo obecně k experimentálnímu testování kvantové teorie. Není to chyba autora Stanislava Mihulky, zavádějící formulace jsou totiž obsaženy už ve zdrojovém článku, z nějž zřejmě čerpal (předpokládám, že jde o zdroj http://news.mit.edu/2016/neutrinos-weird-quantum-effects-over-hundreds-miles-0719).
Asi bude nejlepší začít krátkým resumé toho, co NENÍ tím podstatným v referovaném experimentu, následně pak rekapitulací některých klíčových pojmů z kvantové teorie, a finálně pak bude srozumitelnější, o co zde šlo.
Takže co NENÍ podstatné, ačkoliv by se to mohlo zdát:
a) není podstatná (ani výjimečná) velikost pozorovaného stavu kvantové superpozice,
b) experiment nemá žádný vztah k problematice superpozic makroskopických těles, známých jako paradox Schrödingerovy kočky,
c) v experimentu nefiguruje kvantové provázání (entanglement) – toto sice není ve článku zmíněno, nicméně v diskuzi se to objevilo, takže preventivně zmiňuji, že o entanglement zde vůbec nejde, plus navíc je to důležité v pozdějším výkladu,
d) hlavním přínosem experimentu není pozorování oscilace neutrin, ale nová realizace experimentu, ve kterém se na základě narušení specifických nerovností vylučuje celá kategorie „klasických“ alternativ ke kvantové teorii.
Co se týče velikosti pozorovaného stavu kvantové superpozice – název článku (dokonce už názvu originálního zdroje) by mohl sugerovat, že byl pozorován kvantový stav neutrin o velikosti cca 735 km. Není tomu tak. Kvantový stav neutrin měl ve skutečnosti mikroskopický rozměr, jednalo se pouze o to, že coby kvantový stav „vydržel“ až na vzdálenost 735 km, která dělila detektor od zdroje neutrin. Neutrina tuto vzdálenost urazila za necelé 2,5 milisekundy, což v kvantovém světě není nijak krátká doba, ale není ani nijak rekordně dlouhá. Vlastně můžeme říct, že experiment potvrdil, že paprsek neutrin zůstal koherentní i po uražení vzdálenosti 735 km, tzn. že během této cesty nedošlo k dekoherenci jejich kvantového stavu. Samotná „velikost“ tohoto kvantového stavu byla ve skutečnosti dána pouze rozbíhavostí neutrinového svazku, a ta je zase ovlivněná parametry generujícího svazku částic, jejichž srážkami neutrina vznikala. Tzn. velikost toho stavu byla v okamžiku zrodu neutrin subatomárně malá, a dále se zvětšovala pouze v důsledku divergence paprsku – ve výsledku byla každopádně řádově menší než zmíněné stovky kilometrů.
Zmínky o Schrödingerově kočce se bohužel staly jakousi povinnou mantrou většiny popularizačních článků, ve kterých se objevuje superpozice. Superpozice sama o sobě přitom není nic výjimečného ani nového – za jejího objevitele může být považován už Christiaan Huygens, viz Huygensův princip (např. zde https://cs.wikipedia.org/wiki/Huygens%C5%AFv_princip). Superpozice je přirozenou součástí jakéhokoliv vlnění, u kterého lze zanedbat nelineární efekty – může jít o každému dobře známé vlnění hladin kapalin, nebo o akustické vlnění ať už ve vzduchu, nebo v kapalných či pevných látkách, superpozice byla od začátku velice dobře rozpoznána také v teorii elektromagnetického pole, speciálně pak v jeho části týkající se elektromagnetických (tedy i světelných) vln, a v každé klasické teorii pole v lineárním přiblížení figuruje taktéž. Schrödingerova kočka je paradoxem proto, že se v ní superponuje makroskopický stav, u kterého se superpozice naprosto nepředpokládá – nečiní žádný problém představit si superpozici dvou vln na hladině rybníka, ovšem představit si superpozici živé a mrtvé kočky už problém činí. Přibližovat superpozici zrovna na příkladu Schrödingerovy kočky je tudíž podobné, jako přibližovat sčítání a odčítání na příkladu trojných integrálů. Jako stavy Schrödingerovy kočky se nazývají superpozice makroskopických vázaných stavů mnoha částic – např. krystal či jakékoliv těleso v pevném či kapalném skupenství je vázaným stavem částic, z nichž se skládá, naopak plyn není vázaným stavem molekul. Ani paprsky částic v urychlovačích netvoří vázaný stav, a tudíž ani u nich se o stavech Schrödingerovy kočky nedá mluvit. Částice v paprsku ve skutečnosti tvoří soubor na sobě nezávisle se chovajících entit, a jejich stavy jsou popisovány pomocí jednočásticových vlnových funkcí, což lze bez jakékoliv újmy provést vždy, když interakci mezi jednotlivými částicemi v tomtéž paprsku můžeme zanedbat (což v urychlovačích vždycky můžeme).
Ze stejného důvodu v referovaném experimentu nehraje žádnou roli kvantová provázanost (entanglement). Ten hraje roli u speciálně připravených dvojic částic, zatímco v daném experimentu každé z neutrin vznikalo „jednotlivě“. Těch neutrin sice bylo generováno obrovské množství, ale žádná provázanost mezi nimi nebyla.
Oscilace neutrin hrají v experimentu sice důležitou, ale spíše pomocnou roli, protože hlavním přínosem experimentu je nová realizace pokusu, ve kterém se potvrzuje narušení tzv. Leggett-Gargových nerovností. A právě nyní to začne být konečně zajímavé, protože právě o testování těchto nerovností šlo v tomto experimentu především.
S kvantovou teorií se pojí vícero nerovností, jako jsou např. tzv. Bellovy nerovnosti, potom také Clauser-Horne-Shimony-Holtovy (CHSH) nerovnosti, dále Leggettovy nerovnosti, potom také Leggett-Gargovy nerovnosti, a tím jejich výčet zdaleka nekončí. Všechny mají jedno společné – jejich platnost je vyžadována celými kategoriemi teorií, které splňují několik obecně formulovaných axiomů. Tak např. Bellovy a CHSH nerovnosti musí být splněny ve všech teoriích, které splňují axiomy lokality a realismu. Pokud experiment ukáže, že jsou tyto nerovnosti narušeny, tak z toho automaticky plyne, že skutečnost nemůže být adekvátně popsána žádnou teorií z dané kategorie. To je diametrální rozdíl oproti běžnému experimentálnímu testu – běžný test totiž pouze dá odpověď na otázku, zda některé uvažované teorie jsou či nejsou v souladu s výsledkem experimentu. Oproti tomu spolehlivé experimentální ověření, že Bellovy nerovnosti jsou narušeny, automaticky falzifikuje VŠECHNY teorie, které stojí na předpokladu lokálního realismu. Kvantová teorie mimochodem nesplňuje především předpoklad realismu (ten je samozřejmě matematicky precizně formulován).
Bellovy nerovnosti byly vůbec prvním takovým příkladem „kategoriálního“ testu, který měl tu sílu vylučovat celé obecné skupiny teorií. Po Johnu Bellovi přišli další, kteří jeho myšlenku rozvíjeli, a kteří vymysleli vlastní varianty nerovností. Už zmíněné Bellovy a CHSH nerovnosti jsou prubířským kamenem všech lokálních a současně realistických teorií. Oproti tomu Leggettovy a Leggett-Gargovy nerovnosti se koukají na zoubek celé kategorii všech nelokálních a současně realistických teorií. Hlavní rozdíl je mezi nimi v tom, že Bellovy, CHSH a Leggettovy nerovnosti jsou aplikovatelné pouze na specifické experimenty prováděné na entanglovaných částicích, oproti tomu Leggett-Gargovy nerovnosti jsou aplikovatelné na jiné specifické experimenty, které už entanglement nevyžadují (a právě proto mohou být použity v souvislosti s neutrinovým experimentem, ve kterém entanglement vůbec nefiguruje). Klíčovou podmínkou pro použitelnost Leggett-Gargových rovnic ale je, aby testovaný systém byl ve stavu kvantové superpozice. A nyní se už konečně blížíme k rozlousknutí podstaty celého referovaného experimentu.
Experimentátoři si totiž umínili, že právě tento kruciální test Leggett-Gargových nerovnic zrealizují s pomocí neutrinového svazku. Proč právě neutrinového? Inu protože velice dobře prochází hmotou, díky čemuž není dnes žádným problémem detekovat neutrina stovky kilometrů od zdroje. No a proč nedetekovali místo neutrin třeba fotony, které bez problémů umí překonat kosmologické vzdálenosti mezi místem jejich zrodu a místem jejich detekce? Zde hrálo asi určitě roli jednak to, že s fotony je to nuda, na nich už dávno jejich kvantové vlastnosti ověřil kde kdo. A jednak se jednalo o to, že neutrina mohou být také v superpozicích (což ale u světla funguje taky, není problém vytvořit superpozici dvou různých polarizačních stavů světla), plus ale navíc se tato superpozice díky jejich oscilacím vyvíjí v čase. A právě to umožňuje zapojení Leggett-Gargových nerovností, protože ty jsou postaveny na korelacích výsledků měření v různých časech (blíže viz např. zde https://en.wikipedia.org/wiki/Leggett%E2%80%93Garg_inequality).
Laskavý čtenář nechť si nyní přidrží klobouk, konečně začínáme při jízdě s kopce nabírat tu správnou rychlost. Neutrina se rodí v závislosti na typu reakce buďto jako elektronová, nebo jako mionová, nebo jako taunová. Mohli bychom použít analogii se světlem, kdy např. po totálním odrazu od nějaké plochy „vznikne“ foton s lineární polarizací ve směru roviny té plochy. Pokud plochu natočíme kolmo k předešlému stavu, získáme foton s polarizací kolmou k té, kterou získal foton v předchozím natočení. Stav každého takového fotonu ale můžeme vyjádřit jako superpozici stavu, který by měl kdybychom plochu nastavili postupně dvakrát různě a šikmo k obou předchozím nastavením.
S neutriny je to (vzdáleně) podobné – ať už generujeme elektronová, anebo mionová, anebo tauonová neutrina, každé z nich je v superpozici tří bázových stavů, které jsou význačné tím, že každý z nich má nějakou odpovídající hmotnost. V té význačnosti bázových stavů je mimochodem zásadní rozdíl mezi těmi neutriny a fotony, obě polarizace fotonů totiž mají tutéž – nulovou – hmotnost, a proto jakákoliv jejich superpozice může sloužit za stejně dobrý bázový stav jako jakákoliv jiná superpozice, žádná báze u fotonů tedy není význačná. Tři bázové stavy neutrin, každé odpovídající přesně definované hmotnosti, se typicky označují ný_1, ný_2, ný_3, zatímco jejich superpozice odpovídající elektronovému, mionovému či tauonovému neutrinu se označují ný_e, ný_mí, ný_tau. Tak např. ný_e se rovná jedné konkrétní superpozici ný_1, ný_2, ný_3, zatímco ný_mí a ný_tau se rovnají jiným superpozicím.
Různost hmot bázových stavů ný_1, ný_2, ný_3 je klíčová, protože každému z nich odpovídá de Broglieova vlna, jejíž vlnová délka závisí právě na velikosti příslušné hmotnosti. Tzn. že vlnové délky se pro každý bázový stav liší. A když skládáme tři vlny, každou o jiné vlnové délce, tak získáme velice estetické oscilační vzory. Tak např. na tomto obrázku je zobrazeno, jak se ty vlny vyvíjí, pokud na začátku máme elektronové neutrino (čili takovou kombinaci bázových stavů ný_1, ný_2, ný_3, které odpovídá ný_e):
https://en.wikipedia.org/wiki/File:Oscillations_electron_long.svg
Tento vzor zase získáme, pokud na začátko bylo mionové neutrino:
https://en.wikipedia.org/wiki/File:Oscillations_muon_long.svg
a tento když začneme s tauonovým neutrinem:
https://en.wikipedia.org/wiki/File:Oscillations_tau_long.svg
Tyto oscilace byly už ověřeny pro všechny typy neutrin, v čem je tedy referovaný experiment nový? Právě zapojením těch nerovností. To, že neutrina oscilují je jedna věc, nicméně hypoteticky bychom si mohli představit nějaký mechanismus jejich periodické změny, něco úplně mimo kvantovou teorii. Oscilace neutrin ale umožňují také počítat specifické korelace, které figurují v Leggett-Gargových nerovnostech – umožňují to právě proto, že ten kvantový stav se vyvíjí, v různých místech detekce tedy získáváme různé superpozice, a jejich korelace pak můžeme počítat. To je rozdíl od třeba fotonového paprsku šířícího se ve vakuu, ten se totiž (co se týče jeho superpozice) nevyvíjí, zůstává stejný. To samozřejmě neznamená, že by se pro něj nedal vymyslet nějaký experiment, kde by se Leggett-Gargovy nerovnosti nedaly zaměstnat, ale musely by se tam vnést nějaké prvky, které ten stav mění.
Abych byl přesný, zbývá dodat ještě jeden detail – v tom referovaném experimentu nebyly použity přesné Leggett-Gargovy nerovnosti, ale jejich zobecnění odvozené jistým J.A.Formaggiem. Všímavý čtenář si totiž na příslušných wikipedických stránkách mohl povšimnout, že pro Leggett-Gargovy nerovnosti je zapotřebí, aby detekce byly nejméně tři, ve třech různých časech, potažmo ve třech různých místech neutrinového paprsku. V experimentu byla ale detekční místa pouze dvě, na začátku paprsku a potom v cílovém místě. Proto Formaggio vymyslel upravenou variantu zmíněných nerovností, které kompenzují chybějící měření zahrnutím korelací pro různé energie neutrin. A právě zde se dostáváme mimochodem i k tomu, čím zásadním se experiment MINOS liší od jiných oscilačních experimentů, jak už zde zmínil Vladimír Wagner, a to konkrétně možností přesného měření energie neutrin.
Tím se kruh uzavřel, děkuji váženému čtenáři za trpělivost :-)
Gran Sasso
Jakub Preclík,2016-07-20 10:07:01
Z CERN do Fran Sasso je to 730 Km a oscilace neutrin tam byla prokazana experimentem OPERA take a uz je to par let. Jedine v cem me napada ze byl experiment MINOS dokonalejsi, ze umel detekovat neutrina ve vsech trech stavech. Gran Sasso umel tusim jen elektronova a mionova. Ale v clanku to chybi. Kdyby prosim autor mrkl do zdroju a podival se na jaka neutrina byl citlivy detektor MINOS experimentu.
Re: Gran Sasso
Vladimír Wagner,2016-07-20 18:44:01
Tady musím udělat opravit. Detektor OPERA byl zaměřený na identifikaci tauonových neutrin. Proto využíval velmi speciální techniku (Pro podrobnosti starší článek zde: http://www.osel.cz/5073-prvni-prime-pozorovani-oscilace-mionoveho-neutrina-na-tauonove.html , jen pro doplnění se v následujících letech podařilo detekovat několik málo dalších tauonových neutrin. Výsledek plně odpovídal předpovědi. Naopak u detektoru MINOS je možnost určit i elektronová neutrina, ale jeho hlavní výhodou je poměrně přesné měření energie neutrina a odlišení mionového neutrina a antineutrina. Taková zkoumání by měla umožnit pozorování rozdílu mezi hmotou a antihmotou v tomto sektoru a nakonec také umožnit zjistit, jaké je pořadí hmotnosti neutrin. Trochu o těchto zkoumáních je zde http://www.osel.cz/6216-opet-neutrina-jedno-potvrzeni-a-jedno-popreni.html v části: Studia oscilací mionových neutrin a antineutrin z urychlovačů.
Moc to
Mojmir Kosco,2016-07-20 06:55:50
Nechapu jsou ta neutrina svazana pred vypustenim pri vypusteni nebo pri zachytu ?
Re: Moc to
Jakub Preclík,2016-07-20 10:15:35
Nejsou provazana. Jsou v superpozici enegetickych stavu. Celkem jsou to 3 stavy kterym se rika neutrino elektronove, mionove a tauonove. Elektronove je nejlehci a tauonove je nejtezsi. Je to pekna podivnost, ale vyplyva to z teorie a experimenty to potvrdily do urcite urovne uz nejaky rok. Napriklad neutrina chytana ze slunce. Byl to tehdy pekny sok, kdyz chytali jen tretinu predpovezeneho toku. Nakonec se zjistilo, ze detektor umel chytat jen neutrina jednoho typu a ty zbyle dva typy nevidel. Jedna z krasnych shod teorie a jejich podivnosti s fyzikalnim experimentem.
Nase mysl nema sanci takovou vec pojmout intuitivne. Proto je kolem kvantove fyziky porad tolik dojmologickych a emocnich zmatku.
Re: Re: Moc to
Vladimír Wagner,2016-07-20 18:53:21
Musím Vás trochu poopravit. S tou hmotností to je trochu komplikovanější. Elektronový stav, mionový stav a tauonový stav neutrina nemají přesně definovanou hmotnost a jsou různými směsmi tří jiných stavů, které mají přesně definovanou hmotnost. Jaké je pořadí hmotnosti se přesně neví (co měříme je rozdíl hmotností). Existují dvě možnosti a právě experimenty na svazku z Fermilabu by mohly rozhodnout, která je správná.
Neutrina
Vlastislav Výprachtický,2016-07-20 06:12:54
Projev oscilace neutrin znamená, že neutrino s nenulovou hmotností se může přeměnit na neutrino s hmotností nulovou. Podstata přeměny musí být energeticky podmíněna, interakcí to však nebude. V opačném případě se interakcí asi změna projeví.
Re: Neutrina
Jakub Preclík,2016-07-20 10:31:44
Teorie predpovida, ze pokud neutrina maji nulovou hmotnost, oscilovat nesmi. Pokud maji nejakou tak oscilovat musi. Ze maji nenulovou hmotnost uz je experimentalne overeno. Bohuzel se nevi jakou. Jsou znamy jen rozdily mezi temi 3 stavy ktere neutrina maji. Pri zrodu ma neutrino stav dany energii udalosti jeho vzniku. A na kratkou vzdalenost bylo skutecne mereno ze jeho stav energie neosciluje. Po nejake, zatim se nevi zhruba jake, delsi dobe existence neutrina se toto vykasle na svuj puvod a zacne si mit vsechny tri energeticke (hmotnostni) stavy naraz. Pri interakci/dopadu se pak vybere jeden z nich jako znamy kolaps vlnove funkce te superpozice. Takze ano projevi se to az pri interakci.
neutrina oscilují a co jiné částice?
Stanislav Florian,2016-07-19 21:56:21
Neutrina oscilují
http://hp.ujf.cas.cz/~wagner/popclan/neutrina/oscilace.htm
a projevila se kupodivu oscilací.
Naším tělem projde myslím jedno neutrino za vteřinu a nic se neděje. A najednou máme jedno neutrino, které se nechalo chytit dvakrát a to 750 km od sebe.
Nerozumím tomu, vyčkám, o na to V. Wagner.
Re: neutrina oscilují a co jiné částice?
Vladimír Wagner,2016-07-19 23:51:08
Nevím přesně, jestli jsem pochopil dotaz, ale pokusím se odpovědět. Pro začátek jednu opravu. Na cm2 našeho těla dopadá za sekundu 100 miliard neutrin ze Slunce. Přesto zachytíme za život zhruba jen jedno.
Takže teď k tomu dotazu. U experimentu, který je popisován je několik rozdílů oproti neutrinům ze Slunce a lidském tělu jako detektoru. Jde o neutrina produkovaná urychlovačem a s mnohem vyšší energií než ta ze Slunce. Detektor je udělán tak, že je vyladěn na jejich detekci. I tak z mnoha miliard miliard zachytí jen pár. Neutrino detekci nepřežije, takže nemůže být detekováno dvakrát. A kdyby přežilo, tak strašlivě malá pravděpodobnost detekce zabraňuje mít takovou koincidenci. To, co se pozorovalo, bylo, že distribuce různých typů neutrin v blízkém detektoru (detekovala se nějaká neutrina z daného svazku) byla porovnávána s distribucí typů neutrin ve vzdáleném detektoru (detekovala se jiná neutrina ze stejného svazku). Tedy nikdy nešlo o detekování jednoho neutrina dvakrát. Jinak oscilace neutrin jsou čistě kvantový jev a dost těžko můžou být popsána jinak než vlnovou funkcí, která je superpozicí více stavů.
Re: Re: neutrina oscilují a co jiné částice?
Petr Petr,2016-07-20 07:52:49
To jsou jen povídačky. Těžko mohou být popsána jinak, když se to nechce.
(Máte snad matematický důkaz, že to jinak popsat nejde? Jinak se zdržte takových výroků.)
https://en.wikipedia.org/wiki/Neutrino_oscillation#Classical_analogue_of_neutrino_oscillation
Jde jen o to, že jde o "metastabilní stav" s dlouhou periodou, takže i při pohybu rychlostí světla urazí objekt kilometry. Proto to není již mikroskopické, kdy doby pod nanosekundy to omezují na laboratoř.
(Nepletl bych do toho provázanost...)
Re: Re: Re: neutrina oscilují a co jiné částice?
Vladimír Wagner,2016-07-20 19:01:16
Fyzika a matematické důkazy jsou velmi odlišné věci. Můžete mít velice pěkný a konzistentní matematický popis světa, ale jen ten, který odpovídá experimentálním fyzikálním výsledkům je popisem také fyzikálním. Jinak analogie je analogie a nic více (matematické rovnice vyjdou stejné pro řadu velice různých fyzikálních dějů).
Re: Re: neutrina oscilují a co jiné částice?
Kamil Kubů,2016-07-20 07:55:16
Děkuji. Velice jednoduché a srozumitelné vysvětlení.
Jako obvykle u článků o QM je nadpis článku v příkrém rozporu s tím, co bylo podstatou experimentu a jeho výsledným závěrem. Tento nešvar je bohužel vlastností naprosté většiny popularizačních textů o QM, neřkuli i těch skutečně odborných. Možná by stálo za to, aby součástí studia QM byla i lingvistická logika, aby si páni vědátoři uvědomili, jakým způsobme o předmětu svého zájmu poučují okolní svět.
Re: Re: neutrina oscilují a co jiné částice?
Stanislav Florian,2016-07-20 12:50:21
Děkuji panu Wagnerovi.
Jde tedy o svazky neutrin, které se během letu kvantově mění, čímž se mění jejich statistiké složení. Svazek obrovského počtu neutrin, pár jich bylo detekováno v jednom detektoru a pár z téhož svazku v druhém 735 km daleko.
" distribuce neutrin lze nejlépe vysvětlit tak, že neutrina jsou během letu mezi Chicagem a Soudanem ve stavu superpozice a nenabývají podobu jednoho konkrétního typu. "
Během letu se tedy mohou měnit oscilací na některou ze tří možností.
Kantové provázání
https://cs.wikipedia.org/wiki/Kvantov%C3%A9_prov%C3%A1z%C3%A1n%C3%AD
"Pokud je později částice A naměřena ve stavu 1, znamená to, že vlnová funkce zkolabovala do levé větve a částice B je ve stavu 2.
Měření jedné z částic okamžitě mění stav její entanglované partnerky."
Zdá se, že kvantové provázání se týká jedné samotné částice. A že kvantová vlastnost se mění samotným měřením. Cesta ke kvantově provázaným počítačům asi daleká.
Vesmír
Milan Krnic,2016-07-19 20:41:31
Z naší, tedy alespoň z mojí zkušennosti je vše proměnlivé.
Trochu navazující ... ani nevíme, zda ve Vesmíru existují dva shodné objekty.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce