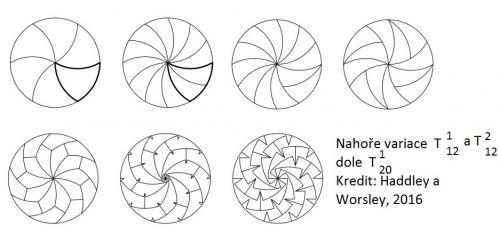
Matematici jsou zvláštní tvorové a jak říkával Pan Horníček, hloubají nad věcmi, které jsou ze své podstaty, zcela neupotřebitelné. Maří čas i nad tím o čemž předem ví, že i když to vyřeší, nebude to k ničemu. Někdy se naštěstí mýlí. Joel Haddley a Stephen Worsley z Katedry matematických věd, University of Liverpool se v poslední době věnovali  „kuchařovu dilema“. Výsledkem je recept na uspokojení  zákazníka, který nechce střed koláče, případně nechce jeho okraj. Přitom to lze zaonačit tak, že se nikdo necítí být ošizen. Všichni  dostanou stejně velký kus a porce nejen, že mají stejnou plochu, ale i tvar. Ten je navíc tak trochu uměleckým dílem.

 

 

Z obrázku na konci článku je vidět, jak je řešení takové úlohy jednoduché a že bychom na to přišli sami také. Pokud by nás ovšem taková blbost napadla a naše abstraktní myšlení by zvládlo zadat to do patřičných vzorců dlaždicového dělení kruhové plochy. Postižení jedinci vnímající svět čísly, o novém řešení nyní na fórech hodně diskutují, používají při tom termín monohedral tilings. Hezky česky asi „parketování“. Odbornější hantýrkou se členění plochy na opakující se vzory přezdívá ještě méně libozvučnějším termínem - teselace. Ještě větší nadšenci než je zmíněné duo Angličanů,  vztáhli teselaci z plochy  i na členění prostoru, což už je zcela mimo zdravý rozum i schopnosti autora tohoto článku.

 

 

Příroda se k teselacím také občas uchyluje. Například když rostoucí krystaly vyplňují nějaký předem daný prostor. Nějak intuitivně to zvládají i včely když staví voskové komůrky svým ratolestem. Matematici to bez vzorců a počítání nedovedou, ale i tak se mozaikářům a módním návrhářům vyplatí s nimi být zadobře. Dovedou jim ušetřit  výrobní náklady. Jednak jednoduchou teselací (s pravidelnými mnohoúhelníky stejného tvaru), nebo složitější, zvanou polopravidelnou (s pravidelnými mnohoúhelníky více než jednoho tvaru).

 

 

Teselací už se dnes neřeší jen dlažba v koupelně, ale i nos raketoplánu. My běžní smrtelníci se s ní ale nejčastěji potkáváme u věcí zcela nepraktických, hlavně v kumštu. Tam k jejímu rozmachu přispěl anikonismus, což je v podstatě ptákovina zakazující zobrazování živých tvorů. Objevila se vznikem monoteismu. Svědčí o tom i desatero, které  Hospodin předává na hoře Sinaj Mojžíšovi, a které začíná slovy: "Já jsem Hospodin, tvůj Bůh; já jsem tě vyvedl z egyptské země, z domu otroctví. Nebudeš mít jiného Boha mimo mne. Nezobrazíš si Boha zpodobením ničeho, co je nahoře na nebi, dole na zemi nebo ve vodách pod zemí. Nebudeš se ničemu takovému klanět ani tomu sloužit." (Exodus 20, 2-5).

 

 

Umění se s náboženskou cenzurou snažilo popasovat a jak se mu to dařilo je patrné na biblickém příběhu ztvárněném v židovské hagadě. Story vycházející z judaismu, často považované za základ mnoha jiných monoteistických náboženství, včetně křesťanství a islámu, se malíř snažil podat co nejlépe uměl, ale tak aby se při tom nedostal do maléru.

Výsledkem je, že nás ztvárnil s něčím ještě horším, než když nám Darwin nasadil opičí hlavu. Konzervativní islám si anikonismus podržel dodnes a za zveřejnění proroka Mohameda jsou jeho stoupenci ochotni i vraždit. Tou lepší stránkou anikonismu je, že se dnes můžeme kochat nádherou paláce Alhambra mauzolea Tádž Mahal,…

 

 

Ani v 21. století ale není teselace mrtvým uměleckým směrem. Doznala jen změn v nichž ji už nepoznáváme. Výraznou světovou osobností, která ji vdechla nový rozměr, je nizozemský výtvarník Mauritse Cornelise Eschera. Ukázky z jeho díla zde.

 

 

Z matematického pohledu je prý uměleckým dílem i to, čím nyní Angličané rozšířili dosud známé hvězdicové porcování pizzy. Nové variace teselace svým hostům ale budou prý moci nabídnout jen ty nejvybranější pizzerie a až po dovybavení novými modely chirurgického laser-nože.

 

 

 

Teselace obdivuhodně zvládali i starověcí umělci: Secret of Taj Mahal

Alhambra



Literatura

Infinite families of monohedral disk tilings, arXiv:1512.03794