Nedávno jsem přednášel studentům na FJFI ČVUT o produkci supertěžkých prvků a rozebíral i novinky a výhledy v tomto oboru. V populárnější formě je povídání o této oblasti výzkumu v nahrávané přednášce v rámci Týdne vědy a techniky. Také jsem se zmínil, že čekám v nejbližší době uznání supertěžkého prvku s protonovým číslem 113. Některé jeho izotopy byly poprvé produkovány pomocí tzv. horké fúze v laboratoři SÚJV Dubna a izotop s jiným počtem neutronů se pomocí tzv. studené fúze podařilo vyprodukovat japonským fyzikům v laboratoři RIKEN. Podrobnější popis rozdílu mezi studenou a horkou fúzí je zde. Prvek 113 je nejtěžším, který se pomocí studené fúze nejspíše dá vytvořit. Supertěžké prvky se rozpadají buď rozpadem alfa nebo spontánním štěpením. Po jeho vzniku tak dostáváme kaskádu rozpadů alfa, která končí buď u izotopu transuranu s delší dobou života nebo právě samovolným štěpením. A právě pomocí detekce rozpadů a hlavně alfa částic, které při nich vyletují, se supertěžké prvky identifikují. Ty ze studené fúze mají konec kaskády rozpadů v oblasti známých izotopů, ty z horké fúze končí svou kaskádu u izotopů, které nebyly známé. Nebylo tak jisté, zda je jejich identifikace správná. V Dubně tedy vytvořili daný prvek první, ale Japonci přidali ten neprůstřelný důkaz, že jej opravdu máme a pomohli i fyzikům v Dubně s potvrzením jejich výsledků. Navíc je tento supertěžký prvek první, který měl šanci být pojmenován v Japonsku a obecně v Asii. Uvažoval jsem, jak tuto situaci Mezinárodní unie pro čistou a užitou chemii (IUPAC) vyřeší, aby se skupina z Dubny necítila poškozená přiklepnutím objevu laboratoři RIKEN. Pro připomenutí lze uvést, že naposledy byly uznány v roce 2011 dva prvky s protonovými čísly 114 a 116, které dostaly nakonec jméno flerovium a livermorium (podrobněji zde). A předtím v roce 2010 pak prvek s počtem protonů 112, který dostal název kopernicium (podrobněji zde).
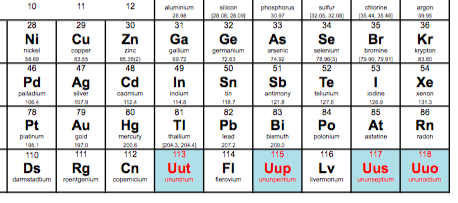
Část periodické tabulky s novými uznanými supertěžkými prvky (stránka IUPAC).
A řešení se našlo geniální. Na jeden zátah schválily komise IUPAC hned čtyři supertěžké prvky. Laboratoř v Dubně spolu s kolegy z Livermoru tak mohou oslavovat hned tři prvky a rádi tak japonským kolegům pogratulují. Je třeba uznat, že v současné době jsou všechny velice dobře potvrzeny společným úsilím několika laboratoří, kromě již zmíněných je třeba určitě vzpomenout laboratoř GSI Darmstadt. Navíc je nyní období, kdy pravděpodobně potrvá delší dobu, než se další supertěžký prvek vyprodukuje a jeho existence potvrdí. Bude to nejspíše ten s protonovým číslem 120. V jádře totiž působí párování mezi nukleony a sudý počet protonů přispívá k vyšší stabilitě jádra. Problém je, že se nyní s růstem protonového čísla začínáme vzdalovat od ostrova stability a tím je vyprodukovaný izotop prvku méně stabilní a jeho doba života je kratší, Najít způsob, jak získat správný výsledný poměr počtu protonů a neutronů, abychom produkovali nejen těžší prvky, ale také izotopy supertěžkých prvků, které jsou na ostrově stability a jejich doba života může být i dost dlouhá, bude hodně náročné.
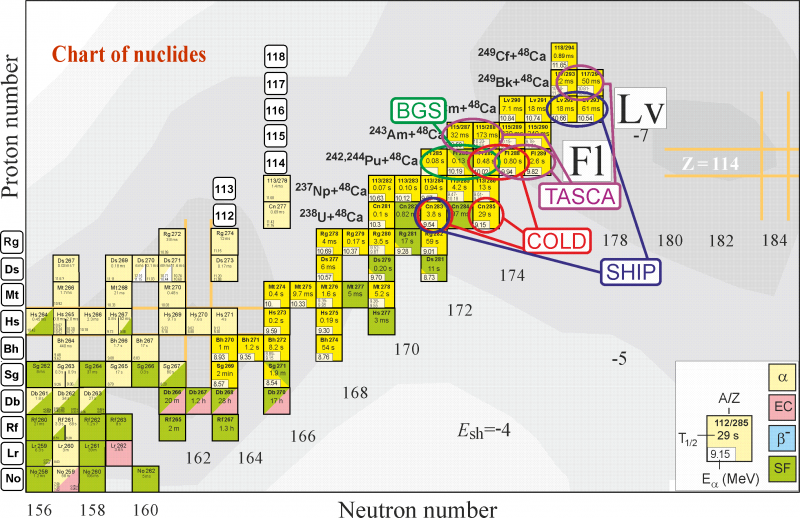
Mapa různých izotopů supertěžkých prvků s vyznačením různých metod a zařízení, které se na jejich objevu podílely. Je vidět, že například izotopů prvku 113 je už známo 6. A úplně nalevo odskočený od ostatních pěti je ten vyprodukovaný ve studené fúzi v Japonsku. Úplně napravo je vyznačen ostrov stability s protonovým magickým číslem 114 a neutronovým 184. (Zdroj prezentace S. Dmitrieva na loňské konferenci ve Varně).
Zatím je velmi zajímavé se věnovat chemii s jednotlivými atomy, při které se daří zkoumat chemické vlastnosti i prvku s protonovým číslem až 112 (kopernicium) a pracuje se i na těch těžších. Velmi zajímavé je, zda i při tak velkém počtu elektronů, které se navíc stávají relativistickým, se zachovává periodicita známá z Mendělejevovy tabulky.
Vzhledem k tomu, že se jedná o velice zajímavé téma a třeba právě v SÚJV Dubna a GSI Darmstadt se připravuje řada nových metod a zařízení, připravuji pro Osla a Technet společný rozsáhlejší článek, který by se zaměřil hlavně na výhledy a možnosti, jak získat nové izotopy známých i nových supertěžkých prvků.
Pojmenování nového supertěžkého prvku na obzoru
Autor: Vladimír Wagner (22.06.2009)
Návrh na pojmenování nového prvku zní kopernicium
Autor: Vladimír Wagner (03.08.2009)
Dorazili jsme k břehům ostrova stability?
Autor: Dagmar Gregorová (29.09.2009)
Uznána existence dalších dvou supertěžkých prvků
Autor: Vladimír Wagner (21.06.2011)
Diskuze:
Novopredpovedané jadrá
Lubomir Vlcek,2017-02-23 15:01:35
http://vixra.org/pdf/1506.0207v1.pdf
Superheavy Spherical Nuclei. Island of Stability
In the present paper we show, that nuclei Os 192, Pt 198, Hg 198, Hg 200, Hg 201, Hg 204, Tl 205, Pb 206, Pb 207, At 210, Pa 231, Th 232, AcU 235, Np 237, Pu 240, Am 242, Cm 247, Ku 261, and more create an island of stability. Keywords: superheavy spherical nuclei, island of stability, sphere 192 PACS number: 21.60.-n
Spheres in nuclei
Journal of Mathematical Modeling and Operations Research, Vol. 1, No. 1
Page 1 – 11.pdf
The New Coordinate Systems in Physics and Magic Numbers
Lubomir Vlcek Rokytov 132, 086 01, Slovak Republic
Email: lubomir.vlcek@gmail.com
Critical examination of fundamentals in physics
http://www.trendsinphysics.info/
academia.edu
https://tuke.academia.edu/LubomirVlcek
L. Vlcek, : New Trends in Physics, Slovak Academic Press, Bratislava 1996,
ISBN 80-85665-64-6.
Presentation on European Phys. Soc. 10th Gen. Conf. – Trends in Physics ( EPS 10) Sevilla ,
E 9. -13 September 1996,
http://www.trendsinphysics.info/
THE NEW COORDINATE SYSTEMS IN PHYSICS AND MAGIC NUMBERS
This paper presents two new coordinate systems (s, t, u, v) and (s*, t*, u*, v*). There is a transformation of relations between (s, t, u, v) and (x, y, z) - cartesian between (s*, t*, u*, v*) and (x, y, z), between (s, t, u, v) and (s*, t*, u*, v*). The theory is an attempt to account for the existence of magic numbers in terms of interactions between an individual nucleon and a force field produced by all the other nucleons. Combination of the cartesian coordinate system with our news coordinates arise as very firmly fastening structure for description of nuclear spheres (shells).
http://www.trendsinphysics.info/kniha/new.html
New Trends in Physics CD Rom /book, Elementes Pictures, Spheres in Nuclei, Forecasted Nuclei...42
67 Pages. New Trends in Physics /book, elementes pictures, spheres in nuclei, forecasted nuclei, ZOO-3D editorfor interactive inspecting of nuclei spheres/, Academic Electronic Press, Bratislava, 2000, CD- ROM, ISBN 80-88880-38-6.
http://www.trendsinphysics.info
JMMOR
ISSN 2377-6404 (online)
................................................................................................................
http://kopecky.rtyne.net/teorie/vlcek.pdf
Malé doplnění
Vladimír Wagner,2016-01-05 16:46:57
Podle nejnovějšího tiskového prohlášení z SÚJV Dubna předpokládají, že jejich návrh pro prvek 115 bude moskovium připomenutí Moskevského regionu, ve kterém se Dubna nachází. Dále vyjádřili určité podivení nad tím, že prvek 113 byl přisouzen Japoncům a ne jim. Jak jsem říkal, je v tomto případě přisouzení s otazníkem.
hranice
Ondrej Musil,2016-01-05 13:05:29
Hezky den, omlouvam se za laicky dotaz, ale existuje nejaka hranice za kterou jiz nebude mozne nove prvky syntetizovat? At uz prakticka nebo teoreticka.
Jaky je hlavni duvod "generovani" techto novych prvku? Jedna se pouze o poznani nebo maji nove prvky i nejaky prakticky uzitek? Dekuji
Re: hranice
Vladimír Wagner,2016-01-05 14:20:12
Vše závisí na tom, jak těžká jádra mohou ještě existovat. Tedy, jaká je hranice pro počet protonů, že i s tou nejlepší kombinací počtu neutronů, už nevznikne vázaný systém. Vzhledem k tomu, že modely jader nejsou zatím dostatečně přesné a navíc jde o extrapolaci, tak to nedokážeme ani odhadnout. To je ostatně i důvod, proč nedokážeme předpovědět, jakou dobu života mají izotopy supertěžkých prvků na ostrově stability. S největší pravděpodobností musí být kratší než stovka milionů let, protože jinak bychom je museli pozorovat v přírodě. Vznikají totiž určitě při výbuších supernov. Pokud by však byly stabilní v řádu let či dokonce stovek či tisíců let, mohlo by se při nalezení způsobu jejich produkce teoreticky najít i uplatnění. Ovšem v současné době a pravděpodobně i budoucí jde hlavně o poznání toho, jak fungují jaderné síly a jaká je struktura jader. Případně jak se chová systém elektronů okolo tak těžkého jádra a tak intenzivním elektrickém poli.
Relativistické elektrony
Martin Plec,2016-01-05 12:46:04
Díky za článek. Zaujala mě vaše poznámka, že elektrony "se navíc stávají relativistickým". Co je tím míněno? Je to způsobeno velikou hmotnosti jádra, kvůli tomu, že elektrony obíhají moc daleko/blízko jádra, nebo kvůli něčemu jinému?
Re: Relativistické elektrony
Vladimír Wagner,2016-01-05 14:06:40
Není to dáno hmotností, ale nábojem. Jak roste náboj a intenzita elektrického pole, tedy dostředivá síla, musí růst i síla odstředivá, aby byly v rovnováze. A tedy musí růst i rychlost. Dostává se tak do oblasti, kdy se blíží k rychlosti světla. To vysvětlení je nekvantové, tak trochu na úrovni Bohrova modelu, ale princip vysvětluje správně.
Re: Re: Relativistické elektrony
František Bednář,2016-01-06 11:58:20
A nedalo by se tohle zároveň interpretovat jako odpověď na dotaz pana Musila ohledně hypotetické max. hmotnosti jádra atomu ? Tedy jinými slovy hranice leží tam, kde by elektrony musely překonat rychlost světla ?
Re: Re: Re: Relativistické elektrony
Pavel Brož,2016-01-06 14:12:17
Taková hranice daná rychlostí elektronu neexistuje, protože podle speciální teorie relativity se elektrony budou vždycky pohybovat podsvětelnou rychlostí i když se přiblíží libovolně blízko jádru. Pokud by jádro bylo bodové (což navíc není), tak by elektron dosáhl rychlosti světla právě až v okamžiku, kdy by se jej dotkl (tedy když by vzdálenost mezi ním a jádrem byla nulová).
Hypotetický limit na velikost jádra nicméně existuje, nemá ale souvislost s elektronovým obalem, tedy ani s rychlostí elektronů, ale s nábojem jádra. Nukleony jsou v jádře vázány pomocí krátkodosahových sil, které exponenciálně klesají na vzdálenostech větších než je rozměr nukleonu. Oproti tomu elektrická odpudivá síla mezi protony klesá mnohem pomaleji, pouze se čtvercem vzdálenosti. Protože přitažlivá jaderná síla mezi dvěma protony je řádově stokrát větší než odpudivá elektrická, tak do určitého počtu protonů jejich stejný náboj nezpůsobuje nestabilitu jádra. Z podstaty rozdílné rychlosti klesání obou sil se vzdáleností je ale jasné, že někde musí existovat hranice pro počet protonů, nad kterou elektrická odpudivá síla převáží nad jadernou přitažlivou silou.
Ve skutečnosti ale existuje limit i na počet neutronů, ne jenom protonů, díky tomu např. neexistují obří složená jen např. z jediného protonu a mnoha neutronů nebo dokonce jenom z neutronů (s jedinou výjimkou, kterou jsou neutronové hvězdy, které jsou ale dodatečně stabilizované gravitací, kterou v případě normálních jader můžeme zanedbat). V případě limitu na počet neutronů je zapotřebí nasadit sofistikované fenomenologické modely, které takový limit mohou (velice hrubě) určit. I v těchto modelech ale hraje klíčovou roli fakt, že jaderná síla mezi neutrony exponenciálně rychle klesá. Velké jádro se pak tak trochu chová jako kapka vody, která je držena pohromadě krátkodosahovými silami, které se efektivně projevují jako povrchové napětí. I kapka vody je od určité velikosti nestabilní, a v důsledku rotačního či vibračního pohybu se od určité velikosti výše snadno rozpadá na menší kapky.
Re: Relativistické elektrony
Pavel Brož,2016-01-05 22:36:47
Připojuji se k poděkování za velice pěkný článek, a připojuji jen dílčí informaci týkající se relativistických elektronů v atomu.
Důvod, proč jsou elektrony v těžkých atomech relativistické popsal už Vladimír, já k tomu jen dodávám, že úspěšný popis relativistických elektronů v atomu je dodnes plně nedořešeným teoretickým problémem. Nejprve zrekapituluji jak se postupuje v nerelativistickém případě, kde nemáme žádný principiální problém s popisem elektronového obalu atomu. Napíše se nerelativistický Hamiltonián systému, který sestává z nerelativistické kinetické energie plus z potenciální energie, kterou mají elektrony v elektrickém poli jádra plus v poli buzeném ostatními elektrony. Tento Hamiltonián figuruje ve vlnové rovnici, kterou je v tomto případě nerelativistická Schrödingerova rovnice pro n elektronů. Podle kvantové mechaniky jsou energetické hladiny, na kterých mohou elektrony v atomu pobývat, dány tzv. vlastními hodnotami Hamiltoniánu, a tvary elektronových orbitalů (to jsou ony známé "činky" a "preclíky" známé z ilustrací elektronových obalů) jsou pak dány jako tzv. vlastní funkce Hamiltoniánu. Obojí je vlastně svým způsobem čistě matematická úloha - zadá se vhodný operátor, v našem případě Hamiltonián, který by měl mít diskrétní vlastní hodnoty (ty by navíc měly být omezeny zdola, což garantuje existenci základního stavu), a čistě jen matematickými postupy se z něj vyždímají jeho vlastní hodnoty a vlastní funkce. Vlastní hodnoty (tj. energetické hladiny) se fyzikálně dají měřit ze spekter atomů, vlastní funkce (tj. tvary orbitalů) pak promlouvají do takových věcí, jakými jsou např. úhly mezi atomy v chemických sloučeninách, mohou být ale také zkoumány v rozptylových experimentech, atd. atd..
Pro nerelativistický Hamiltonián procedura popsaná výše aspoň principiálně funguje (v reálu se samozřejmě zkonzumuje šílené množství výpočetního času i velice nabušených počítačových klastrů, pakliže-li se má pro velký počet elektronů dojít k výborné shodě s experimentem), a to protože nerelativistický Hamiltonián má spoustu hezkých vlastností, pro které byly už dávno matematicky dokázány takové věci, jako že třeba má diskrétní spektrum vlastních hodnot a že to je navíc omezené zdola (co více si lze přát).
Situace se radikálně mění v okamžiku, kdy se berou v potaz relativistické efekty. Relativistické efekty mohou být zahrnuty buďto nesystematicky jakožto malé korekce k nerelativistické Schrödingerově rovnici, potom výše uvedený postup stále ještě funguje. Z podstaty věci ale takto jde popsat jenom takové elektronové systémy, v nichž se elektrony sice pohybují už "trošku" relativisticky, ale ne moc (čiliž je takto možné dosáhnout pouze jakéhosi "mírného pokroku v mezích zákona", mám-li parafrázovat Jaroslava Haška). Pokud se ale elektrony pohybují "ještě relativističtěji", tak potom už není možné vystačit si s nerelativistickou Schrödingerovou rovnicí dofutrovanou nejnižšími relativistickými korekcemi, ale je nutné pracovat s plně relativistickou vícečásticovou vlnovou rovnicí. A tady nastává hned několik zásadních problémů.
Prvním z nich je, jaká že by to měla vlastně být rovnice. Často se pracuje např. s vícečásticovou Diracovou rovnicí, existují ale i jiné přístupy, pracující např. se zobecněním Bethe–Salpeterovy rovnice anebo Breitovy rovnice (proč není jednoznačně dané, která z nich by to měla být, zmíním později). Mnohem větším problémem je, že ani pro jednu z nich není dodnes dokázáno ono nezbytné minimum, které požaduje, aby tyto rovnice vedly k diskrétnímu a zdola omezenému spektru vlastních hodnot. Ba dokonce - ó hrůzo!!! - se pro některé z nich podařilo matematicky exaktně dokázat pravý opak, totiž že žádné takové diskrétní a zdola omezené spektrum vlastních hodnot nemají (viz např. článek "Spectral problems about many-body Dirac operators mentioned by Derezinski" na http://arxiv.org/pdf/1403.6900.pdf).
Nyní se zmíním o tom, proč není tak jednoznačné určit, jaká že to relativistická rovnice by měla správně nahradit Schrödingerovu rovnici, pokud chceme adekvátně popisovat relativistické elektrony v supertěžkých atomech. Problém je v tom, že ať už nerelativistická či už nějaká hypotetická relativistická vlnová rovnice může popsat pouze konečný počet částic, v daném případě elektronů - říkáme, že popisujeme kvantově MECHANICKÝ systém, tedy že pracujeme s kvantovou MECHANIKOU. Jakmile se ale vezmou v potaz i relativistické efekty, nutně tam začnou hrát roli i kvantově POLNÍ efekty, jako jsou např. efekty působené vznikem a zánikem virtuálních částic (ty způsobují mj. i takové měřitelné efekty, jako třeba tzv. Lambův posun či hyperjemné rozštěpení energetických hladin, ale také třeba Casimirův efekt aj.). Takové systémy jsou v principu systémy s nekonečným počtem částic, proto už nehovoříme o kvantové mechanice, ale o kvantové teorii pole.
Uspokojivou kvantovou teorii pole máme (dokonce nejen pro elektromagnetickou, ale i pro slabou a silnou interakci). Pro popis elektronového obalu můžeme s klidem zanedbat slabé a silné interakce a vystačit si s kvantovou elektrodynamikou, což je kvantová teorie pole popisující elektromagnetické procesy. Mohli bychom si tedy říct, že prostě vezmeme kvantovou elektrodynamiku, uděláme patřičná přiblížení, a získáme správnou relativistickou alternativu k nerelativistické Schrödingerově rovnici. Tímto postupem opravdu v případě dvou částic postupovat lze, získá se tak např. výše zmíněná Breitova rovnice, která se excelentně osvědčila pro předpověď energetických hladin např. pozitronia, vázaného systému složeného z elektronu a pozitronu. Pro více částic se ale naráží na celou řadu zcela zásadních technických komplikací. A aby toho nebylo málo, tak se dá navíc matematicky exaktně ukázat, že kvantová teorie pole ve čtyřech a více prostoročasových dimenzích (což je na potvoru případ i našeho prostoročasu) v principu neumožňuje popis jakýchkoliv vázaných stavů, tedy ani stabilního elektronového obalu. Trošku to působí dojmem, že démon vymyšlený tvůrcem klasické elektrodynamiky si našel úplně jinou doménu svého působení a zpupně se nám chechtá.
Takže toto je v kostce lesk a bída relativistické kvantové teorie vázaných stavů. Do budoucna to obnáší velice slibné pole výzkumu, na kterém bude ale nezbytné přemoct mnoho dodnes otevřených a dnes neřešitelných problémů. Dokonce není ani vyloučeno, že průlom v této oblasti bude přenositelný do popisu ještě mnohem komplikovanějších relativistických vázaných stavů, kterými jsou právě vázané stavy nukleonů v atomových jádrech či vázané stavy kvarků v nukleonech či mezonech.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce