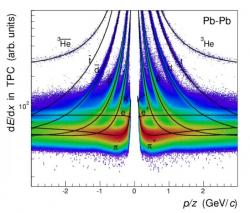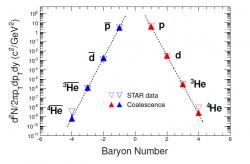
Při srážkách těžkých jader na urychlovači LHC se velká část jejich kinetické energie přemění na hmotnost (klidovou energii) nových částic. Přesně podle známého Einsteinova vztahu E=mc2. Při této velmi intenzivní produkci nových částic vzniká stejný počet částic a antičástic, v daném případě kvarků a antikvarků. Vzniká velice horká a hustá jaderná hmota ve fázi kvark-gluonového plazmatu. Při jeho ochladnutí se kvarky a antikvarky musí spojit do částic označovaných jako hadrony, tedy hadrony i antihadrony (blíže o zoologii elementárních částic zde). Mezi ně patří protony a neutrony i antiprotony a antineutrony. Horká a hustá jaderná hmota se pak dále rozpíná a chladne. Částice se rozlétají. Může se však stát, že proton a neutron jsou velmi blízko sebe a letí téměř stejným směrem a stejnou rychlostí, jejich pohyb vůči sobě je natolik malý, že se spojí do deuteronu. Totéž může nastat i pro antiproton a antineutron a vznikne tak antideuteron. Pravděpodobnost těchto událostí je velmi malá, ale srážek jader olova na LHC je extrémní množství, takže se i tak vyprodukuje velký počet deuteronů a antideuteronů. A dokonce vznikají i jádra se třemi nukleony. Může jít o triton, tedy velmi těžký vodík, který má jeden proton a dva neutrony. V případě antitritonu pak jeden antiproton a dva antineutrony. Nebo o lehký izotop hélia tři se dvěma protony a jedním neutronem. Zatím nejtěžším antijádrem, které se podařilo takto získat, je antihélium 4, poprvé to bylo na urychlovači RHIC v americkém Brookhavenu (zde). Ovšem s každým dalším nukleonem klesá pravděpodobnost produkce jádra o tři řády (viz obrázek). Další antijádro už tak představuje značný problém. Neexistuje jádro (a tedy i antijádro) s pěti nukleony. Další by pak muselo mít nukleonů šest (třeba lithium 6 se třemi protony a třemi neutrony). Ale produkce antilithia 6 by byla o šest řádů, tedy milionkrát méně pravděpodobná, než produkce antihelia 4. A to je zatím nepřekonatelná překážka.

Velice podrobnou analýzu velkého množství dat o lehkých jádrech a antijádrech, které se nashromáždilo při srážkách jader olova v experimentech první etapy provozu urychlovače LHC, provedli fyzikové experimentu ALICE. Tato detektorová sestava obsahuje velmi silný magnet, jehož magnetické pole o intenzitě zhruba 0,5 T silně zakřivuje dráhu letu nabitých částic. Uvnitř něj jsou detektory, které umožňují velice přesně tuto dráhu zobrazit. Z ní je pak možné jádro či částici identifikovat a také velice přesně určit poměr hmotnosti a náboje. Ještě přesněji než absolutní hodnotu tohoto poměru u jádra a antijádra lze určit rozdíl tohoto poměru mezi nimi. V tomto případě se odstraňuje řada zdrojů nepřesností a získá se tak velice přesné určení rozdílu v této hodnotě u jádra a antijádra. Podařilo se tak zjistit, že rozdíl je na úrovni desetiny procenta a menší.
Takto přesnou hodnotu rozdílu poměru hmotnosti a náboje se podařilo zjistit u deuteronu a antideuteronu i u helia 3 a antihélia 3. Byla to pěkná oslava padesátého výročí první produkce antideuteronu na protonovém synchrotronu v americkém Brookhavenu i v samotné laboratoři CERN v roce 1965. Přesně určený rozdíl poměru hmotnosti a náboje u jádra a antijádra a dříve s velikou přesností určené hodnoty rozdílu hmotnosti protonu a antiprotonu i neutronu a antineutronu umožňují také zjistit rozdíl vazebné energie pro jádro a antijádro. Zjištěné rozdíly pro poměr hmotnosti a náboje i vazebnou energii jsou ukázány na obrázku.
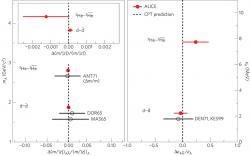
Tyto výsledky doplnila velice přesná měření, která nedávno uveřejnil experiment BASE (Baryon Antibaryon Symmetry Experiment). Ten využívá cernský zpomalovač antiprotonů. Podařilo se mu prokázat, že poměr náboje a hmotnosti je u protonu a antiprotonu stejný s přesností 69∙10-12. Metodu, kterou využili, bylo srovnání cyklotronové frekvence antiprotonu a záporného iontu vodíku se dvěma elektrony. Měření prováděli v magnetické pasti s intenzitou magnetického pole 1,95 T. Je tak vidět, že kombinace různých experimentů v laboratoři CERN se vzájemně doplňují a přinášejí špičkové výsledky.
Proč je to důležité?
Principiální důležitost měření těchto veličin je dána tím, že ukazují na dodržování fundamentálních symetrií v přírodě. Těmito symetriemi jsou zrcadlová symetrie, označovaná také jako P symetrie. Ta platí, když se fyzikální zákonitosti zachovají při zrcadlovém zobrazení. Tedy, že svět v zrcadle se nedá rozeznat od normálního světa. Dále jde o C-symetrii. Ta platí, když se fyzikální zákonitosti nezmění v případě záměny částic za antičástice a naopak. Tedy, že svět nelze rozeznat od antisvěta. Třetí je pak T-symetrie, která platí, když se fyzikální zákonitosti nezmění při záměně směru toku času. Postupně se ukázalo, že se narušuje P-symetrie a také C-symetrie. Dále také, že se narušuje i kombinovaná CP-symetrie. Speciální teorie relativity vyžaduje, aby se zachovávala kombinovaná CPT-symetrie. Jestliže se narušuje CP-symetrie, musí tak být toto narušení kompenzováno narušením T-symetrie. Právě porovnání rozdílu poměru hmoty a náboje u objektu z hmoty a objektu z antihmoty velice přesně testuje zachování CPT-symetrie. Pokud by se pozoroval rozdíl, znamená to její narušení. Podrobněji o těchto symetriích a jak lze jejich narušení využít pro to, abychom vzdáleným mimozemšťanům sdělili, která strana je levá a která pravá i to, že jsme z hmoty a ne antihmoty je popsáno zde. Stále přesnější měření hmotností, poměru hmotnosti a náboje částic a antičástic i jader a antijader umožňuje prokázat, že fyzika těchto objektů, tedy i interakcí, které v nich působí, zachovává CPT-symetrii s velmi vysokou přesností. Daří se tak vylučovat některé hypotézy exotické fyziky za Standardním modelem.
Na závěr bych si dovolil osobní poznámku. Na experimentu ALICE intenzivně pracují i fyzikové z Česka, hlavně z Ústavu jaderné fyziky AV ČR a FJFI ČVUT. Své diplomové i PhD práce zde dělají i naši studenti. Podílejí se i na práci spolupráce STAR v americkém Brookhavenu. Já osobně jsem se maličko podílel na budování ALICE a na počáteční fázi jejího experimentování. Teď už její práce sleduji spíše zpovzdálí. Právě proto svým kolegům a kamarádům k tomto výsledku moc a hrozně rád gratuluji.
Literatura
Publikace ALICE: http://www.nature.com/nphys/journal/vaop/ncurrent/full/nphys3432.html
Publikace BASE: http://www.nature.com/nature/journal/v524/n7564/full/nature14861.html
Video: Význam experimentálního výsledku
Podivnosti kvantového světa
Autor: Vladimír Wagner (21.06.2010)
První srážky s energií 13 TeV na urychlovači LHC
Autor: Vladimír Wagner (23.05.2015)
Diskuze:
Dotaz-rezonance a vnucené rezonance
Jaroslav Mrázek,2015-08-19 09:19:17
Lze jimi docílit jiných hodnot i u stabilních a zdánlivě neměnných veličin?
různá míra narušení symetrií
Pavel Brož,2015-08-19 00:23:45
Vysoká přesnost zachování CPT symetrie je bezesporu pěkná vlastnost z hlediska jednoduchosti či elegance fyzikálních zákonů, a to bez ohledu na to, že hatí naděje autorů některých exotičtějších fyzikálních teorií. Na druhou stranu je dobré mít na paměti, že i ty symetrie, které se nezachovávají, konkrétně P symetrie a CP symetrie, tak činí dosti rozdílnou měrou. Zatímco v případě slabých interakcí je P symetrie narušena maximální možnou měrou, což se projevuje mj. tím, že existují jen levotočivá neutrina a žádné pravotočivé neutrino (exaktněji řečeno – případná pravotočivá neutrina, tzv. sterilní, se neúčastní slabých interakcí, mohou tedy interagovat maximálně tak gravitačně), tak v případě CP symetrie je už její narušení mnohem subtilnější, v řádu tisícin. Proto výsledek, že CPT symetrie platí s přesností řádově 10^-11 je určitě dobrá zpráva, ale pořád může existovat narušení ještě menší.
Jako jistou vzdálenější analogii můžeme vzít poměry hmotností elementárních částic. Dlouhou dobu se mělo za to, že neutrina mají přesně nulovou hmotnost, dnes už se ví, že minimálně dvě z nich hmotnost mají. Přitom hmotnost elektronového neutrina jakožto nejlehčí hmotné částice je menší, než řádově 10^-11 hmotnosti nejtěžší známé elementární částice, kterou je top kvark.
Tím nechci říct, že poměr hmotnosti nejlehčí a nejtěžší známé hmotné částice má něco společného s mírou narušení CPT invariance, tím chci jen poukázat na to, že fyzika elementárních částic umí bez problémů absorbovat i rozdíly mnoha řádů. Narušení CPT invariance se ve skutečnosti očekává dříve či později (adekvátněji řečeno, v míře extrémně malé či ještě menší, ale určitě v nějaké nenulové míře). Existují pro to i celkem rozumně znějící argumenty v podobě efektů působených gravitačními fluktuacemi na extrémně malých vzdálenostech, na které se ještě hodně dlouho nebudeme umět našimi experimenty dostat. Podle současných představ bychom tyto efekty měli potkat nejpozději na Planckově škále, nicméně právě proto, že fyzika elementárních částic tak snadno překlenuje i rozdíly deseti či více řádů, tak zdaleka není jasné, na jaké že škále je máme vlastně očekávat (a spolu s nimi i narušení CPT). Osobně si myslím, že nám stále ještě několik řádů k odhalení narušení CPT symetrie schází, a tedy že dost dobře možná ještě ani příští generace fyziků se takového objevu nedožije, na druhou stranu ale nepochybuji o tom, že jednou bude i tato symetrie oficiálně uznána za narušenou.
Re: různá míra narušení symetrií
Pavel A1,2015-08-23 19:02:08
Pokud je mi známo, tak zachování CPT symetrie je přímý důsledek invariance vůči Lorentzově transformaci. Tedy pokud by byla narušena CPT symetrie, byla by narušena Lorentzova symetrie a tedy by byla popřena teorie relativity. Ano, jsou teorie, které předpokládají narušení Lorentzovy symetrie (třeba smyčková gravitace), ale experimentálně bylo dokázáno, že tato symetrie platí s přesností o několik řádů větší než tyto teorie předpokládají. Nevím o žádné teorii, která předpokládá narušení Lorentzovy invariance a nebyla by experimentálně vyvrácena.
Re: Re: různá míra narušení symetrií
Pavel Brož,2015-08-26 22:06:54
Lorentzovská invariance musí být nutně narušena, pokud bereme vážně kvantově gravitační efekty, které mají nastávat na nějaké dostatečně malé škále, za kterou dnes považujeme Planckovu délku. Pokud by Lorentzova invariance platila bez omezení na libovolně malé délce, pak by nastal dost nepříjemný problém, kvantově gravitační efekty by nastávaly pro pozorovatele pohybující se různou rychlostí na různých škálách. Samotná speciální teorie relativity jako taková z principu nemá a ani nemůže mít žádný limit na energie, protože každá částice může mít libovolně velkou energii v závislosti na tom, v jaké soustavě je pozorována. Oproti tomu ve všech kvantových teoriích gravitace jistá mezní energie existuje, je jí Planckově energie, kterou můžeme vyjádřit jako konstantu, která je nepřímo úměrná právě zmíněné Planckově délce (E_p=h_bar*c/l_p, kde E_p je Planckova energie, h_bar je redukovaná Planckova konstanta, c je rychlost světla a l_p je Planckova délka). Právě tato energie vnáší význačnou energetickou škálu do jinak energeticky bezškálové speciální teorie relativity. Jinými slovy můžeme říct, že platnost přesné Lorentzovy invariance na libovolně malé vzdálenosti vyžaduje dokonalou absenci energetických a tím i délkových škál, což lze bez problémů splnit v klasické, nekvantové speciální relativitě, ne ale v prakticky jakékoliv mainstreamové teorii kvantové gravitace, protože prakticky všechny předpokládají existenci energetické a délkové škály.
Takže je to přesně naopak než píšete – ne že by narušení Lorentzovy invariance a s ní spojené narušení CPT invariance předpokládala jen smyčková gravitace, případně nějaké jiné extrémně radikální teorie kvantové gravitace, ale naopak prakticky všechny teorie kvantové gravitace předpokládají na jisté škále narušení Lorentzovy invariance a s ní i narušení CPT. Jde pouze o to, že drtivá většina těchto teorií předpokládají toto narušení na extrémně malé škále, čili pro extrémně vysoké energie částic. A protože Planckova energie je rovna zhruba 1,2*10^28 eV, což je energie o patnáct řádů větší, než energie dosahovaná na LHC, tak je jasné, že ještě hóóódně dlouho mohou být experimentátoři co se týče těchto efektů v klidu. A pokud vezmeme v potaz myšlenku vyjádřenou v mém předchozím příspěvku, konkrétně že fyzika elementárních částic umí ve specifických případech překlenout i rozptyl deseti či více řádů pro hodnoty stejného druhu (jako příklad jsem uvedl rozptyl hmotnostního spektra elementárních částic, jako jiný příklad lze uvést např. roztyl mezi typickými časovými škálami pro silné, elektromagnetické a slabé interakce), tak nemůžeme vyloučit to, že kvantově gravitační efekty nemusí být až těch patnáct řádů daleko od současných možností. Pokud jsou kvantově gravitační efekty patnáct řádů nad současnými možnostmi, tak prakticky není šance, aby byly pozorovány v příštích sto letech. Pokud jsou ale shodou okolností jen třeba pět řádů daleko, tak existuje aspoň šance, že za několik desítek let se třeba objeví nějaká revoluce v urychlování částic, která nám umožní tyto efekty pozorovat. Narušení CPT by pak bylo v řádu zhruba 10^-16, tedy výrazně menší, než v článku zmíněných 10^-11, nicméně bylo by nenulové.
Re: Re: Re: různá míra narušení symetrií
Pavel A1,2015-08-27 19:55:42
To co popisujete je neduh všech teorií, které se snaží popsat kvantovou gravitaci pomocí kvantování prostoru a času. Ty trpí problémem, že ta kvanta jsou pro různé pozorovatele různě velká. Z těchto teorií obecně vyplývá, že rychlost světla není konstantní, ale závisí na energii fotonů. Před pár lety ale bylo pozorováno několik gama záblesků s velmi vysokou energií fotonů a z toho vyplynulo, že pokud nějak závisí rychlost fotonů na jejich energii, tak je ta závislost tak malá, že charakteristická vzdálenost, na které se projevuje kvantová gravitace, by musela být o několik řádů menší, než je Planckova délka. A už i přední představitelé těchto teorií připustili, že to je pro ně průšvih a že Vesmír je invariantní vůči Lorentzově transformaci.
Existuje ale kvantová teorie gravitace, která nepotřebuje kvantovat čas a prostor, je zcela Lorentz-invariantní a přesto konzistentně popisuje gravitaci jak makroskopicky, tak i mikroskopicky - teorie strun. V té je naopak přesná invariance vůči Lorentzově transformaci jeden ze základních předpokladů. Já proto předpokládám, že narušení CPT symetrie nebude nikdy zjištěno.
Ostatně za pár let můžeme být moudřejší. Chystá se několik experimentů, které mají CPT symetrii prověřit. Jeden z nich je měření elektrického dipólového momentu elektronu. Pokud platí CPT symetrie, měl by být přesně nula. Tento experiment by měl být dokončen v dohledné době.
Re: Re: Re: Re: různá míra narušení symetrií
Pavel Brož,2015-08-28 00:07:11
Velice se omlouvám, ale bohužel některá Vaše tvrzení si zaslouží větší či menší korekci, vezmu to postupně.
Především mnou popisované příklady narušení Lorentzovy invariance v důsledku existence energetické škály automaticky neimplikují, že se bavíme o teoriích zavádějících nějaká kvanta prostoru a času. Kromě Vámi prve zmíněné smyčkové gravitace totiž Lorentzovu invarianci narušují také např. tyto teorie:
Very special relativity (https://en.wikipedia.org/wiki/Very_special_relativity)
Double special relativity (https://en.wikipedia.org/wiki/Doubly_special_relativity)
nekomutativní kvantové teorie pole (https://en.wikipedia.org/wiki/Noncommutative_quantum_field_theory)
teorie indukované gravitace (https://en.wikipedia.org/wiki/Induced_gravity)
Hořavova-Lifšicova teorie (https://en.wikipedia.org/wiki/Ho%C5%99ava%E2%80%93Lifshitz_gravity)
(mimochodem Petr Hořava, svého času také kolega Edwarda Wittena, je jedním z prvních českých průkopníků strunových teorií, k nimž nemalou měrou přispěl)
a kromě toho se narušení Lorentzovy invariance běžně objevuje i ve Vámi zmiňovaných strunových teoriích, viz např.:
String Theoretic Bounds on Lorentz-Violating Warped Compactification - http://arxiv.org/pdf/hep-th/0301189.pdf
Background Dependent Lorentz Violation from String Theory - http://arxiv.org/pdf/1110.0451.pdf
String Quantum Gravity, Lorentz-Invariance Violation and Gamma-Ray Astronomy - http://arxiv.org/pdf/1010.5354.pdf
Lorentz Invariance Violation from String Theory - http://arxiv.org/pdf/0708.2250.pdf
A New Lorentz Violating Nonlocal Field Theory From String-Theory - http://arxiv.org/pdf/hep-th/0609107.pdf
Žádná z teorií vyjmenovaných v tomto seznamu nezavádí žádná kvanta prostoru a času, a přesto narušení Lorentzovy invariance obsahuje. Také není pravda, že z těchto teorií automaticky vyplývá závislost rychlosti světla na energii fotonu – toto je pravda např. pro smyčkovou gravitaci, kterážto její předpověď se dostala do rozporu s měřeními Vámi zmíněných vysoce energetických gama záblesků, nejedná se ale o obecnou vlastnost společnou všem teoriím obsahujícím narušením Lorentzovy invariance.
Co se týče teorie strun jakožto teorie prosté efektů narušujících Lorentzovu invarianci, tak to také není pravda, jak plyne mj. i z výše uvedených strunových článků. Tady je dobré zmínit důležitou okolnost – strunová teorie není nějakou unikátní logicky konzistentní teorií, spíše se jedná o teoretický rámec, v rámci kterého lze teprve nalézt konkrétní teorie v závislosti na specifikaci spousty pro předpovídané výsledky zcela zásadních věcí, mezi nimiž hraje roli třeba to, které objekty v teorii vystupují (zda jenom struny, a pokud jen ony, zda otevřené, uzavřené nebo obojí, anebo zda zde vystupují i vícerozměrné tzv. brány), dále zda tyto objekty existují pouze v mikroskopickém, či i v kosmologickém měřítku (podle některých variant strunových teorií může např. celý náš Vesmír sestávat z jedné takové čtyřrozměrné brány, kterých přitom ve vícerozměrném multiverzu může existovat neomezeně mnoho), dále kolik existuje dimenzí celkově (zda deset nebo jedenáct) a kolik z nich je kompaktifikovaných do extrémně malých tzv. Calabiho variet (v původních strunových teorií bylo šest, resp. později sedm, kompaktifikovaných, v dnešních scénářích už toto omezení dávno neplatí, mohou existovat i tzv. „velké“ extra dimenze, za předpokladu, že žijeme např. na nějaké čtyřbráně vnořené ve větším multiverzu), a v neposlední míře záleží na tom, jakým způsobem případná kompaktifikace nadbytečných dimenzí proběhla (existuje totiž až cca 10^500 různých kompatifikací a jim odpovídají různé finální strunové teorie, navzájem se výrazně lišící předpovídanými výsledky – jinými slovy, ať už byste od začátku Velkého Třesku bez přestání měřil a měřil a měřil, tak by Vám dodnes zbývalo prakticky neomezené množství strunových teorií, které by se do výsledků všech Vašich měření pořád vešly).
Navíc strunové teorie stejně tak jak nestrunové teorie mohou volitelně zavést celou řadu mechanismů, včetně velice oblíbeného spontánního narušení symetrie, které může, či nemusí, podle volby modelu, vést k narušení Lorentzovy invariance, viz např. mnou citované strunové články. Takže není pravda, že strunové teorie jsou zcela Lorentzovsky invariantní, to totiž závisí na mnoha dalších mechanismech, které se do té které strunové teorie zahrnou či nezahrnou.
Co se týče tvrzení, že Vesmír je invariantní vůči Lorentzově transformaci, tak toto tvrzení v této podobě není pravdivé. Náš Vesmír je totiž popisován rozpínajícím se řešením Einsteinových rovnic, a toto řešení NENÍ Lorentzovsky invariantní. Jedná se o situaci analogickou ke spontánnímu narušení symetrie, kdy se také setkáváme se situací, že pohybové rovnice jsou invariantní vůči nějaké symetrii, ale konkrétní řešení už tuto symetrii nemá. U kosmologických řešení Einsteinových rovnic jde o totéž – Einsteinovy rovnice jsou Lorentzovsky invariantní, ale jejich řešení popisující rozpínající se Vesmír už Lorentzovsky invariantní není. Díky tomu můžeme zavést v každém bodě lokální preferovanou pozorovací soustavu, a to soustavu, vůči které se okolní Vesmír rozpíná rovnoměrně. Jakmile bychom místo toho přešli do jiné soustavy, která se vůči té preferované pohybuje, tak to spolehlivě poznáme podle toho, že v jednou směru naměříme v průměru menší červené posuny vzdálených galaxií než ve směru opačném. Tohleto je věc, která málo zmiňovaná v popularizačních výkladech speciální a obecné relativity – zatímco speciální teorie relativity zrušila význačnou preferovanou soustavu (tehdy spojovanou s tzv. éterem, hypotetickým prostředím, jehož kmity byly ztotožněny s elektromagnetickými vlnami), a zatímco obecná teorie relativity tuto rovnoprávnost navzájem se pohybujících soustav převzala při popisu „lokálních“ (ve smyslu „nekosmologických“) jevů, tak tatáž obecná teorie relativity nakonec znovu vnesla privilegovanou soustavu spojenou se svým kosmologickým řešením, které popisuje náš rozpínající se Vesmír. Takže ano, obecná teorie relativity je Lorentzovsky invariantní, ale ne, náš Vesmír není Lorentzovsky invariantní.
No a co se týče elektrického dipólového momentu, tak bohužel také není pravda, že by měl být přesně nula pokud platí CPT invariance. Elektrický dipólový moment vychází nenulový i ve Standardním modelu, pro který platí CPT invariance. Vychází ale malý, asi o devět řádů menší, než vychází ze současných měřených limitů (viz např. zde https://en.wikipedia.org/wiki/Electron_electric_dipole_moment). V některých rozšířeních Standardního modelu, např. v technicolorových teoriích, vychází ta hodnota řádově srovnatelná se současnými experimentálními limity, v jiných rozšířeních, např. v některých supersymetrických modelech, vychází dokonce větší, než jsou tyto limity. Jinými slovy některé supersymetrické modely (těch ovšem existuje velice hodně variant) už byly vyřazeny měřením elektrického dipólového momentu, jiná rozšíření, např. některé z technicolorových modelů, mohou být brzo vyřazeny po Vámi zmíněném zpřesnění měření. Dobré je ovšem vědět, že jak technicolorové teorie, tak supersymetrická rozšíření Standardního modelu jsou CPT invariantní, nenulový elektrický dipólový moment v nich vzniká (stejně jako ve Standardním modelu) nikoliv v důsledku narušení CPT, ale v důsledku radiačních korekcí ve vyšších řádech poruchové teorie. Ve Standardním modelu vychází nenulovost elektrického dipólového momentu elektronu až ve Feynmanových diagramech obsahujících nejméně čtyři smyčky, zatímco v některých rozšířeních Standardního modelu jako jsou ty technicolory nebo supersymetrické modely vycházejí už v nižších Feynmanových diagramech, a proto v nich vychází ten dipólový moment větší než ve Standardním modelu. Kauzální souvislost s CPT zde není – nové měření zkrátka vyřadí nějaké malé procento z obrovského množství konkurujících si teorií, z čehož některé z takto vyřazených teoriích jsou CPT invariantní, jiné nejsou, a stejně tak některé z teorií, které přežijí, jsou CPT invariantní, zatímco jiné nejsou. Celkový enormní počet teorií se nijak neumenší, protože neustále vznikají nové.
Neberte to prosím nijak zle, pouze jsem chtěl některé věci upřesnit.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce