Kvanta nebo relativita? To nejzajímavější z fyziky se dneska děje na frontové linii mezi dvěma velice užitečnými a stále naprosto nesmiřitelnými způsoby vidění světa –
kvantovou mechanikou a obecnou relativitou. Je to neobyčejně zvláštní válka, snad nikdo si totiž nepřeje, aby jedna ze stran konfliktu přesvědčivě zvítězila. Dva základní myšlenkové rámce dnešní fyziky se střetávají za sršení mračen hypotéz v nepředstavitelném nitru černých děr, v šílenství exploze Velkého třesku a kupodivu také v legendárním cestování časem.

Jak známo, obecná relativita krotí hvězdy a galaxie na ohromných měřítcích, před nimiž naše fantazie bledne. Stejně tak ovšem bledne nad jevy extrémními v opačném směru, ve světě molekul, atomů a elementárních částic, s nimiž pracuje kvantová mechanika. Podle Tima Ralpha z Queenslandské univerzity a jeho kolegů se problematika cestování časem motá právě kolem třecí plochy relativity a kvantové mechaniky, což ji činí obtížně uchopitelnou a zároveň ještě více vzrušující.
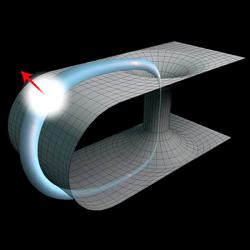
Po tolika letech to zní stále jako science fiction, ale Einsteinovy rovnice v jistém úhlu pohledu nevylučují cesty časem. Jen to chce cestovat časoprostorem po uzavřených časupodobných křivkách (CTC, Closed Timelike Curves). Pohyb časoprostorem lze znázornit světočárou (world line) na časoprostorovém diagramu a uzavřená časová křivka je světočára hmotné částice, která se vrací v čase zpět do výchozího bodu. Odborník by dodal, že se to odehrává ve čtyřrozměrné lorentzovské varietě (Lorentzian manifold), ve které lze podle obecné relativity úspěšně modelovat časoprostor.
S uzavřenými časovými křivkami přišel poprvé Kurt Gödel, když v roce 1949 vynalezl řešení rovnic obecné relativity, známé jako Gödelova metrika. Od té doby se objevila i další řešení obsahující uzavřené časové křivky, například Tiplerův válec anebo průchozí červí díra. Byť jen velice teoretická možnost cestování časem od samotného počátku nesmírně dráždí fyziky i filozofy, protože vyvolává na světlo znepokojivé paradoxy. Znáte to, co kdyby jste se vrátili časem a rozmluvili vlastnímu dědečkovi svatbu s babičkou, pokud by jste ho rovnou pro jistotu nesprovodili ze světa?
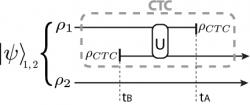
Tim Ralph je přesvědčen, že cestování časem ve světě kvantové mechaniky dovoluje podobné paradoxy obcházet. Jednoduše řečeno, kvantové vlastnosti částic jsou natolik neurčité, že zbývá prostor na kličkování mezi rozpory a paradoxy cestování časem. Ralph sice přiznává, že jsme ve kvantovém světě zatím nepozorovali chování, které by se lišilo od předpovědí standardní kvantové mechaniky, jedním dechem ale dodává, že jsme to netestovali v prostředí extrémních jevů z hájemství obecné relativity, jako je třeba okolí černé díry.
Aniž by měli k dispozici stroj času, Ralph a spol. se do toho pustili experimentálně. V důmyslném experimentu simulovali cestování časem pomocí jednotlivých fotonů, což ji umožnilo přiblížit se jevům, které by se odehrávaly v souvislosti s uzavřenými časovými křivkami. Jak by se dalo čekat, jde opět o velice vzrušující záležitosti, včetně možnosti narušení Heisenbergova principu neurčitosti, rozbití kvantové kryptografie nebo dokonalé klonování kvantových stavů.
Through the wormhole with Morgan Freeman S01E03 Is time travel possible?. Kredit: MMX Discovery.
Literatura
University of Queensland/ Faculty of Science News 19. 6. 2014, Nature Communications 5: 4145 (online 19. 6. 2014), Wikipedia (Closed tímelike curves, Lorentzian manifold).
Diskuze:




