Budiž to už trochu neoriginální poctou Tolkienovi s Jacksonem, ale jen máloco vystihuje temnou hmotu tak přesně, jako jedna z Glumových hádanek ve tmě: „Není ji vidět, není ji cítit, není ji slyšet, nejde ji chytit. Je za hvězdami a pod horami a vyplňuje prázdné jámy. Byla tu předtím a přijde pak a nakonec ti vytře zrak.“ Jak trefné! Teď se objevila možnost, že je to ještě horší. Možná už totiž o té proklaté temné hmotě nějakou dobu víme, jen jsme si to zatím neuvědomili.
Prozatím je to taková astrofyzikální provokačka, kterou sám sepsal Christian Beck z Institutu matematických věd Isaaca Newtona z Univerzity v Cambridgi. Dotyčný matematik je momentálně na sabatiklu, čili tvůrčí dovolené a tak se není moc čemu divit. Podle Becka by temnou hmotou mohly být axiony, tedy oficiálně hypotetické částice, které v roce 1977 navrhli Peccei a Quinová jako řešení problému s CP symetrií ve kvantové chromodynamice. Od těch dob se vědci snaží nalézt axiony v celé řadě rozmanitých experimentů, zatím ovšem bezúspěšně. Axiony jsou navrženy tak, že nemají žádný elektrický náboj, mají jen zcela nepatrnou hmotnost a také jen velmi omezeně interagují se silnou a slabou jadernou silou. To z nich dělá jen velmi obtížně zjistitelné mrchy, pokud samozřejmě vůbec existují. Když axiony projdou silným magnetickým polem, tak se mohou proměnit na fotony a naopak. Zároveň jsou axiony už delší dobu mezi nejvíce žhavými kandidáty na temnou hmotu, takže by to vlastně nebylo moc velké překvapení.
O co vlastně jde? V experimentech se supravodivostí se objevuje jistá anomálie, kterou by podle provokujícího Becka mohly způsobovat procházející axiony. Pokud by Beck měl pravdu, tak vědci v těchto experimentech zachytili axiony o hmotnosti 0,11 meV/c na druhou, čili o váze odpovídající 2 krát 10 na mínus 10 hmotnosti běžného elektronu. Perfektní představa. Prozatím je ale na místě velká opatrnost. Potvrzení prolomení nejzarytější vědecké záhady posledních desetiletí si bude žádat víc, nežli jeden text výstředního vědce. Na druhou stranu, bádaní kolem temné hmoty je už natolik zamotané, že by Beckovo řešení mnozí uvítali jako úžasný dárek pod astrofyzikální stromeček.
Aktuální situace vypadá následovně. Zvláštní jevy v supravodivých experimentech nemusejí vyvolávat axiony. Může za tím být něco úplně jiného, s temnou hmotou nesouvisejícího. Nicméně, Beck vyslovil zajímavou a prý relativně snadno testovatelnou hypotézu. Zmíněné experimenty se supravodivostí nejsou nijak závratně nákladné a nevyžadují bizarní, veliké a často podzemní detektory, tak jako tomu je například při pátrání po dalších kandidátech na temnou hmotu, netečných a těžkých wimpech. Navíc by prý mělo být relativně snadné rozlišit šum v přístrojích způsobený axony od šumu méně exotického původu.
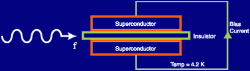
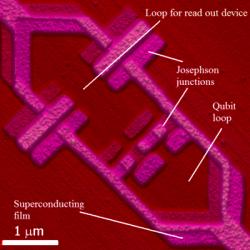
Jestli se Beck nemýlí, tak bychom měli ulovit axiony pomocí takzvaných Josephsonových přechodů (Josephson junction). To jsou mikroskopické elektronické součástky, které sestávají ze dvou supravodičů, oddělených tenkou vrstvou izolantu. Dochází v nich k takzvanému Josephsonově jevu, čili ke vzniku elektrického proudu mezi supravodiči, skrz izolant, za normálních okolností neprostupný. Když, podle Becka, axion vstoupí do vrstvy izolátoru Josephsonova přechodu a energie vyplývající z jeho hmotnosti odpovídá Josephsonově frekvenci, tak to vyvolá nárůst elektrického proudu v dotyčném Josephsonově přechodu. Axiony se v Josephsonově přechodu přemění na fotony, ty zesílí supravodivost systému a při odchodu se zase přemění zpět na axiony.
Beck přitom vychází z anomálií, které popsali Hoffmann a spol. v roce 2004 i další výzkumné týmy při experimentech s Josephsonovými přechody. Vědci se zmiňují o šumu v Josephsonových přechodech, který lze z části vysvětlit známými jevy. Při určité energii ale tento šum dramaticky naroste a přitom není jasné proč. Zatím nikdo nepřišel s uspokojivým vysvětlením a mělo se za to, že odpověď nějakým způsobem souvisí s teorií supravodivosti. Beckův nápad by mělo jít relativně snadno ověřit. Stačí jenom Josephsonovův přechod izolovat od možných zdrojů šumu a pak se dívat, jestli to mělo nějaký vliv. Axiony projdou zcela v pohodě prakticky čímkoliv, takže je odstínit nelze. Působení axionů také bude možné zamítnout ve chvíli, kdy se ukáže, že energie pozorovaného jevu v šumu na Josephsonových přechodech není stálá. Nic z toho přitom není závratně technicky či myšlenkově náročné. Takže, axiony střezte se. Pokud jste podstatou temné hmoty, tak už vás máme skoro v hrsti!
Literatura
Ars Technica 5. 12. 2013, Physical Review Letters 111: 231801, Wikipedia (Axion, Josephson effect).
Pochází temná hmota z Temného Velkého třesku?
Autor: Stanislav Mihulka (21.11.2024)
Supermasivní černá díra v raném vesmíru hltá hmotu a překračuje limity
Autor: Stanislav Mihulka (06.11.2024)
Ultralehká temná hmota by se mohla projevit v gravitačních vlnách
Autor: Stanislav Mihulka (23.10.2024)
Nový výzkum: Neutronové hvězdy by mohly být obklopeny mračnem axionů
Autor: Stanislav Mihulka (20.10.2024)
Primordiální černé díry se mohou skrývat na planetkách či měsících
Autor: Stanislav Mihulka (07.10.2024)
Diskuze:
Honza Dobrák,2013-12-20 12:34:02
Poissonova rovnice není omezena na 3D prostor, pouze je to nejběžnější případ.
Říkám, že známé fyzikální principy by nefungovaly, pokud bychom uvažovali jiné než 3 prostorové rozměry. Pokud byste chtěl mít více rozměrů, nemohl byste je považovat za rovnocenné s těmi 3 původními. Musel byste je nějak "znásilnit", aby vám nedělaly paseku v již známé fyzice. Takhle to dělají strunaři. Pak se ale já ptám, jestli to není jen hodně komplikovaná matematicko-fyzikální teorie, jejíž primární smysl je její neověřitelnost (vyšší dimenze jsou nám skryty).
Vojtech Kocian: stupne volnosti
Marek Pecina,2013-12-13 13:13:42
Člověče, pletete si stupně volnosti a rozměrnost prostoru. Jsou to dvě rozdílné věci které mají pramálo společného.
Z pohledu matematika to jedno
Vojtěch Kocián,2013-12-13 13:33:11
Ale především to byla ukázka pro pana Jičínského, že s vícerozměrným (matematickým) prostorem se pracuje naprosto běžně a nikdo se nenechá omezovat nějakou trojrozměrnou geometrií reálného světa, když více rozměrů potřebuje. Z matemamatického pohledu je problém více dimenzí prozkoumám velice dobře a kdyby nějaká vícerozměrná varianta lépe pasovala na reálný svět než ta klasická trojrozměrná, určitě by to nezůstalo bez odezvy.
A ano, ta ukázka se trochu zvrhla mimo téma, tak se omlouvám.
To Vojtěch Kocián
Petr Jíčínský,2013-12-13 15:46:23
Teď si úplně nejsem jistý, jestli vám rozumím. Pokud vím, tak teorie strun používá svinuté rozměry, takže těch jedenáct nebo kolik dimenzí nemají společný počátek. Já myslím něco jiného, totiž náhrada (x,y,z=4,8,12) za (k,l,x,y,z=1/5,8/3,9/5,10/12,5/8) přičemž Planckova konstanta v takovém systému by byla rovna jedné.
Petr Jíčínský,2013-12-12 10:10:15
No, kynutí těsta se dá ověřovat daleko lépe, než čtvrtý rozměr. Proč všichni známe jen 3 rozměry? Protože vám to od základní školy říkají a nic víc není schopen lidský intelekt vnímat. Ale můžete dokázat, že svět má 3 rozměry a ne více?
To, že se vám něco líbí vůbec neznamená, že vystihujete podstatu. Ano, vědec navrhl, jak teorii ověřit. Ovšem to, že se do toho nikdo nehrne je dost vypovídající.
Honza Dobrák,2013-12-12 14:03:07
Ve fyzice se slovo "dokázat" nepoužívá ve stejném smyslu jako v abstraktních vědách (matematika, logika). Ve skutečnosti se tím spíš myslí "ověřit". Takže dokázat ve fyzice nic nelze. To byste si musel sestavit vlastni vesmír s vámi zvolenými pravidly a pak byste mohl něco dokazovat. Nějak takhle to funguje ve matematice.
Pokud bych řekl, že svět má >3 prostorové dimenze, pak by se mě logicky někdo zeptal, proč je tedy nevnímáme. Ale kdo je vnímá? Vnímá gravitace nebo elektromagnetická interakce tyto vyšší dimenze? Pravděpodobně ne, protože pokud si vyřešíte Poissonovu rovnici v jiném než 3 rozměrném prostoru, dostanete úplně jiné fyzikální zákony, než které známe. Např. intenzita pole bodového náboje nebo hmotného bodu by neklesala s kvadrátem vzdálenosti. Planety nemohou mít stabilní oběžné dráhy, pokud gravitační zákon má jiný tvar než 1/r^2.
Pokud jste zvídavější, přečtěte si třeba tento článek:
http://arxiv.org/pdf/gr-qc/9702052.pdf
Petr Jíčínský,2013-12-12 20:28:03
Opět základ. Pokud si vytvoříte rovnice ve trojrozměrném prostoru, pak můžete říct, že v jinorozměrném by to nefungovalo. Ptám se na důvod, díky kterému je vesmír popsaný trojrozměrnou fyzikou. Byl-li by popsán čtyřrozměrně, pak pochopitelně nebude fungovat v trojrozměrném. Trojrozměrný svět je nejjednodušší možný - a také trochu zoufalý, protože má konstanty vyjádřeny příšernými čísly.
Rozumějte, pokud říkáte, že intenzita klesá se čtvercem vzdálenosti, pak je to čistý výplod trojrozměrné geometrie, pokud ale máte svět s jiným počtem rozměrů, tak tato věta neplatí.
Poissonovu rovnici přece není možné řešit v jiném, než 3D prostoru, protože je psána pro 3D prostor a je s ním nerozlučně spjata. Kdyby byla Poissonova pro 4D, pak by byl určitě problém přepsat ji pro 5D. Ale o přepsání nejde, jde o pozorování. A pokud vás učí vše viditelné zapsat do tří os, pak je těžké si nejen představit, ale ještě těžší vypočítat něco na pěti osách. Chápu, že se lidský intelekt brání více osám, ale to je asi tak jediný důvod, proč jsou jen tři. Všechny fyzikální zákony od počátku vědy jsou psány pro 3D prostor, aplikovat jejich formu na jiný počet rozměrů dost dobře nejde.
Od 3D k 6+D
Vojtěch Kocián,2013-12-12 22:11:38
To, že intenzita klesá se čtvercem vzdálenosti, není žádný trojrozměrný konstrukt, to je ověřitelný fakt (ověřitelný v jednom rozměru - vzdaluji se od bodového zdroje a měřím). Na to pak byla napasovaná ta "trojrozměrná" rovnice, která jednak dobře popisovala realitu a teprve potom byla v souladu s trojrozměrnou teorií. Jaderné síly se chovají jinak, takže je tu určitý prostor pro další dimenze.
Poissonova rovnice není definována pro trojrozměrný prostor, ale pro naprosto obecný. Stejně tak Euklidovská geometrie a další principy. To, že fyzika obvykle s vyššími rozměry nepočítá (i když teorie relativity počítá se čtyřmi, superstrunová teorie s ještě více), ještě neznamená, že matematika nebo informatika tyto rozměry nevyužije. V informatice jsou pro reálné problémy využívány klidně i dvanáctirozměrné prostory. V robotice má rozumný prostor obvykle šest dimenzí, ale může mít méně i mnohonásobně více. Záleží na složitosti stroje a způsobu jeho popisu (většinou se to rozkládá na menší celky). Matematice, která je v pozadí, je to úplně jedno. Jen se každá dimenze na vstupu a výstupu musí napasovat na něco z reálného světa, aby to nebyla jen matematická hříčka, ale užitečný kus programu.
pro Kocian 3D a 6D
Stanislav Kaštánek,2013-12-12 22:25:34
Pokud vím , tak roboty používají např. 6. stupňů volnosti, to je robotická ruka se může pohybovat jako bod s využitím 6 nezávislých os rotace. Tedy 6 os rotace v důvěrně známém 3 rozměrném prostoru třeba skladu. Na co bude robotu 6D prostor, kde( pokud by snad existoval) člověk nic nenajde. Robot i člověk potřebuje nahoru/dolu, doleva/doprava a dopředu/dozadu. Za totáče stačil "5D prostor" ( zpátky ani krok!).
Ad Stanislav Kaštánek:
Vojtěch Kocián,2013-12-13 07:53:03
Robotická ruka opravdu mívá 6 stupňů volnosti vzhledem k vnějšímu prostoru (může mít méně a nejen za totáče to může pro danou aplikaci stačit), ale můžeme mít spolupracujících rukou více a pak nám stupně volnosti a tím i matematické dimenze pro řešení narůstají. Nebo můžeme mít jen jednu ruku, ale s více klouby, než je pro zajištění šesti stupňů volnosti vzhledem k prostředí nezbytně třeba, ale aplikace je vyžaduje (například aby se mohla protáhnout do špatně přístupných míst). Zkuste si spočítat, kolik máte stupňů volnosti na Vaší ruce/paži. Pro jednoduchost můžeme vynechat prsty. U mé mi vychází 7.
Věda
Martin Plec,2013-12-11 10:09:48
Na rozdíl od té vymyšlenosti s entanglementem a červími dírami, kterou jsem nazval pseudovědou, http://osel.cz/index.php?clanek=7319, toto považuji za vědeckou hypotézu. Nejen že autor zveřejnil bláznivou domněnku, ale zároveň navrhnul i způsob, jak ji ověřit. To jen poznámka pro ty, co se mnou tehdy v diskuzi polemizovali.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce
