Měříme poloměr protonu
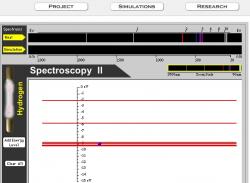
Abychom změřili něco tak malého, jako je poloměr protonu, potřebujeme ještě něco menšího, s čím to porovnáme. Ideální pro tuto službu je elektron, proto jedna z metod měření radiusu proton spočívá v ostřelování této částice elektrony a následné sledování rozptylu odrazů. Druhá metoda na to šla „od lesa“, sledováním energetických hladin protonu pomocí vodíkové spektroskopie. Je potřeba si uvědomit, že proton a elektron tvoří ten nejjednodušší prvek – vodík. Vědci po opakovaných pokusech dospěli k výše uvedenému závěru, tedy že poloměr protonu je 0,88 ± 0.01fm.
Potom přišli v roce 2010 s novou metodou, kdy zopakovali pokus se sledováním energetických hladin protonu, ale elektron nahradil jeho mnohem těžším příbuzným mionem (je 200 krát těžší než elektron). Ten díky své hmotnosti obíhá podstatně blíže protonu a vědci tak změřili poloměr protonu podstatně precizněji jako 0,842 ± 0,001 fm. Výsledek je mnohem přesnější, ale zcela se vymyká deklarované přesnosti předchozím pokusů. Od té doby vědci řešení záhadu poloměru protonu.
Roberto Onofrio z univerzity v italském Padově přišel s hypotézou, že daná nesrovnalost je projevem kvantové gravitace. Při tomto pokusu se měří tzv. Lambův posun. Ve své podstatě se jedná o pozorovaný rozdíl v energiích mezi 2S1/2 a 2P1/2 orbitaly. Podle Diracovy rovnice by měly mít tyto orbitaly stejnou energii, ale tato rovnice nepočítá s vlivem vakua na elektron a proto má 22S1/2 jinou energii. Onofrio tvrdí, že díky podstatně větší hmotnosti mionu je možné naměřit menší poloměr protonu, než je tomu u měření s elektronem, podle něj je příspěvek kvantové gravitace rozdílný o dva řády. Podle jeho výpočtů lze slabou interakci mezi nabitými částicemi považovat za projev kvantové gravitace, tedy gravitace na a pod Fermiho škálou. Podle něj je dané měření projevem unifikace slabé jaderné interakce a gravitace. Jeho tvrzení by mohlo být ověřeno pokusy, kdy by se měřil Lambův posun u deuteria nebo hélia. Tyto pokusy s exotickými atomy jsou sice nesnadné, ale jsou v možnostech našich současných technologií. Proto uvidíme, zda dojde k potvrzení nebo vyvrácení Onofriovy hypotézy a zda jsem skutečně konečně na stopě kvantové gravitaci.
Zdroje: Hydrogen Spoectroscopy http://phys.educ.ksu.edu/vqm/free/h2spec.html
Lamb shift http://en.wikipedia.org/wiki/Lamb_shift
http://phys.org/news/2013-11-proton-radius-puzzle-quantum-gravity.html
Diskuze:
Marek Šarmír,2013-11-29 19:57:56
Jednu vec som pozabudol. Akým spôsobom sa častice v atóme potom vlastne presúvajú?
Marek Šarmír,2013-11-29 19:57:56
Jednu vec som pozabudol. Akým spôsobom sa častice v atóme potom vlastne presúvajú?
Proč by nemohl mít proton jiný průměr?
Pavel Krajtl,2013-11-29 03:10:39
Jiný v koexistanci s elektronem a jiný s mionem.
není pro to žádný důvod
Pavel Brož,2013-11-29 08:47:26
Máte možná na mysli něco na způsob, jako když se vzdálenost mezi kvarky "zdrcne" či natáhne v závislosti na tom, zda je proton obíhán atomem či mionem? Jenže problém je v tom, že ty vzdálenosti mezi kvarky jsou určeny z více než 99 procent pouze silnou interakcí, nikoliv elektromagnetickou interakcí. Dále mion i elektron působí na proton, tedy na jeho kvarky prakticky výhradně elektromagnetickou silou, a ta je u obou stejná, mají totiž identický elektrický náboj. Jediný rozdíl, který vede i k jiným hodnotám Lambova posunu pro vodík a mezovodík jsou odlišné příspěvky k tomu, čemu se říká kvantová polarizace vakua, která je způsobena virtuálními páry částice-antičástice (v kvantové elektrodynamice jsou popisovány tzv. jednosmyčkovými Feynmanovými diagramy). Tyto příspěvky jsou pro mion a elektron výrazně odlišné právě pro jejich rozdílnou hmotnost (protože mion je zhruba dvěstěkrát těžší, než elektron), a proto hodnota Lambova posunu, což je právě efekt působený tou kvantovou polarizací vakua, je výrazně odlišná pro atom a mezoatom. Z hodnot Lambova posunu se pak dá zpětně usuzovat na velikost protonu. Tato velikost by teoreticky měla vyjít stejná bez ohledu na různé velikosti Lambova posunu.
Problém je v tom, že při výpočtu Lambova posunu se používá celá řada předpokladů, a ty nemusí být všechny splněny stejnou měrou pro elektron a mion. Rozdíl v řádu 7 procent není nijak dramatický, a je velmi pravděpodobné, že bude časem vysvětlen po započítání dosud přehlížených korekcí majících původ ve standardním modelu, nikoliv v kvantové gravitaci.
Marek Šarmír,2013-11-29 19:07:34
Mal by som dotaz, vlastne dva. Hoci majú mión a elektrón rovnaké náboje nemalo by sa uvažovať aj to, že mión obieha k jadru atómu bližšie ako elektrón a teda v mieste jadra pri mióne je väčšia intenzita pola ako je tomu pri elektróne? Hoci silná interakcia je ako ste písali výrazne silnejšia.
Druhý dotaz by sa týkal samotného vplyvu gravitácie na polomer jadra protónu. Ak samotná elektromagnetická interakcia pôsobí vzhladom na silnú jadrovú interakciu zanedbatelne, aký môže mať potom vplyv gravitácia, ktorá je už len oproti elektromagnetickej (nieto ešte silnej jadrovej) interakcii o mnoho rádov slabšia?
Pavel Brož,2013-11-29 19:36:27
takhle, děje, které se tam popisují, rozhodně nelze popsat ani pomocí klasické mechaniky, ani pomocí klasické teorie elmag. pole, dokonce ani pomocí kvantové mechaniky - adekvátní aparátem je až kvantová teorie pole, protože se tam počítá i s kvantovými fluktuacemi vakua (právě ty způsobují onu zmíněnou polarizaci vakua a tím i Lambův posun). Tak např. představa, že mion či elektron obíhají kolem jádra je sama o sobě nesprávná - řeč je o tzv. stavech atomu či meziatomu, konkrétně o stavech 2S1/2 a 2P1/2. Např. stav 2S1/2 je sféricky symetrický, tzn. že elektron či mion se v něm vyskytují s pravděpodobností, která je sféricky symetrickou funkcí polohy (bývá to v učebnicích chemie znázorňována jako takový sférický obláček). K žádnému oběhu zde nedochází, jedná se o tzv. stacionární stav - dá se říct v podstatě akorát to, že elektron či mion se s nějakou distribucí pravděpodobnosti vyskytuje v okolí jádra, nikoliv že obíhá.
Ve výpočtu Lambova posunu v mezovodíku jsou samozřejmě zohledněny i všechny elektromagnetické efekty plynoucí z toho, že mion "obíhá" (vyskytuje se) dvěstěkrát blíže, než elektron.
Co se týče vlivu gravitace, tak poměr její síly k síle elektromagnetické je zhruba 10^-39 pro vodík a 10^-37 pro mezovodík, tedy naprosto zanedbatelná.
Marek Šarmír,2013-11-29 19:54:16
Vdaka za objasnenie, určite si o tom ešte niečo zistím. Akým spôsobom by však potom mohla byť (hypoteticky) za rozdielne namerané hodnoty polomeru protónu zodpovedná kvantová gravitácia? Je nejaký rozdiel medzi gravitáciou prejavujúcou sa v makrosvete a kvantovou gravitáciou, prípadne sa nad nejakým rozdielom uvažuje?
ad kvantová gravitace
Pavel Brož,2013-11-29 22:27:20
Rozdíly mezi klasickou gravitací a kvantovou gravitací jsou, i když zatím ověřenou teorii kvantové gravitace nemáme a dlouho mít nebudeme. Kandidátů na teorii kvantové gravitace je více, jednak jsou to tzv. superstrunové teorie (resp. tzv. M-teorie, která by měla být zobecněním superstrunových teorií), potom dále tzv. smyčková teorie gravitace, ale i další. Nejvíce přívrženců má mezi teoretickými fyziky M-teorie, následují s velkým odstupem přívrženci smyčkové gravitace, no a ti zbylí už spíše paběrkují, dalo by se říci nezřídka je to autor té teorie sám, kdo tvoří její celý fanklub. Nicméně nikde není psáno, že pravdu musí mít ta teorie, která má nejvíce fandů.
Asi všechny kvantové teorie gravitace se shodnou na existenci gravitonů, tj. kvant gravitačního pole. Podobným způsobem se totiž od sebe liší kvantová elektrodynamika od klasické elektrodynamiky, v kvantové elektrodynamice totiž dostáváte kvanta elektromagnetického pole, tj. fotony. V klasické elektrodynamice žádná kvanta nedostanete, musíte je tam postulovat (poprvé tak učinil Planck, resp. obecněji Einstein, a položil tím začátek kvantové teorie). Je trošku paradoxní, že ačkoliv kvantová teorie odstartovala položením hypotézy existence kvant elektromagnetického pole - fotonů - tak se potom čtyři následující desetiletí vyvíjela jakožto kvantová mechanika, nikoliv kvantová teorie pole, do níž se vyvinula až po druhé světové válce.
Takže podobně, jako existují kvanta elektromagnetického pole, tak se předpokládají kvanta gravitačního pole - gravitony - v teorii kvantové gravitace.
Velikost kvantově gravitačních efektů, resp. rozměrové či energetické škály, na nichž by měly hrát roli, jsou velice diskutabilním tématem. Po dlouhá desetiletí se mělo za to, že kvantově gravitační efekty budou hrát roli až na tzv. Planckově škále, což je délka 10^20 krát menší než je rozměr protonu. V částicových experimentech platí princip nepřímé úměry mezi velikostí zkoumané délkové škály a velikostí energií srážejících se částic - tzn. že pokud chcete srážkami zkoumat desetkrát menší rozměry, musíte použít desetkrát větší energii. Tzn. že pokud se chcete dostat na Planckovu škálu, musely by mít srážející se částice řádově 10^16 krát větší energii než je maximálně projektovaná energie částic v LHC. A to je samozřejmě nemožné.
Na Planckově škále pak mělo docházet k fluktuacím samotného prostoru. Jak konkrétně by to mělo vypadat, to nikdo neví, spolehlivé teorie nejsou, předpokládalo se, že na této škále spontánně vznikají a zanikají mikroskopické černé díry, fluktuuje i topologie prostoru, atd.. Na škále velikosti nukleonů, tj. na škálách o dvacet řádů větších, už měl být prostor dokonale hladký, rozhodně nikdo neuvažoval o tom, že by se ještě na této škále mohly kvantově gravitační efekty nějak projevovat.
Změna přišla někdy v devadesátých letech, kdy podle některých verzí superstrunových teorií mohly kvantově gravitační efekty hrát roli už na podstatně větších délkových škálách, tedy i pro mnohem nižší energie. Dokonce se tehdy zrodila hypotéza, že mikroskopické černé díry možná vytvoříme už při energiích dosažitelných na LHC, pročež se tato možnost začala také okamžitě zkoumat. Tato otázka je samozřejmě stále otevřená, protože i když tyto černé díry nenajdete, tak vždy můžete tvrdit, že jsou už "za rohem", že se objeví při dalším malém zvýšení energie na urychlovači.
Mikroskopické černé díry, pokud budou na LHC objeveny, tak by se měly vzápětí vypařit za vzniku již známých standardních částic. Objevitelné by měly být podle podle specifického rozdělení druhů a energií těch sekundárních částic, nicméně spolehlivý průkaz tohoto jevu na pozadí miliónů jiných standardních rozpadů je vědou samou o sobě. Jinými slovy řečeno, i kdyby občas takovéto procesy na stávajícím LHC probíhaly, mohlo by trvat i měsíce až roky, než by byly v té záplavě dat spolehlivě rozpoznány. Ostatně příběh hledání Higgsova bozonu je velice podobný, nakonec se ukázalo, že jeho hmota je natolik nízká, že v urychlovačích vzácně vznikal už dost možná před deseti či více lety, nicméně na jeho spolehlivý průkaz to vyžadovalo posbírat dostatečnou statistiku, což ovšem zase bylo možné až při dalším zvýšení energií a po mnoha dalších optimalizacích.
Marek Šarmír,2013-11-30 11:35:37
Sú momentálne k dispozícii nejaké výpočty s akou pravdepodobnosťou môže vzniknúť mikroskopická čierna diera pri energiách dosiahnutelných súčasnými urýchlovačmi? Mimochodom vdaka za vyčerpávajúcu odpoved.
ad pravděpodobnost vzniku černé díry
Pavel Brož,2013-11-30 14:40:14
Jelikož nemáme jednu ověřenou teorii kvantové gravitace, ale místo toho máme mraky neověřených teorií kvantové gravitace, které se dramaticky liší v tom, na kterých energiích budou ty mikroskopické černé díry vznikat, tak tím pádem nějakou celkovou pravděpodobnost jejich vzniku spočíst nelze. Je to totéž, jako byste před rokem 2000 chtěl spočítat pravděpodobnost konce světa v roce 2000 na základě všech možných obskurních věšteb, kterýma se to v té době jenom rojilo. Z nepodložených předpokladů nemůžete chtít vypočíst pravděpodobnost.
Samozřejmě že většina z těch dílčích teorií tu pravděpodobnost nabízí, podle těch standardnějších teorií kvantové gravitace je ta pravděpodobnost při byť největších energiích LHC nulová, podle jiných už nenulová, byť malá.
Zajímavější a svého času hodně přetřásaná byla spíše otázka pravděpodobnosti, že mikroskopická černá díra, pokud vznikne, bude pak růst a spolkne naši planetu. Touto otázkou se opravdu nemálo vědců zabývalo, s výsledkem, že nic takového se v LHC nestane. Nemůžeme sice vyloučit, že v LHC mikroskopická černá díra vznikne, zato ale můžeme spolehlivě vyloučit scénář, že by pak rostla a spolkla Zemi. Asi nejpodstatnějším argumentem je existence Měsíce i ostatních planet sluneční soustavy. Ten je totiž bombardován z vesmíru těmi samými částicemi, které obíhají v LHC, a navíc dokonce i s energieme až o sedm řádů většími, tedy takovými, na které si tady na Zemi ještě hodně dlouho nesáhneme. Tzn. že pokud by těch srážkách mikroskopické černé díry vznikaly a pokud by měly dále růst místo aby se vypařily, tak by zde Měsíc už dávno nebyl.
Marek Šarmír,2013-11-30 15:48:04
Čo sa týkalo otázok pohltenia Zeme mikroskopickou čiernou dierou, tak ak sa dobre pamätám mal tu pán Wagner k danej problematike vynikajúci článok kde boli vysvetlené dané možnosti vzniku a dalšieho vývoja takýchto typov čiernych dier. Tam uvedené argumenty boli dosť presvedčivé a hlavne logické, aj ked je pravda, že v kvantovom svete nebeží všetko tak ako si predstavujeme. Skôr by bolo na dlhšiu a zaujímavejšu debatu baviť sa o spôsoboch vyparovania čiernych dier, ale nechcem to tu zbytočne naťahovať.
Radšej by som sa vyjadril ešte k tým pravdepodobnostiam, ktoré sú pre každú teóriu iné. Nie sú teda nijaké prepočty pri akých energiách sa musia zrážať častice tak, aby vznikla taká koncentrácia energie, kde bude gravitačná sila taká velká, aby vznikla mikroskopická čierna diera? Ked sa nad tým zamyslím, tak pokial budeme brať príklad z makrosveta, tak z gravitačného zákona sa dá vypočítať pri akej hustote hmoty vznikne čierna diera, t.j. pri určitom gravitačnom zrýchlení už svetlo z gravitačného pola takéhoto telesa uniknúť nemôže. Nedalo by sa to spočítať aj pre mikroskopické čierne diery? Predpokladám, že pri zrážkach častíc treba brať do úvahy aj ich hybnosť v čase zrážky, čo u makroskopických objektov asi nie je potrebné.
ad energie nutná pro vznik černé díry
Pavel Brož,2013-11-30 18:41:49
Takhle, z hlediska nekvantové teorie je proces vznik černých děr velice detailně popsán. V principu, když to hodně zjednoduším, vznikne černá díra (za splnění jistých předpokladů) pokaždé, když uvnitř dostatečně malého objemu soustředíte dostatečně hodně hmotnosti či energie (vzhledem k rovnici E=mc^2 je to ekvivalentní; mimochodem, hybnost hmoty je zde automaticky započítána, protože s růstem hybnosti roste i ona dynamická hmotnost m). V rámci nekvantové teorie byly spočítány např. i tak exotické procesy, jako vznik černé díry koncentrickým laserovým pulsem. Ty předpoklady, které musí být splněny, souvisí s nábojem a momentem hybnosti („rotací“) černé díry či hmoty, z níž by černá díra měla vzniknout. Ukazuje se totiž, že pokud má kolabující hmota extrémně velký náboj či extrémně velký moment hybnosti vzhledem k její hmotnosti, pak klasická černá díra s horizontem událostí nemůže vzniknout, může vzniknout maximálně tzv. nahá singularita, která nemá žádný horizont, a je to opravdu jen bodová singularita, tj. nemá žádný definovatelný objem.
Velikost černé díry vzniklé kolapsem hmoty se dá spočíst z velikosti energie vtěsnané pod objem odpovídající jejímu horizontu, a naopak, pokud chcete vyrobit černou díru nějaké velikosti, můžete zpětně dopočítat množství energie, které k tomu budete potřebovat. Takže dejme tomu chcete vyrobit černou díru velikosti protonu, tj. o průměru řádově 10^-15 metrů. K tomu budete potřebovat soustředit do objemu protonu hmotnost o velikosti řádově 10^12 kg (tedy miliardu tun, čiliž hmotnost jednoho krychlového kilometry vody). Je samozřejmě jasné, že něco takového je naprosto nereálné.
Mohl byste samozřejmě slevit z velikosti požadované černé díry, aby dodaná energie byla v mezích, jaké jsme schopni dosáhnout na současných urychlovačích. Tak např. maximální projektovaná energie LHC je 14 TeV, což je ekvivalent hmotnosti zhruba 2,5*10^-23 kg. Odpovídající černá díra by měla průměr řádově 10^-50 metrů. Pod objem o tomto průměru byste musel soustředit veškerou energii dvou srážejících se částic v LHC, abyste takovou černou díru vytvořil.
Jenže zatím jsme se pohybovali na půdě nekvantové teorie, která předpokládá nekonečně dělitelný a hladký prostor na libovolně malých škálách. Jakmile ale chceme začít uvažovat též kvantové jevy, tak se ukazuje, že tento přístup není možný, protože od určité prostorové vzdálenosti níže budou už kvantové fluktuace tak silné, že bude díky virtuálně vznikajícím a zanikajícím částicím docházet ke spontánnímu vzniku a zániku černých děr, a že prostor na takto malých škálách bude připomínat spíše vodní tříšť než hladkou hladinu. Velikost této škály, pod kterou už nemá smysl uvažovat o prostoru jakožto dále dělitelném hladkém kontinuu, je dána tzv. Planckovou délkou, ta činí řádově 10^-34 metrů. Protože v rámci kvantové teorie gravitace se nemá smysl bavit o menších škálách, tak nejmenší černou děrou, která může vzniknout (ba která dokonce vzniká a zaniká spontánně bez jakéhokoliv našeho přičinění čistě jen v důsledku kvantových fluktuací), je černá díra Planckovy velikosti. Abychom takovou mohli v LHC vyrobit, potřebovali bychom jednak 10^16 krát více energie, než je oněch 14 TeV, a jednak umět tu energii soustředit v oblasti o velikost Planckovy délky. Obojí je naprosté sci-fi.
Jak už jsem dříve zmínil, po několik desetiletí se věřilo, že kvantově gravitační efekty, včetně např. možného vzniku černých děr v urychlovačích, budou doménou pouze té Planckovy škály, tj. že po několik nejbližších století si s nimi nebudeme muset lámat hlavu, protože na jejich experimentální ověřování prostě nebudeme mít dost energie. Zhruba v devadesátých letech se ale začaly objevovat varianty superstrunových teorií, které připouštějí vznik mikroskopických černých děr už při dnes dosahovaných energiích. Dlužno říct, že variant superstrunových teorií je jako máku, přičemž jejich předpovědi se mezi sebou diametrálně liší. Všechny superstrunové teorie pracují s tím, že skutečný počet dimenzí našeho prostoru není tři dimenze, ale devět či deset dimenzí, přičemž různé varianty se těch nadbytečných rozměrů zbavují různě. Některé varianty superstrunových teorií ty nadbytečné dimenze „balí“ do jakýchsi mikroskopických šestidimenzionálních „kuliček“ (těm se říká Calabi-Yauovy variety, a ve skutečnosti nemají kulový, ale extrémně složitý tvar, výraz kulička jsem použil proto, že se jedná o do sebe uzavřené prostory, podobně, jako je do sebe uzavřená např. kulová plocha či povrch pneumatiky). Jiné varianty superstrunových teorií hlásají, že v nějakém mnohem větším superprostoru se vznáší třírozměrné tzv. „brány“, přičemž jedna z nekonečně mnoha takových brán tvoří náš třírozměrný vesmír. Každopádně podobných variant superstrunových teorií je mnoho a jejich předpovědi se od sebe diametrálně liší.
No a právě podle některých z těchto superstrunových variant by mikroskopické černé díry mohly vznikat, byť extrémně vzácně, už při současných energiích. Pokud ty černé díry budou skutečně v LHC objeveny, budou fanynky a fanynci těchto teorií na koni, a budou se pyšnit tím, že jimi vyznávaná teorie měla pravdu. Pokud ty černé díry objeveny nebudou, budou tytéž fanynky a fanynci říkat, že je potřeba ještě více voroštovat to LHC a pak že už to bude.
Ať tak nebo tak, rozhodně se tyto jevy nedají počítat aparátem klasické teorie. A aparátem jaké že teorie se teda mají počítat? No to už záleží, čí teorie jste fanda. Jestli zastáváte tezi, že žijeme na jedné z nekonečně mnoha trojrozměrných vesmírů vznášejících se v devíti či desetirozměrném nadvesmíru. Anebo jestli zastáváte tezi, že žijeme v devíti či desetirozměrném vesmíru, ale ty nadbytečné dimenze jsou sbaleny do těch rafinovaných Calabi-Yaouvých variet (pak také bude záležet na tom, na jaké rozměrové škále podle vás k tomu balení dochází, protože právě to podstatně ovlivňuje ty energie, při kterých by se ty mikroskopické černé díry daly už vytvářet). Anebo jestli jste nepřítelem všech verzí superstrunových teorií a zastáváte teorii smyčkové gravitace. Pokud jste někdy viděl seriál Teorie Velkého třesku, tak zajisté chápete, že mezi přívrženci těchto rozdílných táborů plane nesmiřitelný boj :-)
Marek Šarmír,2013-11-30 22:58:35
Nie som fanúšikom žiadnej teórie, pretože žiadnu neovládam dostatočne dobre nato, aby som si mohol povedať, že táto sa mi pozdáva najviac. Každopádne patrí vám moje velké podakovanie, že ste boli ochotný obetovať svoj čas, aby ste odpovedali na moje otázky. Verím, že ešte spolu budeme diskutovať pri iných témach.
Majú zmysel merania polomeru v protónov a podobne
Anton Matejov,2013-11-28 10:44:20
V poslednom čase som prišiel k domnienke, že niektoré kvantové javy môžu spôsobovať gravitáciu nepriamo.
Úvaha:
1.) rozmerom rovnaké telesa s väčšou hustotou majú vyššiu gravitáciu.
2.)Hustejšie telesa majú viac kvantových javov na jednotku rozmeru.
3.)Niektoré kvantové javy,(slabé interakcie uvoľňujú väzby v ktorých je kumulované množstvo energie. Iné kvantové javy (silne a elektromagnetické)zasa zapríčiňujú,alebo udržujú väzby kde sa uskladňuje energia vo väzbách. Čo ak viac niektorých častých a bežných kvantových javov na jednotke priestoru, vychyľuje nepomer medzi kvantovými silami spôsobujúce väzby na kvantových úrovniach oproti silám, čo zapríčiňujú rozpad väzieb?
Vychýlenie tejto rovnováhy väzobných v neprospech sil rozvezujúcich väzby na kvantovej úrovni zapríčiňuje gravitáciu.
Čím je takéto teleso hustejšie na jednotku, tým zasa narastá nepomer týchto akcii a prejavuje sa to v makrosvete.
ad počet kvantových jevů na jednotku objemu
Pavel Brož,2013-11-28 21:36:19
Hustota kvantových jevů má asi takový smysl, jako třeba hustota Newtonovských jevů či hustota kulinářských jevů. Resp. vždycky můžete najít tři tucty obskurních způsobů, jak takováta a podobná čísla definovat, ale smysl to nemá pražádný. Pokud jste někdy obědval ve školní jídelně i ve špičkové restauraci, tak na totéž přijdete sám. Dokonce by se dalo říct, že ty kulinářské jevy mají k těm gravitačním mnohem větší korelace, než ty kvantové.
Pár poznámek
Vladimír Wagner,2013-11-27 23:30:56
Česky se nepíše muon ale mion. Hlavní problém článku však je, že následuje všeobecnou tendenci ze všeho vytvořit senzaci. Věta "Pak přišel další tým s jinou metodou, která toto měření postavila na hlavu." absolutně neodpovídá situaci. Od nově naměřené hodnoty se ta, získaná evaluací hodnot z měření elektronového rozptylu na protonech a přechodů v atomu vodíku, liší o pět standardních odchylek. To je sice více než tři standardní odchylky, ale přesto ještě poměrně nepříliš významný rozdíl. Navíc není vyloučené podcenění některých systematických nejistot různých měření a jejich analýzy. A tedy, než bude možné reálně něco z rozdílu dedukovat, je potřeba udělat podrobný rozbor právě různých vlivů, které mohou způsobit vznik systematických nejistot. A přesně na to třeba upozorňují experimentátoři na domovských stránkách skupiny, které měření mionového vodíku provádí.
Možná, že takový senzacechtivý způsob psaní populárně vědních článků přiláká hodně čtenářů, ale vytváří velice mylný dojem o vědě i vědecké práci. Zvláště, když výsledek vznikl tichou poštou průchodem přes několik populárně vědních serverů a každý další autor přidal expresivnější výrazivo, aby senzaci ještě více zvětšil. Pochopitelně není vyloučeno, že rozdíl je reálný a něco zajímavého přinese, ale s největší pravděpodobností se po náročné analýze podaří odhalit a snížit nejistoty v měřeních různými metodami a ty se nakonec sejdou. Zpřesní se tak znalost jedné ze základních konstant, což je velmi důležité, ale senzace zmizí. Věda je opravdu hlavně založena na mravenčí práci a zpřesňování. Které teprve postupně může přinést zlom či třeba i senzaci. Ale opravdu jen výjimečně. Články, jako tento vytváří dojem, že senzace jsou neustále a neustále se vzájemně popírají a vyvracejí. Což je ale opravdu nerealistický obraz toho, co se ve vědě děje.
Kvantová gravitace je hypotéza (ani ne příliš dobudovaná), která zatím nestojí na žádném experimentálním faktu a to, že by její prokázání mohlo být postaveno na tomto rozdílu měření poloměru protonů (vysvětlitelném řadou klasičtějších efektů), není moc reálné.
Trochu mi to připomíná diskuze, které se vedly okolo možnosti, že jsou neutrina tachyony, založené v devadesátých letech na pozorování anomálie ve spektru elektronů z rozpadu tricia (http://hp.ujf.cas.cz/~wagner/popclan/neutrina/neutrina.html ), nebo nedávno při měření rychlosti neutrin experimentem OPERA (http://www.osel.cz/index.php?clanek=5896 ).
Pokud se článek týká rozměru protonu nebo nadsvětelné rychlosti neutrin, tak senzační článek nemá v principu negativní dopad. Horší je, když se podobný způsob psaní použije v článcích, které se týkají různých rizik. Pak je každé, byť statisticky zanedbatelné zvýšení rizika smrtelné, každá dávka smrtící a koncentrace vražedná.
Souhlasím
Pavel Brož,2013-11-28 00:21:45
Čekal jsem, že toto téma okomentujete, jelikož je z Vašeho fochu. Myslím si totéž co Vy, totiž že výsledkem bude maximálně zpřesnění některých parametrů toho modelu, podle nějž se to počítá, možná dokonce se zjistí, že v případě mionů není možné provádět určitá zjednodušení, která se při výpočtu dělají s elektrony, a že teprve po započtení dříve zanedbávaných efektů nastane shoda. Tento scénář není nijak senzační, zato se v experimentální fyzice, zvláště pak ve fyzice elementárních částic, opakuje velice často. Takže si stejně jako Vy myslím, že na nějaké úvahy o kvantově-gravitačních efektech je pořád ještě fůra času.
Mimochodem, nedalo mi to, a otevřel jsem si ten Lambův posun, na kterém je ten pozorovaný fenomén založen, ve stařičké učebnici kvantové elektrodynamiky od Beresteckého, Lifšice a Pitaevského. Lambův posun je tam vypočítán obecně, nejen pro rozdíl hladin 2S1/2 a 2P1/2. Je tam diskutován i případ Lambova posunu v mezoatomech (přesnější by bylo asi napsat v mezovodíku podobných mezoiontech), tj. atomech s elektronem substituovaným mionem, tedy přesně to, co se nyní měřilo. Je to vydání z roku 1989, v té době to byla spíše akademická záležitost. Každopádně výpočet Lambova posunu, ačkoliv byl prvně proveden v nerelativistickém přiblížení už v roce 1947 Bethem, přesněji pak Krollem a Lambem v roce 1949, není vůbec jednoduchý („výpočet“, který je uvedený na wikipedii odkazované pod článkem, opravdu být použit nemůže), a používá se při něm celá řada předpokladů. Lze si snadno představit, že některý z těchto předpokladů, ač platí dostatečně přesně pro elektron, neplatí už s takovou přesností pro mion, a přesně toto bych čekal, že se časem objeví jako vysvětlení ono záhadného (a velikostí nijak dramatického) rozdílu. I bez použití kvantové gravitace.
Smysl rozměru
Leopold Kyslinger,2013-11-27 15:07:43
Domnívám se, že smysl ptát se po poloměru, je korektní, Protože jestliže hadronům přisuzujeme duální charakter (vlnový a korpuskulární), tak má také smysl posuzovat jejich chování jako jako chování částice o rozměrech...atd. Tím rozměrem není hadron určen - je to jenom projev.
otázka
Stefan Urge,2013-11-27 14:31:48
Ja by so sa spýtal, ako je vlastne definovaný polomer častice, či protónu. Je zrejmé že nie je "gulička". Ale ako si to meranie mám potom predstaviť, veď zrejme nemá pevnú hranicu - ohraničenie. Pri inakšom meraní dostanem iný výsledok, ťažšia častica (müon) sa bude chovať inak v silovom poli ktoré tvorí asi hranicu atď.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce