V tomto týdnu probíhá konference i na Matematicko fyzikální fakultě University Karlovy v Praze. Jde o každoroční konferenci SPIN, která se také věnuje novým výsledkům v oblasti částicové fyziky. Zejména zkoumání podstaty spinu částic, což je specifická kvantová vlastnost (blíže viz zde). V jejím prvním dni, v pondělí, se uskutečnila série přednášek věnovaných výsledkům jednotlivých experimentů pracujících na urychlovači LHC. Ovšem přednášející nesměli ani naznačovat výsledky, které se měly prezentovat na dnešním očekávaném semináři v laboratoři CERN. I to svědčí o tom, jak media ovlivňují nejen celou společnost, ale i vědeckou komunitu, ale také o tom, že informace se dnes šíří opravdu přímo rychlostí světla, často i doslovně. Určitý náznak, jaké budou ty prezentované výsledky, nabízí fakt, že v průběhu letošního dubna až června se podařilo získat větší statistiku dat než za celý minulý rok provozu. Další indicií bylo, že všechny zveřejněné výsledky velmi přesně potvrzovaly předpovědi standardního modelu hmoty a interakcí. Naopak se nepotvrzují jisté náznaky existence nové fyziky za standardním modelem, které se objevily v datech získaných experimenty na urychlovači Tevatron, jehož provoz byl nedávno ukončen. Nepozorují se zatím žádné známky nových částic nebo jevů, jež by podporovaly nějaké nové teorie za standardním modelem.
Koncem roku 2011 se v získaných datech experimentů ATLAS a CMS podařilo pozorovat náznaky existence higgsova bosonu v oblasti klidové energie okolo 126 GeV (viz zde). To je hmotnost zhruba 133krát větší než hmotnost protonu. Podobné náznaky se objevují i při pečlivé analýze dat, které získal urychlovač Tevatron (viz zde). Naznačovanou hmotnost higgse potvrzují i nepřímé indicie založené na velmi přesném určení hmotnosti bosonu W získané z dat obou experimentů, které na urychlovači Tevatron pracovaly (viz zde). A právě ověření těchto náznaků bylo letošním hlavním úkolem fyziků zmíněných dvou experimentů na LHC. O tom jak LHC a jeho experimenty vypadají (viz zde).
Proč je tak důležitá statistika
Nové částice, které experimenty na urychlovači LHC hledají a z nichž nejznámější je higgs, žijí jen velice krátce a rychle se rozpadají na jiné. Některé z těchto sekundárních produktů se ještě před tím, než stihnou doletět k detektorům, rozpadnou také. Fyzikové se proto zaměřují na identifikaci příslušných skupin částic produkovaných v rozpadu hledané nové částice, například higgse. Pokud jim jejich detektory pomohou správně zachycené částice určit a stanovit jejich energii a hybnost, lze na základě zákona zachování energie a hybnosti určit hmotnost původní částice, z rozpadu které sekundární částice pocházejí. Problémem je, že příslušné kombinace částic mohou vznikat i v rozpadech jiných částic a v jiných procesech. Vytváří se tak pozadí, na kterém je třeba příspěvek z rozpadů higgsů hledat. Pro danou hmotnost vypočítanou ze zachycených sekundárních částic je možné na základě standardního modelu předpovědět pravděpodobnost vzniku různých částic (tedy i hledaného higgse) a jejich různých rozpadů. To umožňuje posoudit, jak pozorování těmto předpovědím příspěvků pozadí i existence higgse odpovídá. Problém je, že pro rozeznání vlivu higgse a prokázání přebytku případů charakteristických pro danou hmotnost nad pozadím, nebo naopak pro vyloučení možné existence higgse, potřebujeme získat dostatečnou statistiku hledaných případů a tím i dostatečný počet srážek protonů. Produkce higgse má extrémně malou pravděpodobnost, a tak musí být počet srážek, jež mohou vést k jeho vzniku, extrémně velký.
Proč je Higgsův boson pro fyziky tak významný?
Ve standardním modelu je v části, která popisuje společně elektromagnetickou a slabou interakci, obsažen proces generující hmotnost u tří ze čtyř částic zprostředkujících tyto interakce. Jedinou částicí s nulovou klidovou hmotností, je dobře známý foton zprostředkující elektromagnetickou interakci. Třem zbylým – dvěma nabitým bosonům W+ a W- a neutrálnímu Z0 - hmotnost extrémně narostla až na přibližně devadesáti násobek hmotnosti protonu. Díky tomu je slabá interakce, kterou tato trojice bosonů zprostředkuje, extrémně slabá a má extrémně malý dosah. Higgsův mechanismus navržený skotským fyzikem Peterem Higgsem, který takové generování hmotnosti u částic popisuje, zároveň předpovídá existenci částice označované podle autora teorie jako Higgsův boson nebo prostě „higgs“. Je třeba zdůraznit, že Higgsův mechanismus vysvětluje generování hmotnosti ve světě částic jen z části. K vysvětlení hmotnosti v jiných případech je potřeba mít jiné mechanismy.
Higgsův mechanismus je nezbytnou součástí standardního modelu a higgs je tak poslední chybějící částicí tohoto modelu. Je tak přirozené, že pro fyziky je prokázání jeho existence veledůležitým cílem. Jeho neexistence by znamenala, že Higgsův mechanismus musí nahradit něco jiného, což by však už do standardního modelu nepatřilo a vedlo by nás přímo do nové fyziky.
Standardní model nepředpovídá hmotnost higgse, jen ji omezuje shora. Pokud ovšem předpokládáme danou hodnotu hmotnosti, dokáže standardní model předpovídat pravděpodobnost jeho vzniku při srážkách protonů s danou energii a pravděpodobnost rozpadu na danou kombinaci sekundárních částic. A ty se pak, jak bylo zmíněno, hledají v naměřených datech.
Výsledky pozorování
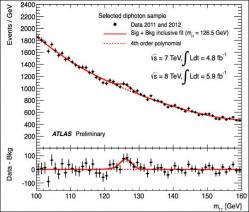
Nové výsledky experimentu CMS prezentoval Joe Incandela a za experiment ATLAS vystoupila Fabiolla Gianotti. V obou experimentech se při analýze nově získaných dat fyzikové soustředili na dva typy rozpadů. Stejné, ve kterých se náznaky higgse u energie 125 GeV objevily už při analýze dat z minulého roku. Prvním je rozpad na dva fotony gama s velmi vysokou energií. Druhým pak rozpad higgse na dva bosony Z. V tomto případě je třeba připomenout, že jeden z těchto Z musí být virtuální, protože klidová hmotnost dvou Z bosonů je větší než 125 GeV/c2. Oba Z bosony se mohou rozpadat na dva leptonové páry (buď mionů, nebo elektronu a pozitronu). A u tohoto typu rozpadu je pozadí velmi malé.
Analýza nových dat potvrdila přebytek případů pro uvedenou energii u obou experimentů a tím výrazně narostla pravděpodobnost, že se jedná opravdu o důkaz existence nové částice, jejíž vlastnosti jsou v souladu s tím, co pro klasického higgse předpovídá standardní model. Z pozorovaných rozpadů je jasné, že se jedná o boson. Jestli jde opravdu o standardního higgse, bude jasné až po podrobnější analýze pravděpodobností různých rozpadů i ve více kanálech rozpadu než jsou ty zde zmíněné dva.
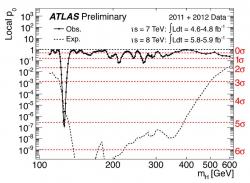
Experiment CMS tak deklaruje, že pozoruje silného kandidáta na higgse s hmotností 125,5 GeV s nejistotou 0,6 GeV. Pozorování je na úrovni 4,9 sigma, což znamená, že pravděpodobnost, že zjištěný přebytek je projevem jen statistické fluktuace pozadí, je pouze miliontina. U experimentu ATLAS je určená hmotnost 126,5 GeV a pravděpodobnost, že přebytek nelze vysvětlit fluktuací statistiky, je také na úrovní pěti sigma.
Závěr
I prezentace posledních dat dvou experimentů CMS a ATLAS, které k hledání higgsova bosonu využívají srážky protonů na urychlovači LHC, naznačují, že pravděpodobnost existence nové částice s hmotností zhruba 126 GeV je velmi vysoká. Tato částice je bosonem a má vlastnosti odpovídající v rámci nejistot standardnímu higgsi. Zároveň byl higgs s jinou hmotností nezvratně vyloučen. Je teď téměř jisté, že pokud opravdu je pozorovaný přebytek se standardním higgsem spojen, bude jeho existence do konce roku nezvratně prokázána. Do té doby totiž bude možno z analýzy řady různých reakcí zjistit, zda jejich pravděpodobnosti vlastnostem standardního higgse odpovídají. Takový výsledek je obrovským vítězstvím standardního modelu. Stejně jako jeho potvrzování zmiňované na začátku článku. Na jedné straně je to fantastické. Na druhé straně i trochu frustrující, protože se nám do jisté míry vzdalují možnosti spatřit signály nové fyziky za tímto modelem. LHC je ale teprve na začátku dlouhé, velmi plodné dráhy a určitě se můžeme těšit na další objevy. Některé z těch exotických, které se před spuštěním LHC diskutovaly, jsou zmíněny v článku Ohrožuje spuštění LHC naši existenci?
Diskuze:
Aktualita
Vladimír Wagner,2012-07-14 16:31:11
Vedení laboratoře CERN rozhodlo prodloužit letošní srážení protonů na urychlovači LHC o dva měsíce až do 18 prosince. Srážení těžkých jader s protony bude po vánoční přestávce v lednu a únoru a teprve pak začne dlouhá přestávka, která umožní přejít na vyšší energii protonů. To umožní získat vyšší statistiku důležitou hlavně pro zkoumání nových jevů a higgse. Nový přehled výsledků týkajících se higgse bude prezentován před Vánocemi.
Maroš Štulajter,2012-07-10 13:53:19
Musím sa pridať k ostatným diskutujúcim ktorý ďakujú za obsah diskusie p. Brožovi a p. Wagnerovi, ktorá výborne dopĺňa článok. ja som dostal zrozumiteľné odpovede na všetky moje dotazy v príspevkoch.
Peter Peter,2012-07-10 10:18:45
V prvom rade dakujem za komentar ktory mi aspon z casti objasnil moju otazku(Hmotnost castic?) v diskusii nizsie. Mozno by to este chcelo trosku viac popisat nasledovnu pasaz "U hmotnosti druhého druhu s jistotou víme, že je generovaná sekundárním efektem souvisejícím s tzv. chirální symetrií, přesněji s jejím narušením. ", ale inak nemam vyhrady.
Skoda ze Vasa reakcia nie je publikovana ako plnohodnotny clanok, pretoze mnoho citatelov diskusie necita. Vase reakcie v diskusiach su totizto bezpochyb prinosom.
Drzim palce a pridavam +1, "Like", plny pocet hviezdiciek a pod. :)
Hmotnosti hadronů a efektivní hmotnosti kvarků
Vladimír Wagner,2012-07-10 11:32:36
Jak už Pavel Brož psal, je hmotnost hadronů, zvláště těch složených z lehkých kvarků u, d a s, dána hlavně vlastnostmi silné interakce a procesu uvěznění kvarků při nízkých energiích (vlastnostmi vakua silných interakcí). Takž, jestliže je "první typ" hmotnosti kvarků u a d zhruba okolo 5 MeV a hmotnost protonu je okolo 930 MeV, tak je vidět, že opravdu je zhruba 95 % hmotnosti dáno právě tou hmotností "druhého typu" a tedy vlastnostmi uvěznění. Jinak kvarkový model hadronů pracuje s "efektivními" hmotnostmi kvarků, které zahrnují oba typy hmotností a umožňují přibližné předpovědi hmotnosti jednotlivých hadronů. Pojem efektivní hmotnosti je dobře znám i z jiných oblastí fyziky, zahrnuje vliv interakce částice.
Pokud se podíváme na hmotnosti hadronů, které obsahují kvarky c a b (jejich hmotnost prvního typu je 1,5 a 4,7 GeV/c2) tak tam už je velký podíl hmotnosti hadronu tvořen hmotností prvního typu.
Dovolil bych si jen menší opravu povídání Pavla Brože v této oblasti. Kvarky jsou uvězněny v hadronech, tedy za normálních podmínek v nukleonech. Takže bych spíše nemluvil o podmínkách v atomových jádrech ale podmínkách v hadronech (nukleonech), ve kterých jsou valenční kvarky silnou interakcí uvězněny.
je to tak, děkuji za opravu :-)
Pavel Brož,2012-07-10 22:18:16
ano, mělo být napsáno v nukleonech. Cítím se trošku nepatřičně, protože jsem se rozepsal o věcech, ve kterých jsem nikdy nebyl silný v kramflecích a které jsou Vaší doménou. Ostatně, nemálo informací jsem svého času získal právě z Vašich článků, které jste před lety uveřejnil mj. na Neviditelném psu, můžete prosím dát na ně odkazy? Nemálo zdejších čtenářů si je určitě rádo přečte, mě osobně se velice líbily.
Starší články
Vladimír Wagner,2012-07-12 11:39:34
Ty moje starší články jsou všechny pohromadě na http://ojs.ujf.cas.cz/~wagner/popclan/ . Ani já nejsem expert na teorie popisující strukturu hmoty a navíc při popularizaci se člověk dopouští řady zjednodušení, která nemusí být košer. Takže je vždy třeba brát takové texty hodně s rezervou a nadhledem. Něco jiného je populární přiblížení daného problému a reálné jeho pochopení a schopnosti něco spočítat a předpovědět.
ad problém hmotnosti
Pavel Brož,2012-07-10 02:15:50
Zvažoval jsem, jestli se nepokusím přiblížit ten problém hmotnosti více, ale vždycky zde existuje dilema mezi pochopitelností a nutným zkreslením toho přiblížení. Bohužel jsem přesvědčen, že zrovna tento problém nelze laicky vysvětlit tak, aby byl zároveň pochopitelný, a zároveň nebyl příliš zkreslující, přesto se o něco maličko nyní pokusím, sám s tímto svým pokusem ale nejsem příliš spokojen...
Problém hmotnosti je mnohovrstevnatý, protože na něm participuje více efektů. Také je důležité vědět, o jakém typu hmotnosti se bavíme. Tak např. u kvarků a gluonů je možno definovat hmotnosti dvě – jedna hmotnost koresponduje s kvarky a gluony v režimu asymptotické hmotnosti (v režimu extrémně vysokých energií, kdy se tyto částice v subnukleárních škálách rozptylují skoro jako volné). Druhá hmotnost koresponduje v režimu velice vzdáleném od podmínek asymptotické volnosti, je to režim, kdy kvarky a gluony mají relativně nízké energie (takové, jaké zhruba panují v obyčejných atomových jádrech, tj. ne např. v jádrech ostřelovaných vysokoenergetickými částicemi v těch nejvýkonnějších světových urychlovačích). Zatímco u prvého druhu hmotnosti mají např. kvarky u a d hmotnost několika málo elektronů a gluony jsou dokonce nehmotné, tak hmotnost druhého druhu je nejméně dvacetkrát větší. U hmotnosti prvého druhu nemáme pochyby o tom, že je generovaná Higgsovým polem (možná ne celá, zatím ale neexistuje jediný experimentální důvod, proč by nemohla být). U hmotnosti druhého druhu s jistotou víme, že je generovaná sekundárním efektem souvisejícím s tzv. chirální symetrií, přesněji s jejím narušením. Hmotnost druhého druhu se týká pouze částic interagujících silnou interakcí, tj. kvarků a gluonů. Protože elektrony neinteragují prostřednictvím silné interakce, ponechávají si pouze svou hmotnost „prvého druhu“, a proto v konečném důsledku zůstávají nepoměrně lehčí, než jsou nukleony, které sestávají jednak z trojice tzv. valenčních kvarků („ztloustnutých“ efektem generování hmotnosti „druhého druhu“), dále z tzv. mořských kvarků, a dále pak gluonů.
S použitím těch nejvýkonnějších superpočítačů na světě lze tuto druhou hmotnost s jistou chybou vypočíst, pokud se do výpočtu zadají jako parametry experimentálně známé hmotnosti několika baryonů (vypočtou se pak samozřejmě hmotnosti zbylých baryonů, kterých jsou ale stále desítky, takže tato metoda použitím hrubé výpočetní síly je testovatelná na souhlas s experimentem). V současné době neexistuje žádná matematická metoda, která by dokázala tyto hmotnosti pro ostatní baryony vypočíst, aniž bychom museli použít tu nejbrutálnější výpočetní sílu těch nejvýkonnějších strojů, které po mnohahodinovém, někdy i mnohadenním výpočtu vyplivnou nějaká data, která mohou být následně porovnána s experimentálními. Takováto matematická „nebrutální“ metoda se neúspěšně hledá už skoro půl století, nicméně přes mnohé nepochybné pokroky na poli matematiky jsme dnes co se týče tohoto problému „hmotnosti druhého druhu“ stále ještě odkázáni pouze na ty superpočítače.
Hmotnost prvého druhu je matematicky mnohem lépe uchopitelná, a k popisu Higgsova mechanismu, který generuje hmotnosti částic („hmotnosti prvého druhu“), není potřeba žádných superpočítačů, stačí tužka, papír a solidní matematické vzdělání (a teoreticko-fyzikální, samozřejmě). Přesto Higgsův mechanismus tyto hmotnosti neumí spočíst, protože ve hře je mnohem více parametrů. V každé teorii figurují minimálně dva základní parametry, kterými jsou vazebná konstanta a hmotnost (a to hmotnost prvého druhu, která je fundamentálnější, oproti tomu hmotnost druhého druhu může figurovat pouze v tzv. efektivních teoriích, které nejsou teoriemi popisujícími elementární částice, ale až složitější systémy, jako jsou různé vázané systémy, kondenzáty, atd. atd.). Přesněji řečeno, máme-li teorii popisující jeden jediný druh částic, máme zde minimálně dvě konstanty, hmotnost a vazební konstantu. Vazebních konstant může být i pro tuto jednoduchou teorii popisující jen jeden druh částic ve skutečnosti více, záleží na množství členů v interakční části. Nicméně s počtem částic maximální možný počet různých vazebních konstant rychle narůstá. Tak např. pro kubickou interakci tří polí A, B a C může být u kteréhokoliv z následujících členů separátní vazebná konstanta: AAA, AAB, ABB, BBB, AAC, ABC, BBC, ACC, BCC, CCC. Pro realistickou teorii popisující dvanáct fermionů (šest leptonů, šest kvarků) a třináct bozonů (foton, Higgs, W+, W-, Z, osm gluonů) a zahrnujících kubické a kvartické interakční členy pak samozřejmě všech možných vazebních konstant může být strašně moc. Standardní model je úspěšný právě proto, že z nepřeberného množství všech těchto potenciálně myslitelných vazebních konstant plus pětadvaceti hmotností ponechává pouze 26 nezávislých parametrů (zde počítám i elementy tzv. CKM matice a PMNS matice, výklad by byl nadlouho). Drtivé množství vazebních konstant či jejich hodnot je vyloučeno z požadavku vnitřní logické konzistence té teorie, mj. jsou dány do těsných vztahů hmotnosti mnoha částic se zbylými vazebními konstantami.
Tzn. že přesto, že díky Higgsovu mechanismu dokážeme pochopit vznik hmotností („hmotností prvého druhu“) u částic, které měly být původně nehmotné, tak číselnou hodnotu získat neumíme, protože přes všechno to úsilí v teorii zbylo oněch 26 volných parametrů. Nicméně pro získání těchto volných parametrů je potřeba provést jen 26 nezávislých měření. Všechny další předpovědi pro nekonečně mnoho možných experimentálních uspořádání a měření je pak standardní model schopen v principu dát. Tak např. v teorii zbývá jen několik málo nezávislých vazebních konstant, všechny ostatní mohou být vyjádřeny pomocí těchto několika plus pomocí naměřených hmotností částic.
Tzn. že skutečnost, že standardní model neumí předpovědět hmotnosti všech částic, je způsobem obrovským množstvím potenciálně myslitelných vazebních konstant, které mohou v teorii tolika částic být – počet těchto konstant roste řádově s třetí mocninou počtu částic v případě kubické interakce, a se čtvrtou mocninou v případě kvartické interakce (s pátou mocninou v případě kvintické interakce, atd.). Z důvodů vnitřní logické konzistence jsou vyloučeny všechny členy pátého a vyššího stupně, zbývají tudíž jen vazební konstanty jen pro kubickou a kvartickou interakci, i těch je ale pro 12 fermionů a 13 bosonů nepřeberně mnoho. To, že z těchto všech parametrů jich nakonec zbylo jen 26, je obrovský úspěch, hlavně už proto, že dlouhá léta to vypadalo, že všechny teorie jsou logicky sporné. Standardní model byl prvou teorií, která byla vnitřně logicky konzistentní, která popisovala všechny tehdy známé částice, ovšem cenou za tuto vnitřní konzistenci bylo to, že si vynutila existenci obrovského množství vnitřních vazeb mezi mnoha různými a zdánlivě nezávislými parametry, plus si vynutila existence do té doby neznámých částic – kvarku c, po objevení třetí generace i kvarku t, tauonového neutrina, výměnných bosonů W+, W- a Z, a jako posledního Higgsova bosonu. Všechny tyto částice nejen že byly objeveny, ale byly u nich nalezeny i přesně předpovězené diskrétní charakteristiky (např. spin, náboj, mnohá kvantová čísla), dále bylo potvrzeno, v jakých interakcích se vyskytují a v jakých ne, a byly ověřeny mnohé dynamické charakteristiky, jako jsou účinné průřezy, způsoby rozpadů a jejich větvící poměry, doby života. Za skoro čtyři desetiletí existence standardního modelu byly provedeny milióny měření, a dodnes nebyl nalezen náznak fyziky, který by do tohoto modelu nepasoval (pouze došlo např. akceptaci nenulovosti hmot neutrin – standardní model nenulové hmoty umožňoval, protože koneckonců patřily mezi těch 26 volných parametrů, pouze se z důvodů jednoduchosti předpokládalo, že by hmotnosti neutrin mohly být nulové, protože po dlouhou dobu neexistoval experimentální podklad pro jejich nenulovost, tento podklad byl získán díky přesnějším experimentům až před několika lety).
Frank Wilczek ve své knize „The Lightness of Being: Mass, Ether, and the Unification of Forces“ (vyšla loni v češtině pod názvem „Lehkost bytí aneb Bytí jako světlo“) píše výhradně o této druhé, sekundární hmotnosti. Proto také mnohokrát připomíná, že mechanismy, které popisuje, vysvětlují pouze 95 procent hmotnosti. Bohužel ne každému čtenáři je jasné, že tato hmotnost se týká pouze hadronů, tj. částic interagujících silnou interakcí (tj. baryonů a mezonů, sestávajících z kvarků a v případě mezonů i antikvarků), nikoliv už leptonů, jako jsou elektron, mion, tauon, a jim odpovídající neutrina. Pozorný čtenář najde jen zmínky, že s nepřesností činící maximálně několik málo procent lze tuto hmotnost spočíst pomocí tzv. light QCD, zjednodušené verze kvantové chromodynamiky počítající pouze se třemi místo šesti kvarků. Bohužel pouze zasvěcenějšímu čtenáři je tím pádem jasné, že tím pádem je řeč pouze o kvarcích a gluonech, protože QCD i light QCD leptony nepopisují.
Frank Wilczek je samozřejmě odborník na slovo vzatý, je nositelem Nobelovy ceny za fyziku za rok 2004 za objev asymptotické volnosti v teorii silné interakce. Jako každý takovýto na slovo vzatý expert má neoddiskutovatelné právo vložit do svého výkladu svůj vlastní, osobitý náhled na mnoho dodnes otevřených problému, stejně tak jako použít jakkoliv originální a neobvyklou terminologii či jakoukoliv představu o elementech, které by mohly být elementárnějšími, než je třeba vakuum – pro takovýto hypotetický prazáklad používá Wilczek pojem Grid, v českém překladu je použit pojem Tkanivo. Na toto všechno má samozřejmě tak renomovaný autor plné právo – bohužel druhou stranou mince pak je to, že laický čtenář nemá šanci rozlišit, že Grid či Tkanivo, které autor zasvěceně popisuje, zdaleka není všeobecně přijímanou představou, bez ohledu na souhlas s dílčími autorovými argumenty. Bohužel jediná cesta, jak může laický čtenář odlišit ty všeobecně přijímané představy od těch privátně autorových, je přečíst podobných popularizačních knížek hodně, a od různých autorů – jako jsou např. Roger Penrose, Stephen Hawking, Steven Weinberg, John Barrow, Michio Kaku, Lee Smolin, mnozí popularizátoři strunových teorií, atd. atd.. Teprve poté čtenář, ač laik, zjistí, které představy jsou součástí širšího konsensu, a které už patří spíše do specifického vidění (či „přání, jak by tomu mohlo být“) toho kterého autora.
standardný model
Maroš Štulajter,2012-07-09 23:05:09
čo som písal o tom top kvarku v štandardnom modeli "vzhľadom k tomu štandardný model nepopisuje dostatočne hmotnosť top kvarku, tak ako nepopisuje dostatočne oscilácie neutrín, takže môže presahovať za štandardný model.
Hmotnosti kvarků
Vladimír Wagner,2012-07-10 09:12:09
Standardní model však nepředpovídá hmotnost žádného kvarku (je potřeba k tomu změřit potřebné parametry - viz blíže povídání P. Brože). Stejně tak nepopisuje parametry míchání kvarků. A stejně tak nepředpovídá hmotnosti neutrin a parametry míchání jejich stavů. To, že se původně uvažovala nulová klidová hmotnost neutrin a neexistence oscilací bylo tím, že je to nejjednodušší a představa tak dramatického rozdílu mezi hmotnostmi kvarků a nabitých leptonů oproti neutrinům byla méně přijatelná než, že neutrina mají z nějakých důvodů hmotnost nulovou. Hierarchie hmotností u kvarků a leptonů je tak závislá na volných parametrech, stejně jako míchání v kvarkovém a neutrinovém sektoru. To, že jsou potřeba desítky volných parametrů, je jedním z důvodů, proč si teoretici myslí, že musí existovat teorie za standardním modelem. To ovšem nic neříká o tom, jaká by ta teorie měla být. A v tomto ohledu, alespoň podle mého názoru, top kvark nijak nevystupuje oproti ostatním kvarkům. Jedině tím, že jeho hmotnost je hodně velká a je větší šance, že se v jeho vlastnostech může vliv nové teorie (její odlišnost od standardního modelu) více projevit.
top kvark
Maroš Štulajter,2012-07-09 17:01:19
pred chvíľou som čítal že top kvark sa nemôže celkom zaradiť do štandardného modelu ale vzhľadom na svoju hmotnosť ide až za štandardný model ale na grafoch je zakreslený vnútri štandardného modelu môžte o tom niečo napísať?
Top kvark
Vladimír Wagner,2012-07-09 20:39:37
je součástí standardního modelu, dokonce byla jeho existence na základě symetrií, které se ve standardním modelu vyskytují, předpovězena před jeho objevem. Kde jste četl, že se nezařazuje do standardního modelu? Připomínám, že standardní model nepředpovídá hmotnosti kvarků. Ty jsou parametry modelu a musí být zjištěny experimentem.
Možná, že v tom, co jste četl, měli na mysli, že díky své velké hmotnosti může být nejcitlivější i na vlivy fyziky za standardním modelem. Ale, pokud vím, tak zatím na jeho vlastnostech nebyla nalezena žádná jasně prokázaná odchylka od standardního modelu, která by pomohla určit vlastnosti teorie za standardním modelem.
Animovaný higgs
Petr Toman,2012-07-06 21:17:25
Pěkné animované povídání o Higgsově bosonu:
http://vimeo.com/41038445 (animace začíná 0:37)
Hmotnost castic?
Peter Peter,2012-07-06 13:08:24
To ze higgsov boson "dava" casticiam hmosnost je zname z takmer kazdeho clanku na tuto temu. Mna by vsak zaujimalo, aky sposobom sa to deje?
Aj v tomto clanku bolo spomenute: "Nové částice, které experimenty na urychlovači LHC hledají a z nichž nejznámější je higgs, žijí jen velice krátce a rychle se rozpadají na jiné."
Dalej v clanku sa pise: "Higgsův mechanismus navržený skotským fyzikem Peterem Higgsem, který takové generování hmotnosti u částic popisuje,..."
Kedze castice maju hmostnost, znamena to ze sa v nich higgs neustale generuje a nasledne rozpada?
Které ?
Mojmir Kosco,2012-07-05 09:05:20
Které další hypotetické elementární nebo složené částice patří do standardního modelu? A jak je to s gravitonem ?
Částice standardního modelu
Vladimír Wagner,2012-07-05 09:38:42
Higgsův boson je poslední "opravdu elementární" částicí, která byla ve standardním modelu pouze hypotetická a nebyla prokázána. Takže z toho hlediska už je standardní model uzavřen (připomínám, že je prokázáno, že mohou být pouze tři generace kvarků a leptonů s lehkými neutriny, jaké známe ve standardním modelu). Takže neobjeveno je jen velké množství baryounů a mezonů, které vznikají složením různých kvarků různým způsobem. Trochu to teď připomíná atomová jádra po objevu neutronu. Pak už také jeho konstituentní částice byly známy všechny, ale pořád je spousta hypotetických izotopů i prvků, které je potřeba objevit (úmyslně zapomínám na hyperjádra a antijádra).
Pro úplného laika
Vladimír Wagner,2012-07-05 08:51:55
Napřed díky Pavlovi Brožovi, který stabilně dělá diskuzi zajímavější článku :-) A teď k otázce Libora Kisse. Higgsova částice je důležitou komponentou standardního modelu. Takže určení jeho hmotnosti (kterou model nepředpovídá a je jeden z volných parametrů tohoto modelu) umožňuje jeho zpřesnění a zpřesnění jeho předpovědí. Přesná změření jeho dalších vlastností (třeba pravděpodobností různých jeho rozpadů) umožňuje další zpřesnění. Zpřesněné předpovědi o chování různých částic a průběhu různých reakcí pak umožňuje jejich konfrontaci s přesnými měřeními získanými nejen na LHC a hledání odchylek od standardního modelu. Pokud se takové odchylky najdou, mohly by ukázat na to, jaká teorie funguje nad standardním modelem.
Od uplneho laika
Libor Kiss,2012-07-04 23:12:55
Hon na Higgsa uz bol spominany tolko krat, ze mi nepripada nijako zvlastne, ze ho konecne objavili. Mal som dojem (!), ze existuje spusta castic, ktore svojou existenciou potvrdzuju standardny model, a preto by higgs, ako dalsia castica z mnohych, nemal vzbudzovat taku extaticku vlnu nadsenia.
Znamena to teda, ze uz sa teoretici nemusia zaoberat teoriami veducimi do slepej ulicky? Zuzuje sa tym pocet teorii vsetkeho? Alebo co sa teda vlastne zmenilo? Aky je rozdiel medzi teraz a predtým?
Este jedno prirovnanie: Pripada mi to, akoby fyzici niekde na zajazde cakali pri pokazenom autobuse, kym im automechanici nenahradia chybajucu suciastku do motora. Vsetci netrpezlivo cakaju, lebo by radi sli dalej, ale nemozu. No a ked im automechanik konecne povie, ze uz novu suciastku konecne nasli, idu sa vsetci pri autobuse zblaznit od stastia. Výlet moze pokracovat dalej.
fotón
Maroš Štulajter,2012-07-04 22:23:09
je predstaviteľom elmg poľa. v pokoji síce nemá hmotnosť, vlastne neexistuje. fotón má energiu danú planckovou konštantou a frekvenciou. keďže energia je závislá na hmotnosti (e=mc^2, znamená že fotón má relativistickú hmotnosť. vieme že leptóny si naberajú hmotnosť z higgsovho poľa trochu ináč ako kvarky tak by mi s toho vyplývalo ak uvážim že elektrón má svoje vlnové vlastnosti tak relativistický fotón s energiou planckovej konštanty a frekvenciou 1 by mal byť najľahšia častica vo vesmíre.
higgsovo pole
Roman Rodak,2012-07-04 15:17:54
Viem si celkom dobre predstaviť, že existuje nejaká častica, konkrétne bozón, ktorý má určité špeciálne vlastnosti a odlišuje sa od všetkých ostatných. Ale čo je to higgsovo pole? Ako konkrétne súvisí s higgsovým bozónom? Je to napr. niečo také ako fotón a elektromagnetické pole? Vo vysvetleniach určených pre laikov sa často spomína, že pole kladie akýsi odpor časticiam ktoré sa v ňom pohybujú, ale toto mi silne zaváňa éterom, čiže predpokladám, že to bude extrémne zjednodušenie situácie. Také vysvetlenie mi nestačí napriek tomu že som laik. Alebo je tu predsa nejaké absolútne pole, len sa o tom moc nehovorí? (a čo na to potom pán Einstein?). Respektíve keď sa hovorí o pohybe v poli, myslí sa tým skutočný pohyb v priestore, alebo je to len nejaká prenesená predstava pohybu?
Troška veľa otázok naraz, ale keď už to vyzerá že ten higgs predsa len existuje...
zjevně si nedokážete představit
Asdf Fdsa,2012-07-05 00:01:05
Zhruba: Higgsů boson je kvantum Higgsova pole.
ad pole, částice, Higgs a hmotnosti
Pavel Brož,2012-07-05 00:21:45
Existuje takové z pohledu laika trošku babylonské zmatení jazyků, když je řeč o částicích a polích. Tato věc se jen v málokterých populárně naučných knížkách vysvětluje, pokusím se to tady malilinko přiblížit, nicméně také se musím uchýlit k dílčím zjednodušením.
Zhruba řečeno lze říct, že teorie elementárních částic a kvantová teorie pole jsou synonyma. Elementární částice jsou kvanta, která se získají, když se kvantuje systém, který má v nekvantové fyzice nekonečně mnoho stupňů volnosti – v klasické fyzice máme dva modely systémů, který má nekonečně stupňů volnosti, jedním modelem je mechanické kontinuum, což je spojitý model hmoty (tímto kontinuem může být jak pevná látka, tak kapalina nebo plyn), a druhým modelem je klasické pole, jako je elektromagnetické či gravitační pole. Mezi mechanickým kontinuem a klasickým polem je rozdíl v tom, že pohybové rovnice mechanického kontinua jsou získány „kontinualizací“ Newtonových rovnic (tento termín jsem právě vymyslel, nikde ho nehledejte – jde čistě jen o to, že dostatečně maličká část toho kontinua se musí chovat jako hmotný bod odpovídající hmotnosti a rychlosti), zatímco pohybové rovnice klasického pole musí být nalezeny nezávisle (např. Maxwellovy rovnice popisující elektromagnetické pole v žádném případě nemohou být odvozeny z Newtonových rovnic; totéž platí také o Einsteinových rovnicích popisujících gravitační pole).
Klasická dynamika se vlastně dá rozdělit na mechaniku hmotných bodů, mechaniku kontinua a (klasickou) teorii pole. Z tohoto popisu jsem vynechal termodynamiku, kterážto zastává svou vlastní svébytnou pozici, která je velice obtížně zaškatulkovatelná; pro nyní si s úvahami o ní nebudeme věci komplikovat.
Klasická dynamika přiřazuje každému systému jakožto celku, ale také i všem jeho komponentám jednotlivě, jednak odpovídající kinetickou energii a jednak odpovídající energii potenciální, a také energii celkovou, která je součtem kinetické a potenciální. Pro celkovou energii izolovaného systému nenacházejícího se ve vnějším poli platí za jistých dosti obecných podmínek zákon zachování. Podobně jako kinetická energie, jde systému i jeho částem připsat hybnost a moment hybnosti, a také pro celkovou hybnost a celkový moment hybnosti systému platí za jistých dosti obecných podmínek zákon zachování.
Důležité je, že v celé klasické fyzice neexistuje žádný způsob, který by dovoloval systému nabývat jenom některých hodnot celkové energie či celkového momentu hybnosti. Jakmile totiž existuje nějaký systém s nějakou hodnotou celkové energie, tak vždycky lze realizovat jiný stav téhož systému s jinou libovolně zvolenou hodnotou celkové energie. Totéž platí pro celkový moment hybnosti. Tak např. máte-li rotující kolo, tak toto kolo disponuje nějakou hodnotou momentu hybnosti. Tuto hodnotu můžete zvýšit či snížit zvýšením či snížením rychlosti otáčení kola, a to můžete v klasické fyzice udělat spojitě, tj. získat ve výsledku libovolnou hodnotu momentu hybnosti.
Kvantová teorie vznikla na základě množství empirických faktů dosvědčujících, že mikroskopické systémy, jako jsou atomy, molekuly, ale třeba také dostatečně detailně zkoumané světlo či obecněji elektromagnetické záření, nemůže být uvedeno do stavu o libovolné hodnotě celkové energie či momentu hybnosti. Projevem této skutečnosti jsou u atomů charakteristická emisní a absorpční spektra, která nám ve spektroskopii umožňují jakožto charakteristické otisky prstů identifikovat látky byť se nacházející v miliónech světelných let vzdálených galaxiích. U elektromagnetického záření je projevem této skutečnosti to, že pro danou frekvenci může být celková energie zářivého pole dána jenom pomocí celých násobků základního energetického kvanta daného touto frekvencí (zde se dopouštím jistého zjednodušení spočívajícího v tom, že uvažuji jen tzv. Fokovy stavy, nicméně budiž). Důsledkem toho, že celková energie elektromagnetického zářivého pole se může měnit pouze o celé násobky nenulových diskrétních kvant energie (kterým se říká fotony), je mj. Planckův vyzařovací zákon, který např. určuje, kterou vlnovou délku vyzařuje těleso dané teploty jakožto dominantní vlnovou délku (tento zákon tedy vysvětluje, proč je při nějaké teplotě žhavé železo červené, a proč při vyšší teplotě je žluté, a také samozřejmě říká při kterých konkrétních teplotách má tu či onu barvu).
Ačkoliv byla vlastně kvantová teorie „počata“ právě u popisu nezvyklých vyzařovacích vlastností elektromagnetického pole, totiž že musí existovat jeho kvanta (za zakladatelskou ideu kvantové teorie bývá považována právě ta Planckova hypotéza z roku 1900), tak následně byl rozvoj kvantové teorie na několik desetiletí pod patronátem kvantové mechaniky – kvantová mechanika je kvantovou verzí klasické mechaniky hmotných bodů; mechanika hmotných bodů ale netvoří celou klasickou fyziku, tu kromě ní tvoří i mechanika kontinua a klasická teorie pole. Klasická mechanika hmotných bodů je ale v jistém smyslu jednodušší, než mechanika kontinua či klasická teorie pole, a to přesně se ukázalo rozhodující pro rodící se kvantovou teorii, které se mnohem dříve dařilo novým, „kvantovým“ způsobem popisovat systémy, které v klasické fyzice korespondovaly právě těm hmotných bodům. Např. kvantový popis atomů a později i molekul byl popisem systémů, které v klasické podobě sestávaly z elektricky nabitých hmotných bodů. Přitom skutečnost, že tyto body byly elektricky nabité, na tehdejší úrovni popisu neznamenala komplikaci vnesením prvků elektromagnetického pole, protože pokud se částice nepohybují rychlostí srovnatelnou s rychlostí světla, tak lze polní popis nahradit Coulombickým působením na dálku (je tomu opravdu tak, pojem pole je nevyhnutelně nutno začít používat teprve až když dostatečně rychle se pohybující částice začínají při svém nerovnoměrném pohybu vytvářet záření, které odnáší část energie a hybnosti, o které tyto částice přichází; tyto tzv. radiační ztráty jsou při nerelativistických rychlostech zanedbatelné, proto je v dílčích případech možné se v nerelativistickém režimu bez pojmu pole obejít).
Časem ale byly nalezeny kvantovací postupy umožňující vytvořit kvantové verze i pro zbývající části klasické fyziky, tj. pro mechaniku kontinua a klasickou teorii pole. Odpovídající teoretická disciplína se nejčastěji nazývá kvantová teorie pole. Kvantovou teorii pole můžeme získat tak, že vezmeme např. klasickou teorii pole, a podrobíme ji proceduře kvantování. Získáme systém, který ve shodě s pravidly kvantové teorie nemůže nabývat libovolné energie, ale pouze energie získané součtem energií nějakých základních kvant. Ukazuje se, že každé takovéto kvantum disponuje kromě energie i určitou hybností, a také se mu dají přiřadit další charakteristiky, jako je např. spin. Ve výsledku se ukáže, že každá známá elementární částice může být ve skutečnosti popsána jakožto kvantum nějakého pole. Např. elektron, mion, tauon, či kterékoliv ze tří druhů neutrin jsou kvanty odpovídajících spinorových polí pro příslušné hodnoty hmotnosti (tato pole jsou popisována Diracovou rovnicí, což je právě ten na začátku zmíněný pohybový zákon pro tato pole). Totéž platí pro všech šest druhů kvarků. Foton, gluony a intermediální výměnné bozony jsou opět kvanty odpovídajících polí (např. foton je kvantem pole elektromagnetického, popisovaného Maxwellovými rovnicemi coby pohybovými rovnicemi pro toto pole).
Možná by vás zajímalo, kam se podělo kvantování mechanického kontinua – také pro tuto část klasické fyziky se dá vytvořit odpovídající kvantová verze, odpovídající kvanta ale nenazýváme částicemi, ale kvazičásticemi. Jedná se o podivnůstky typu fonony (coby kvanta „zvuku“, tj. kmitů mechanického kontinua), rotony, polarony, magnony, a mnohé další. Nazýváme je kvazičástice a nikoliv částice, abychom zdůraznili, že nemohou existovat samostatně mimo ono kvantované kontinuum. Připomeňme si, že základním krédem kvantové teorie je empirický fakt, že systém nemůže nabývat libovolných hodnot energie, ale že může nabývat jenom energií (anebo jindy momentu hybnosti, atd.), která se může měnit jen po nějakých nedělitelných kvantech. V kvantovém obrazu klasické teorie pole se tato kvanta daří úspěšně ztotožnit s elementárními částicemi. V kvantovém obrazu klasické mechaniky kontinua se toto ale nedaří, nic takového, jako je třeba polaron, jakožto autonomní elementární částice neexistuje. Přesto se ale energie toho kontinua také může měnit jenom po nějakých kvantech. Ukazuje se, že tato kvanta můžeme považovat za jakési kolektivní excitace toho prostředí. Tak např. fonon je kvantem vibrací krystalové mřížky, i jej energie je kvantována. Ovšem bez té krystalové mřížky by fonon samostatně existovat nemohl.
Upozorňuje, že tento popis je do značné míry zjednodušený, protože kvazičástice lze získat také při kvantování klasického pole, akorát že k tomu musíme přibalit i něco více, jako je např. to kontinuum, anebo krystalická mřížka, anebo předepsaná struktura elektronových vodivostních pásů, atd. atd.. Zhruba řečeno, o elementárních částicích hovoříme tam, kde pracujeme s kvanty klasických polí nacházejících se ve vakuu, zatímco o kvazičásticích hovoříme tam, kde pracujeme s kvanty v nějakém kontinuu daných vlastností, anebo s kvanty polí šířících se nikoliv ve vakuu (např. může jít i propagaci běžného elektromagnetického pole v silně nelineárním prostředí, např. krystalu, amorfní látce, kapalině či plynu – kvanta takovéhoto pole nejsou nehmotná, ale mají hmotnost v důsledku komplikované neustále probíhající interakce s tím nelineárním prostředím, a proto nejde o elementární částice, ale o kvanta kolektivních procesů, vlastně o kolektivní excitace systému sestávajícího se z procházejícího elektromagnetického pole a s ním silně interagujícího nelineárního prostředí.
Nyní bychom mohli zavětřit jistou podobnost s Higgsovým polem a tím, jak toto pole má údajně dávat hmotnost ostatním částicím. Před chvílí bylo zmíněno kvantum elektromagnetického pole, které bylo při průchodu nelineárním prostředím hmotné, ačkoliv ve vakuu je nehmotné (foton má opravdu ve vakuu nulovou klidovou hmotnost). Tu hmotnost při průchodu tím nelineárním prostředím získalo právě díky té masivní interakci s tím prostředím.
Higgsovo pole ve skutečnosti dělá něco velice podobného. Také jeho interakce s ostatními původně nehmotnými částicemi je činí hmotné. A navíc sám Higgs, tj. kvantum tohoto pole, získává tímto způsobem svou hmotnost, protože umí interagovat (na rozdíl od třeba elektromagnetického pole) samo se sebou.
Je dobré si ale uvědomit, že Higgsovo pole nečiní hmotnými všechny částice, ale jen některé. Kromě už zmíněných fotonů, ve vakuu nehmotných, zůstávají nehmotnými také gluony, částice zprostředkující silnou interakci mezi kvarky, drží je např. uvnitř nukleonů. A navíc, i ty částice, které získávají svou hmotnost díky Higgsovu poli, ji získávají různou, tak např. elektron, mion, tauon, tři druhy neutrin a všech šest druhů kvarků, celkem tedy dvanáct leptonů, mají všechny rozdílné hmotnosti. Čím to je, že některé částice hmotnost nezískají vůbec a ty ostatní získají každá jinou, a proč mají zrovna takovou, jakou mají?
Na některé z těchto otázek odpověď v rámci standardního modelu existuje, např. proč některé částice nezískají díky Higgsovu poli hmotnost – je to dáno druhem té vazby mezi Higgsovým polem a příslušnými nehmotnými částicemi. Jiné otázky standardní model zodpovědět neumí. Standardní model je schopen vysvětlit, proč např. leptony hmoty nenulové mají, a dokonce umí hodnoty mnohých těchto hmotností dát do exaktních vztahů s různými vazbovými konstantami v teorii figurujícími (tzn. že zdaleka ne všechny konstanty vystupující ve standardním modelu jsou na sobě nezávislé). Přesto všechno ale stále existuje nekonečná potenciální variabilita mezi zbylými nezávislými parametry, která umožňuje, aby hmotné elementární částice mohly mít teoreticky libovolné hmotnosti, svázané vůči sobě pouze množstvím nerovností (tak např. neutrální výměnný bozon Z musí být podle standardního modelu vždy hmotnější, než nabité výměnné bozony W – standardní model už ale neurčuje o kolik může být bozon Z hmotnější).
Roman Rodak,2012-07-07 14:35:07
Taktiež ďakujem za super vysvetlenie. No jedna vec mi nejde do hlavy - každé pole má nejaký svoj zdroj a na každom mieste môže mať inú intenzitu. Tým pádom aj sila interakcie sa neustále mení. No častice majú hmotnosť stále tú istú - znamená to, že higgsovo pole je homogénne v celom vesmíre?
Jiří Pinkava má plně pravdu
Vladimír Wagner,2012-07-04 14:52:51
Už jsem si toho všiml také. A poprosil redakci o opravu. V mém textu, který jsem psal během sledování přednášek v CERNu a krátce po něm, mi vypadla jednička. Správně má být 133. Text jsem psal na své zvyklosti hrozně narychlo, takže pokud narazíte ještě na nějaké překlepy nebo jiné chybky, budu vděčný za upozornění. Díky.
33 vs 133 ?
Jiří Pinkava,2012-07-04 14:37:23
Nevypadla náhodou při přepisu (někde) jednička? pak by to vycházelo.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce