Nedávno vědci z Číny a Jižní Koreje slavili úspěch v odhalování vlastností neutrin (viz zde a zde). Přispěli k pochopení oscilací neutrin, které patří mezi „speciality“ kvantového světa. Experimenty popisované nyní studují vlastnosti, které se také nevyskytují v klasické ale pouze kvantové fyzice a ukazují možnosti využití propletení kvantových stavů při kvantové teleportaci.
Propletené stavy
Specifickým kvantovým vlastnostem se věnuje článek o podivnostech kvantového světa. Vysvětluje i jak propletené stavy vznikají. V kvantovém světě je stav částice nebo systému částic popsán vlnovou funkcí. Měřitelné fyzikální veličiny, jako jsou rychlost, hybnost, energie částice nebo dalších objektů tato funkce přímo neudává, ale mohou z ní být získány. Velmi často však vlnová funkce neumožňuje pro konkrétní jedno měření určit přesné hodnoty měřitelných veličin, ale pouze pravděpodobnost, se kterou se při měření vyskytne určitá hodnota příslušné veličiny.
V kvantové fyzice se zavádí qbit, což je kvantový ekvivalent klasického bitu. Zatímco klasický bit může nabývat pouze hodnoty 0 nebo 1, kvantový qbit je vlastně přenesení kvantového stavu popsaného vlnovou funkcí, který je superpozicí dvou čistých stavů a při měření dává s danou pravděpodobností hodnotu 0 a 1. Pochopitelně mezi možnými stavy jsou i čisté stavy, kdy dostaneme hodnotu 0 nebo 1 se stoprocentní pravděpodobností a druhý stav s pravděpodobností nulovou. Pokud by se využívaly pouze tyto dva čisté stavy, přejde se od práce s qbity k práci s klasickými bity.
Práce s qbity a vlastnostmi kvantových stavů umožňuje provádět řadu výpočetních operací, které klasické počítání neumožňuje. Proto když se podaří zkonstruovat kvantové počítače, přinese to radikální pokrok nejen ve výpočetní technice.
Pokud v nějakém uzavřeném systému částic pro danou fyzikální veličinu platí zákon zachování, změření konkrétní hodnoty této veličiny u jedné z částic určuje, jakou hodnotu mají dohromady zbylé částice. Protože kvantová funkce je popsána pro celý systém v prostoru a kvantová teorie je nelokální (změny při měření nastávají v jediném okamžiku v celém prostoru), při změření hodnoty dané veličiny u jedné částice z tzv. propleteného kvantového stavu dvou částic je hodnota této veličiny u druhé částice okamžitě dána bez ohledu na jejich okamžitou vzdálenost.
Propletené stavy lze využít k teleportaci kvantové informace. S kolegou (říkejme mu klasicky „Bob“, naše funkce je označována jako „Alice“), se kterým si chceme kvantové stavy přenášet, si každý vezmeme jednu částici z kvantového propleteného systému, který jsme obdrželi od „Charlieho“. Když budeme chtít teleportovat kvantový stav, který Charlie dodal nám (Alici) i Bobovi, provedeme s tímto kvantovým stavem a svoji částí propleteného systému specifické měření. Tímto měřením (hovoří se o měření Bellova stavu) dojde díky nelokálnosti kvantové fyziky a společné vlnové funkci k ovlivnění Bobovy částice. Pokud mu klasickou cestou pošleme výsledek našeho měření, bude vědět, jakým způsobem reprodukovat na své části propleteného systému kvantový stav, který mu chceme předat.
K ovlivnění druhé částice z propleteného stavu sice dochází okamžitě, ale reprodukci přenášeného kvantového stavu může kolega provést jedině po obdržení výsledku měření provedeného na první částici propleteného stavu. A výsledek se dá posílat nejrychleji rychlostí světla, takže nedochází k přenosu informace nadsvětelnou rychlostí a narušení kauzality. Paradoxem je i to, že kvantový stav, který je odesílán, se na jednom místě interakcí (měřením) zničí, zároveň se ale na místě jiném pomocí druhé částice z původní kvantově propletené dvojice znovu vytvoří. Stále však máme pouze jeden tento stav. Nejde tak provádět klonování kvantových stavů.

Nové úspěchy s kvantovou teleportací na velkou vzdálenost
Jak bylo popsáno v článku o podivnostech kvantového světa, kvantovou teleportaci šlo zatím testovat na vzdálenosti několika kilometrů. Propletené stavy se daří získávat u fotonů a dalších částic, atomů i komplexnějších systémů. Testy teleportace na velké vzdálenosti probíhají právě s využitím polarizovaných fotonů a právě polarizace těchto částic a její vzájemná souvislost u páru fotonů v propleteném stavu umožňuje studium kvantové teleportace. Podrobnější vysvětlení pojmu polarizace u světla a souvislost se spinem a helicitou fotonů je ve zmíněném článku. Důležité je, že přenos se musí uskutečňovat pomocí jednoho fotonu, který nesmí během své existence interagovat tak, aby došlo ke kolapsu vlnové funkce a zrušení původního kvantového propleteného stavu. Nelze tak použít zesilovač na dráze sloužící k přenosu kvantových stavů od vysílače k přijímači. Při prvních experimentech se zkoušelo hlavně posílání kvantových stavů a teleportace pomocí optických vláken. Nyní se přechází k přenosu volným prostorem. Cílem je možnost kvantové komunikace v dosahu odpovídajícímu vzdálenosti telekomunikačních satelitů alespoň na nízkých oběžných drahách, aby bylo možné využívat při komunikaci výhod kvantové kryptografie. Ta umožňuje velice spolehlivé zašifrování komunikace i její bezpečnost při pokusu o odposlouchávání jinou osobou, která by svým měřením propletené stavy narušila. Takové zničení příslušného kvantového stavu by odposlech prozradilo.
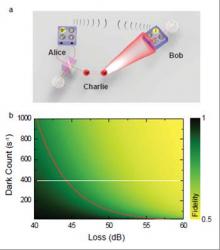
V květnu letošního roku vyšlo několik článků, které referovaly o úspěších v kvantové teleportaci na velmi velkou vzdálenost. V předchozím článku byl popisován úspěšný přenos na vzdálenost 18 km. Zmiňoval se i o čínském experimentu X.-M. Yina a jeho kolegů, který se týkal kvantové teleportace na vzdálenost 16 km. V novém experimentu, který provedli také čínští fyzikové a prvním autorem publikace je rovněž Juan Yin, se podařila kvantová teleportace na vzdálenost 97 km přes jezero Quinghai v západní Číně. Propletené stavy fotonů vědci vytvářeli pomocí svazku ultrafialového světla z laseru o výkonu 1,3 W a speciální optické sestavy. Ta obsahuje nelineární krystaly, většinou známé jako BBO (podle jejich chemického složení - BaB2O4), které dokáží vytvořit z jednoho fotonu dvojici polarizovaných fotonů v kvantovém propleteném stavu. K lepšímu pochopení si můžeme pokus popsat následovně: Máme část označenou opět jako „Charlie“. Ta vytvoří dvojici částic v propleteném stavu. Jeden foton z tohoto páru pošle do části „Alice“, která je blízko. Druhý do vzdálenější části „Bob“, přičemž se jako vysílač použije dalekohled (refraktor) o průměru 127 mm. „Bob“ na opačné straně jezera jako přijímač využívá zrcadlový teleskop s průměrem 400 mm. Charlie vytvoří pomocí stejného ultrafialového laseru pro Alici stav, který potřebuje teleportovat. Alice jej nechá interagovat s původním propleteným fotonem, který má u sebe. Zároveň pošle výsledky svého měření pomocí klasického bezdrátového spojení Bobovi. Ten pak může pomocí své části propleteného systému a výsledků vlastního měření rekonstruovat její teleportovaný kvantový stav. Pochopitelně jsou při takové komunikaci velké ztráty a je třeba posílat velký počet fotonů. Samotná rekonstrukce také není dokonalá, protože fotony mohou cestou interagovat a tímto „měřením“ dojde ke zničení propleteného kvantového stavu. K synchronizaci celého systému se využívá GPS. Úspěšnost teleportace s využitím šesti různých kvantových stavů byla u zachycených a testovaných teleportací zhruba 80 %. Vzhledem k velké vzdálenosti byly totiž i při využití dalekohledu značné ztráty v kvantovém kanále přenosu až na úrovni 35 - 53 dB.

Pokrok je hlavně v tom, že se testoval nejen přenos propleteného stavu, kolaps jeho vlnové funkce a korelace mezi polarizací jeho dvou částic, jako ve většině předchozích experimentů, ale přímo celý proces kvantové teleportace. I když stále zůstávají slabá místa, například zdrojem teleportovaných kvantových stavů byl stejný laser produkující propletené stavy a k testovacímu měření u skupiny Alice došlo ještě před tím, než druhý foton z propleteného stavu dorazil ke skupině Bob, je už celý proces mnohem blíže budoucím potřebám při reálném využívání kvantové teleportace.
Minulý článek rovněž popsal případ testování přenosu a zachování propleteného stavu a jeho kolapsu na vzdálenost 144 km, který se odehrával mezi dvěma lokalitami v Kanárském souostroví. V tomto případě se jako vysílač využíval přístroj na ostrově La Palma (Jacobus Kapteyn Telescope), kde je Charlie a Alice a jako přijímač je teleskop, který je součástí Optical Ground Station (OGS) organizace ESA na ostrově Tenerife, kde je Bob. Průměr přijímacího detektoru je jeden metr. Těsně po oznámení výsledku čínské skupiny oznámila nové výsledky i skupina pracující právě na Kanárských ostrovech. Tým vedený Antonem Zeilingerem tentokrát netestoval pouze zachování propleteného stavu. Při tak velké vzdálenosti částic provedl i celý proces kvantové teleportace. Tento extrémní výkon se vědcům podařil díky řadě vylepšených technologií, s jejichž pomocí získali daleko intenzivnější zdroj propletených fotonů. Detekci prováděli fyzikové pomocí velmi citlivých jednofotonových detektorů s velmi nízkým šumem. Velkou výzvou pak byla časová synchronizace. Její přesnost na úrovni 10 ns, jež se u tohoto experimentu dala dosáhnout pomocí GPS, nepostačovala, proto se využila nově vyvinutá metoda využívající právě testování pomocí kvantově propletených stavů.

V tomto případě se fyzikové museli vypořádávat i se značnou nepřízní počasí včetně k písečné bouře a sněžení. To, že se jim i za zhoršených podmínek dařilo realizovat kvantovou teleportaci, je dobrou předzvěstí možnosti komunikace se satelity na nízké oběžné dráze. Ty sice létají ve vzdálenostech nad zemským povrchem, které jsou třikrát větší než vzdálenost, na které probíhal pozemní pokus, ale vrchní vrstvy atmosféry jsou mnohem průhlednější, takže existuje naděje, že by se tato komunikace mohla zdařit.
Ještě jeden rekord
Týká se dalšího nedávného čínského experimentu popsaného v publikaci, v níž prvním autorem je Xing-Can Yao. Je z poloviny minulého roku a týká se propleteného stavu obsahujícího osm fotonů. Pokud neurčitost stavu, v němž se konkrétní foton nachází, přirovnáme k proslulé Schrödingerově kočce, která je zároveň mrtvá a živá, tak v tomto případě je těchto koček osm pohromadě. Pokrok v této oblasti začal v roce 1999, kdy se podařilo vytvořit propletený kvantový stav se třemi fotony. Pak se postupně počet zvyšoval až na šestici propletených fotonů.
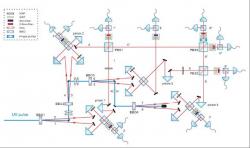
Nyní bylo možné díky už zmíněnému velmi intenzivnímu zdroji dvojic fotonů v propleteném kvantovém stavu dosáhnout propleteného stavu osmi fotonů. Velmi vysoká intenzita je nutná kvůli tomu, že v téměř stejném časovém okamžiku je třeba vytvořit pomocí čtyř nelineárních BBO krystalů čtyři dvojice fotonů v propleteném kvantovém stavu. Ty se pak pomocí speciálního interferometru spojí do propleteného kvantového stavu osmi fotonů. Laser v ultrafialové oblasti s vlnovou délkou 390 nm vytvářel pulz délky 120 fs s opakovací frekvencí 76 MHz. Velkou výzvou je dokonalá časová synchronizace vytváření čtyř dvojic fotonů v propleteném stavu. I při zmíněné vysoké intenzitě a frekvenci se za hodinu dařilo vytvářet pouze zhruba devět skupin zmíněných osmi fotonů v propleteném kvantovém stavu. Jednoduchá nebyla ani analýza a potvrzení jejich vzniku. K tomu se dospělo až určením polarizace každého z fotonů. Studium takových stavů je důležité nejen z pohledu základního výzkumu vlastností kvantového světa, ale je také důležitým krokem ke kvantovým výpočtům a počítačům.

Závěr
I ze srovnání současného stavu s tím, který byl popsán v předchozím článku zhruba před dvěma roky, je vidět, že nejen v oblasti kvantové teleportace dochází k rychlému pokroku. Zlepšuje se efektivita produkce propletených kvantových stavů i jejich přenosu na stále větší vzdálenosti. Daří se také provádět stále komplikovanější operace na stále složitějších kvantových systémech. Zatím všechny experimenty potvrzují platnost kvantové fyziky a umožňují stále podrobněji studovat její fundamentální vlastnosti i dotýkat se jejich filosofické interpretace. Navíc se stále více blížíme praktickému využití těchto vlastností v kvantové kryptografii i kvantových počítačích a výpočtech.
Pokrok v oblasti kvantové fyziky je postaven na průmyslovém a technologickém zázemí. Na jeho rozvoj se Čína již delší dobu zaměřuje, a proto není překvapením, že se do role lídra propracovává jak v oblasti teorie, tak i praxe, což dokládají její úspěchy v jaderné energetice, výzkumu neutrin, geneticky modifikovaných organismů,… Svědčí o tom i právě probíhající let tříčlenné posádky čínských kosmonautů k předem vyslanému modulu, předstupni stálé kosmické stanice. Evropa má zatím ještě v některých oblastech předstih, ale ten díky odklonu od racionality, vědy a techniky směrem k iracionalitě a mystice, rychle ztrácí. Bohužel si hodně lidí neuvědomuje, že vysoká životní úroveň a sociální zabezpečení jsou dány právě úrovní vědy, techniky a průmyslu.
Příslušné originální články jsou zde, zde a zde. Popularizovány byly nejen na serveru PhysOrg. Doporučení hodna je i přednáška Antona Zeilingera o kvantové fyzice a hlavně kvantové teleportaci. Mimo jiné je v ní názorně vysvětleno, jak se odliší, jestli výsledek měření je dán teprve tímto aktem, nebo už byl determinován předtím (popsáno pomocí barev kostek skrytých pod sousedními kyblíčky - zda byly definovány před jejich odkrytím nebo „vznikly“ až při odkrývání).
Diskuze:
Cisla a jejich logika.
Vaclav Knowledge-integration,2012-07-05 00:56:40
"Ked mám prirodzenú jednotku a odpocítam 2 bez existencie záporných císiel dostanem neplatný výsledok. Vôbec to neznamená, že "musí" existovat nejaké záporné ciníslo. Ja "chcem" aby bolo, tak také vytvorím. Záporné císla by nemuseli byt, keby sme ich nepotrebovali. "
---
S tim plne souhlasim. Zaporna cisla vytvoril nekdo, kdo dostal ten 'neplatný výsledok' a nebyl s tim spokojeny protoze byl genius a myslel, ze by melo byt mozne a prakticke nejaky vysledek obdrzet. Zrejme pri tom hrala roli nejaka prakticka motivace ze zivota (jak vyse napsal Ondrej Adamovský: záporná císla se zacala objevovat predevším s rozvojem obchodování. Bylo treba nejak rozlišit má dáti a dal.)
=========
"Bud byla k puvodne kladným císlum pridána záporná, nebo byla puvodne prirozená císla rozšírena o jeden atribut s dvema možnými hodnotami. "
---
Ta druha moznost se blizi pravde, ale ne uplne. Ten nespokojeny genius mudroval a tento problem si napsal v zakladnim tvaru jako 0-1=x protoze vsechno odecitani vetsiho od mensiho cisla se da na tento tvar zredukovat. Cili pro nazornost, 10-20=0-10 cili vzdy skoncime s vyrazem tvaru 0-n=x kde x je neznama velicina, nas hledany vysledek.
Nas genius dumal a dumal a pak se prastil do cela. Uvedomil si totiz, ze neni treba na toto odecitani vetsiho cisla od mensiho znat odpoved (protoze neni mozne mit 'mene nez nic' a tak odpoved ani nemuze existovat), ale ze plne postacuje vzit zadani problemu sameho jako odpoved na nej. A zapsal si to takhle: 0-1=0-1 anebo vseobecne 0-n=(0-n)
A dal si tento 'vysledek' do zavorky, aby bylo jasne, ze se jedna o 'vysledek' a nikoli o operaci odecitani.
No reknete, neni to genialni tah? On se to zadani vubec nesnazil resit, podobne jako nemusime resit a dodnes neresime druhou odmocninu cisla 2 (neda se presne vyjadrit v decimalni podobe vysledku), ale proste s nim pocital ve forme puvodniho zapisu problemu, jako se to obvykle cini s tou druhou odmocninou cisla 2.
Tady se zrejme jedna o zcela novy typ cisel, presneji o stara znama prirozena cisla v novem kabate. A aby byl ciselny system konsistentni, tedy aby vsechna cisla mela stejnou formu jako tato nova forma, zavedl ten nas genius pro ten stary znamy typ vysledku skladajici se z prirozenych cisel tu samou formu, ale s opacnym znamenkem, tedy takto: (0+n)
Prirozena cisla jsou takto transformovana do dvou novych sad cisel. Jedna sada jsou cisla vetsi nez nula, (0+n) a ta druha cisla mensi nez nula, (0-n). A s temito sadami cisel jsme ted schopni pocitat jako predtim, ale s tou zmenou, ze nyni dokazeme odecitat i vetsi cislo od mensiho.
A protoze to nove cislo ktere predstavuje operaci odcitani od nuly (0-n)=? nema coby pocetni operace zadny vysledek, cili jinymi slovy, vysledek teto operace je negativni (ve smyslu ze nevrati vysledek), budeme tato cisla nazyvat negativni cisla (zaporna cisla). A ta druha cisla budeme nazyvat pozitivni (ve smyslu ze vrati vysledek), kladna cisla, protoze pro operace kterou reprezentuji lze nalezt reseni v prirozenych cislech , (0+n)=n.
Po nejakem case pouzivani techto cisel z duvodu prakticnosti zapisu prestaneme pouzivat ty zavorky spolecne s nulou a piseme jen +n, -n s tim, ze tyto nepouzivane casti cisel se 'rozumi', i kdyz je nepiseme. A aby to vsechno bylo jeste prakticejsi, muzeme dokonce prestat zapisovat i to znamenko plus, protoze kladna cisla prece maji reseni v cislech prirozenych. Muzeme proto v nasich zapisech vypocetnich operacich pouzivat primo tyto vysledky, tedy cisla prirozena. V pripade cisel zapornych znamenko minus prestat pouzivat nemuzeme, protoze operace odcitani od nuly nema zadne reseni, ktere by slo pouzit namisto zapisu te operace. U zapornych cisel je maximum uspornosti a prakticnosti zapisu jiz plne dosazeno jejich tvarem -n.
---
A zde mame odpoved na otazku zda prirozena cisla jsou kladna cisla. A odpoved zni, ze nejsou.
Prirozena cisla nejsou kladna cisla, ale jak bylo uvedeno, jsou resenim operace kladneho cisla - cili kladne cislo (0+ n), ktere mimochodem samo je souctem nuly a prirozeneho cisla, ma jako reseni prirozene cislo n. A je mozne psat jak +n, tak pouze n, ale to vubec neznamena, ze n je kladne cislo, tedy ze prirozena cisla jsou kladna cisla. K takovemu omylu jsou ovsem prirozene svedeni ti, kteri nerozumi logickemu procesu vzniku zapornych a kladnych cisel. Coz je ovsem nezastavi aby neprednaseli v nasich skolach a necinili mylne zapisy ve Wikipedii.
---
Nedelam si zadny patent na vyklad nejake skutecne historie. Historicky vznik zapornych a kladnych cisel nejspis, nebo skoro urcite sel nejakou jinou, vice nebo mene klikatou cestou, nektere kroky vyse uvedene mohly byt preskoceny, nebo nebyly pro historii zaznamenany. Je dokonce mozne, ze vsechny byly preskoceny nejakou vzacnou inspiraci, i to se v matematice stava. Nicmene verim, ze vyse popsany postup vzniku techto cisel je logicky spravny a vysvetluje mnohe nejasnosti v tomto smeru doposud casto panujici.
====================================
"žiadne císla, akokolvek prirodzené sa Vám zdajú, v prírode de-facto neexistujú. "
---
Snad jsem nic takoveho netvrdil. To je jen vas nespravny vyklad toho co jsem rekl.
Prirozena cisla jsou (samozrejme) abstraktni pojmy, vytvorene lidskou mysli, na zaklade pozorovani skutecnosti, ve ktere zijeme. Zvirata, protoze nejsou schopna abstrakce vytvaret, zadna prirozena cisla neznaji - ta totiz jak spravne uvadite v prirode nijak neexistuji. Ale existuji v ni entity, veci, ktere my lide pozorujeme a odvodime si na zaklade toho pozorovani soustavu pojmu, kterymi kvantitativne tyto veci oznacujeme. Zvire vidi na louce strom jako my lide, ale jen my lide, s nasi abstraktni pojmovou vybavou, ten strom muzeme oznacit jako 'jeden strom'. Pro zvire je to proste vzdycky jen strom, tecka.
Prirozena se temto cislum rika nikoli proto, ze existuji prirozene, samy od sebe, nezavisle na cloveku (jeho mysli), ale protoze jen tato cisla maji primy zaklad v realite. Cili cislo jedna muze znamenat jeden kamen, cislo dva pak dva kameny atd. atd. Muzeme tedy primo a nazorne poukazat na nejake veci v prirode a rici - tohle mam na mysli, kdyz reknu takove a takove cislo (ale nechytejte me za slovo a nepozadujte po me, jak se tohle dela v pripade vysokych cisel, ta uz jsou generovana podle pravidel ciselne rady).
Tahle prima souvislost cisel s fyzickymi protejsky v prirode nas vedla k nazvu prirozena cisla. Jinak by se dalo taky rikat treba 'prvotni cisla', nebo neco takoveho.
Vsechna ostatni cisla, upravena treba do podoby tech zapornych a kladnych cisel uz jsou vyssimi abstrakcemi lidske mysli a nemaji jiz primou souvislost s necim fyzicky existujicim v prirode (tu maji jen ta prirozena cisla). Cili v prirode neni zaporny nebo kladny pocet kamenu, kameny nejsou ani kladne ani zaporne, v kosiku nemam kladny nebo zaporny pocet hub, baca nepase kladny pocet ovci, atd atd., proste prirozena cisla nejsou kladna a jsou lidskou invenci, ovsem invenci zalozenou na primem pozorovani sveta kolem nas.
------------------------------------------------------------
Problem je v tom dnesnim tak rozsirenem pohrdani filozofii jako takovu, ktere je ovsem pomylene, stejne jako je pomyleny napriklad rasismus - vzdycky se totiz najde vyjimka potvrzujici pravidlo, tedy ze ne vsichni prislusnici nejake rasy jsou stejni, anebo ze ne vsechny filozofie si zaslouzi zatraceni.
A vsechno o cem se tu prave bavime je castecne vec prave filozofie, konkretne filozofie vedy. A kdyz se bavime o pojmech, presneji o tom vzniku pojmu prirozeneho cisla, tak to uz jsme plne na poli filozofie vedy. Porozumel byste me lepe, kdybyste se seznamil s praci Ayn Randove 'Introduction to Objectivist Epistemology', ze ktere intelektualne vychazim.
http://en.wikipedia.org/wiki/Introduction_to_Objectivist_Epistemology
Nejsem si jisty jestli vladnete Anglictinou (tahle knizka jeste v Ceskem prekladu nevysla), ale myslim ze ano (doprucil jste me prece k precteni tu Hofstadterovu knihu "Gödel, Escher, Bach: An Eternal Golden Braid"), a pan Ondrej Adamovský zrejme take. V tom pripade bych vam (a nejen vam) mohl nabidnout k precteni co jsem pred lety napsal prave na tema o kterem je tu rec - o cislech, vcetne tech imaginarnich.
Napsal jsem to pred nejakymi skoro patnacti lety, mel jsem to tenkrat asi rok vyvesene na internetu ale pak webovy hostitel tech stranek skoncil a tak jsem to strcil 'do supliku'. Mam v planu ty stranky obnovit a dat na ne mimo jine tuhle praci. Taky bych se rad pokusil o preklad do Cestiny, snad bych to zvladnul. Zkusim nejdriv pozmenit v pdf souboru par udaju, jako treba email a podobne zastarale udaje.
----------------------
Omlouvam se za zpozdilou odpoved, dohledani a upraveni bylo narocnejsi nez jsem si predstavoval. Omluvte pripadne nedostatky v pdf souboru, hlavne nektere matematicke vyrazy nejsou uplne jak by mely byt, myslim ze puvodne jsem ho dal dohromady na Macovi a ted mam na PC problem pri upravovani s kompatibilitou. Ono vubec upravovat pdf soubory je skoro vzdy ozehava zalezitost.
http://www.mediafire.com/file/w0wy8kbwi8eef6b/complex_2012.pdf
Tak ted jsem zase spatne zaradil ja
Vaclav Knowledge-integration,2012-07-05 00:59:45
Ma to byt odpoved na komentar -> Marek Fucila 30.06.2012 v 03:02
"...
Pán Vaclav Knowledge-integration, opakovane to tu bolo spomenuté, a váš problém nie je ani tak v chápaní imaginárnych čísiel ako v pochopení súvislosti teórie čísiel a teórie množín."
se ovšem žádný takový přenašeč neuvažuje
Z Z,2012-07-02 01:53:58
No a ako sa teda teda to fyzikálne pôsobenie prenáša - bez prenášateľa? A ak sa prenesenie informácie rýchlejšie ako svetlom kvantovými javmi podarí spraviť, čo také sa výrazne zmení? Predsa ak sa dôsledok prejaví až po príčine, aj keď rýchlejšie ako svetlo, tak bude stále dôsledok po príčine a nie naopak, tak aké paradoxy?
Lokálnosť
Z Z,2012-06-28 21:33:25
Čo ak nie je kvantová mechanika "nelokálna", ale sa zmeny "vlnovej funkcie" menia rýchlejšie ako svetlo? Alebo dogma o nemožnosti šírenia informácie rýchlejšie ako svetlo? Čo ak sa také niečo podarí? Tvrdenie, že kvantové javy umožňujú fyzikálne ovplyvniť niečo rýchlejšie ako svetlo, no tak, aby sa nedala preniesť hocijaká informácia, sa mi zdá ako snaha ponechať pravdivosť dvoch vzájomne si odporujúcich teórií.
Šíření informace
Pavel Bílek,2012-06-30 02:09:47
Šíření informace rychleji než světlo patrně neumožňuje vznik žádného paradoxu za podmínky, že jak pro vysílajícího, tak pro přijímajícího platí, že napřed došlo k události vyslání a až potom k události přijetí informace. Z hlediska teorie relativity by byl problematický nějaký přenašeč informace pohybující se rychleji než světlo, při kolapsu vlnové funkce se ovšem žádný takový přenašeč neuvažuje. Blíže k tomu viz kapitolu Kauzalita na http://www.quantum-mechanics.eu/czech.html
Při kolapsu vlnové funkce nemusí být zřejmé, kde došlo k prvnímu měření. Když se dva majitelé propletených částic pohybují směrem k sobě a zároveň (z pohledu "nepohybujícího se" pozorovatele) provedou měření svých částic, tak pro oba měřitele platí, že měření napřed provedl ten druhý z nich. Když se naopak pohybují od sebe, tak jeden stejně jako druhý provedl měření dřív než ten druhý.
Re: Šíření informace
Pavel Bílek,2016-08-19 17:42:15
Oprava:
Paradox může nastat i v případě, kdy jak pro vysílajícího A, tak pro přijímajícího B platí, že napřed došlo k události vyslání a až potom k události přijetí informace. Mějme vysílajícího C a přijímajícího D ve vztažné soustavě, která se pohybuje ve směru od stanoviště A ke stanovišti B, takže v ní došlo napřed k přijetí u B a až pak k vyslání u A. Poté, co B přijme informaci od A, předá ji kolmo kolem prolétajícímu C, ten ji přepošle příjemci D, který se vůči němu nepohybuje a který v okamžiku jejího přijetí prolétá kolem A, kterého kolmo informuje, že odeslal informaci ještě předtím, než ji odeslal, což je paradox.
Rozporuplne jevy
Vaclav Knowledge-integration,2012-07-10 13:39:19
Z Z, klade spravne otazky, anebo kdyz to nejsou otazky, je to dobry podnet k zamysleni.
K tomu co napsal Pavel Bilek bych rekl, nebo dodal, ze kauzalita je vec fyziky, tedy vec realnych pochodu. To znamena, ze ve skutecnosti kauzalita musi byt vzdy a za vsech okolnosti platna, tecka (podobne jako zachovavani energie). To dale znamena, ze pokud by nase vedecke teorie rikaly neco jineho, byly by dozajista spatne zkonstruovane (anebo to co nam rikaji si nespravne vykladame) a meli bysme se zajimat o to, jak je zmenit, aby neco takoveho protireciciho z nich nevyplyvalo.
Takze naprosto neni treba ani na to neni na miste abychom meli nejake obavy z moznych budoucich objevu jak ten nas svet funguje. Pokud z nejakeho objevu bude vyplyvat neco neslucitelneho s nasimi stavajici teoriemi, pak se proste musime vratit zpet do svych vedeckych pracoven a kajut a hledat, kde jsme udelali chybu, protoze realita z definice paradoxy neobsahuje (a poruseni kauzalniho retezce by paradoxem jednoznacne bylo). Tim si muzeme byt naprosto jisti. Samozrejme, nejen teorie ale i samotne experimenty muzou byt chybne a je treba je v pripade pochyb opakovat, dokud si jejich vysledky nejsme alespon nejak rozumne jisti.
Dnesni obavy z toho, ze by se treba naslo neco, co by umoznilo prenos neceho fyzickeho rychleji nez se pohybuje EM zareni (i prenos abstraktnich, tedy nehmotnych 'informaci' vyzaduje prenos nejake fyzikalni zmeny kterou je jejich prenos sireny) jsou hlavne obavy ze zhrouceni nasich stavajicich teoriich, ktere by potom bylo nutne nejak upravit, aby to vzaly v potaz. A na neco takoveho naprosta vetsina vedecke komunity samozrejme neni pripravena, protoze vedu postrkuje dopredu prave jen nejaka jeji miziva cast, zatimco vetsina dokaze jen prihlizet a popripade rozvijet nove nalezene. A je logicke, ze vetsina vedcu bude mit obavy z mozneho sesazeni stavajicich teorii, mozneho noveho zamichani karet, protoze jsou si dobre vedomi, ze sami by je nebyli schopni nejakymi jinymi nahradit, popripade ty rozbite 'spravit'.
---
V souvislosti s moznosti sireni neceho rychleji nez EM zareni bych podotknul, ze dnesni fyzicke procesy, o kterych vime ze se siri rychlosti svetla, se po nejakem objevu neceho siriciho se rychleji nebudou najednou sirit rychleji, ale budou se i nadale sirit maximalne rychlosti svetla jako doposud. Cili stavajici procesy nebudou nejak sesazeny ze sveho rychlostniho trunu a posazeny na nejaky rychlejsi. Objev neceho takoveho by jen znamenal rozsireni stavajici fyziky a to nutne nekonfliktni rozsireni, pokud predpokladame spravny vyklad toho noveho jevu.
-----------------------
"Z Z: Tvrdenie, že kvantové javy umožnujú fyzikálne ovplyvnit nieco rýchlejšie ako svetlo, no tak, aby sa nedala preniest hocijaká informácia, sa mi zdá ako snaha ponechat pravdivost dvoch vzájomne si odporujúcich teórií."
--
Tady se snad da rict jedine - ze dokud nerozumime zakladnim jevum kvantove mechaniky, neni mozne vynaset zadne soudy. Vsechno je stale otevrene. Proste nevime proti cemu jsme postaveni a tak se nam muzou veci jevit jako rozporuplne.
zaujímavý článok
Maroš Štulajter,2012-06-28 11:20:37
je to veľmi zaujímavý článok. musím sa ale priznať že kým som pochopil o čo sa jedná tak som musel prečítať viac článkov. článok bol napísaný príliš odborne, napr. (kolaps vlnovej funkcie, ale v skutočnosti je to logické. musím ale vytknúť čo tam nebolo napísané. nebola tam popísaná schéma optickej zostavy. veľmi by to zjednodušilo obsah článku. vcelku dobrý článok, ale málo technických údajov.
logika, aritmetika ani geometre není jenom jedna
Ondřej Adamovský,2012-06-27 22:28:43
Zdaleka ne všechnu matematiku, kterou kdy kdo objevil, objevil pozorováním světa kolem sebe. Od dob starých řeků bylo prozkoumáno mnoho různých aritmetik, logik, i geometrií. Ostatně to je dobrá metoda zkoumání systému axiomů, když jeden z nich nahradíme jiným, který je s tím původním v rozporu, můžeme na základě zkoumání výsledku lépe poznat význam toho původního axiomu. Může se nám podařit systém zobecnit a původního axiomu se úplně zbavit. Nebo můžeme zjistit, že onen nový systém je zajímavý, nebo krásný, a pokračovat v jeho rozvíjení jenom z čiré radosti z poznávání, a kdo ví, třeba se nakonec ukáže, že se to i k něčemu praktickému hodí.
Samozřejmě, že se na základní škole učíme tu logiku/aritmetiku/geometrii, kterou lze dobře aplikovat na náš svět, jakou jinou bychom se tam taky měli učit. Ta otázka zní, čím je tato "praktická" logika/aritmetika/geometrie jiná od těch ostatních. Pro mne je odpovědí to prosté pozorování, že na náš svět je aplikovatelná ona, a ty ostatní ne, nebo hůř. Vy, jak vyvozuji z vaší touhy po nějakém "vysvětlení" byste se s tím ale spokojit neměl.
Ondřej Adamovský,2012-06-28 07:49:42
(reakce na "Protoze svet je takovy a ne jiny" od Vaclav Knowledge-integration v následujícím vlákně)
To jste si nespravne vylozil co jsem tim minil
Vaclav Knowledge-integration,2012-06-29 10:57:29
Pisete ze "Zdaleka ne všechnu matematiku, kterou kdy kdo objevil, objevil pozorováním sveta kolem sebe."
Tim pozorovanim sveta kolem sebe to jen zacina. Clovek tak ziska jen zakladni pojmy, na kterych pak stavi abstraktni 'zamky' uvnitr sve mysli.
My se tak trochu mijime, myslel jsem to pozorovani sveta na trosku hlubsi urovni. Nejdriv jako male deti musime vubec poznat svet, a pak jako dospeli z toho poznani tezime, zamyslime se nad tim svetem a zalozime novou disciplinu jako treba Euklid geometrii, nebo Aristoteles logiku... A pak je mozne pro dalsi myslitele aby tyto zaklady dal rozvijeli, staveli na nich, ale uz nepotrebuji vzdycky pozorovat svet kolem sebe, mohou tu zakladni teorii rozvinout abstraktne, jen musi davat pozor, aby jejich vytvory byly v souladu s tou zakladni vedou (a ovsem taky porad kontrolovat sve vyvody experimentalne, pokud je to mozne, nebo patricne).
Pokud neudelaji chybu, pak se nemusi nikdy podivovat, jak to ze jejich veda tak zazracne v tomto svete funguje, je na tento svet aplikovatelna. Tak se divi jen ti, kteri se nikdy nenaucili zaklady sveho remesla. Dalo by se to prirovnat k ve meste vyrostlym detim, ktere si treba mysli, ze mleko pochazi ze supermarketu, anzto kravu nikdy nevidely. Je to smutne, ze nasi 'predni vedci', uznavane autority jsou vskutku v podobne pozici, pozici papousku, kteri nerozumi zakladum sve vedy.
------------------------
V tom druhem odstavci se priznam ze me neni jasne jak jste dosel k tomuto zaveru: "Vy, jak vyvozuji z vaší touhy po nejakém "vysvetlení" byste se s tím ale spokojit nemel."
Prece kdyz znam zaklady tech disciplin, jak prirozene vyrustaji z faktu sveta, pak te jejich aplikovatelnosti na tento svet tim padem rozumim a mam to nejlepsi vysvetleni. Kdezto u vas je to tak, ze vy se zrejme spokojite s prostym slepym pozorovanim, ze jsou aplikovatelne, aniz rozumite tomu, proc to tak je. Proste pro vas jsou aplikovatelne a hotovo, smytec.
Ja ovsem na rozdil od vas vidim proc aplikovatelne jsou a zadne dalsi hlubsi vysvetleni nepotrebuji.
"záhada" imaginární jednotky
Ondřej Adamovský,2012-06-26 19:42:16
Stejnou "záhadou" jako imaginární jednotka i je v matematice znaménko mínus. Jakto, že to funguje, když jej přidáme ke kladnému číslu, dostaneme odpovídající záporné. Nad touto "záhadou" se nikdo nepozastavuje. Nejspíš je to proto, že se zápornými čísly se v životě běžně setkáváme. Myslím, že jedinou záhadou imaginární jednotky i je to, že, stejně jako to ve svém příspěvku o kvantově mechanické hračce popisuje pan Brož, pro žáky ve školách je to zcela nový koncept, se kterým se dosud nesetkali, ba naopak se dříve učili, že odmocňovat záporné číslo se nedá.
Matematici se vždycky potýkali s tím, že nějaká množina není uzavřená na nějakou operaci (například množina kladných čísel není uzavřená na operaci odečítání, protože pokud odečteme větší číslo od menšího, kladné číslo nedostaneme). Rozšíření kladných čísel na celá uzavřelo množinu na odečítání. Další rozšíření na racionální čísla tuto množinu téměř (s výjimkou dělení nulou) uzavřelo dělení. Bylo jen přirozené, že si nějaký matematik řekl, co by se asi stalo, kdybych měl číslo, jehož druhá mocnina je -1. A řekl si, dobře, řekněme, že ho mám a označíme ho i. Zkoumal, co by to znamenalo, jaké zákonitosti by z toho vyplynuly, případně jestli by to náhodou nevedlo ke sporu. A ejhle, dávalo to smysl, a objevila se komplexní čísla. Čili otázka, jaktože to funguje, jaktože i*i=-1, je poněkud hloupá, když jediná základní výchozí kvalita čísla i je právě takto definovaná.
Samozřejmě, mohli bychom se ptát, proč to nevedlo ke sporu, jaktože takhle definované i není nesmysl. Matematika ovšem zkoumá vztahy předem definovaných objektů pomocí předem definovaných logických pravidel, takže na určité úrovni můžeme to, že takto definované i "funguje", považovat za vyzkoumaný výsledek matematiky. Na vyšší úrovni navíc matematika zkoumá i jak jak se liší matematické systémy používající různých logických pravidel a různě definovaných objektů, tkže i na tyto otázky matematika odpovědi hledá. Matematikovi stačí se rozhodnout, na které úrovni se při řešení dané úlohy zastaví, na nějaké musí, protože zkoumání jedné úrovně matematiky vždy vyžaduje úroveň vyšší, ještě abstraktnější přístup.
Dál mne napadá už jen jediná otázka, a to proč je počítání s i tak prakticky použitelné v našem světě, ale to je obecná otázka ohledně celé matematiky, neboli proč je v našem fyzickém světě použitelná právě ta naše aritmetika, logika, geometrie, atd., jak se ji učíme na základní škole, a ne nějaká jiná, s jinými pravidly. Tedy tato otázka by mohla znít třeba "Proč jsou jedno jablko a jedno jablko dvě jablka a ne třeba tři jablka?". Takovéto otázky je myslím tak nanejvíš zajímavé si uvědomit, že by je snad možná mohl někdo položit, ale dělat se s nimi nic moc nedá. Každopádně to není otázka pro matematika.
Ondřej Adamovský,2012-06-26 19:43:11
mělo být k vláknu pana Brože "ad p. Vaclav Knowledge-integration"
myslím si totéž
Pavel Brož,2012-06-26 20:25:19
Stejně jak Vy si myslím, že hloubáním nad "záhadou" imaginární jednotky se k žádné "hlubší pravdě" dobrat nelze - ledaže by to byl speciální druh pravda, tzv. Velká Pravda, která se pozná podle toho, že její logická negace je také Velká Pravda.
Na světě je přitom tolik opravdu zajímavých a záhadných problémů.
1+1=2
Marek Fucila,2012-06-27 03:05:01
Ja by som tú záhadu videl ešte posunutú ďalej. Myslím si, že matematika ako chápanie sveta je nejakým "odrazom" fyzického prostredia vo vrodenej štruktúre mozgu. U nejakých mimozemšťanov by možno mohla byť iná, ale človek zo svojho "tieňa" nevystúpi a chápanie "jeden plus jeden je viac ako jeden" je proste v nás. Sú nejaké dôkazy o tom, že takéto základy matematiky majú aj nižšie postavené živočíchy. Myslím si teda, že počítanie je intuitívne, a že človek má navyše tú schopnosť uvedomiť si, že počíta. Na tom potom vznikla matematika akú ju poznáme (alebo skôr matematici, ja som laik:-)).
No a tá záhada pre mňa spočíva v tom, ako je možné, že z užitočnej schopnosti určiť čo je viac a čo menej (počítanie) zrejme skombinovanej so schopnosťou "riešiť problémy" (vrodená inteligencia) sme dokázali ako ľudstvo dospieť tak ďaleko v pochopení sveta, a kde ležia tie hranice chápania. Myslím si, že celý problém pána Vaclava Knowledge-integration je v tom, že mu nestačia odpovede na otázky "ako to funguje" ale hľadá v tom nejakú estetiku. Snaží sa vykročiť zo svojho tieňa a odmieta akceptovať to, že tie hranice chápania máme aj pri základných otázkach. Filozofovať sa dá nad hocičím, ale snaha pochopiť "pochopené" je len snahou o posun svojej predstavivosti za svoje hranice. K super príkladom z teórie čísel, ktoré dokazujú tvrdenie Pavla Broža, že ľudia berú za samozrejmé až tie veci, ktoré sa dozvedeli už v detstve, pridávam príklad neschopnosti predstaviť si štvrtý priestorový rozmer. Sú fyzikálne teórie, ktoré operujú s väčším počtom rozmerov, a možno je niektorá z nich pravdivá. Aj ak sa to niekedy dokáže, stále si ľudia nebudú vedieť predstaviť viac ako 3 rozmery, stále neuvidia v košíku imaginárny počet jabĺk, rovnako ako ani záporný, a stále budú mať možnosť hľadať perpetum mobile a obviňovať vedu, že im kladie prekážky. Každopádne ak nejde len o filozofický vzdor, ale premieta sa to do reálnej činnosti vytvoriť alternatívnu teóriu, úspech sa apriori nedá vylúčiť.:-)
Protoze svet je takovy a ne jiny
Vaclav Knowledge-integration,2012-06-27 13:10:15
"proc je v našem fyzickém svete použitelná práve ta naše aritmetika, logika, geometrie, atd., jak se ji ucíme na základní škole, a ne nejaká jiná, s jinými pravidly."
To co se ucime na zakladni skole nekdo nekdy v minulosti nejak objevil. A objevil to pozorovanim sveta do ktereho se narodil. Zaklady aritmetiky, logiky, geometrie, jsou vsechny odvozeny z pozorovani tohoto sveta. A proto je logicke, ze ta aritmetika, logika, geometrie (i kdyz tyto mohou byt dale vypracovane vice do hloubky uz samy o sobe bez primeho odpozorovavani skutecnosti, ovsem vypracovane v souladu s temi fakty, ktera ze skutecnosti odpozorovana byla), jsou zpetne aplikovatelne na tento svet.
Zakladni logicke pravdy byly ve starem Recku odkoukane od prirody. Tehdejsi filozofove si sedli a zadumali se nad svetem ve kterem se nachazi a objevili v nem jiste zakonitosti, ktere pozdeji jiny filozof (Aristoteles) sesumiroval do konecne podoby pravidel logiky (je mozne ze sam Aristoteles na ne prisel, ale to je vec historickych faktu, na principu veci to nic nemeni).
-----------
"Každopádne to není otázka pro matematika."
Mozna jste si vedom, ze se rika, ze filozofie je matkou vsech ved. Prakticky to znamena, ze pokud hloubame pobliz zakladu jakekoli vedy, narazime tam na otazky filozofickeho druhu. Proto kazdy vedec, pokud nechce byt jen sroubkem, ci koleckem s soukoli vedy, pouze prenasejici dosazene vedecke poznani pristim generacim, mel by se o tyto otazky zajimat. Neni vubec nahodou, ze vsichni velci vedci byli take do jiste miry filozofove. Kladli si a hledali odpovedi na filozoficke otazky sveho oboru a jejich filozoficke nazory byly casto odrazovym mustkem k jejich objevum. Proste byli o necem hluboce presvedceni a to je nakonec dovedlo k objevum. Nekdy ovsem, kdyz je to presvedceni mylne, vede k omylum. Napriklad Einsteinovo presvedceni, ze Buh nehraje kostky... (Ovsem nehodnotil bych to osobne tak prikre jako omyl, aspon dokud nebude jasno o jakou hru vlastne jde - zrejme se nejedna o prosty hazard.)
Badani nad mravencem muze vest k pochopeni slona
Vaclav Knowledge-integration,2012-06-27 13:19:47
Pavel Brož: "Na svete je pritom tolik opravdu zajímavých a záhadných problému."
---
Ale jiste jste si vedom toho, ze plno velkych, tech opravdu zajimavych a zahadnych problemu, bylo vyreseno jako nasledek reseni malych problemu, kterych si malokdo vsimnul, protoze byly malo zahadne, zajimave. Feynman byl ukazkovym prikladem jak prvotni zajem o uplne prkotiny do nakonec dovedl k Nobelove cene v primem retezci pricin a nasledku, jak jej sam nekde popsal.
ad p. Vaclav Knowledge-integration
Pavel Brož,2012-06-28 00:18:29
Víte, nezlobte se na mě, ale s tím Feynmanem jste úplně vedle. Feynman byl ve skutečnosti vyloženým protipříkladem hloubání nad takovými věcmi, jako je imaginární jednotka, a jeho vztah k filosofii byl velice dobře znám, byl mimochodem totožný, jaký měl Steven Weinberg a Stephen Hawking (doporučuji např. Weinbergovu kapitolu o nepochopitelné neefektivnosti filosofie v jeho knížce „Snění o finální teorii“). Dokonce si troufám říct, že Feynmanův vztah k neproduktivnímu hloubání byl z nich třech nejradikálnější, promítal se v celém jeho životě. Feynman se ke každému fyzikálnímu problému postavil vždycky s otázkou, co k tomu problému říká experiment, a nakolik ta která myšlenka či teorie může být vzápětí prakticky ověřena, ať už okamžitě realizovatelným měřením, anebo konfrontací se známými fyzikálními fakty.
Svého času jsem měl doma všechny takové ty populárně laděné knížky jako „To snad nemyslíte vážně, pane Feynmane“, „Snad ti nedělají hlavu cizí názory“, atd. atd.. Asi před rokem jsem udělal masakr ve své knihovně, a zredukoval ji asi na desetinu, jednoduše z toho důvodu, že jsem dospěl k závěru, že držení tolika knih je zbytečné, když už je má člověk vícekrát přečtené. Konkrétně od Feynmana jsem si ponechal jenom jeho třídílné „Feynmanovy přednášky z fyziky“, od pohledu patří k nejpoužívanějším knihám z mé knihovny. Namátkou teď jimi znovu listuji, a mohu Vás ujistit, že prakticky na každé stránce mohu doložit Feynmanův nedostižnou schopnost rychle ve svých myšlenkách odhazovat neplodný balast a neustále provádět konfrontaci všech teoretických úvah s praxí.
Není mým cílem Vás přesvědčovat, abyste změnil názor či zanevřel na filosofii a stal se pragmatikem Feynmanova střihu. Každý jsme nějaký. Lidé mající raději filosofii než fyziku dají přednost Vašemu pojetí, a naopak fyzici znající např. ony Feynmanovy přednášky v tom mají taky jasno, samozřejmě opačným způsobem. Jde mi jen o to, že prezentovat Feynmana jakožto člověka ochotného bloumat nad „problémy“ typu imaginární jednotka, je v naprostém protikladu s tím, jak on sám fyziku dělal i učil.
Obycejne veci ktere bereme jako samozrejmost.
Vaclav Knowledge-integration,2012-06-29 18:49:14
"Stejnou "záhadou" jako imaginární jednotka i je v matematice znaménko mínus. ... Nad touto "záhadou" se nikdo nepozastavuje. Nejspíš je to proto, že se zápornými císly se v živote bežne setkáváme. "
Jak to nikdo. Treba ja jsem se nad tou zahadou pozastavil a nedalo me to spat, dokud jsem si to pekne neobjasnil. A taky jsem se se zapornymi cisly v zivote pred tim uplne bezne setkaval.
Jde jen o to vystoupit ze stada, podivat se cerstve na kazdodenni okoukane veci, otazat se sebe sama, zdali jim doopravdy rozumim... tedy jestli vlastne jen nepapouskuji co se na vsech rozich (skolach) rika.
Vite, skoro vzdycky kdyz se nekdo pta genia jak na ten svuj genialni objev prisel, rekne vam typicky ze to vsechno zacalo nejakou prkotinou, kterou vsichni znaji, ale nepozastavuji se nad ni, proste protoze nejsou geniove.
Klidne se na me zlobte, ale vedle jste vy.
Vaclav Knowledge-integration,2012-06-29 19:39:54
Ja prece o tom Feynmanovi nerikam nic jineho, nez co on sam rekl o sobe, v knizkach a dokonce v rozhovorech zaznamenanych na videu. Nechame toho, at si to lidi co to tu ctou preberou sami a rozhodnou se kdo rika pravdu.
O Feynmanove opovrhovani filozofii vim a takovy postoj je ve fyzice pravidlem a vetsina (ovsem nikoli cela) filozofie takovemu postoji bohuzel zavdava pricinu. Presto vsechno ale stale plati, ze filozofie je matkou vsech ved, vcetne fyziky a ze kdyz je tato matka v upadku, budou brzy v upadku i vedy, ktere na ni zavisi. A fyzika co se tyka zakladnich teorii neni prave v nejakem obdobi prekotneho vyvoje - ten skoncil nekdy v prvni polovine minuleho stoleti a ted uz se dlouho jen dojizdi na impuls te doby.
Nevim co tu chcete naznacit tim popisem redukce vasi knihovny, snad tim nechcete poprit vse co o svem zivote ve fyzice sam autor rekl. A ten byl presne takovy jak jsem ho hodnotil - hracickar, coz ovsem neni hanlivy termin, ze ktery by se stydel, prave naopak. Nevim proc byste mu ho upiral. Zamyslel se nad vecmi, ktere ostatni povazovali za hracickarstvi, za neplodne mrhani energie na problemy, ktere jeho souputnici nepovazovali za prinosne pro vedu. Ale jemu prave to hrani s fyzikou nedulezitych jevu davalo chut delat fyziku vubec. Ale to at si lide prectou a ohodnoti sami.
Nevim vubec odkud berete to presvedceni, ze hrani si s nedulezitymi fyzickymi jevy znamena automaticky byt neproduktivni, kaslat na experimentalni potvrzovani, overovani a konfrontovani se znamymi fyzikalnimi fakty, jak to tak vzletne uvadite. Vite pane Brozi, i detska hra je velice vazna skola zivota, pokud se provozuje jak se patri.
Mozna vas urazi, ze o vasich polobozich nekdo hovori jako ja tady. Ale to je vas problem, ne muj.
-----------
Velice bych uvital pane Brozi, kdybyste se prestal opakovane vyjadrovat k me osobe, jako napriklad zde --> "Doufám, že se Vás nedotknu svým odhadem, že jste filosof, at už vzdeláním, anebo filosof, který se nejakým omylem ocitl na studiu fyziky, prípadne ji i absolvoval. To nemyslím nijak pejorativne, proste každý jsme nejaký."
Blahosklonne shlizeni na obycejne smrtelniky z olympu vedy z toho couha jako slama z bot. Pokud mate obavy, jestli se me vase komentare k me osobe nedotykaji, nedotykejte se me prosim a argumentujte k veci. Je to tak jednoduche. Dekuji.
ad p. Vaclav Knowledge-integration
Pavel Brož,2012-06-29 22:48:48
Podívejte se, ono tomu opravdu není těžké rozumět, Vy prostě z nějakého důvodu označujete množinu lidí, kteří nemají problém pochopit to, co Vy máte problém pochopit, za stádo. Budiž. Nepochybně se s Vámi shodnu v tom, že toto Vaší terminologií stádo, je velice, opravdu velice početné. Kdyby tam patřil jenom Feynman, Weinberg, Hawking, Dirac, Einstein, Poincaré, Lorentz, Maxwell, Leibnitz, Newton, ale oni to stádo tvoří kromě všech teoretických fyziků i všichni matematici a inženýři, a navíc se toto Ve Vaší terminologii stádo každý rok rozrůstá o statisíce dalších matematiků, fyziků, inženýrů. A ti všichni dohromady stádně ovládají či dokonce denně používají Moivreovu větu, větu o reziduu, konformní transformace, teorii Riemannových funkcí, analytická prodloužení, holomorfní funkce, Laurentovy řady, prostě všechny ty nesmysly postavené na komplexní algebře, aniž by přitom rozuměli imaginární jednotce.
Zaplaťpánbu, že do tohoto „stáda“ patřím…
Prinalezitost ke stadu
Vaclav Knowledge-integration,2012-06-30 10:45:06
"aniž by pritom rozumeli imaginární jednotce."
---
Provozovani vedy na te jednotce postavene prece neni nijak vazane na to jestli ji vedci rozumi nebo ne.
Opicaci taky kdyz prijdou na to, ze zmacknutim jisteho tlacitka zpusobi, ze z otvoru vyjede banan, ze zmacknutim jineho vyjede kava v kelimku, taky nemusi k ovladani tohoto a dalsich takovych tlacitek znat jako to vlastne funguje. Nevedomost jak to funguje jim vubec nebrani si takto sestavit, po nejakem tom pokusu a omylu, jidelnicek dle prani, kdykoli se jim zamane. A kdyby prece jen na ten mechanismus fungovani prisli, nijak to neovlivni tu funkcnost tlacitek sestavovani jidelnicku, jen ted budou o neco chytrejsi a treba budou schopni tu znalost toho fungovani nejak lepe vyuzivat... A podobne je to s temi komplexnimi cisly.
Dneska jeste nektere vedce trapi interpretace kvantove mechaniky, a jeste vcera to trapilo skoro vsechny. Ale zanedlouho nastupujici generace novych vedcu se s tim uz trapit nebude, prohlasi ten problem za falesny, ze zadny vlastne neni a bude to. A generace vedcu po nich uz z vysin vedeckeho olympu bude jen utrpne shlizet na ty pomylence tvrdici, ze nejake porozumeni kvantove mechanice by bylo zahodne a melo by byt mozne.
Ovsem kvantovou mechaniku a prakticke vydobytky z ni plynouci nejaky objev jeji prijatelne interpretace nijak zasadne neovlivni. Kdyz uz neco, tak to muze jen pomoci tuto oblast vedy dale rozvinout.
Plno vedcu ktere jste jmenoval a nejmenoval proste venovali sve usili ve vede jinym jejim oblastem. Opicaky by z nich ucinilo jen explicitni odmitani problemu, jeho zametani pod koberec, kdyby s nim byli explicitne konfrontovani. Kdyz si toho problemu treba i vsimnou, ale zda se jim nad jejich sily, nebo proste maji jine zajmy, tak to z nich opicaky necini, dokud ten problem nezacnou zapirat.
Veda totiz znamena hledani pravdy, hledani jak svet ve kterem zijeme funguje. A ciste pragmaticky pristup, kdy se spokojime s vyuzivanim objevenych 'tlacitek' a odmitneme se zabyvat tim, jak vlastne funguji, stavi vedu na roven opici vedy.
nepřináležitost ke "stádu" chápajících
Pavel Brož,2012-07-01 19:21:55
Dříve jsem čas od času doučoval matematiku, jen tak zadarmo čistě jen pro radost z předávání poznání. Většinou to byl nějaký kolega anebo kamarád, nebo známý kolegy či kamaráda, atd… Podle potřeby jsem doučoval středoškolskou anebo vysokoškolskou matematiku, podle toho, zda ten dotyčný plaval v přípravách na maturitu, či na přijímačky na výšku, anebo na nějakou semestrální zkoušku. Musím říct, že mnohé matematické disciplíny se opravdu nevyučují moc názorně. Nejčastěji to bývá případ vektorové geometrie, lineární algebry obecně, ovšem také názorný výklad diferenciálního a integrálního počtu bývá ve výuce kolikrát velice ošizen.
Oproti tomu třeba pochopení algebry komplexních čísel, tedy mj. i důvody pro zavedení imaginární jednotky, prakticky nikdy nepředstavovalo nějaký kámen úrazu. Narazil jsem pouze na dvě výjimky, byly to dvě dyslektičky, obě se připravovaly na maturitu, a poté chtěly absolvovat přijímačky na VŠE. V jejich případě vznikl problém s geometrickou představivostí. Bylo to úplně poprvé, co jsem se setkal s tím, že pro některé lidi může představovat nepřekonatelný problém vytvořit si v hlavě geometrický obraz zadaných charakteristik, natož s ním pak v hlavě operovat (např. představit si jej otočený, atd.). Později jsem se dozvěděl, že tento deficit je u dyslexie velice běžný; hodně lidí si myslí, že dyslexie představuje především poruchu při vyjadřování se, ve skutečnosti ale jde o mnohem komplexnější problém.
Mým nejoblíbenějším výkladem komplexních čísel byl výklad geometrický, postavený na geometrické představě Gaussovy roviny, číslech jakožto bodech na této rovině, a algebraických operacích jakožto geometrických operací skládajících se z posunutí, otočení a škálování. Jedná se o velice často používaný standardní výklad, pro úplné nematematiky jej prezentoval ve svých knížkách např. Roger Penrose, ale samozřejmě i mnozí další. Lze jej nalézt v mnoha středoškolských učebnicích matematiky (i když ne ve všech). V daném případě oněch dvou dyslektiček jsem nakonec po mnoha neúspěšných pokusech musel tuto geometrickou cestu zavrhnout a přistoupit k výkladu cestou symbolické algebry, kdy se postulují algebraická pravidla pro sčítání a násobení jistých uspořádaných dvojic, pak lze např. odvodit dělení těmito čísly, a pak se specifikují speciální případy a zjišťuje se, co tou kterou specifikací vznikne. Lehce se ukáže, že algebra uspořádaných dvojic s nulovou druhou komponentou dá již známou algebru reálných čísel, zatímco uspořádané dvojice s nulovou prvou komponentou netvoří uzavřenou podalgebru (kvůli postulovaným pravidlům pro násobení). Změnou symboliky lze potom přejít od operací nad uspořádanými dvojicemi k operacím nad neuspořádanými součty reálných a imaginárních čísel, dohromady tvořících čísla komplexní.
Ukázalo se, že tato cesta byla v případě oněch dvou dyslektiček schůdná, a že po čase neměly problém komplexní čísla bez problémů nejen používat, ale na požádání uměly i vysvětlit např. proč byla počáteční volba postulátů pro násobení oněch uspořádaných dvojic tak užitečná později. Prošel jsem s nimi i ukázkový případ, kdy ta počáteční pravidla byla zvolena obecněji, aby se na něm ukázalo, že požadavky na tu algebru kladené (asociativita a komutativita násobení a jednoznačná dělitelnost) si samy vynutí volbu těch pravidel, jaká byla na začátku postulována.
Obě ženy po skončení doučování absolvovaly úspěšně maturitu a jedna i přijímačky na VŠE (ta druhá se vdala a na VŠE se přihlásila a byla přijata až o pár let později). Tímto chci dokladovat, že pochopit imaginární jednotku dokážou i dyslektici, přestože to při svém handicapu nemají jednoduché. Zmíněné dvě dyslektičky potřebovaly moji pomoc, ale jsou známí i dyslektici, kteří se později stali velice dobrými matematiky, a kteří si museli pochopení komplexní algebry nalézt sami.
Neříkám, že každý, kdo se setká na střední škole s komplexní algebrou, tak si pro ni automaticky vytvoří pochopení. Většina studentů opravdu nemá důvod či motivaci nad tím přemýšlet, je to jenom jedna z mnoha věcí, které se musí naučit, jelikož jsou vyučujícími vyžadovány. Nicméně na rozdíl např. od pokročilejších matematických disciplín nejde v případě komplexních čísel o žádné nepřekročitelné tajemno; každý, kdo je jen maličko matematicky talentovaný a netrpí nějakým handicapem typu zrovna té dyslexie, tak si s tímto tématem umí poradit vlastními silami během maximálně pár hodin samostatného hraní si s těmi čísly. Drtivá většina těchto matematicky aspoň trochu zdatných (tj. např. ne vyloženě antitalentovaných) studentů potřebuje jakožto hlavní vstupní ideu pouze tu Gaussovu rovinu plus představu komplexních čísel jakožto bodů na ní, což je nejstandardnější způsob výuky komplexní algebry. A nikdo z nich, jakmile tu komplexní algebru zvládnou, by už nikdy nadále nepovažoval imaginární jednotku za něco záhadného a dodnes nedostatečně vysvětleného, podobně jako nepovažují za záhadná záporná čísla, nulu, nebo odmocninu ze dvou.
Stejně tak třeba zmiňovaný Feynman opravdu neměl problém s pochopením imaginární jednotky. Feynman nebyl dyslektik ani to nebyl matematický antitalent, a imaginární jednotku dokázal beze zbytku pochopit sám, jednoduše proto, že pochopit ji jde vícero ekvivalentními cestami, a žádná z nich není nikterak obtížná; samozřejmě, pokud někdo jak se říká na tu byť jen středoškolskou matematiku „nemá buňky“, no tak to pak pro něj může být celoživotní záhada, ta imaginární jednotka.
Psychologicke nemoce nechme stranou. Dekuji.
Vaclav Knowledge-integration,2012-07-04 11:50:41
"Feynman nebyl dyslektik ani to nebyl matematický antitalent"
Ujistuji vas, ze tady problem hledat nemusite. Pro me plati to same. Jsem uplne psychologicky zdravy a antitalent taky urcite nejsem, ze to musim rici sam.
A z vaseho popisu je zrejme, ze vy stale nechapete o jakem porozumeni, o jakem pochopenim tu pisu - to nema nic co delat s pochopenim manipulace imaginarni jednotky a jeji nasledne pouzivani ve vyssi analyze complexnich cisel. Jde me o vysvetleni postulatu imaginarniho cisla jako takoveho.
A neprijimam nejake odbyti skupinami, mnozinami cisel a podobnym vatovym balastem moderni matematiky. Rovnez geometricke vysvetlovani pomoci grafu, nebo pomoci tech vami zminenych matic (aspon se domnivam ze to jste mel na mysli) nevysvetluje podstatu imaginarniho cisla.
----
"podobne jako nepovažují za záhadná záporná císla, nulu, nebo odmocninu ze dvou"
Co kdo povazuje za zahadne, nevysvetlene zalezi na tom, jak to kdo ma v hlave usporadane, takze kdy neco nesedi, vsimne si toho, trapi ho to. V bordelu nebo v prostredi plnem mlhy, intelektualni vaty, si clovek vubec nevsimne, anebo mu nevadi, kdyz neco neni na svem miste, ale v usporadanem prostredi neco takoveho bije do oci. Vzdycky jen miziva cast vedcu se pozastavi nad necim, co jinak vsichni povazuji za nehodne pozornosti. A prave tato miziva cast vedcu je motorem pokroku.
Zahady z definice vidi jen hloubavi jedinci a je jasne, ze zahady musime nejdrive rozpoznat, abysme je vubec mohli zacit resit.
Martin Plec,2012-06-26 09:32:40
Např. i Feynmann ve svých přednáškách z fyziky formuluje Heisenbergův princip neurčitosti tak, že "Nelze sestrojit přístroj, který by dokázal určit, kterou štěrbinou prošel elektron, bez toho, aby jej natolik neovlivnil, že by se neporušil interferenční vzorec." Je to sice v kontextu, kdy povídá o štěrbinovém experimentu s elektrony, na které se svítí světlem, ale závěrečná formulace je již tak obecná, jak jsem citoval. (Feynmannovy přednášky z fyziky, díl 5, str 19, slov. vydání 1990)
Ale zpět k těm Wikipedií citovaným pokusům. Ten novější experiment je sestaven tak, že se napřed zjišťuje vztah mezi štěrbinou kterou foton prošel a vlastnostmi druhého provázaného fotonu. Pak se odstraní měřidlo, které zjišťovalo štěrbinu, a sleduje se interferenční vzorec. A přitom se předpokládá, že vztah mezi štěrbinou, kterou prošel první foton, a vlastnostmi provázaného druhého fotonu se nezměnil.
Nějak se mi to nezdá - proč by se ten vztah neměl změnit?
tabulky
Maroš Štulajter,2012-06-25 14:26:24
vynikajúcim príkladom na prenos (meranie prepletených stavov je oscilácia neutrína. trochu ale nerozumiem grafu ktorý vysvetľuje zo štvorice na jeden prepletený stav 8 fotónov. tie tabuľky sú mi trochu nepresné. ak môžte tak by som vás poprosil o vysvetlenie.
ad p. Vaclav Knowledge-integration
Pavel Brož,2012-06-24 23:48:33
Doufám, že se Vás nedotknu svým odhadem, že jste filosof, ať už vzděláním, anebo filosof, který se nějakým omylem ocitl na studiu fyziky, případně ji i absolvoval. To nemyslím nijak pejorativně, prostě každý jsme nějaký.
Vzpomínám si, jak jednou jeden můj spolužák absolvoval dopředu prohranou diskuzi s jedním svědkem Jehovovým, který mu tvrdil, že bez Jehovovy vůle by ani auto nejelo. Onen spolužák se pokoušel protiargumentovat logickým sledem fyzikálních příčin – auto jede, protože ho pohání motor, který je poháněn rozpínáním spalin benzínu, které se rozpínají, protože došlo k výbuchu pohonné směsi ve válci, rozpínání se děje ve shodě s termodynamickými zákony, atd. atd.. Bylo úplně jedno, jak hluboko v tomto řetězci zašel, protože odpověď jeho protistrany byla vždy: „ano, ale toto se děje pouze proto, že tomu tak Jehova chce“.
K jakémukoliv fyzikálnímu, a obecně přírodovědnému problému lze vždy přistupovat s větší či menší mírou pragmatičnosti anebo naopak až jakéhosi teleologického „dobírání se smyslu“, či „nalézání vysvětlení“, která toho či onoho uspokojí či ne. Někomu stačí Maxwellovy rovnice coby plnohodnotný popis i vysvětlení elektromagnetických dějů, někdo jiný tvrdošíjně požaduje vysvětlení elektromagnetismu za použití Newtonových zákonů, a ještě někdo jiný považuje za mnohem podstatnější problém nalézt odpověď na otázku, kolik andělů se vejde na špičku jehly.
Uvádíte jakožto jeden z příkladů dodnes údajně nedostatečně vysvětlené věci imaginární jednotku i, jejíž kvadrát je minus jedna. Osobně jsem přesvědčen, že svého času znamenaly daleko větší převrat v matematice zavedení nuly, zavedení záporných čísel, či zavedení iracionálních čísel, jako je odmocnina ze dvou. Také ve všech těchto případech „staří profesoři“, kteří měli problém tyto věci přijmout, vymřeli, a nové generace „moderních vědců“ už s těmito fenomény neměly problémy. Také dnes, když se žáci učí o těchto věcech, tak většina z nich nakonec „skloní hlavu“, a „zařadí se do stáda“, místo aby vymýšlela vlastní neotřelé alternativy k těmto rigidním matematickým dogmatům.
Tím nechci říct, že člověk by měl být vždycky spokojený s tím, co vymysleli jiní lidé před ním. Dalo by se naopak říci, že naopak většina současných fyzikálních teorií vznikla právě poté, co jejich tvůrci byli nespokojení se stávajícím výkladem těch kterých jevů. Přesně takhle vznikla speciální i obecná teorie relativity, ale také nejprve „stará“ a následně „nová“ kvantová mechanika, a nakonec až standardní model. Nicméně pro prosazení těchto teorií nebylo nikdy rozhodující to, nakolik se komu zdály uspokojivě vysvětlené na úrovni jakéhosi „hlubšího, opravdového poznání světa“. Může se Vám to zdát nespravedlivé, ale fyzikální teorie byly vždycky ohodnocovány na základě shody s experimentem a jejich předpovědní síly.
Především Richard Feynman, kterého zmiňujete, neustále zdůrazňoval to, že bez ohledu na jakoukoliv krásu či estetičnost teorií to jediné, co opravdu rozhoduje o jejich oprávněnosti, je jejich praktická použitelnost – soulad s experimentem plus předpovědní síla. Mimochodem, ohledně diskuzí o interpretacích kvantové teorie, tak právě Feynman řekl, že se mu otevírá v kapse nůž pokaždé, když slyší o Schrödingerově kočce. Zrovna Richard Feynman by se nikdy nezařadil mezi lidi, pro které je dodnes nevysvětleným fenoménem imaginární jednotka, a pokud on je tím, který „sklonil hlavu“ a „zařadil se do stáda“, tak pak se hrdě a rád ocitnu v téže společnosti. Je určitě lepší být právě tam a ne ve společnosti originálních vynálezců třetění úhlu a kvadratury kruhu.
ops špatně zařazeno
Pavel Brož,2012-06-24 23:49:36
omlouvám se, mělo být pod komentářem v jiném vlákně
Odpovim take zde
Vaclav Knowledge-integration,2012-06-25 23:16:42
Historie fyziky vam samozrejme jde 'na ruku' pri poukazovani, jak tato veda sla kupredu s pouhym matematickym popisem reality bez starani se o jakakoli fyzicka vysvetleni. Tedy, ne ze by se nestarala, jen pri tom starani se skoro, ci prakticky vzdycky totalne selhala a tak se z toho selhani nakonec zpravidla udelala ctnost a jelo se dal.
Ja nerikam, ze kdyz se nedarilo prijit s nejakym fyzickym vysvetlenim toho ktereho fyzickeho jevu, ze se nemelo 'jet dal' (to by zbytecne zbrzdilo a treba i zastavilo dalsi vedecky pokrok), jen ze rezignace na to vysvetleni znamena politovanihodne selhani vedy. Ale pycha a arogance novych nastupujicich generaci vedcu nepripusti, ze se neco 'nevi' - vsechno prece vime a tak kdyz se nedari prijit s nejakym fyzickym, nebo nebo vseobecne nejakym hlubsim vysvetlenim, tak se to hodi na ramena reality, ze ona je proste takova, ze nepripousti hlubsi fyzicke poznani a byt dobrym vedcem znamena nahlednout tuto hlubokou pravdu. Taky je tu moznost odkazat se na nedokonalost vlastni, tedy nedokonalost cloveka, jehoz pojmy a zkusenosti jsou pouze z tohoto makroskopickeho sveta a jsou neprenosne do toho mikroskopickeho, a jsme z obliga.
Takovyto nahled je osvobozujici. Uz nemusime za bezesnych noci zpytovat zaklady jiz dosazeneho vedeckeho poznani, jestli jsme mozna nekde neucinili chybny krok a zbloudili jsme z cesty poznani, ale muzeme statecne razit cestu naslepo dal do neznama, v bezmezne vire, ze nam nejake slepe rameno rokliny, nebo casem dokonce cele nejake pohori nezastavi cestu vpred...
V nekterych pripadech je toto selhani nevinne, nema pro pokrok vedy zadne nasledky, jako napriklad v tom pripade imaginarnich cisel, porozumeni jejich podstaty. Tam se zrejme jedna jen o 'vedeni pro vedeni', cili neco jako zlezani hory, 'protoze tu je', jak horolezci tradicne zduvodnuji sve konani a rizika ktera podstupuji. Vubec nejde o to, co je dulezitejsi, co predstavuje vetsi prevrat (jestli zavedeni nuly, nebo zapornych cisel bylo vice prevratne). Vsemu se ma rozumet. Take ti lepsi vedci se chlubivaji badanim po pravde, po poznani, protoze je to proste pravda, ciste poznani, badani pro nejz nemusi byt jine ospravedlneni, nez jeho proste objasneni. Ale malokterym takovy ciry idealismus dlouho vydrzi, prakticky vsichni zahy skloni hrbety svych mysli nize a zameri se na snazsi cile, jini si vubec nejakych problemu ani nevsimnou...
V jinych pripadech, jako napriklad zahadna a nikdy neobjasnena konstantni rychlost svetla (a hlavne s tim souvisejici zalezitosti) pres pocatecni obrovsky pokrok v nasledujicim asi pulstoleti nakonec vedla do vyvojove slepe ulicky - ovsem 'veda si toho neni vedoma', ale dusledky ve forme stagnace zakladni vedy jsou zjevne. Z Obecne a Specialni teorii relativity je uz nejspis vyzdimano vse co se vyzdimat dalo, a zadna jina teorie ktera by je nahradila (popripade vylepsila) ani po stoleti uplynuleho casu neni v dohledu a napriklad ta zminena zahada setrvacnosti hmoty stale neni objasnena. Neni objasneny ani fyzicky princip ekvivalence gravitacni a setrvacne hmoty (jinak bysme ho opakovane nemerili na porad vice desetinnych mist).
A neni to tak, ze by vedci necitili potrebu pokroku, spis jen, ze ho nejsou schopni. A vsechno co bylo ve fyzice udelano v minulosti je temer definicne v poradku, uz se musi jen doladovat a jde se dal, systemovych zmen netreba. Ale to neni nic noveho, presne ta sama situace panuje v politice. Jenze nevyjasnene problemy se hromadi a neni na ne ani naznak odpovedi ani po dekadach, ci nejakeho temer pul stoleteho snazeni (temna energie, hmota), dalsim prikladem je ze porad nemame nejakou formu integrace jiz zavedenych teorii (QM & OTRelativity apod.).
------------
Souhlasim, ze v retezci pricin, v „nalézání vysvetlení“, se nemuzeme chtit dobrat nejakeho 'prvotniho impulsu'. To je iracionalni a veda to spravne odmita. Ale nema to slouzit k zakryvani „nalézání vysvetlení“, k pustym vymluvam, tam kde to racionalni a mozne je. A ja si myslim, ze vse je mozne vysvetlit, aspon do takove hloubky, kde rozumny clovek muze byt s vysvetlenim spokojeny. Nejde nakonec o prani nejakeho moc hlubokeho vysvetleni - uspechem by byla jakakoli hloubka vubec. Dneska se totiz casto vubec nedostavame pod povrch k jakekoli fyzice, ale kolikrat zustavame jen u matematickych rovnic. Ty priklady ktere jsem uvedl prece nejsou ani zdaleka na tak fundamentalni urovni, jako nejake dobirani se smyslu existence, prvotnich pricin, nebo neco takoveho (ty narazky vam promijim protoze me neznate a svet je jaky je). Jde prece o to, ze typicky mame ciste matematicky popis, u ktereho bud uplne chybi nejaka 'fyzicka kostra' na ktere by visel (nejaky fyzicky vyklad aspon nejake hloubky, treba i jen melky ale aspon nejaky a rozumne znejici, prijatelny), anebo tu nejaka je, ale nejsme s ni spokojeni a to oduvodnene (protoze vysvetleni ktera mame napriklad v kvantove mechanice jsou paradoxicka, zavani magii, a jinde, jako v pripade te konstantni rychlosti svetla (povysene na postulat teorie) a puvodu setrvacnosti hmoty a dalsi se spokojime s vysvetlenim zadnym, proste opomijime se tim vubec zabyvat.
---------------
Feynman sice zduraznoval tu prakticnost teorii, jak zminujete, ale taky ho hodne zajimal jejich vyklad, jako napriklad u te kvantove teorie, u ktere neopomel zduraznit, ze u jejiho zakladu je takovy a takovy paradox a kdyz jej prijmeme, vse co nasleduje je pak logicke. Ale odpoved (na tu zahadu dvojite skviry) nemel.
Krome toho, ja tu prece nezpochybnuji prakticke fungovani vselijakych tech matematickych teorii fyziky, ani v tech pripadech kdy jejich vyklad, pokud vubec nejaky maji, zavani esoterikou. Proste je ten vyklad spatny, teorie dobra (protoze experimentalne prokazana).
Jinak Feynman taky nebyl buh a plno veci nemusel vedet (mimo tech o kterych otevrene rikal ze jim fyzika nerozumi, coz byl velice prikladny pristup v mem hodnoceni), jako napriklad nerozumel mechanicke tocici se kace (spinning top), principu jeji precese popsane pouze pomoci vektoroveho momenta a niceho jineho, tedy tak aby se precese (vcetne nutace) dala pochopit naprosto intuitivne (i kdyz matematicky popis tohoto pozoruhodneho pohybu zvladal dobre jako kazdy jiny ucitel) a u imaginarnich cisel ho asi nenapadlo, ze je to neco, co by vyzadovalo vysvetleni - i kdyz prave u neho, jako u vyhlaseneho 'hracickare' bych ocekaval ze by se nad tim pozastavil. Ale nepozastavil. Nemuzeme ale od kazdeho chtit vsechno.
-------------------
Vsimnul jsem si jak vas tu pane Brozi lidi chvali, jak dovedete veci dobre vysvetlit. Ale abyste nakonec jen nevysvetloval, jak to a ono vysvetlit nelze, nebo ze zadne vysvetleni neni a neni ho ani potreba. To by byla dost ironicka hyperbola.
Chtel jsem se optat, kdyz napisu komentar ke starsimu clanku, zapadne to uplne, nebo si toho nekdo vsimne (myslim krome toho kdyz na ten clanek nekdo nahodne zabrousi)? Jako ze je tu nekde seznam poslednich pribylych komentaru?
prostě od malička víme,
Václav Malý,2012-06-25 23:33:17
že existuje něco, co umí působit na dálku bez nějakého mechanického kontaktu, napsal kdesi dole Pavel Brož Co umí působit na dálku? Je to snad nosič elektrického náboje, který „na dálku“ reaguje na jiné nosiče nábojů? Třeba elektron nacházející se v blízkosti nabité desky. Bude-li deska nabitá souhlasně, elektron se pohne směrem od desky. Bude-li nesouhlasně nabitá začne se pohybovat k desce. Jak zjistí kam se má pohybovat, když si na tu desku (resp. její náboj) nějak „nesáhne“? Já vím, kvanťáci vymysleli výměnu virtuálních fotonů mezi nábojem na desce a elektronem. Jenže ty jejich virtuálfotony jsou bez náboje; všechny stejný. Nemohou proto zprostředkovat odpuzování i přitahování! To nemá kauzální řešení. Řešení spočívá v tom, že oba náboje mají svá hmotová kvartonová pole svými náboji polarizovaná a těmito poli (které patří k nim) se „mechanicky“ dotýkají. Tedy žádné zázračné působení „na dálku“, ale docela těsné dotýkání se svými hmotovými poli.
Záhady
Marek Fucila,2012-06-27 03:22:14
Pán Vaclav Knowledge-integration. Vadia vám odpovede typu "nesprávne položená otázka". Poznatky, ku ktorým sa v rámci danej teórie pristupuje ako k faktom, pretože niečo vysvetlili a ich odôvodnenie je len to, že bez nich by sme realitu takto nepozorovali, považujete za záhadu. Zároveň súhlasíte s nezmyselnosťou hľadania prvotného impulzu v reťazci príčin. Pýtam sa teda, čo by ste považovali za uspokojivú odpoveď.
Zaujímal by ma príklad gravitačnej teórie, s ktorou by ste nemali problém. Nemusí ísť (ani nepôjde) o teóriu odrážajúcu svet, ale skúste formulovať čo by taká nepotvrdená teória hovorila, s čím by ste vy nemali problém.
Tiež by ma zaujímal Váš postoj k imaginárnym číslam. Sú neintuitívne, teda neexistujú? Nemáme ich používať? Alebo chcete skôr povedať, že máme hľadať riešenia kvadratických rovníc v len reálnych číslach? Alebo máme namiesto imaginárnych čísel rozšíriť reálne čísla o nejaký zatiaľ nedefinovaný typ prvkov, ktoré nebudú ako imaginárne, ale buú pre nás pochopiteľnejšie?
re: Záhady -Marek Fucila
Vaclav Knowledge-integration,2012-06-27 12:02:28
"Pýtam sa teda, co by ste považovali za uspokojivú odpoved."
Uspokojiva odpoved by byla odpoved, ktera by ten ktery dany fenomen integrovala v oblasti, do ktere prinalezi. Cili ze napriklad imaginarni cisla by logicky vyplyvala z cisel (cisel jako takovych), ze kterych obratem vyplyvaji cisla kladna a zaporna napriklad (puvodne jsme meli jen cisla, jejich deleni na zaporna a kladna prislo az pozdeji). A setrvacnost hmoty by logicky vyplyvala z gravitace, protoze 'princip ekvivalence' nam napovida, ze mezi temito fenomeny existuje navysost intimni vztah (ze to musim napsat takhle).
Integrovat znamena 'zaradit', nebo 'spojit' dohromady, a to za ucelem abychom vecem porozumeli. Bez integrace, tedy kdyz mame jen nespojite kousky znalosti, doopravdy vecem nerozumime. Vedeni sestava z porozumeni dane veci v ramci ostatnich vedomosti v te ktere oblasti vedeni. Clovek nepotrebuje znat vsechny vedomosti do nejake bozske hloubky, ale jen do takove, aby se tyto zaradily mezi ostatni jeho vedomosti, aby jedny vedomosti vysvetlovaly druhe, jde o vzajemne vysvetleni danych vedomosti v ramci vsech ostatnich (vsechny vedomosti jsou pak hloubeji ukotvene v tzv. axiomech poznani kterych je jen nekolik a jsou logicky zduvodnene).
Z toho tedy vyplyva, ze vecem bychom meli rozumet do prave a jen do takove hloubky, aby bylo dosazeno zarazeni toho ktereho fenomenu do sirsi, tomu fenomenu prinalezici oblasti poznani.
Takze zadne kosmicke pravdy nas nemusi zajimat. Jedine co nas musi zajimat je aspon takova hloubka poznani, aby nase vsechny nase vedomosti byly spojite, tedy aby vytvarely jeden jediny velky logicky, spojity celek. To je stav ke kteremu bychom idealne meli smerovat.
---------------
"Váš postoj k imaginárnym císlam. Sú neintuitívne, teda neexistujú? Nemáme ich používat?"
Muj postoj je presne opacny. Imaginarni cisla evidentne funguji a proto by nas melo zajimat, proc funguji. Meli bychom to fungovani vysvetlit.
Vyse pan Ondrej Adamovský uvedl, ze "nejaký matematik si rekl, co by se asi stalo, kdybych mel císlo, jehož druhá mocnina je -1". My ovsem vime, ze historicky nebylo k imaginarnim cislum dospeno takhle frivolne, moderne, cestou co by bylo kdyby..., ale vyplynuly jako nutnost pri reseni jistych rovnic, ktere rovnez nebyly jen tak vytazene z rukavu, ve stylu 'co kdyby'. Cili imaginarni cisla jsou 'legitimni', nezpochybnitelny nastroj matematiky a na nas je jen nalezt pro ne patricne oduvodneni a to v ramci ostatnich podobnych nastroju matematiky, tedy v ramci ostatnich cisel jiz zavedenych a porozumenych.
Objeveni imaginarnich cisel se podoba pozdejsimu objevu kvanta - to take nebylo intuitivni, a Max Planck byl k jeho postulovani doslova tahnuty za vlasy, proti sve vuli. Ale bylo to jedine logicke, mozne reseni problemu 'ultrafialove katastrofy' zareni cerneho telesa. A jak kvantum, tak imaginarni cisla jsou dodnes nevysvetlena a obdobou otazky 'proc kvantum' v kvantove mechanice je 'proc imaginarni cisla' v matematice.
Dnes sice imaginarni cisla nepozivaji takovy status zahady jako kvanta, ale fakticky maji za sebou mnohem delsi historii kontroverse jejich prijeti, neprijeti, statusu v matematice.
Mala uprava
Vaclav Knowledge-integration,2012-06-27 12:07:12
Napsal jsem "Cili ze napriklad imaginarni cisla by logicky vyplyvala z cisel (cisel jako takovych), ze kterych obratem vyplyvaji cisla kladna a zaporna napriklad "
Ale radsi bych to napsal takhle:
'Cili ze napriklad imaginarni cisla by logicky vyplyvala z kladnych a zapornych cisel, ktera zase obratem vyplyvaji z cisel jako takovych (protoze puvodne jsme meli jen cisla)'
matematika
Marek Fucila,2012-06-27 13:28:05
Aha, takze problem bude v tom, ze Vy ani tak nemate problem s fyzikou, ako s matematikou samotnou:
"Cili ze napriklad imaginarni cisla by logicky vyplyvala z cisel (cisel jako takovych),"
Odporucam Vam precitat si Hofstadterovu knihu "Gödel, Escher, Bach: An Eternal Golden Braid", kde vysvetluje Gödelovu snahu o dokazanie uplnosti matematiky, pricom dospel presne k opaku. Mozno nepouzivam spravne pojmy, matematik nie som, ale ta kniha je pisana pre laikov a ako tomu ja rozumiem, Vasa snaha je marna. Imaginarne cisla nikdy nebudu vychadzat z realnych cisiel ci sa vam to apci alebo nie, pretoze tie realne maju prakticke nedostatky, kvoli ktorym je treba mnozinu rozsirit. A hoci nepoznam nadmnozinu komplexnych cisiel, viem si predstavit, ze na urcitu triedu problemov by sa dala rozsirit aj ta. Ono totiz ten Gödel dokazal to, ze ani mnozina prirodzenych cisiel "neospravedlni" samu seba. Ak som v obraze, inak povedane ze na rozhodnutie o pravdivosti tvrdeni v prirodzenych cislach musime externe dodefinovat nadmnozinu, v ktorej uy dane tvrdenia budu dokayatelne/vzvratitelne, a na rozhodnutie o pravdivosti vsetkych tvrdeni v nej ju treba rozsirit este viac, a tak sa da pokracovat az do nekonecna.
Mozno lahsie pochopitelny priklad z tej knihy bola snaha odvodit axiomu o sucte vnutornych uhlov trojuholnika v euklidovskej geometrii. Z ostatnych axiom sa tato odvodit nedala. Nakoniec sa ukazalo, ze plati len v rovine. Odvtedy mame tych geometrii viac. A studenti dnes mozu rovnako dobre neverit imaginarnym cislam ako neeuklidovskym geometriam bez ohladu na to, ako dobre popisuju pozorovany svet.
cisla
Marek Fucila,2012-06-27 13:31:35
Co presne chcete povedat tvrdenim "...z kladnych a zapornych cisel, ktera zase obratem vyplyvaji z cisel jako takovych..."? Nemam dojem, ze by sem mali cisla ako take a uz vobec nie, ze by z nich nejake kladne alebo zaporne cisla vyplyvali. Ani realne cisla nevyplyvaju z prirodzenych. Su dodefinovane, lebo prirodzene cisla nam na vela problemov nestacia.
Kladna a zaporna cisla
Vaclav Knowledge-integration,2012-06-27 19:48:19
Puvodne jsme meli jen prirozena cisla 1, 2, 3, atd na pocitani veci, pozdeji se zavedly operace scitani a odecitani a pak nekoho napadlo odecist vetsi cislo od mensiho a nasledkem toho bylo zapotrebi rozdelit dosavadni prirozena cisla na dve skupiny, oznacena znamenky. Ze zacatku lide meli mozna jen zaporna cisla a cisla prirozena. Kladna cisla byla nejspis zavedena az o neco pozdeji. Kladna a zaporna cisla nejsou nic jineho, nez prirozena cisla rozdelena specialnim oznacenim do dvou skupin cisel.
Proto nemichame prirozena a kladna/zaporna cisla. Na spocitani ovci nam staci ta prvni, prirozena cisla, ve skole na zakladnich stupnich potrebujeme ta druha. Ale to nejsou nejaka jina cisla, ale jak jsem rekl, proste jsou to znacenim +/- rozdelena prirozena cisla do dvou ciselnych skupin. Jedna se o vice abstraktni pouzivani prirozenych cisel.
Ovsem dnes v cislech vladne dost zmatek. Napriklad Wikipedia rika, ze "Prirozeným císlem (císlem z oboru prirozených císel) se v matematice rozumí kladné celé císlo (1, 2, 3, …)."
Ale ja rikam, ze prirozena cisla nejsou kladna, jsou to jen cisla, jaka pouziva baca na to pocitani ovci. Cisla jsou kladna az v kontextu, v souvislosti kdyz zacneme pouzivat take zaporna cisla. Bohuzel kladna cisla nemusi byt (z principu veci) vzdy oznacena kladnym znamenkem (protoze pocitani funguje dobre i bez takoveho znaceni), ale to nas nesmi mylit, anebo nemelo by.
-------------
A prave tak jako kladna a zaporna cisla jsou jen 'prevlecena' prirozena cisla, tak imaginarni cisla by mohla byt napriklad 'prevlecena' zaporna a kladna cisla...
kladná, záporná a komplexní čísla
Ondřej Adamovský,2012-06-27 23:57:44
záporná čísla se začala objevovat především s rozvojem obchodování. Bylo třeba nějak rozlišit má dáti a dal. Pochybuji, že by kdy kdo hleděl na dluh jako na převlečené bohatství (zde prosím nechytat básnicky za slovo).
Nechápu ten váš pojem "rozdělení" původních přirozených čísel na kladná a záporná. Ať se na to dívám jak chci, něco muselo být přidáno. Buď byla k původně kladným číslům přidána záporná, nebo byla původně přirozená čísla rozšířena o jeden atribut s dvěma možnými hodnotami. Každopádně přibyla nová kvalita, která nijak nevyplývala z vlastností přirozených čísel, nýbrž z jejich kombinace s potřebou nějak vyjádřit rozdíl menšího a většího přirozeného čísla.
Podobně komplexní čísla vznikla tak, že matematici zkoumali problémy, jejichž řešení vyžadovala druhou odmocninu, a potřebovali se nějak vypořádat se situacemi, kdy jim pod odmocninou vycházelo záporné číslo. (když výše tvrdíte, že říkám, že si příslušný matematik jen tak z plezíru žekl, co kdybych zkusil počítat s odmocninou z -1, tak nemáte pravdu. Svou větu jsem uvodil poznámkou o časté potřebě matematiků pracovat s množinami čísel uzavřenými nad určitou operací, zde jsem implicitně předkoládal potřebu uzavření na druhou odmocninu. Zda se mi to podařilo vyjádřit dostatečně dobře nechť posoudí ctěný čtenář)
Matematici nejprve zkoušeli prostě počítat s tou odmocninou záporného čísla jako s dalším číslem, ale docházeli k rozporuplným výsledkům. Po několika desetiletích tápání pak jednoho matematika napadlo tyto odmocniny záporných čísel separovat, odlišit od reálných čísel, a vznikla imaginární jednotka a aritmetika komplexních čísel, což umožnilo vypočítat odmocninu z jakéhokoliv reálného čísla. Za pár staletí to pak další matematici elegantně zobecnili na obecnou mocninu, takže komplexní čísla jsou uzavřená nad oprecí umocnění komplexního čísla komplexním číslem. Ve svém původním příspěvku jsem to napsal zjednodušeně, jakoby šlo o pouhé odpolední cvičení jednoho matematika, protože se mi nechtělo psát romány, na podstatě věci to ale nic nemění.
Komplexní čísla přímo vyplývají ze snahy uzavřít množinu Reálných čísel na operaci umocnění (nebo její zvláštní případ druhou odmocninu). Stejným způsobem, jako celá čísla vyplývají ze snahy uzavřít množinu přirozených čísel na odečítání. Ať se snažím, jak se snažím, nemohu v tom najít žádný podstatný rozdíl.
Historie cisel a jeji ucel
Vaclav Knowledge-integration,2012-06-28 13:43:07
"Bud byla k puvodne kladným císlum pridána záporná, nebo byla puvodne prirozená císla rozšírena o jeden atribut s dvema možnými hodnotami. Každopádne pribyla nová kvalita, která nijak nevyplývala z vlastností prirozených císel"
Tak 'nova kvalita' samozrejme nevyplynula nejak logicky z vlastnosti prirozenych cisel, ale byla tak rikajic 'naroubovana' na tato cisla. Chtel jsem jen rici, ze kladna a zaporna cisla nejsou nejaka nova cisla, ale ze jsou to ta stara prirozena cisla - jen oznackovana znamenky plus a minus. A ze logicky nejdriv musela byt zavedena zaporna cisla, kladna az nejaky cas pote, jako nasledek, aby se tato nejak vymezila oproti zapornym cislum (aby byl system cisel konzistentni, uniformni, nebo jak to jinak vyjadrit, proste aby vsechna cisla byla 'oznackovana', ne jen jejich cast).
Jak jsem napsal vyse, znamenko + se pred kladna cisla nepise, ale jen protoze se samo rozumi. Kdybysme meli, nebo chteli byt striktni, museli bysme je psat vsude (protoze krome let predchazejicich skole a vcetne prvni tridy se prirozena cisla ve skolach nepouzivaji). Ale nepiseme je protoze to pro porozumeni neni treba (a taky by to bylo neprehledne a pracne - treba bysme museli psat +1 + +1 = +2 a pak bysme museli davat kazde +1 anebo scitaci znamenko do zavorky aby to bylo prehledne...). Ale to ze znamenko + pred kladna cisla automaticky nepiseme by nas nemelo plest a nemeli bysme tedy rikat, ze prirozena cisla jsou kladna cisla. Atribut 'kladny' prirozenym cislum vubec neprinalezi. Jsou to jen 'hola' cisla, jako ta ktera pouziva baca pri paseni ovci, aby vedel kolik jich ma.
Dale pak rikam, ze imaginarni cisla jsou take jen slozena z cisel, v posledku z tech prirozenych. Ale vice primo vyrustaji z kladnych a zapornych cisel, asi tak jako tato cisla obratem vyrostla z cisel prirozenych. Zadnou velkou vedu v tom nehledejte, ani nemusite pouzivat odborne vyrazy (takze 'prevlecene' a podobne vyrazivo je zadouci). Odborne vyrazy zpravidla slouzi jen jako maska, za kterou se odbornici schovavaji jako za teflonovy stit autority.
Kladna cisla bez zapornych je nesmysl. Proti cemu by se asi vymezovala? Jak rikam, zeptejte se baci jestli ma kladny pocet ovci na louce a jestli je pocita kladnymi cisly a mozna dostanete bejkovcem po zadech, ze si z nej utahujete.
Rici, ze prirozena cisla jsou kladna je svedectvim mozku, ktery neumi pouzivat pojmy, ale pouze je papouskuje. A neni divu, ze s takovym pristupem k veci potom nemuze prijit na koren imaginarnim cislum, ale bude tato brat jako dar od boha.
Historicky jde o to, ze nejake zavadeni abstraktnich vymozenosti do matematicky se vubec nenosilo, vzdycky jejich prijeti vyzadovalo hodne dlouhy cas (napriklad zavedeni nuly - proc mit 'nejakou' znacku pro 'nic') . A imaginarni cisla pres nejake to casne koketovani s nimi na bazi 'co by bylo kdyby' musela pockat az na ty rovnice, ktere se daly resit jen za pouziti odmocniny zaporneho cisla (tam kladou historici puvod jejich zavedeni). Pozdeji myslim Gauss zavedl imaginarni jednotku 'i' jako standardni znaceni a vahou sve autority a snad i aplikacemi techto novych jednotek se zaslouzil o sirsi prijeti techto novych 'cisel' do matematiky.
Ale o presnou historii nema cenu se nejak moc prit. U cisel nakonec jde o vnitrni logiku veci a jejich vznik a vyvoj se da do znacne miry zrekonstruovat vice mene logickym uvazovanim. Napriklad je nesmysl, aby pred zavedenim zapornych cisel (oznacenim prirozenych cisel znamenkem minus a nazyvanim je zaporna cisla) nekdo pohlizel na prirozena cisla jako na kladna - i kdyz videno zpetne je mozne jim mylnym uvazovanim tento atribut prifarit.
Ale jak rikam, na tom nic praktickeho nestoji ani s tim nepada, na vyvoj matematiky takovy nahled na prirozena cisla uz drahnou dobu nema zadny vliv. Ale dokud byla matematika jeste v plenkach, tak to vliv melo. Dneska to ma vliv uz jen na 'cistotu mysli', tedy jak to kdo ma v hlave usporadane a jak bude treba zpusobily objasnit puvod imaginarnich cisel v cislech jiz dobre zavedenych.
-------
Jinak vam dekuji za diskuzi, neberte me urcite nahledy na matematiky nejak osobne, aspon to neni tak mysleno.
Ondřej Adamovský,2012-06-29 13:22:40
omlouvám se, jestli jsem byl příliš agresívní. Zdálo se mi, že mne chytáte za slovo. Snad šlo pouze o vzájemné neporozumnění.
Rovněž děkuji za vyprovokování k zaregistrování a ke vstupu do dikuse.
Marek Fucila,2012-06-30 03:02:59
Pán Vaclav Knowledge-integration, opakovane to tu bolo spomenuté, a váš problém nie je ani tak v chápaní imaginárnych čísiel ako v pochopení súvislosti teórie čísiel a teórie množín. Akokoľvek sa na to budete snažiť pozerať sedliackym rozumom, nezmeníte fakt, že žiadna množina čísiel nevyplýva z tej druhej. Nadmnožina je vždy dodefinovaná. (Podmnožinu tiež niekto musí určiť.) Keď mám prirodzenú jednotku a odpočítam 2 bez existencie záporných čísiel dostanem neplatný výsledok. Vôbec to neznamená, že "musí" existovať nejaké záporné čiňíslo. Ja "chcem" aby bolo, tak také vytvorím. Záporné čísla by nemuseli byť, keby sme ich nepotrebovali.
Problém je v tom, že vy nevidíte rozdiel medzi definíciou a pozorovaním. Pri pozorovaní má zmysel snažiť sa pochopiť, čo vidím. Pri definícii sa môžem maximálne tak snažiť pochopiť motiváciu toho, čo ju vytvoril. A samozrejme máte voľné pole vytvárať alternatívne definície. Či už ma označíte za hlupáka šedej masy alebo len za nedostatočne hĺbavého, nevidím žiaden dôvod zamýšľať sa nad definíciou komplexných čísiel. A naopak čím rýchlejšie ju príjmem, tým skôr som schopný počítať príklady. Z vlastnej skúsenosti musím priznať, že hlbšie pochopenie komplexných čísiel u mňa nastalo až po pár semestroch. Myslím, že skúsenosťami človek získava nadhľad, ktorý mu s odstupom času dá odpovede na otázky, ktoré vy hľadáte.
Skrátka žiadne čísla, akokoľvek prirodzené sa Vám zdajú, v prírode de-facto neexistujú. Je to myšlienkový model v hlave pozorovateľa, a žiaľ ak má byť užitočný, je potrebné niektoré nosné prvky určiť lusknutím prsta s pokrikom "a takto to bude". Matematikárka na základnej škole nám zvykla definície uvádzať vetou "matematici sa dohodli, že...". Matematika by skrátka mohla byť aj inak postavená. Ale čo by určite inak nemohlo byť je to, že by sme mali na začiatku zopár axióm, z ktorých by vyplynulo absolútne všetko, aj vami zaznávané komplexné čísla. Tu matematickú fantáziu žiaľ brzdí logika, a ako som už písal, pred storočím napadlo jednému matematikovi pozrieť sa na to inak, a keď budete pátrať po "filozofickom odkaze" jeho dôkazov, zistíte, že zabíjate čas dopredu prehraným bojom. Myslím, že matematika má aj ďaleko abstraktnejšie štruktúry ako sú čísla. A ani ten bačo by nič nevedel o prirodzených alebo neprirodzených číslach, keby nemusel chodiť do tej ľudovej, kde by mu objasnili ako je to dohodnuté.
Určení cesty částice bez rozbití interferenčního v
Martin Plec,2012-06-22 15:13:16
Ve Wikipedii (http://en.wikipedia.org/wiki/Double-slit_experiment) se píše:
But an [double-slit] experiment performed in 1987 produced results that demonstrated that information could be obtained regarding which path a particle had taken, without destroying the interference altogether. This showed the effect of measurements that disturbed the particles in transit to a lesser degree and thereby influenced the interference pattern only to a comparable extent. And in 2012, researchers finally succeeded in correctly identifying the path each particle had taken without any adverse effects at all on the interference pattern generated by the particles.
Jestli je to pravda, tak to dost popírá, co jsme se učili ve školách - že vědomost o tom, kterou štěrbinou částice prošla zruší interferenční vzor.
Víte někdo o těchto experimentech něco bližšího, zejména jak moc jsou věrohodné?
Mj B,2012-06-25 08:43:19
Vědomost o cestě interferenci vedoucí vlny nezruší. Zruší jí pouze přímé měření (kolize např. s fotonem) Zde se přímému měření šikovně vyhnuli tím, že měřili entaglovanou částici a podle výsledku usoudili cestu púvodní částice.
Někde jsem zde posílal okdaz na přijatelnou interpretaci QM (tzn. bez metafyzkických pojmů jako vědomí pozorovatele, atp.)
Martin Plec,2012-06-25 09:50:35
To, co píšete, není pravda. Budu citovat např. z vámi odkazovaného článku:
"If, by any means whatsoever, it is possible to determine the slit through which the particle passes, the interference pattern will be destroyed."
Přesně totéž jsem četl nebo slyšel nespočetněkrát: Pokud je někde ve Vesmíru informace o tom, kterou dírou částice proletěla, tak interference zmizí. (Vždy mě překvapovalo, jak si to někdo vůbec troufne takhle obecně formulovat.)
A nebo z komentáře k těm experimentům odkazovaným ve Wikipedii (http://arstechnica.com/science/2012/05/disentangling-the-wave-particle-duality-in-the-double-slit-experiment/):
"The reason that this experiment is significant is that to-date, any experiment that attempted to extract which-path (or which-slit) information from the photons or electrons traveling through the slit would destroy the interference pattern.
If the detectors are turned off, the interference pattern reappears. When the detectors are turned on, the photon is determined to go through exactly one of the slits/paths, and the interference pattern disappears."
Kromě toho, každému vědění (kudy elektron proletěl) předchází měření (byť nepřímé).
Mj B,2012-06-25 10:44:41
V tom samé odstavci, ze kterého citujete je dále psáno, že je třeba vzít v potaz způsob měření. Mluví se tu o interakci s měřícím systémem.
Já nejsem fyzik, jen pouhý programátor. A pokud si přectu že když detektor zapnutý, chová se to takto a když vypnutý, chová se to jinak, tak mě to tak trochu naštve, protože je přece nutné dodat co ten detektor vlastně v zapnutém stavu dělá : jestli např. na elektrony 'svítí', nebo je např. ovlivňuje magnetickým polem...
Pavel Bílek,2012-07-04 23:21:10
Myslím si, že pokus popsaný na http://arstechnica.com/science/2012/05/disentangling-the-wave-particle-duality-in-the-double-slit-experiment/ je interpretován špatně. Když docházelo k interferenci, byl stav signálního fotonu "prošel oběma štěrbinami". To je superpozice stavů "prošel levou štěrbinou" a "prošel pravou štěrbinou", leč který stav je bázový a který stav je superpozicí jiných stavů, to je věc popisu. Záleží na nás, kterou bázi si při popisu zvolíme. Báze, ve které měřili idler foton, dávala výsledky, které nelze interpretovat jako informaci o štěrbině, kterou prošel signální foton mající stav "prošel oběma štěrbinami".
kolaps
Maroš Štulajter,2012-06-21 17:01:44
vysvetlite mi prečo je kolaps vlnovej funkcie pri meraní. napr. oscilácie neutrín môžme zmerať v danej chvíli kvadrát hmotnosti, ale ďalej pokračuje daná vlnová funkcia danej rovnice.
Kolaps vlnovou funkci změní
Vladimír Wagner,2012-06-21 17:46:20
Jestliže změříme polohu elektronu, tak se vlnová funkce změní. Rozložení vývoje pravděpodobnosti polohy elektronu v čase je úplně jiné, než bylo před měřením. Stejně tak, pokud provedeme měření u neutrina. Pokud máme při oscilacích stav, který je směsí tří různých neutrinových stavů, tak změřením, při kterém určíme typ neutrina, se vlnová funkce popisující stav dramaticky změní. Takže po měření už nemáme původní vlnovou funkci a ta nepokračuje.
Argumenty proti intuitivním interpretacím
Martin Plec,2012-06-21 11:44:35
Shlédl jsem video odkazované v článku (http://www.youtube.com/watch?v=s3ZPWW5NOrw). Zeilinger zmiňuje dva argumenty, proč ty pokusy o intuitivní interpretaci QM, které jsou zmiňovány v předchozích příspěvcích, nejsou správně.
Jednak jsou to interferenční vzory, které by nevznikaly, kdyby výsledky byly dopředu určené.
A za druhé to ukazuje na příkladu s kalíšky (ve videu od 29:30). Lze totiž realizovat pokus(y), který by v případě, že by byl jeho výsledek určen již v minulosti, dával jiné výsledky (pravděpodobnostní poměry), než které se ve skutečnosti měří.
Přesně tak
Vladimír Wagner,2012-06-21 13:44:44
Přesný popis jednoho z takových experimentů, který je standardním potvrzením nelokálnosti kvantové fyziky je popsán i s rozdílem mezi příslušnými pravděpodobnostmi, které výjdou v případě lokálnosti teorie (to jaká barva je pod kalíšky je dáno už při vzniku systému) nebo nelokálnosti (barva není určena před měřením, tedy kouknutím se, co je pod kalíšky). Takže opravdu lze nelokálnost potvrdit a je nezvratně prokázáno, že dané velčiny kvantového stavu nejsou před měřením (příslušnou interakcí) určeny. Blíže v tom článku o podivnostech kvantového světa: http://www.osel.cz/index.php?clanek=5110 .
No,
Tomáš Bartoň,2012-06-21 16:32:03
na to aby někdo o čemkoli v kvantovce mohl prohlásit "je nezvratně dokázáno" si imho budeme muset opravdu ještě nějaký pátek počkat :-)))
Právě naopak
Vladimír Wagner,2012-06-21 17:52:35
Kvantová fyzika je už docela dlouho standardní teorie, u které je řada faktů a jejich aspektů nezvratně prokázána. Jinak by nefungovala řada našich přístrojů a nebyli bychom schopni vyrábět řadu zařízení, která využíváme. Pochopitelně je u ní stále velké množství stále otevřených záležitostí a některé filosofické otázky s ní spojené mohou zůstat otevřeny možná i navěky, ale to neznamená, že by řada jiných faktů a zákonitostí nebyla spolehlivě prokázána.
Další odkazy
Martin Plec,2012-06-22 14:29:44
Ještě bych rád upozornil na diskuzi pod jiným zde odkazovaným článkem, http://www.osel.cz/index.php?clanek=5110&akce=show2&dev=1#diskuze. Pavel Brož tam moc hezky osvětluje různé interpretace QM. Ne že bych se všemi jeho výhradami k těm různým interpretacím souhlasil, ale i tak to určitě stojí za přečtení.
Zároveň je z toho vidět, že co jednomu fyzikovi přijde jako akceptovatelné a přirozené vysvětlení, to jinému připadá přitažené za vlasy. Holt kolik hlav, tolik vidění světa.
Zároveň si však myslím - asi na rozdíl od Pavla Brože - že snaha o nalezení přijatelné filozofické interpretace QM není pouhá kratochvíle, přesto že se za to Nobelovka neuděluje. Protože pomáhá vytvořit model, ve kterém veškeré podivnosti QM budou vypadat přirozeně, intuitivně a nebudou vzbuzovat nedůvěru, pochybnosti a odpor. A i my amatéři, kteří matematiku za QM neznáme, si pak můžeme myslet, že jsme do principů QM aspoň částečně pronikli.
ad p. Martin Plec
Pavel Brož,2012-06-22 22:41:33
Dobrý den, jenom že jste zmínil můj tehdejší komentář, tak bych ho možná ještě trochu doplnil. Někdy si tak říkám, že opravdový přelom v chápání kvantové mechaniky přijde až tehdy, až někdo vymyslí „kvantově mechanickou hračku“, na které odroste úplně nová generace lidí, tedy i fyziků, pro které pak budou pro nás stále tak překvapivé zákonitosti kvantové mechaniky věcmi dobře známými už z dětství. Vezměte si třeba elektrické a magnetické jevy - s těmito věcmi se člověk setkává běžně už od svého dětství, a osobně si myslím, že právě to je jeden z důvodů, proč se vůbec nepozastavujeme nad tím, že lze magnetem zvednout železný předmět, ani nám nepřijde nijak moc divné, že magnetické pole Země nás umí chránit před nabitými částicemi, a stejně tak nepřekvapí, že po stisknutí vypínače se prakticky okamžitě rozsvítí světlo i ve velmi velké vzdálenosti.
Možná že právě takováto kvantově mechanická hračka povede k tomu, že na ní odrostlá generace fyziků se už nebude upínat k vysvětlování kvantových jevů na základě analogií z nekvantového světa. My dnes také necítíme nutkání vysvětlovat třeba magnetické pole pomocí Newtonovské mechaniky – prostě od malička víme, že existuje něco, co umí působit na dálku bez nějakého mechanického kontaktu, a nepřijde nám to zvláštní. Vždycky tomu tak ale nebylo, tak např. v devatenáctém století fyzici popsali stohy knih v marné snaze ukotvit elektromagnetismus na nějaký v té době akceptovatelný mechanistický základ – spousta z těch knih se věnovala vlastnostem éteru coby mechanického prostředí, jehož kmitání a deformace by vysvětlovalo většinu, ne-li všechny elektromagnetické jevy. A koneckonců prvotní Faradayovo intuitivní pojetí elektromagnetického pole pracovalo s představou spousty neviditelných pružinek působících mezi elektricky nabitými tělesy.
Dnes už tyto mechanistické modely elektromagnetismu považujeme právem za překonané (dodnes ale představují velice poučné milníky, kudy se ubíralo poznání těchto jevů). Stejně tak se může stát, že za nějakých padesát či více let bude pro příští fyziky nepochopitelné, že jsme se tak dlouho a urputně pokoušeli namalovat obraz kvantově mechanických dějů za použití nekvantového štětce a plátna.
Samozřejmě, že osvojení si daného okruhu jevů jakožto něčeho běžného, nejlépe už v dětském věku, není nezbytnou podmínkou pro úspěšný popis a využívání těchto jevů. Tak např. James Clerk Maxwell přetavil Faradayovu mechanistickou představu do abstraktního popisu s využitím vektorové analýzy, ve které jsou elektromagnetické děje popisovány pomocí vektorových funkcí měnících se od bodu k bodu – kterým dnes obecně říkáme vektorová pole, speciálně pak v případě elektromagnetismu tyto vektorové funkce nazýváme intenzity elektrického a magnetického pole. Díky Maxwellovi pak následující generace matematicky erudovaných fyziků a inženýrů dokázala velice dobře popisovat a předpovídat spousty nových elektromagnetických projevů. Nicméně přerod paradigmatu, o kterém se zmiňuji výše, vůbec nevyžaduje znalost matematiky – drtivá většina lidí, ač bez znalosti vektorové analýzy, nemá dnes problémy s akceptováním elektromagnetických dějů, a to nikoliv proto, že se o nich učili na vysoké škole, ale proto, že se s nimi naprosto běžně setkávali už od dětství.
Dnes jsme u chápání kvantové mechaniky stále ještě v situaci, jaká u chápání elektromagnetismu panovala po Maxwellovi – máme velice solidní matematický popis kvantové mechaniky, nicméně intuitivně stále ještě tápeme a zoufale se snažíme vytvořit si nějaký „přijatelný“ nekvantový model kvantově mechanických dějů. Možná jedinou věc, kterou potřebujeme, je právě nějaká kvantově mechanická hračka, se kterou se budou moct běžně setkávat už malé děti. Může to být hračka postavená zrovna na nám tak nepochopitelném entanglementu, kdy pozorování dvou prostorově odlehlých částí systému vykazuje právě ony nepochopitelné korelace.
Jak by taková hračka mohla vypadat? Asi určitě by nebyla postavená na entanglovaných párech fotonů, určitě by totiž nebylo realistické očekávat, že součástí hračky budou všechny ty nezbytné laboratorní přístroje, které umožňují ten entanglement vůbec prokázat. Muselo by to být něco makroskopického – možná třeba něco založeného na Bose-Einsteinových kondenzátech, kde se entanglement může projevovat dokonce na souborech triliónů či více částic. Samozřejmě, v dnešní době jsou pro vytvoření těchto kondenzátů stále ještě nezbytné extrémně nízké teploty, které není možné docílit bez mnoha složitých přístrojů kolem (např. supratekuté hélium je asi nejstarším známým příkladem Bose-Einsteinova kondenzátu). Nicméně třeba v tomto směru dojde v příštích desetiletích k pokroku, a bude pak možno pozorovat Bose-Einsteinovy kondenzáty v „hračkách“ velikosti třeba nanoakvária pro malé krevetky či autíčka na dálkové ovládání, a to vše při pokojové okolní teplotě.
Tím samozřejmě neříkám, že nemůže dojít k průlomu přímo na poli sofistikovaného matematického chápání kvantové teorie, mám tím na mysli na poli interpretací kvantové teorie. Možná že už zítra někdo přijde s tak převratnou novou interpretací, že se většina fyziků plácne do čela a řeknou si – „No jo, jak to, že jsme to dříve neviděli“. Ale možná ten hlavní přerod nebude mít s matematikou ani filosofií nic společného – koneckonců, matematický popis kvantových jevů je už desítky let naprosto vyhovující a plně postačující pro vytváření všech potřebných teoretických předpovědí. To, co nám stále schází, je ale dost možná právě ta samozřejmost těch jevů, a právě tento nedostatek nás znovu a znovu tlačí do hledání stále nových kvadratur čtverce.
P. Broz - prelom v chápání kvantové mechaniky
Vaclav Knowledge-integration,2012-06-24 12:38:21
Nemyslim ze to funguje jak to tu popisujete. To co tu popisujete neni nic jineho, nez 'prani je otcem myslenky' a take rezignace na hlubsi, opravdove poznani sveta. Opravdu premyslivym jedincum je i dnes elektromagnetismus zahadny, je jim zahadna i gravitace a imaginarni cislo 'i' a dalsi jevy cekajici na vysvetleni, vcetne tech quantum mechanickych.
Kdyz Newton prisel se svou teorii gravitace, taky byl napadan, ze vlastne vubec nevysvetlil jeji fungovani a dokonce byl z toho titulu narcen z tmarstvi. A vseobecna verejnost ve stoletich pred i po tomto Newtonove epochalnim objevu brala gravitaci v dennim zivote jako danou vec, nad kterou se nikdo nepozastavoval. Ale nad jejim fungovanim se dodnes pozastavuji studenti fyziky, aspon ti kteri jeste na nerezignovali na porozumeni sveta a pro ktere ani Obecna teorie relativity neni tou pravou odpovedi. Ovsem musi si tu zvidavost nechavat pro sebe, s porozumenim se ve vedecke ani amatersko-vedecke komunite dozajista nesetkaji a jen riskuji posmech.
Fenomen setrvacnosti hmoty zustava dodnes hlubokou zahadou, na kterem si vylamal zuby jak Newton, tak Einstein (A. Pais - Einsteinuv zivotopisec, oznacil setrvacnost hmoty jako stale nevysvetlenou zahadu). Zajemci z rad novych a jeste naivnich studentu jsou odkazani na Macha a Sciamu, tedy na teorie majici jiz nejaky ten zub casu a ve ktere nikdo stejne nikdy neveril a ziji podnes jen proto, ze nikdo jiny po nich uz nikdy s nicim lepsim neprisel.
Imaginarni cislo 'i' vzbuzovalo odbornou polemiku az nekdy do poloviny minuleho stoleti, pak stari profesori vymreli a nove generace 'modernich vedcu' uz s nim zadne problemy nema, staci jim ze funguje, jako funguje gravitace a elektromagnetismus. A kdyz se obcas nejaky student po prvotnim seznameni s complexnimi cisly na to imaginarni cislo zepta, je mu receno, ze to vse je uz davno objasneno, ze ctverec imaginarniho cisla 'i' je proste zaporna velicina, a co jeste chtit vice... nefunguje snad neco? Nebo kde je problem? A vetsina studentu po pocatecnim nadseni pro vec skloni hlavy a volky nevolky zaradi se do stada, drive ci pozdeji.
Elektromagnetismus je ze stejneho soudku. Naprosta rezignace na hlubsi vysvetleni je na dennim poradku. Jen ti bystrejsi mezi vedci, jeste nezkorumpovani mezi studenty fyziky se obcas ptaji, jak to vsechno funguje a nejsou spokojeni s tradicnim vysvetlenim. Dobre to popsal napriklad R. Feynman ve svych znamych prednaskach, kde popisuje jak coby profesor vysvetluje zakum jak funguje elmag radiace a jak mava rukama kolem hlavy a pak machne jeste jednou naposledy a rekne - tak takhle nejak to funguje... ale sam vi, ze doopravdy nevi jak to funguje, ze vsechno to mavani rukama je jen neco jako cachry machry kouzelnika na jevisti provadene za ucelem odvedeni pozornosti, aby studenti nepoznali, ze doopravdy jim nic vysvetleno nebylo.
Vedci a zvlaste ti dnesni, moderni, jsou vubec machri v zametani problemu pod koberec, ve zjistovani, ze problemy minulosti byly vlastne pomylenymi otazkami, ze nahlednuto z jineho uhlu vlastne vubec zadny problem neni a nikdy nebyl, ze to vse byl jen vyplod nasi mysli - umele navozeny problem tam, kde vlastne nikdy doopravdy zadny nebyl.
Rekl bych, ze za nejaky cas to bude jak to tu pan Broz predvida a to i bez nejake kvantove hracky.
Postupem casu uklidime pod koberec i tu temnou hmotu a energii, zatim ovsem se na jejich vyzkumu moc dobre vydelava na to aby byly tyto pod nej zameteny, rezignace prijde az po nejake dalsi generaci vedcu s vylamanymi zuby mozkovych zavitu, kdy uz tyto jevy prestanou byti tak lukrativni zalezitosti pro vyzkum.
A co bysme vlastne chteli, dulezite je ze umime vypocitat ktera tlacitka a jak je mackat na te cerne bedynce, abysme obdrzeli zadanou odezvu. A ono to tak funguje a co jeste chtit vic, ze?
Tomáš Crhonek,2012-06-25 12:43:08
Vaclav Knowledge-integration:
Jak psal Brož, je třeba to brát pragmaticky. Pomocí imaginární jednotky se dobře počítá. Nic víc, nic méně. Osobně jsem to nikdy nebral jako záporný kvadrát ale jako jiné vyjádření vektorů (bod na ploše).
Šlo by to i pomocí vektorů. Nebo pomocí kvatermionů (btw Marwell psal v kvatermionech, později se to předělalo do vektorů pro snadnější počítání.).
Nebo úplně jinak s prostředky matematické analýzy. Tohle se mi líbí na teoretickém objevu antičástic. Dvěmi zcela různými cestami (braketový zápis - matice, a diferenciální počet) se přislo na stejný výsledek, tudíž teoretickou předpověď antičástic. Jsou to jen prostředky. Diferenciální počet má počátky u Newtona, který potřeboval matematický aparát pro popis silového působení.
Pragmatismus je nevedecky
Vaclav Knowledge-integration,2012-06-25 23:31:38
Kdyz neco funguje, tak me zajima, jak to funguje. Matematika baziruje na definicich a dukazech vseho, ale kdyz prijde na zakladni kameny, jako treba to imaginarni cislo, najednou jich netreba. Proste zaku, prijmi tento stavebni kamen analyzy komplexnich cisel na viru a vse pak z toho nasleduje uplne logicky. ;)
Akceptance, prijatelnost
Vaclav Knowledge-integration,2012-06-26 13:55:40
Mate to marne. Muzete hrackami otupit vetsinu lidi, ale vzdycky se nakonec najde nejaky jedinec, ktery polozi tu nesikovnou otazku, jak to vlastne funguje. Anebo dokonce prijde s nejakym novym modelem fungovani.
Pred Newtonem a jeho Principiou byli vsichni lide na svete otupeni gravitaci, nebyla to jen nejaka hracka pro vyvolene bohatsi obcany, ale byla uplne vsude a pro kazdeho, od toho nejvetsiho chudase az po krale, a byli na ni vsichni dokonale zvykli a brali ji jako samozrejmost, jako vzduch ktery dychaji. Ale pak prisel Newton a privolal k jevu gravitace pozornost a tato najednou ztratila svou odvekou samozrejmost. A lide se zacali ptat, jak to funguje, ze prece neni mozne aby na dalku pusobily nejake sily...
No a pak se lide na nejakych tri sta let museli spokojit s zadnym vysvetlenim a prezili to. A pak prisel Einstein se zakrivenym prostorem. I pote se kaciri podivovali a dodnes podivuji nad timto vysvetlenim, rikaji ze zakriveny prostor se da predstavit abstraktne ve dvou rozmerech, ale nedava to zadny smysl ve skutecnem trirozmernem svete. A nechapou vice veci ohledne toho zakriveneho prostoru. Ale nesetkavaji se s pochopenim, podobne jako se s nim nesetkali kaciri v post Newtonovskem svete. Jako tenkrat, jsou vytlaceni s tim, ze prakticky prinos teorie prebiji logiku modelu, jestlize tento ma nejake nedostatky jako ten Einsteinuv, anebo v post Newtonovskych casech, ze model neni vubec zadny.
Nasi predchudci vydrzeli be jakehokoli modelu gravitace tri sta let, my mame na konte tech let zatim jen nejakych sto. A uz ztracime trpelivost a prestavame doufat a snazime se problem vyhovujiciho modelu zamest pod koberec s tim, ze je to prece pomylene vubec chtit nejake vysvetlovaci modely, ze si mame zvyknout ze zadne vysvetleni neni a nebude, ze je pomylene vubec nejake chtit. Otazkou je, jak by to bylo byvalo s Einsteinovym zakrivenym prostorem, kdyby pred nim uz dve dlouha stoleti panoval nazor, ze model gravitace nejen ze neni, ale ani neni zadouci, ze modely vubec jsou nesmysl, ze si proste mame zvyknout na to ze gravitace funguje a pak nam ani neprijde se ptat, jak to funguje. Bude nam to proste jasne, odmalicka. A Einstein v takovem pripade by byl zesmesneny, ani by nestacil na jeho praci oschnout inkoust. Byl by to jen zaostaly a pomyleny bloud, jenz nepatri do vaznych vedeckych diskuzi - byly by mu predhozeny Faradayovy neviditelne pruzinky, cimz by mu bylo receno at zaleze do diry, kde je jeho misto... Asi jako je dnes bran kdokoli, kdo by napriklad oprasil eter absolutniho prostoru, nikdo by se ani nemamahal ho vyslyset, byl by odepsany predem. A tak, kdyby nasi predchudci nebyli tak trpelivi celych tri sta let, nemeli bysme dnes ani ten, byt nedokonaly, Einsteinuv zakriveny prostor.
ad Akceptance, prijatelnost
Ondřej Adamovský,2012-06-26 20:22:33
nemáte pravdu. Důvodem úspěchu teorie relativity bylo to, že Newtonovská fyzika měla některé nedostatky, které teorie relativity řešila. Praktizká měření skutečných jevů ukázala, že Enstein je pavdě blíž než Newton. Nebýt nesrovnalostí Newtonovy mechaniky s realitou, byla by Einsteinova teorie jen okrajovým myšlenkovým cvičením.
Fyzika zkoumá vztahy mezi pozorovanými jevy a v současnosti má největší úspěchy s pomocí matematických modelů těchto vztahů. Rozhodující je, zda model odpovídá realitě, a úsilí se upírá tam, kde jí neodpovídá.
Myslím, že to, co popisujete jako vysvětlení daného jevu, je ve skutečnosti intuitivní pochopení jevu, což je vlastně implicitní vytvoření nějakého modelu uvnitř mozku, takže člověk pak dochází ke správným výsledkům bez přemýšlení. Čím dále pokračujeme ve vytváření matematických modelů vesmíru, tím složitějšími se nutně tyto modely stávají, a tím těžší je dojít k intuitivnímu pochopení.
Lidé před Newtonem gravitaci intuitivně chápali jenom potud, pokud se týkala jejich bezprostředního okolí, tj. povrchu Země. Newton její působení rozšířil i na oblohu, a tam už její pozemské intuitivní chápání přestalo fungovat. Lidé nepřestali intuitivně chápat jak funguje gravitace na povrchu Země, jenom nezačali intuitivně chápat, jak funguje na obježné dráze.
Máte pravdu v tom, že existují dva hnací motory pokroku ve fyzice. Když rozumový, matematický, model odporuje pozorované skutečnosti, hledáme jeho vylepšení, nebo nový model, který v tomto rozporu nebyl. Když matematický model odporuje našemu intuitivnímu modelu, snažíme se buď intuitivně pochopit ten matematický, nebo přizpůsobit ten matematický našemu intuitivnímu. Tento druhý motiv má nejspíš větší potenciál převratných objevů, než ten první, bohužel je také více náchylný na trpká zklamání.
Pokud jsem vám, pane Václave Knowledge-integration svým "intuitivním modelem" podsunul vámi neakceptovatelnou interpretaci fyzikálního vysvětlení matematického modelu, pak se omlouvám. Jeví se mi jako nejlépe odpovídající.
Intuice
Vaclav Knowledge-integration,2012-07-02 23:18:48
My se pane Adamovský trochu mijime.
Pisete, ze "Duvodem úspechu teorie relativity bylo..."
V tom popisu uspechu te teorie mate pravdu, ale me slo o jinou vec. Kdyby totiz byl tehdy na prelomu devatenacteho a dvacateho stoleti jakykoli vysvetlovaci model pro seriozni vedu neprijatelny, pak by Einstein treba zavrhnul nejakou myslenku zakriveneho prostoru uz predem a ani by nezacal pracovat na tom matematickem modelu vseobecne teorie. A kdyby prece jen pokracoval a zaslal tu praci k publikaci, tak kdyby nebyl tak znamy na ucet predchozi prace (r1905), redaktori by ji jen zalistovali, uvideli by vyrazy 'zakriveny prostor' a utrpne by se usmali, rekli by si neco o 'Faradayovych pruzinkach' a bez dalsiho zkoumani by ji dale nevenovali pozornost, poslali by ji Einsteinovi zpet. Takze by vseobecna teorie vubec nemusela byt.
Vim ze tento priklad je trochu pritazeny za vlasy, ale prijatelnost neceho v te ktere dobe vseobecne hraje dost velkou roli v tom, jestli se nekdo necim tak kontroversnim vubec zacne zabyvat. Anebo kdyz zacne, jestli to pak da do placu na verejnost s rizikem, ze bude zesmesneny jeste pred tim, nez si nekdo vubec pozorne precte a zamysli se nad tou praci.
To se podle me stalo Newtonovi, ktery dlouha leta nic nepublikoval, zrejme z duvodu uzavrenosti tehdejsich vedeckych kruhu k 'novotam' (tenkrat jeste doznivalo stredoveke pojeti vedy, kdy popis zkoumane reality prijatelnych praci byl vice emotivni, nez rozumovy), a kdyz pak zacal publikovat a setkal se s sziravou kritikou z jistych kruhu, tak na to zanevrel a dalsi dekadu, ci jak dlouho zase nic nepublikoval az byl vyprovokovan k napsani 'Principie' a prolomil tak ledy k prijeti noveho pojeti fyziky. Ovsem i pote tezce trpel kritiku, ktera se zase vratila, ale byla aspon castecne prehlusena pozitivnim ohlasem na publikaci Principie.
Chci tu naznacit, ze geniove byvaji nesmeli (to se nijak nevylucuje napriklad s tou Newtonovou povestnou az spalujici kritikou vuci svym protivnikum), ze pokrok ve vedach byva dost krehka vec, ze prostredi odepisovani neceho uz dopredu, zesmesnovani, muze vest k zabiti pokroku, jeho oddaleni na prihodnejsi, pratelstejsi casy.
Dnes uz napriklad asi nikdo ani neusiluje o nejaky prijatelny vyklad kvantove mechaniky, naopak vychloubave vystavovani na odiv verejnosti absurdnosti stavajiciho vykladu se stava normou. Takze nyni mame atmosferu, ve ktere si vedci jiz ani nepreji, aby nedej boze nekdo neprisel s nejakym prijatelnym vykladem QM, protoze by jim to zborilo zamky jejich vychloubani, jak je clovek pred tou realitou bezmocny, ze ji nikdy nemuze prorozumet. A to je podle me obrazek zvrhlosti vedy. Moje argumentace pro optimismus v tomto smeru je vyvracovana, i zesmesnovana. A hledaji se vsechny mozne argumenty pro programovy pesimismus.
Takze se me nedivte, kdyz pouzivam i takove prirovnani jako napriklad tu stadnost. Zvlast pan Broz je velkym zastancem toho programoveho pesimismu dnesni vedy. Ale abych byl ferovy, to muze byt jen vyprovokovany postoj, a jsem si vedom toho, ze dost provokuji...
==================
"Myslím, že to, co popisujete jako vysvetlení daného jevu, je ve skutecnosti intuitivní pochopení jevu, což je vlastne implicitní vytvorení nejakého modelu uvnitr mozku, takže clovek pak dochází ke správným výsledkum bez premýšlení."
Vysvetlenim daneho jevu myslim jeho rozumove pochopeni, vysvetleni. Intuitivni porozumeni pak zavisi na tom rozumovem pochopeni toho ktereho daneho jevu (nebo z nej vyplyva). Intuice jako takova je vec (funkce) naseho podvedomi, a podvedomi je dlouhodobe formovane nasimi rozumovymi zavery, ke kterym jsme behem dosavadniho zivota dospeli, at uz jsou to zavery spravne, nebo nespravne, pomylene. Intuitivni porozumeni je tak neprimo odvisle od naseho rozumoveho porozumeni.
A podvedomi, intuice, funguje i v tech pripadech, kdy z ruznych duvodu si rozumove nedokazeme v tom kterem okamziku privolat do plneho vedomi vsechny ty rozumove duvody (pro ten ktery jev), ke kterym jsme kdy dospeli a proto pak dochazi k tomu, ze "clovek pak dochází ke správným výsledkum bez premýšlení".
Takze 'aby byla intuice', musi pred tim byt nejake rozumove pochopeni, i kdyz treba roztrousene v case na nejake dilci reseni nejakeho problemu. Podvedomi dokaze sesumirovat vsechny poznatky ke kterym jsme kdy na dane tema dospeli a posleze nam poskytne vysledek ve forme intuitivniho usudku (jehoz spravnost, ci nespravnost ovsem zavisi jak jsem uz rekl na spravnosti ci nespravnosti tech vedome prijatych kousku vedomosti v minulosti).
======================
Ohledne tech "dvou hnacích motoru pokroku ve fyzice."
Ten prvni rika, ze experiment je nadrazeny nasemu modelu. S tim nelze nez souhlasit.
K tomu druhemu muzu snad jen rici, ze "prizpusobit ten matematický našemu intuitivnímu" je pochybny, nebo aspon nedoporucovany postup, i kdyz nekdy muze vyjit.
Nemate to dobre napsane, ale neprijde me to jako zas tak dulezite. Ale stravil jsem nad tim dost casu, abych pak nakonec k tomu moc nenapsal.
Souhlas
Vaclav Knowledge-integration,2012-07-05 22:35:59
"Martin Plec 22.06.2012 v 14:29: Zároven si však myslím - asi na rozdíl od Pavla Brože - že snaha o nalezení prijatelné filozofické interpretace QM není pouhá kratochvíle, presto že se za to Nobelovka neudeluje. Protože pomáhá vytvorit model, ve kterém veškeré podivnosti QM budou vypadat prirozene, intuitivne a nebudou vzbuzovat neduveru, pochybnosti a odpor."
-
S timhle nazorem Martina Plece plne souhlasim.
---
"A i my amatéri, kterí matematiku za QM neznáme, si pak mužeme myslet, že jsme do principu QM aspon cástecne pronikli."
-
Veci se maji tak, ze ani znalost matematiky QM neumoznuje nejake proniknuti do prinicipu teto oblasti fyziky (minena jeji interpretace). Specialisti na QMechaniku jejim tajum nerozumi o nic vice, nez jim rozumi, nebo mohou rozumet vazni amatersti zajemci.
Experimenty v kvantove mechanice sice amaterum moc pristupne nejsou, anebo vubec, ale vzdycky se nakonec najdou sikovni popularizatori, kteri dokazi zajemcum s vaznym amaterskym zajmem vsechno docela dobre vysvetlit (hodi se ovsem znalost jazyku, hlavne Anglictiny).
A je plno 'poloamateru', kteri fyziku nebo jinou vedu studovali na urovni vysoke skoly a maji aspon poneti o pouzivane matematice a takovi muzou mit prakticky plnohodnotny nahled do kvantove mechaniky a maji prakticky stejnou vychozi pozici vypracovat nejakou interpretaci teto vedy, protoze takova prace zrejme nelezi v nejake specialni znalosti matematiky QM - protoze je jiste, ze kdyby nalezeni interpretace byla zalezitost matematiky, pak by specialisti davno uz s nejakou prijatelnou interpretaci davno prisli. Jenze tady se jedna o opravdovou Fyziku s velkym F, cili fyzickou interpretaci, fyzicky model. A na ty dnesni veda uz pomalu ani neveri a tak neni divu, ze se nam ve fyzice hromadi nevysvetlene experimentalni vysledky.
bob
Maroš Štulajter,2012-06-20 20:34:35
myslím že takým najdôležitejším v celej sústave je miesto ktoré vytvára bob, z daného fotónu vie identifikovať určitý stav ak ich máme viac každy vie identifikovať určité stavy pre rôzne veličiny vlnovej rovnice pomocou dvoch fotónov ktoré napr. môžu byť opačne polarizované. v danom prípade ich máme 4, tzn ak nám každý odovzdá 2 informácie zadanej vlnovej funkcie tak máme 8 qbitov. ale tak by mal vlastne fungovať aj qbitový počítač. ale aby sme mohli prenášať gbitové stavy musíme najprv poslať zadanie vlnovej funkcie. tak som to pochopil ja, opravte ma ak som napísal zle.
ad Tomáš B.
Václav Vincik,2012-06-20 18:57:36
Ty částice podle mě v tom neurčeném stavu jsou, anžto v okamžiku, kdy bys chtěl jejich skutečný stav měřit, zhroutí se vlnová funkce. Do té doby jsou v superpozici všech stavů.
0,000 nic 1 dílek momentu v ní zůstat nemůže. Spin je, jako ostatně prakticky všechno, kvantován. Takže pokud u jedné částice určíme spin 1/2, druhá z propleteného páru nemůže mít nic jiného než -1/2.
A to je celé kouzlo "teleportace".
V.Vincik
Tomáš Bartoň,2012-06-22 17:41:30
Jj, já vím že už probíhaly nějaké testy na existenci dalších skrytých proměnných a prozatím to spíš vypadá že nejsou, ale pořád mám problém s tím připustit že částice "sama sebe" vidí stejně "hloupě" jako my s našimi soudobými měřícími metodami :-)
Kde je chyba - v mereni, nebo jeho vykladu.
Vaclav Knowledge-integration,2012-07-10 14:13:12
“Tomáš Bartoň 22.06.2012 v 17:41
pořád mám problém s tím připustit že částice "sama sebe" vidí stejně "hloupě" jako my s našimi soudobými měřícími metodami :-) “
Nejde o nase merici metody, tedy o nejakou jejich nedokonalost, ale o spravnost vykladu vysledku toho mereni – ta je zrejme mylna.
Tomáš Skřivan,2012-06-20 16:40:00
Pokud to chapu dobre tak. To funguje tak ze Alice s Bobem maji kazdy svoji kulicku(ktera je cervena a zelena zaroven ale obe maji stejnou barvu(kdyz se na ni kouknou)). Ted Bob chce Alici poslat stribrno zlatou kulicku. Tak Bob si da obe kulicky do ruky a koukne se jakou maji barvu dohromady(proste se to nejak smicha). Tuhle barvu zatelefonuje Alici a Alice se znalosti teto barvy pak muze zachazet se svoji kulickou jako se zlato stribrnou(i kdyz byla cerveno zelena). A to by mela byt ta teleportace.
Ladislav Lang,2012-06-20 14:19:25
Trochu mi to připadá, jako kdybychom vzali dvě kuličky stejné barvy a aniž bychom se podívali jakou barvu mají, tak bysme tu jednu odnesli kilometr daleko. Pak bychom se podívali na tu první - byla by třeba červená a následně na tu druhou - a jaký to zázrak! Také je červená! "teleportace" prokázána.
Podle kvantové teorie měly celou dobu nějaké náhodné barvy a teprve v okamžiku pozorování obě zničehonic "zčervenaly". No nevím, asi budu (společně s panem Schrödingerem) dále k takové interpretaci skeptický.
Přesně
Tomáš Bartoň,2012-06-20 16:59:02
totéž si myslím od začátku. To, že nějakou částici uvedeme do "neurčeného" stavu, vůbec neznamená že v tom stavu doopravdy je, jenom to že se nám tak (teoreticky) jeví. Může v ní zůstat 0,000...libovolné množství nul...1 dílek převládajícího momentu, a ten prostě rozhodne jaký výsledek dostaneme při příštím měření. Takže de facto od sebe oddělujeme z "propleteného" stavu dvě přesně dané částice, akorát my o nich nevíme (resp. nemáme nástroj kterým bychom zjistili) že dané už jsou... :-)
Červená kulička
Vojtěch Kocián,2012-06-21 08:03:03
Pokud jsem to dobře pochopil, tak je na obě strany odelána "nějaká kulička". Když se na ni Alice podívá, tak zjistí, že je třeba červená. Pokud by se podíval Bob ještě předtím, než mu to Alice zatelefonuje, může zjistit, že je třeba zelená nebo červená se stejnou pravděpodobností. Teprve poté, co zjistí, že ta kulička má být červená, se na ni může podívat, aby zjistil, že opravdu červená je. Zjednodušeně, barva kuličky se v podstatě nezjišťuje, zjišťuje se výsledek její interakce s jinou částicí.
Není problém provést vyvracecí pokus, pokud by tomu někdo nevěřil.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce



