
Když budeme chtít co největší objem vtěsnat pod povrch s co nejmenší plochou, musíme zvolit tvar koule. Tak například 10 cm3 se vejde do koule s povrchem o rozloze 22,446 cm2, kdybychom ale volili krychli, hodnota by vzrostla na 27,849 cm2. Slabé vazby mezi polárními molekulami vody v beztížném stavu to nakonec hezky názorně dokumentují. Snímky astronautů hrajících si s poletujícími vodními „míčky“ jsou notoricky známé. Kapka představuje fyzikální soustavu v nejnižším energetickém stavu odpovídajícímu daným podmínkám. Bez vlivu gravitace má tvar koule.
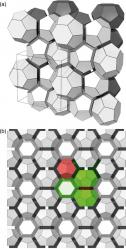
Jenže jaký tvar by měly mít bublinky pěny s nejnižší energií? Samozřejmě, že nemůže jít o seskupení kuliček. Tvar pěnových bublin snad jako první systematicky studoval belgický fyzik Joseph Plateau (1801 – 1883). Ještě za jeho života jeho známější britský kolega lord Kelvin definoval „dokonalou pěnu“ jako pravidelnou voštinovou soustavu stejně velkých buněk tvaru osmistěnu se seříznutými rohy. Takový prostorový geometrický tvar je ohraničen šesti čtvercovými a osmi šestiúhelníkovými plochami (obrázek vpravo). Tato představa pěny s nejnižší energií přetrvala až do roku 1994, kdy fyzik Denis Weaire spolu se svým doktorandem Robertem Phelanem z Trinity College v irském Dublinu našel matematické řešení pro strukturu s ještě nižší energií, i když jenom o 0,3 %. Již to nebylo seskupení zcela stejných buněk, ale kombinace 12stěnů a 14stěnů se stejným objemem (obrázek vlevo). Nové řešení, které bylo podle autorů pojmenováno Weaire-Phelanovou strukturou, představovalo jen teoretický model. Jak ho však zreálnit napěněním roztoku?

Zhmotnit matematický model v podobě konstrukce z pevného materiálu samozřejmě problém nebyl a Weaire-Phelanova struktura prý inspirovala tvůrce olympijského plaveckého stadionu Water Cube (Vodní kostka) v Pekingu (obrázek vpravo). Ale v bazénu uvnitř budovy by se ji nepodařilo vytvořit ani celému reprezentačnímu týmu Číny ani při tom nejusilovnějším tréningu, i kdyby jim do vody nalili hektolitr nejkvalitnější pěny do koupele. Nedařilo se ji napěnit ani v laboratorních podmínkách, dokud Weairův kolega Stefan Hutzler, šéf výzkumné skupiny pro pěnové a komplexní systémy z dublinské Trinity College nedošel na to, že chyba je v nádobě. „Ideální“ pěna se totiž nemůže vytvořit v prostoru ohraničeném rovnými plochami, které okrajové bublinky deformují, což se pak promítá do celého objemu. Musí se jim podstrojit správná forma. Malou krabičku s pěti vhodně tvarovanými stěnami (obrázek dole vpravo) vědci vytvořili z průhledného polymeru pomocí 3D tiskárny a počítačového programu. Tak bublinkám pěny poskytli trojrozměrný návod pro správný tvar. Velikost bublinek do požadovaného průměru 2,4 mm regulovali pomocí velikosti kapiláry a tlaku dusíku, jenž přes ní vypouštěli do připraveného roztoku běžného mycího prostředku na nádobí. Jak do formy bubliny zachytávali, dokumentuje následující video – pro pochopení experimentu stačí část mezi 2:55 a cca 4:00. Výslednou pěnu tvořenou asi 1 500 bublinkami nafotili. Makrosnímky odhalily bezchybnou Weaire-Phelanovou strukturu. Tentokráte však byla reálná a ne jen na obrazovce počítače.
Video: Příběh Weaire-Phelanovy struktury v podání dvou spoluautorů práce, Stefana Hutzlera a Denise Weaire z Trinity College v Dublinu. Jak ji lze vytvořit, když máte vhodnou trojrozměrnou šablonu, odhaluje část mezi 2:55 a 3:58.

Najde zatím nejefektivnější forma pěny uplatnění v praxi? Těžko odhadnout. Kdyby se podařilo zvládnout její formování z různých kapalin – i z tavenin, pak bezpochyby. Znamenala by úsporu materiálu tam, kde se dnes používají kovy nebo plasty s odlehčenou a deformaci pohlcující pěnovou strukturou. Další možnou aplikací by mohly představovat různé výměníky tepla a vědci zmiňují i fotonické krystaly.
Kdo první porazil Kelvina?
Při vyhledávání informací lze na internetu natrefit na neočekávaná fakta. Ken Brakke z Katedry matematiky na Susquehanna University v Pennsylvanském Selinsgrove zveřejnil na své stránce kopii dvoustránky z knížky Linuse Paulinga The Nature of the Chemical Bond (Vlastnosti chemické vazby), kterou vydalo nakladatelství Cornell University v roce 1960. Nakreslená struktura jednoznačně odpovídá té Weaire-Phelanově z roku 1994. Ken Brakke, který se sám snažil najít energeticky efektivnější řešení, než nabídl lord Kelvin, k tomu s povzdechem dodává: „Tato kniha stála v knihovně mého otce tři metry ode mne v době, kdy jsem se okolo roku 1991 snažil „porazit“ Kelvinovu pěnu. Kdybych ji tenkrát otevřel na stránce 471, jsem přesvědčen, že bych souboj o vítězství nad Kelvinem vyhrál.“
| Hezké makrofoto pěny z běžného přípravku do koupele. Autor André Karwath snímek poskytl Wikipedii. Celý záběr zde. | Pěnu obvykle tvoří velmi rozmanité bublinky. Kredit: Osel.cz |
Diskuze:
souvislosti
Pavel Brejcha,2012-02-06 14:07:20
zajímavé, obvzlášt v souvislosti s informací, že náš vesmír je topologicky nejspíš 12-ti stěn a s Lindeho úpravou inflační teorie (mnoho vesmírů jako pěna).
osmisten?
Jergy jergy2,2012-02-05 15:36:22
no... nechcem byt vrtak, ale jak pocitam, tak pocitam furt mi na tom obrazku vychadza desatsten.
pokud máte na mysli to Kelvinovo řešení
Pavel Brož,2012-02-05 16:26:08
tj. ten obrázek s popiskem "Lord Kelvin spočítal, že ...", tak tam je opravdu osmistěn se seříznutými rohy, tedy ve výsledku čtrnáctistěn (protože výchozí osmistěn má šest vrcholů - rohů - a jejich seříznutím přidáte šest dodatečných stěn).
Mimochodem, stejný čtrnáctistěn dostanete i tak, pokud za výchozí tvar nevezmete osmistěn, ale krychli, a vhodně jí seříznete rohy. Krychle má šest stěn a osm rohů, jejichž seříznutím dostanete opět celkových čtrnáct stěn. Pouze musíte ty rohy seříznout dostatečně hodně, abyste místo trojúhelníkových dodatečných plošek dostali šestiúhelníkové, teprve pak bude výsledný čtrnáctistěn tvořený šesti čtverci a osmi šestiúhelníky, jako je na tom již zmíněném obrázku uprostřed (ten zelený čtrnáctistěn).
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce





