Špeciálna teória relativity viedla vedcov k presvedčeniu, že nijaký hmotný objekt ani informácia sa nemôžu pohybovať rýchlejšie ako svetlo vo vákuu. Začiatkom šesťdesiatych rokov sa však začalo uvažovať o tachyónoch, časticiach pohybujúcich sa rýchlejšie ako svetlo. Možnosť ich existencie vyplýva zo vzorcov teórie relativity, no doteraz sa nepodarilo experimentátorom ani jeden tachyón zachytiť. Viac o týchto hypotetických časticiach si povieme teraz.
V predchádzajúcom článku sme uviedli jednoduchý dôkaz tvrdenia, že rýchlosť hmotných telies nemôže prekročiť rýchlosť svetla vo vákuu c. Vychádzali sme z relativistického vzťahu pre energiu častice, ktorá má kľudovú hmotnosť m0 a rýchlosť v.
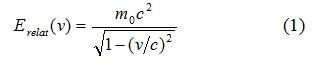
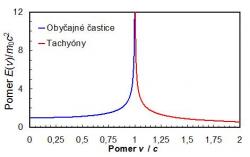
V menovateli vzťahu (1) je odmocnina, ktorej hodnota sa s približovaním rýchlosti telesa k rýchlosti svetla1 neustále zmenšuje. V prípade, že v = c, je hodnota tejto odmocniny nulová. Energia pohybujúceho sa telesa preto s rýchlosťou rastie a v bode v = c dosahuje nekonečnú hodnotu (Obr. 1). Modrá krivka na obrázku 1 vyjadruje relativistickú závislosť energie obyčajného telesa (častice) od jeho rýchlosti. Ak si predstavíme, že tento graf znázorňuje kopec, tak urýchľovanie telesa je ako jeho tlačenie do kopca. Ako sa blížime k rýchlosti svetla (pomer v/c sa blíži k 1), výška kopca začína prudko rásť a v bode v = c je kopec nekonečne vysoký. Takže nie je možné urýchliť ani najmenšiu časticu s nenulovou hmotnosťou na rýchlosť svetla, pretože by sme k tomu potrebovali nekonečnú energiu.
Odsúdení byť rýchlejší ako svetlo
Fyzici Bilaniuk, Deshpande a Sudarshan začiatkom 60. rokov minulého storočia ukázali, že samotná špeciálna teória relativity (ŠTR) pripúšťa existenciu hmotných objektov pohybujúcich sa rýchlejšie ako svetlo. Je potrebný len jeden smelý predpoklad. Analyzujme ešte raz vzťah (1) pre energiu telesa. Výraz pod odmocninou v menovateli sa stane menším ako 0, keď rýchlosť telesa prekročí rýchlosť svetla c (platí totiž v/c > 1). No a odmocnina zo záporného čísla je číslo rýdzo imaginárne2 (viď Matematická poznámka pod článkom). Energia každého hmotného telesa by sa tak pri prekračovaní rýchlosti svetla prehupla cez nekonečnú hodnotu do hodnôt imaginárnych. Keď však má fyzikálna veličina imaginárnu hodnotu nemôžeme ju v našom svete pozorovať. Obyčajné teleso preto nemôže mať rýchlosť väčšiu ako svetlo.
Spomínaná trojica predpokladala, že existujú telesá s imaginárnou hmotnosťou m0 (ktoré neskôr boli nazvané tachyónmi) a sledovali aké vlastnosti by im ŠTR prisúdila. Energia tachyónov by bola imaginárna pri rýchlostiach menších ako rýchlosť svetla. V takomto prípade máme vo vzťahu (1) imaginárnu hmotnosť v čitateli a obyčajné reálne číslo v menovateli (odmocnina je teraz reálna). Ak by rýchlosť tachyónov prekročila rýchlosť svetla, odmocnina vo vzťahu (1) by sa stala imaginárnou. Podiel dvoch imaginárnych čísel je číslo reálne (Matematická poznámka), čiže energia tachyónov by bola reálna pre rýchlosti väčšie ako c.
Závislosť energie tachyónov od ich rýchlosti je na obrázku 1 znázornená červenou čiarou. Vidieť, že čím je rýchlosť tachyónu väčšia, tým má menšiu energiu. Energia nekonečne rýchleho tachyónu bude nulová. Naopak, keď rýchlosť tachyónu klesá smerom k rýchlosti svetla, jeho energia sa stáva nekonečnou. Pri brzdení je potrebné tachyónu dodávať energiu. Pri urýchľovaní by energiu odovzdával – presne opačne je to pri obyčajných časticiach.
Ak teda pripustíme možnosť existencie častíc s imaginárnymi kľudovými hmotnosťami, môžeme všetky možné typy častíc rozdeliť do troch skupín (viď tabuľka):
- obyčajné častice – hmotnosť je reálna. Pohybujú sa len rýchlosťami menšími ako svetlo. Ich energia by vzrástla nad všetky medze, ak by dosiahli rýchlosť svetla. Pri rýchlostiach väčších ako rýchlosť svetla by sa ich energia stala imaginárnou, čiže v tejto oblasti rýchlostí nemôžu existovať,
- fotóny – hmotnosť je nulová. Vo vákuu sa môžu pohybovať len rýchlosťou svetla. Pri spomalení alebo zrýchlení by okamžite zanikli (ich energia by bola nulová),
- tachyóny – hmotnosť je imaginárna. Pohybujú sa len rýchlosťami väčšími ako svetlo. Aby sme ich spomalili na rýchlosť c, museli by sme im dodať nekonečnú energiu. Pri rýchlostiach menších ako rýchlosť svetla by bola energia tachyónov imaginárna, preto v tejto oblasti rýchlostí nemôžu existovať.

Rozdelenie častíc podľa ich kľudovej hmotnosti m0.
Zavedením tachyónov sa zmenil aj náš pohľad na rýchlosť svetla. Tú môžeme vnímať ako hranicu nepriechodnú ani z jednej strany. Obyčajné častice ju nemôžu prekonať smerom od nižších rýchlostí. Tachyóny ju zasa neprekonajú smerom od vyšších rýchlostí. Kým obyčajné častice sa nemôžu pohybovať rýchlejšie ako svetlo, tachyóny sú odsúdené na večné uháňanie rýchlosťami väčšími ako c.
Imaginárna hmotnosť tachyónov nemusí nikoho desiť. Tachyóny sa totiž od okamžiku svojho vzniku musia pohybovať rýchlejšie ako svetlo. Ich energia je preto reálna a kladná (ako sa na energiu patrí). Aby ste mohli pozorovať efekty imaginárnej hmotnosti tachyónov, museli by ste ich spomaliť na rýchlosť menšiu ako je rýchlosť svetla, na čo by ste potrebovali nekonečnú energiu.
Kde hľadať tachyóny?
Zo všetkých známych častíc len pri neutrínach zostala určitá šanca, že sú tachyóny. Existuje ale možnosť, že tachyóny objavíme vo forme dosiaľ nepozorovaných častíc. Niektoré strunové teórie napríklad obsahujú tachyóny ako základné stavy. Tieto stavy sú však nestabilné a sú z teórií eliminované vhodnými postupmi. My zostaneme radšej pri zemi a budeme sa venovať neutrínam.
Existujú tri druhy neutrín: elektrónové, miónové a tau neutríno. Sú to najslabšie interagujúce častice a s inými časticami „komunikujú“ len prostredníctvom slabej interakcie. Tá ale pôsobí na veľmi krátke vzdialenosti (len v rámci elementárnych častíc) a je extrémne slabá. Na ilustráciu uvedieme, že neutríno preletí cez bežnú hmotu v priemere desať miliónov miliárd kilometrov, kým vstúpi do interakcie s nejakou časticou! Táto vlastnosť neutrín je zodpovedná za všetky problémy, ktoré s nimi máme.
Len niekoľko rokov vieme, že neutrína majú nenulovú kľudovú hmotnosť. Experimenty, založené na sledovaní oscilácií neutrín (akým je práve experiment OPERA – pozn. red.), však umožňujú určiť len kvadrát rozdielu hmotností medzi jednotlivými druhmi neutrín (kvadrát imaginárneho čísla je číslo reálne – viď Matematická poznámka). Preto nevieme určiť presnú hmotnosť neutrín. V tejto oblasti sme odkázaní na starý spôsob stanovenia ich hmotnosti pomocou sledovania β-rozpadu vhodných atómových jadier (vznikajú pritom neutrína) v pozemských zdrojoch. Tieto experimenty však zatiaľ nedosahujú dostatočnú presnosť. Pri niektorých dokonca vychádzajú výsledky, podporujúce hypotézu o tachyónovských neutrínach. Štatistické a systematické chyby sú však zakaždým príliš veľké a tak nevieme s dostatočnou istotou rozhodnúť, či neutrína sú, alebo nie sú tachyónmi. Hoci novšie výsledky zmiernili problém s ich možnou imaginárnou, stále sa pri analýze výsledkov objavujú nezrovnalosti. Aby sme mohli pri takýchto typoch meraní presne zistiť hmotnosti neutrín, museli by sme aspoň o rád zlepšiť presnosť.

Merať priamo rýchlosť neutrín je ešte komplikovanejšie. Registrujeme len neutrína s vysokou energiou, takže ak by boli tachyónmi, ich rýchlosť by prekonávala rýchlosť svetla len o milióntiny percenta (čím má tachyón väčšiu energiu, tým bližšia je jeho rýchlosť k rýchlosti svetla). Pomocnú ruku by nám mohol podať výbuch blízkej supernovy. Pri takejto udalosti vznikajú obrovské množstvá neutrín. V roku 1987 vybuchla supernova vo Veľkom Magellanovom oblaku. Dva detektory vtedy zaregistrovali 20 neutrín 3 hodiny pred prvým svetelným zábleskom zo supernovy. To ešte nič neznamená, pretože neutrína opúšťajú vybuchujúcu hviezdu skôr ako fotóny. Presvedčivým dôkazom by bolo, ak by k nám doleteli nízko energetické neutrína skôr ako tie s vysokou energiou. Zaznamenaných neutrín ale bohužiaľ bolo príliš málo. Najpravdepodobnejšia je hypotéza, že neutrína prišli v dvoch skupinách (zrejme vznikli v dvoch fázach) a v týchto skupinách prišli energetickejšie neutrína skôr. Čiže opačne než by sa patrilo pri tachyónoch. Ale štatistická váha takejto interpretácie je malá. Ak by v súčasnosti nastal výbuch supernovy v našej Galaxii, zaznamenali by detektory niekoľko tisíc neutrín. To by stačilo na presnejšie zistenie ich hmotnosti, a teda aj na potvrdenie alebo vylúčenie možnosti, že sú tachyónmi.
Zaujímavým dôsledkom tachyónovej povahy neutrín by bol samovoľný rozpad protónov na neutróny. Rozpadali by sa len protóny s energiou väčšou ako istá medzná hodnota, ktorá by závisela od hmotnosti neutrín. Doteraz sa však takýto rozpad nepotvrdil. Ak by bol tento proces reálny, prejavilo by sa to určite v zložení kozmického žiarenia - prúdu častíc s veľmi veľkou energiou, dopadajúci na Zem z vesmíru. Malo by pozostávať prevažne z protónov. Neutróny sú totiž nestabilné a rozpadajú sa na protóny. Častice kozmického žiarenia letia k Zemi tisíce a milióny rokov a za tak dlhú dobu by sa mali prakticky všetky neutróny rozpadnúť. Predpovedaný rozpad protónu za účasti neutrína by ale celú situáciu zmenil, pretože protóny a neutróny by sa cyklicky premieňali jeden na druhý, a tak by sme na Zemi mali v kozmickom žiarení registrovať podstatne viac neutrónov, než sa predpokladá. Pretože však zaznamenávame spŕšku sekundárnych častíc vznikajúcich po zrážke častice kozmického žiarenia s časticou zemskej atmosféry, odlíšiť pôvodný protón od neutrónu je veľkým problémom.
Predpoklad, že neutrína sú tachyóny, by úplne prirodzene vyriešil jeden z problémov spojený s objavom hmotnosti neutrín. Doteraz boli pozorované len ľavotočivé neutrína. Pri takomto type častíc má ich spin (môžeme ho, aj keď nepresne, spojiť s rotáciou častice okolo osi) vždy opačný smer ako je smer ich pohybu. Vysvetlenie tohto faktu je triviálne, ak by neutrína mali nulovú hmotnosť. V tom prípade by sa pohybovali rýchlosťou svetla a nebolo by možné ich predbehnúť. Ak totiž predbehnete rotujúcu časticu, smer jej rotácie budete vidieť stále rovnaký, no smer jej pohybu voči vám sa zmení (zrazu poletí smerom od vás a nie k vám). Takže po predbehnutí by ste ľavotočivú časticu videli ako pravotočivú. Ak by neutrína boli tachyóny, situácia sa nezmení. Pohybovali by sa ešte rýchlejšie ako svetlo a všetko by bolo zachránené. Ak je hmotnosť neutrín nenulová, môžu mať aj menšie rýchlosti ako rýchlosť svetla. Mali by sa preto pozorovať aj pravotočivé neutrína. Zatiaľ sme ich však neobjavili. Aj na to však existujú vhodné vysvetlenia, ktoré však tachyónovskú povahu neutrín nepredpokladajú.
Takáto je teda súčasná (2006 – pozn. red.) situácia s hľadaním tachyónov. Pravdepodobnosť, že sú nimi neutrína, sa síce znižuje, ale zatiaľ ju celkom vylúčiť nemôžme. Väčšina fyzikov sa už nadobro otočila tejto špekulatívnej myšlienke chrbtom, no nádej niektorých ešte celkom nezomrela.
Poznámky:

Pozn. 1: Slovné spojenie „rýchlosť svetla vo vákuu“ budeme skracovať na „rýchlosť svetla“, prípadne namiesto dlhých slov použijeme len značku tejto rýchlosti c.
Pozn. 2: Namiesto termínu „rýdzo imaginárne“ budeme používať termín „imaginárne“, pretože tu budeme narábať len s rýdzo imaginárnymi číslami a nemôžeme sa preto pomýliť.
Pôvodný článok je uverejnený na stránke Physics.sk a bol prevzatý so súhlasom autora.
Zaujímavé odkazy:
O tachyónoch fyzici uvažovali už v 60. rokoch:
Olexa-Myron Bilaniuk & E. C. George Sudarshan: Particles Beyond the Light Barrier; Physics Today 1969
Teóriu relativity, ktorá ich popisuje, nazvali „meta-relativita“
Diskuze:
PRINCIP RELATIVITY
Rosa Palo,2011-10-28 06:40:30
Plati princip relativity aj pre fotony a tachyony ? Ak elektron vyzaruje fotony s rychlostou U(f) = c tak relativna rychlost "elektronu vzhladom k fotonu" by mala byt U´(e)= -U(f) = -c podla principu relativity aj podla principu reciprocity, ze V = -V´... Elektron by mal byt na svetelnom kuzeli "vzhladom k fotonu"... Je "PHOTON FRAME" nonsens aj v QED?
Dokaze QED zodpovedat aka je relativna rychlost fotonov po rozpade pozitronia? Je c alebo 2c ? PODLA FEYNMANA v clanku "Reason for antiparticles" sa v QED musia uvazovat vsetky rychlosti v < c aj v > c
ak plati CPT-symetria...
DAKUJEM za vsetky doterajsie aj pripadne dalsie diskusne prispevky R.P.
tu anihiláciu
Maroš Štulajter,2011-10-16 10:46:22
elektrón pozitrón som mal na mysli. ešte jeden príklad na skladanie rýchlosti, na elektróne ktorý vystrelíme z bodu A a budeme mu dodávať rýchlosť tak pri určitej energii začne vyžarovať fotóny ktoré majú s pohľadu pozorovateľa v bode A rýchlosť svetla a na tom môžme zistiť že fotón oproti aj keď mal rýchlosť trebars 0,99c tak bude len spomaľovať bude mu fotóny odoberať energiu, lebo fotóny budú síce mať rýchlosť c ale ich energia bude veľká, ono keď si predstavíme že hmotnosť je prepojená s energio podľa einsteina tak keď môžme si hmotu predstaviť ako energiu reprezentovanú fotónmi, fotón má síce nulovú pokojovú hmotnosť ale má energiu reprezentovanú vlnovou dĺžkou.
lorentzové transformácie
Maroš Štulajter,2011-10-14 15:31:35
vyplývajú s toho že rýchlosť svetla je konštantná, mňa ani nezaujíma či sa dá prekročiť alebo ako je to pri súčte rýchlostí pri rýchlostiach bližiacich sa "c", mňa zaujíma skôr fyzikálne určenie rýchlosti "c". v tom príspevku som sa zle vyjadril totižto ak mám nejakú najvyššiu hodnotu ktorú nemôžem prekročiť a dosiahnem ju v časovej zmene ktorá sa najviac blíži k nule (nie je 0)tak teleso by malo mať hmotnosť ktorá by sa najviac blížila k 0.
Pavel Brož,2011-10-14 22:00:33
Takhle, ve speciální relativitě mohou existovat tělesa, které mají nenulovou klidovou hmotnost (klidová hmotnost se značí často m0, zatímco dynamická hmotnost se obvykle značí jen m), a tělesa, která mají nulovou klidovou hmotnost.
Důležité je vědět, že klidová hmotnost je konstanta, zatímco dynamická se mění v závislosti na rychlosti (pro tělesa s nenulovou klidovou hmotou) či obecněji na hybnosti (závislost na hybnosti je použitelná i pro tělesa s nulovou klidovou hmotou).
Pro energii E tělesa v závislosti na hybnosti p platí vztah:
(1) E^2 = p^2 c^2 + m0^2 c^4
Tento vztah se speciálně pro tělesa s nulovou klidovou hmotou zjednoduší na vztah:
(2) E = p c
Tento druhý vztah tedy platí např. pro fotony.
Pro tělesa s nenulovou klidovou hmotou lze odvodit i zmíněný vztah závislosti jejich energie na rychlosti v:
(3) E = m0 / odmocnina (1 – v^2/c^2)
Tento vztah není použitelný pro tělesa s nulovou klidovou hmotou, pro ně lze použít pouze vztah E=pc. Pokud je hodnota m0 kladné reálné číslo, je tento vztah použitelný pro podsvětelně se pohybující částice; pokud je m0 imaginární číslo, pak lze vztah (3) použít pro nadsvětelně se pohybující částice. Nejde ale použít pro částice pohybující se rychlostí světla.
Nyní k Vaší otázce. Ze vztahu (3) je vidět, že pokud chcete urychlit těleso s nenulovou klidovou hmotou na rychlost světla, musíte dodat nekonečnou energii. Je přitom naprosto jedno, jestli v nějakém okamžitém procesu, anebo jestli během nějakého krátkého času. Jediné, co je zde důležité, je že na začátku má těleso podle vztahu (3) konečnou energii, a ve výsledku by podle tohoto vztahu mělo mít energii nekonečnou. Z toho samozřejmě plyne, že nelze žádné těleso s nenulovou klidovou hmotností urychlit (ani zpomalit v případě nadsvětelných částic) na rychlost světla.
Podobně nelze žádné těleso pohybující se světelnou rychlostí (tj. mající nulovou klidovou hmotnost) zpomalit na rychlost světla (ani urychlit nad rychlost světla). Protože světelnou rychlostí se může pohybovat pouze těleso s nulovou klidovou hmotností, jeho zpomalením na podsvětelnou rychlost (nebo urychlením na nadsvětelnou rychlost) bychom pak k určení jeho energie mohli použít vztah (3) – jenže z tohoto vztahu bychom dostali pro energii tělesa nulu. Tělesa s nulovou celkovou energií neexistují.
Proto žádná částice nemůže být urychlena z podsvětelné rychlosti na rychlost světla, ani zpomalená z nadsvětelné rychlosti na rychlost světla, aniž by zároveň došlo ke skokové změně klidové hmotnosti – jenže to je právě ten proces přeměny částic. Existují reálné procesy, při kterých se částice mající podsvětelné rychlosti mění na jiné částice pohybující se rychlostí světla, anebo naopak. To jsou anihilační a kreační procesy, ve kterých se např. podsvětelně se pohybující elektron a pozitron anihilují za vzniku dvojice fotonů, anebo kdy se dvojice dostatečně energetických fotonů přemění na pár elektron a pozitron. Beze skokové změny klidové hmotnosti ale žádný přechod mezi podsvětelným, světelným a nadsvětelným regionem není možný.
ďakujem za vynikajúce vysvetlenie
Maroš Štulajter,2011-10-13 12:56:03
pri mojej úvahe som zabudol na jednú vec že teleso pri okamžitej zmene na hocijakú konečnú konštantu potrebuje nekonečnú energiu môžme to urobiť ak máme nulovú hmotnosť a neutríno má hmotnosť.
Pavel Brož,2011-10-13 18:44:32
Bohužel, s Vaším tvrzením výše nelze souhlasit - pokud si tedy Vaše tvrzení vykládám správně jako "těleso při okamžité změně rychlosti na libovolnou konstantní rychlost potřebuje nekonečnou energii". Tam není důležitá okamžitost té změny. Jak speciální teorie relativity, tak Newtonova mechanika, nezakazují okamžité změny rychlosti. Rozdíl mezi nimi je v něčem trochu jiném:
V Newtonově mechanice můžete těleso urychlit okamžitě na libovolnou konečnou rychlost, a potřebujete na to vždy jenom konečnou energii. Okamžitá změna rychlosti tam nastává modelově např. u srážek nekonečně tuhých těles, anebo srážek hmotných bodů. Např. popis pohybu biliárových koulí lze ve velmi dobré aproximaci popisovat pomocí okamžitých změn jejich rychlostí při rázu. Žádná nekonečná energie k tomu není potřeba.
Ve speciální teorii relativity lze ukázat, že idealizace nekonečně tuhého tělesa vede k vnitřním logickým sporům, nekonečně tuhá tělesa jsou tedy ve speciální teorii relativity nepřípustná. Nicméně Idealizace hmotných bodů i ve speciální relativitě stále přípustná je, žádné logické spory tam nevznikají, a stejně tak je možné okamžitě měnit rychlosti hmotných bodů při jejich srážkách (nemusí to být jenom srážky, mohou to být i rozpady).
Ten skutečný rozdíl mezi speciální relativitou a Newtonovou mechanikou tkví ve skutečnosti v tom, že v Newtonově mechanice při dodání dostatečně velké, byť konečné energie, může mít těleso finálně libovolně velkou rychlost. Ve speciální relativitě, ať už dodáte tělesu pohybujícímu se podsvětelnou rychlostí, libovolně velikou energii, tak finálně získáte těleso, jehož rychlost se pouze o něco více přiblíží rychlosti světla, ale nikdy ji nepřekročí. Abyste urychlil těleso na rychlost přesně rovnou rychlosti světla, musíte mu dodat nekonečně velkou energii.
Úplně totéž se dá v teorii relativity ukázat, pokud jako výchozí máme těleso pohybující se nadsvětelnou rychlostí, a chceme ho zpomalit na rychlost rovnou přesně rychlosti světla. Paradoxně mu musíme opět dodat energii, ačkoliv ho zpomalujeme, a to energii opět nekonečnou.
Mezi podsvětelným a nadsvětelným sektorem ale existuje ještě jeden zásadní rozdíl. Pokud by totéž těleso, které by se na začátku pohybovalo podsvětelnou rychlostí, se mělo nějakým skokem octnout ve finálním stavu s nadsvětelnou rychlostí (aniž by se přitom ocitlo v mezistavu, kdy by mělo světelnou rychlost), tak by se jeho energie stala z počáteční kladné hodnoty hodnotou čistě imaginární. To také plyne z Lorentzovy transformace. Tzn. že měl-li by platit zákon zachování energie, musela by se počátečnímu tělesu nějakým způsobem dodat komplexní hodnota energie. Což je fyzikální nonsens. Ten by se dal obejít jenom tak, že by se rychlost částice změnila skokově z podsvětelná na nadsvětelnou a to tak, že by se během této okamžité změny měnila částice na nějakou jinou, která by v nadsvětelném sektoru měla reálnou, nikoliv imaginární energii. Taková částice by naopak v podsvětelném sektoru musela mít imaginární energii.
Takže čistě hypoteticky, máme-li částici s reálnou energií v podsvětelném sektoru, v nadsvětelném by měla energii imaginární. Máme-li částici s reálnou energií v nadsvětelném sektoru (hypotetický tachyon), měla by imaginární energii v podsvětelném sektoru. Jediný způsob, jak se dostat z podsvětelného sektoru do nadsvětelného či naopak, je udělat to skokem (tedy bez plynulé změny rychlosti z podsvětelné na nadsvětelnou či naopak), a zároveň při té skokové změně změnit typ částice.
To je také důvod, proč se i v rámci speciální teorie relativity mohlo bezesporně uvažovat o tom, že by neutrina mohly být těmi hypotetickými tachyony. Neutrina, stejně tak jako jakékoliv jiné částice, totiž vznikají a zanikají v procesech srážek a rozpadů částic, a tyto srážky a rozpady jsou v rámci kvantové teorie pole (=teorie elementárních částic) považovány za bodové procesy. Proto teoreticky neexistuje žádný spor se speciální teorií relativity, pokud by se podsvětelnou rychlostí se pohybující neutron rozpadl na proton, elektron a antineutrino, přičemž proton a elektron by se pohybovaly podsvětelnou rychlostí a antineutrino nadsvětelnou. Ostatně i z tohoto důvodu se už dříve mohlo spekulovat o tom, že by neutrina mohly být tachyonmi, což např. Vladimír Wagner popsal v jeho výborném článku zde: http://hp.ujf.cas.cz/~wagner/popclan/neutrina/neutrina.html
Problém je v tom, že pokud jsou výsledky Opery správně, tak neutrina nemohou být těmi tachyony, které jsou hypoteticky přípustné ve speciální teorii relativity, protože v rámci speciální relativity nelze dát do souladu výsledky z Opery s výsledky pozorování třeba ze supernovy SN1987A. Pokud jsou výsledky Opery správně, tak neutrina narušují Lorentzovskou invarianci. Což by mělo velké důsledky pro celou fyziku.
Myslím, že jsem Vás zmátl ve své předchozí reakci tím důrazem na plynulost toho zrychlování. Chtěl jsem tím zdůraznit, že s pomocí elektromagnetického pole (např. při urychlování částic v urychlovači) ani gravitačního pole (např. částice spirálovitě padající na černou díru) nelze podle speciální teorie relativity urychlit podsvětelně se pohybující částici na nadsvětelnou rychlost. Na přeměny částic v důsledku jejich rozpadů nebo srážek se ale toto omezení striktně vzato nevztahuje.
doplním triviálnu otázku
Maroš Štulajter,2011-10-12 20:55:53
prečo sa elmg. žiarenie vo vákuu zobralo ako najvyššia rýchlosť "c" keď tu máme častice ktoré ignorujú el. náboj. vo všetkom o fotóne je mi jasné ale nie je mi jasné či sa pri určovaní "c" myslelo aj na časticu ktorá ignoruje el. náboj ak bude niekto ochotný odpovedať na moje dotazy budem rád.
ad rychlost c
Pavel Brož,2011-10-13 00:09:01
Ta situace je z matematického hlediska velice jednoduchá - je to otázka, zda jsou všechny fyzikální zákony invariantní vůči Lorentzově transformaci, anebo zda některé z nich nejsou. Tou invariancí se myslí to, že když se prostorové souřadnice a čas transformují podle nějaké transformace, tak že forma těch zákonů zůstane táž. To potom automaticky způsobí, že mezi soustavami, které jsou mezi sebou spjaty právě tou příslušnou transformací, nemůžete vybrat žádnou privilegovanou pomocí zákonů, které jsou vůči té transformaci invariantní, protože pozorovatelé v obou soustavách mohou právě tu svou považovat za privilegovanou.
Situace by se samozřejmě změnila, pokud bychom měli vůči nějaké transformaci invariantní jenom nějaké zákony, ale jiné ne, anebo kdyby ty jiné byly invariantní vůči jiné transformaci, ale ne vůči té původní. Takhle přesně ta situace vypadala v druhé polovině devatenáctého a pár let na začátku dvacátého století. Mělo se za to, že elektrodynamika, určená Maxwellovými rovnicemi, je invariantní vůči Lorentzovým transformacím, zatímco mechanika je invariantní vůči Galileiho transformacím. Díky tomu bylo teoreticky možné najít privilegovanou, absolutní klidovou soustavu. Tato soustava by se dala poznat podle toho, že pouze v ní by současně platily jak Maxwellovy rovnice, tak rovnice Newtonovy mechaniky. Pokud bychom se z této absolutní klidové soustavy transformovali do jiné, pohybující se soustavy pomocí Galileiho transformace, Newtonovy zákony by si zachovaly svou formu (tudíž čistě jen podle nich bychom neuměli rozhodnout mezi starou a novou soustavou, která z nich je privilegovaná), nicméně Maxwellovy rovnice už by měly jinou formu – přešli by do jiných rovnic. Analogicky, pokud bychom z původní absolutní klidové soustavy přešli do jiné, pohybující se soustavy, pomocí Lorentzovy transformace, tak by si naopak Maxwellovy rovnice zachovaly svou formu (a tudíž bychom pomocí jen čistě elektromagnetických jevů nemohli rozhodnout o privilegovanosti mezi původní a novou soustavou), nicméně zase Newtonovy zákony by přešli do jiného tvaru.
Suma sumárum, máme-li některé zákony invariantní vůči Galileiho transformaci a jiné vůči Lorentzově transformaci, pak z toho automaticky plyne existence jedné význačné soustavy, ve které všechny fyzikální zákony mají nějakou privilegovaný tvar. Naopak pokud jsou úplně všechny zákony invariantní buď jen vůči Galileiho transformaci, nebo všechny jen vůči Lorentzově transformaci, tak žádnou privilegovanou soustavu (alias éter) nelze najít.
Hypotéza éteru byla postavena na předpokladu, že některé zákony (Newtonova mechanika) jsou invariantní vůči Galileiho transformaci, zatímco zákony Maxwellovy elektrodynamiky vůči Lorentzově transformaci.
Naopak z postulátů speciální teorie relativity automaticky vyplývá, že všechny fyzikální zákony musí být invariantní vůči Lorentzově transformaci.
Vraťme se do doby, kdy se věřilo éterové hypotéze. Logickým důsledkem byly pokusy najít onu privilegovanou soustavu. Ta se měla dát najít tak, že pouze v ní se světlo mělo pohybovat rychlostí c, která se dala vypočíst z permitivity vakua a z permitivity vakua, tj. ze dvou konstant figurujících v Maxwellových rovnicích. Rychlost c tehdy nebyla v žádném případě považována za nějakou limitní rychlost. Byla to pouze rychlost, která z Maxwellových rovnic určovala, jako rychlostí se světlo pohybuje v absolutní klidové soustavě. V jakékoliv jiné soustavě se světlo mělo pohybovat rychlostí buď menší než c, anebo větší než c. Galileiho transformací bylo teoreticky možné přejít do soustavy, ve které se světlo nepohybuje, anebo naopak do soustavy, ve které se světlo pohybuje klidně rychlostí miliónkrát větší než c – žádný problém zde z hlediska Galileiho transformací nevznikal.
Problém se ale objevil, když se rychlost světla měřila v různých, vůči sobě se pohybujících soustavách. Pokud bychom se totiž vůči éteru pohybovali rychlostí v, pak se měla naměřit ve směru šíření světla jeho rychlost jakožto c-v, zatímco v opačném jako c+v, přesně tak, jak to předpokládá Galileiho transformace. Jenže oproti všem očekáváním se naměřila rychlost světla vždy stejná, v libovolně se pohybující soustavě, vždy rovná konstantě c.
Po mnoha a mnoha analýzách začalo být jasné, že je nutné začít dělat modifikace v Newtonově mechanice. Čistě hypoteticky bylo možno také chtít modifikovat naopak Maxwellovy zákony, a nechat Newtonovy zákony nezměněny. Maxwellovy zákony jsou ale extrémně citlivé vůči modifikacím – přesněji řečeno, elektromagnetické děje jsou enormně citlivé. Tato citlivost je dána mj. právě tou obrovskou hodnotou rychlosti c (teď mám na mysli velikost té konstanty, ne velikost rychlosti světla, která podle Galileiho transformace mohla být libovolně zvýšena či snížena). Elektromagnetické děje jsou velmi rychlé (proto se ve druhé polovině devatenáctého století komunikace přenášela elektricky pomocí telegrafu, na mechanicky), a v důsledku této enormní rychlosti se také dají mnohem snáze konstruovat extrémně citlivé měřící elektrické přístroje – tak např. elektrický proud se už v té době dal měřit s mnohem lepší relativní přesností, než jakákoliv mechanická veličina. Proto se stalo prakticky okamžitě jasným, že to nebudou Maxwellovy rovnice, které se budou měnit, ale že to budou s mnohem menší přesností ověřené zákony Newtonovy mechaniky (navíc v té době neexistoval žádný pokus, ve kterém by mechanické děje probíhaly relativní rychlostí byť jen částečně se blížící rychlosti světla – ve světě elektrických a magnetických jevů naopak nebyl nejmenší problém takové děje běžně pozorovat a měřit).
Mechanické zákony začaly být postupně modifikovány, krok za krokem. Cílem mělo být umět vysvětlit, proč se přes všechny seberafinovanější pokusy nedaří najít absolutní klidovou soustavu – éter. Tj. proč rychlost světla ve všech možných soustavách vychází rovna konstantě c, a nikoliv proč není v různě se vůči sobě pohybujícím soustavám různá (tj. rovná c-v anebo c+v, pokud se v absolutní klidové soustavě pohybujeme rychlostí v ve směru šíření světla, anebo v protisměru).
Nakonec, dalo by se říci v předvečer uvedení speciální teorie relativity, začalo být zřejmé, že všechny zákony Newtonovy mechaniky mají tvar formálně invariantní vůči Lorentzově transformaci. Použil jsem slovo „formálně“, a to protože se tehdy nevěřilo, že souřadnice získané Lorentzovou transformací udávají skutečné souřadnice platné v druhé, vůči té původní pohybující se soustavě. Místo toho se stále lpělo na víře, že jediné správné souřadnice jsou dané Galileiho transformací, ačkoliv v té době už ve fyzice nezbyl snad jediný zákon, který by vůči Galileiho transformaci zůstal invariantní. Prakticky všechny zákony už byly přepsány do podoby, která byla invariantní vůči Lorentzově transformaci.
Nyní už se konečně mohu vrátit k Vaší otázce. Limitní rychlost c totiž automaticky plyne právě z té Lorentzovy transformace. Takže otázka je postavena tak, jestli ty které zákony vyhovují Lorentzově transformaci, anebo ne. Pokud vyhovují Lorentzově transformaci, tak čistě matematickým odvozením lze exaktně (a nijak složitě) dokázat, že pokud se příslušné těleso, které se podřizuje těmto zákonům invariantním vůči Lorentzově transformaci, pohybuje podsvětelnou rychlostí, tak k jeho urychlení na rychlost světla bychom potřebovali nekonečnou energii. Čistě formálně lze také ukázat, že pokud bychom měli těleso pohybující se naopak nadsvětelnou rychlostí, tak bychom k jeho zpomalení přesně na rychlost světla potřebovali tomuto tělesu také dodat nekonečnou energii.
Z pohledu Lorentzovy transformace existují tři absolutně od sebe oddělené regiony rychlostí – region podsvětelné rychlosti, region světelné rychlosti, a region nesvětelné rychlosti. Vlastnosti Lorentzovy transformace pak striktně zakazují přecházet jakémukoliv tělesu z jednoho regionu do druhého procesem plynulého urychlování či zpomalování, obecněji pak procesem plynulého dodávání či snižování energie.
Mimochodem, kvantová teorie díky svým „skokovým“, pravděpodobnostním procesům, disponuje teoretickým potenciálem pro obejití tohoto omezení. Tak např. vypařování černých děr je možno vysvětlit několika ekvivalentními způsoby, přičemž jeden z nich se dá popsat jakožto protunelování částice z vnitřku černé díry ven. Bez kvantových jevů by k tomu, aby se částice dostala z pod horizontu černé díry ven potřebovala docílit právě té nadsvětelné rychlosti. Nicméně musím zdůraznit, že vypařování černých děr, ačkoliv je dnes přijímáno jakožto teoreticky velice uspokojivě vysvětlený děj, v žádném případě nelze považovat za důkaz toho, že se částice mohou pohybovat nadsvětelnou rychlostí. Vypařování černých děr je komplexní proces, který se popisuje docela složitým matematickým aparátem, přičemž pro tento proces můžeme konstruovat různé „interpretace“, které nám podávají jakýsi zjednodušující pohled na to, co tam probíhá. Těchto interpretací, které podávají tentýž výsledek, přitom existuje více, a interpretace používající nadsvětelnou rychlost je jen jedna z nich. Žádná z těchto názorných interpretací nám přitom neumožní nic konkrétního spočítat; pokud chceme získat nějaké číselné výsledky, musíme interpretace hodit za hlavu a vrátit se k abstraktnímu matematickému aparátu.
Takže souhrnem – rychlost šíření elektromagnetického záření ve vakuu se nevzala slepě jakožto největší dosažitelná rychlost. Mělo se za to, že i elektromagnetické záření se může pohybovat rychlostí větší než c. Jenže se EXPERIMENTÁLNĚ zjistilo, že tomu tak není, že rychlost elektromagnetického záření JE ROVNA konstantě c ve všech soustavách. Tzn. že toto není nějaké teoretické dogma, toto je výsledek experimentu. Následně se ukázalo, že další a další zákony je nutno přepsat do podoby invariantní vůči Lorentzovým transformacím. Lorentzovy transformace si už pak samy vynutí to, že existují tři od sebe oddělené regiony rychlostí – podsvětelný, světelný a nadsvětelný. Rychlost daná konstantou c je limitní v tom smyslu, že žádná částice z podsvětelného regionu nemůže být plynule urychlena na světelnou či nadsvětelnou rychlost dodáním konečné energie (naopak žádná z podsvětelného nemůže být plynule zpomalena na světelnou či podsvětelnou rychlost ani plynulým dodáváním, ani plynulým odebíráním konečné energie).
Platnost Lorentzovy invariance pro všechny známé fyzikální zákony se ověřovala ve statisících experimentů přes více než sto let, zatím vždy úspěšně. Pokud se potvrdí výsledky neutrinových měření OPERY, tak by to s největší pravděpodobností znamenalo, že jsme poprvé narazili na fyzikální zákon, pro který Lorentzova invariance neplatí. Protože na Lorentzově invarianci je postavena prakticky celá moderní částicová fyzika, ale také třeba astrofyzika, kosmologie, atd., tak skutečnost, že by byť jen dílčí fyzikální zákon, konkrétně ten, podle nějž se řídí neutrina, nebyl Lorentzovsky invariantní, měl docela dalekosáhlé důsledky. Naznamenalo by to konec speciální teorie relativity, ale i tak by to znamenalo velice výrazné rozšíření této teorie, srovnatelné s tím, jakým rozšířením byla právě speciální teorie relativity pro Newtonovu mechaniku.
triviálna otázka
Maroš Štulajter,2011-10-12 13:46:12
vidím že sa v diskusii pokračuje tak ja by som mal jednu otázku. prečo pre elmg vlnenie do ktorého patrí svetlo zaviedlo pre jeho určenie el. veličiny. z rovnice nám vyplýva že "c^2" je vlastne konštanta sily priťahovania el. nábojov v prostredi kde je najväčší mg. odpor pri konštante prevrátenej mg. vodivosti.
Zrádná aplikace spec. relativity pro v>c
Jan Vít,2011-10-11 15:22:34
Lorentzovy transformace byly odvozeny pro subluminální rychlosti a nelze je aplikovat pro v>c. Protože pro v>c jde čas v jedné soustavě pozorovaný z druhé soustavy zřejmě obráceně, je nutno vyjít z rovnic x’ = gama(x + vt), x = gama(x’ – vt’), x = ct, x’ = –ct’ (při použití obvyklé symboliky).
Odtud dostaneme gama=c/(v+c), což je reálné číslo. Superluminální spec. teorie relativity potom vypadá odlišně od obvyklých předpokladů.
ale kdepak
Pavel Brož,2011-10-11 17:15:09
Bohužel evidentně nevíte, o čem Lorentzova transformace je, a stejně tak nazdařbůh dosazujete do vzorečků, které z hlediska odvození Lorentzovy transformace nemají žádný význam.
Je více způsobů odvození Lorentzovy transformace, jeden je postaven na tom, že se jedná o transformaci zanechávající invariantní Maxwellovy rovnice, jiný třeba na tom, že ponechávají invariantní kvadratickou formu x^2-c^2*t^2, existují ještě další ekvivalentní způsoby. Směr toku času v nich nehraje žádnou roli. Všechny jsou pak singulární pro v=c, bez ohledu na to, z které strany se k c blížíte, ať už z rychlostí podsvětelných či nadsvětelných. Vy dostáváte naopak ze svého vzorečku pro v=c konečnou transformaci s koeficientem gama=c/(v+c)=c/2c=1/2, což je evidentně nonsens.
Zrádná aplikace spec. relativity pro v>c
Jan Vít,2011-10-11 15:16:09
Lorentzovy transformace byly odvozeny pro subluminální rychlosti a nelze je aplikovat pro v>c. Protože pro v>c jde čas v jedné soustavě pozorovaný z druhé soustavy zřejmě obráceně, je nutno vyjít z rovnic x’ = γ(x + vt), x = γ(x’ – vt’), x = ct, x’ = –ct’.
hrana signálu
Maroš Štulajter,2011-10-06 22:10:29
tiež si myslím že najpravdepodobnejšou príčinou je určenie štart signálu, len ma zaráža že je to až o min 60 ns a prečo za 3 mesiace sa to nepreverilo tak že skutočne by sa dalo povedať že je to chyba. nehovorili vaši kolegovia čo by mohlo spôsobiť že nastala taká veľká chyba pri kalibrácii a prečo to bolo teraz keď s podobnými energiami pracovali už skôr.
Takové experimenty se dělají poprvé
Vladimír Wagner,2011-10-06 23:43:13
Vážený pane Štulajer, takové experimenty se ještě nedělaly. Máte start a stop signál v místech vzdálených stovky kilometrů, navíc nemůžete provést časovou kalibraci příslušného protonu k příslušnému neutrinu (vůbec nevíte, který proton (vzniklý mezon) jej způsobil. Mohl to být kterýkoliv z toho 10,5 mikrosekundového pulsu. To není vůbec jednoduché sesynchronizovat. A když přesnou příčinu daného posuvu nenašli, tak to není nic triviálního. Já si bez znalostí technických podrobností netroufám odhadovat vůbec, kde je zdroj toho posunu. Nejsem na to takový expert.
verím cernu.
Maroš Štulajter,2011-10-06 14:49:52
najprv. by som chcel poďakovať za vynikajúci príspevok od pána Broža, zatiaľ je to najlepší príspevok aký som čítal na webe. prečítal som si veľa článkov o pokuse v cerne a o neutrínach, konkrétne čo som našiel o posledných pokusoch ako prebiehajú merania. používajú metódu na fázového posuvu tvaru protónového impulzu pri vytvorení tvaru neutrínami podľa energie, tvar impulzu na opere je identický ako tvar impulzu protónov, len je posunutý o určitý čas spôsobený odozvou merania a časom preletu neutrín. pre rýchlosť svetla je naplánovaný cca. 1045 ns a impulz došiel o 60 ns skôr. toto je overené od roku 2008 takže štatistická chyba je minimálna ak vôbec nejaká je. myslím si že bude treba str. doplniť.
Není to tak jednoduché
Vladimír Wagner,2011-10-06 18:47:50
Vážený pane Štulajtere, věc není tak jednoduchá. Měření probíhala sice od roku 2008, ale velikost statistické chyby nezávisí na době nabírání, ale na tom, kolik neutrin se podařilo zachytit. A to bylo celkově za ty dva a půl roku pouze 16 111 neutrin. Ta byla rozložena po délce pulsu 10,5 mikrosekundy. Navíc byly dvě různé extrakce, každá s jiným tvarem. Takže i statistická chyba určení tvaru a hlavně počátku pulsu neutrin není určitě zanedbatelná. Jak je ostatně vidět i z obrázku, který jsem přebral z původní publikace do článku pro Osla: http://www.osel.cz/popisek.php?popisek=18006&img=1317312412.jpg Jsou tam vyznačeny právě i statistické nejistoty. Pochopitelně tvar pulsu protonů je určen velice přesně (těch se na těch 16 000 neutrin muselo urychlit 10^20) - viz červená čára v obrázcích. Bližší popis je pak v tom mém článku a pochopitelně daleko lepší v původní publikaci. Podstatná je přesnost určení tvaru, který má nesrovnatelně větší statistickou chybu, tedy neutrinového pulsu.
Navíc ještě větší nejistota je skrytá v systematických chybách při časové kalibraci, navázání časů v CERNu a Gran Sasso a určení start a stop signálu. Mluvil jsem nedávno s několika kolegy, kteří se dobře znají s lidmi s OPERY a s příslušnými experty a ti snad vidí nejpravděpodobnější zdroj chyby ve tvaru a určení hrany signálu, který definuje start. Ale to je zatím jen jedna s více možností.
Jinak s Vámi souhlasím, že příspěvek Pavla Brože je skvělý. Pavel Brož je podle mě nejlepší z autorů, kteří kdy pro Osla psali. Má také na svědomí nejlepší a myslím i nejčtenější článek (o temné hmotě), který tu vyšel.
musím se bránit :-)
Pavel Brož,2011-10-06 21:55:41
Nemohu přijmout být označen za nejlepšího autora na oslu, napsal jsem zde jenom snad dva popularizační články (plus jeden recesistický :-)) Nejlepším autorem je podle mě jednoznačně Jaroslav Petr, který kdysi psal stovky článků pro osla, vlastně kvůli jeho článkům jsem osla objevil a začal pak pravidelně číst. Samozřejmě je tady také ohromné množství výborných článků Josefa Pazdery a dalších autorů, včetně Vás. Právě Vaše články obsahují bezkonkurenčně největší množství konkrétních údajů, takže třeba články o Fukušimě byly nedostižným zdrojem velice precizních informací.
Autoři Osla
Vladimír Wagner,2011-10-06 23:51:55
Jarda Petr je úplně renesanční osobnost a píše toho hodně a perfektního, škoda, že už teď ne pro Osla. Také kvůli němu chodím rád na redakční rady Vesmíru. Je potěšením ho tam poslouchat s jeho fantastickým přehledem nejen o novinkách ve vědě. A souhlasím, že je řada dalších výborných autorů na Oslovi. Kromě jmenovaných třeba Dáša. A určitě Standa Mihulka. Bez něj by Osel tedy totálně prořídnul. A bude moc fajn, když se další objeví. Takže vyzývám tímto, pište.
verím cernu.
Maroš Štulajter,2011-10-06 14:49:49
najprv. by som chcel poďakovať za vynikajúci príspevok od pána Broža, zatiaľ je to najlepší príspevok aký som čítal na webe. prečítal som si veľa článkov o pokuse v cerne a o neutrínach, konkrétne čo som našiel o posledných pokusoch ako prebiehajú merania. používajú metódu na fázového posuvu tvaru protónového impulzu pri vytvorení tvaru neutrínami podľa energie, tvar impulzu na opere je identický ako tvar impulzu protónov, len je posunutý o určitý čas spôsobený odozvou merania a časom preletu neutrín. pre rýchlosť svetla je naplánovaný cca. 1045 ns a impulz došiel o 60 ns skôr. toto je overené od roku 2008 takže štatistická chyba je minimálna ak vôbec nejaká je. myslím si že bude treba str. doplniť.
verím cernu.
Maroš Štulajter,2011-10-06 14:46:20
najprv. by som chcel poďakovať za vynikajúci príspevok od pána Broža, zatiaľ je to najlepší príspevok aký som čítal na webe. prečítal som si veľa článkov o pokuse v cerne a o neutrínach, konkrétne čo som našiel o posledných pokusoch ako prebiehajú merania. používajú metódu na fázového posuvu tvaru protónového impulzu pri vytvorení tvaru neutrínami podľa energie, tvar impulzu na opere je identický ako tvar impulzu protónov, len je posunutý o určitý čas spôsobený odozvou merania a časom preletu neutrín. pre rýchlosť svetla je naplánovaný cca. 1045 ns a impulz došiel o 60 ns skôr. toto je overené od roku 2008 takže štatistická chyba je minimálna ak vôbec nejaká je. myslím si že bude treba str. doplniť.
pre pána Výmolu
Maroš Štulajter,2011-10-05 22:05:43
súhlasím že einstein nemusel poznať neutrálne leptóny teoria relativity je správna ale nikola tesla poukázal na to že "c" ako najväčšia rýchlosť nie je správna, ale vo vzorcoch funguje. to by mohol byť aj prípad s tými neutrínami. pozeral som na webe funkciu merania časov pre rýchlosť neutrín, porovnávajú sa tvary impulzov protónov, a impulzu ktoré vypracuje opera s energie neutrín ak je dĺžka impulzu menšia tak je rýchlosť väčšia ako c
Re
Vít Výmola,2011-10-05 22:42:55
Tady dochází k určitému omylu, ale je to častý omyl. To, že je c nejvyšší možnou rychlostí není chybným předpokladem STR. To, co je tím předpokladem je KONSTANTNÍ rychlost světla, bez ohledu na pozorovateli nebo vzájemných pohybech. Einstein teorií relativity tuto podivnost vysvětluje: Aby c bylo konstantní, musí platit to a to. A je to pak vyjádřeno nějakými vzorci STR. A teprve z nich vyplývá, že rychlost c je nejvyšší možná. Pokud by tomu z jakéhokoliv důvodu nebylo, tak je celá teorie relativity špatně. Zároveň by se ovšem muselo najít jiné vysvětlení konstantního c. To totiž není žádný výmysl, konstantní c vyplývá z Maxwellových rovnic a byla ověřena experimenty.
Ta situace je trochu komplikovanější.
Pavel Brož,2011-10-06 01:47:44
Einstein konstantní rychlost c v speciální teorii relativity postuloval, nikoliv vysvětloval.
Stejně tak je nutné říct určitá "ale" k tvrzení, že konstantní c vyplývá z Maxwellových rovnic. Ze samotných Maxwellových rovnic, pokud k nim nepřidáme Einsteinovy postuláty, na nichž Einstein vystavěl svou speciální teorii relativity, totiž konstantní rychlost světla neplyne.
Před vznikem Einsteinovy teorie relativity existovaly dvě odlišné dynamiky - Newtonova mechanika hmotného bodu a kontinua, a Maxwellova elektrodynamika. První z nich byla v souladu z Galileiho principem relativity (přesněji řečeno, dnes jej tak zpětně nazýváme, abychom jej odlišili od Einsteinova principu relativity). Galileiho princip relativity říkal, že když přejdeme z nějaké inerciální pozorovací soustavy, do jiné inerciální soustavy (všechny inerciální soustavy se vůči sobě musí pohybovat rovnoměrně přímočaře), tak že forma fyzikálních zákonů se nezmění. Tudíž mezi všemi možnými vůči sobě se rovnoměrně přímočaře pohybujícími inerciálními soustavama nelze žádným způsobem vybrat nějakou preferovanou. Tj. nelze definovat žádný absolutní prostor, který by byl v klidu a který by definoval význačnou stojící soustavu, zatímco všechny jiné soustavy by mohly být absolutně určeny svou rychlostí vůči tomuto absolutnímu prostoru.
Ve skutečnosti právě zmíněná Galileiho relativita platí pouze pro tu první z obou dynamik, tj. pro Newtonovu mechaniku (bez ohledu na to, jestli vezmeme Newtonovu mechaniku hmotného bodu anebo Newtonovu mechaniku kontinua).
Po nějaké době po odvození Maxwellovy elektrodynamiky začalo být zjevné, že Maxwellovy rovnice nevyhovují Galeleiho relativitě, které vyhovuje Newtonova mechanika. Z Maxwellových rovnic přitom vyplývala existence elektromagnetických vln (světlo jsou přitom elektromagnetické vlny mající specifické frekvenční rozmezí), šířících se rychlostí c. Tato rychlost c se dá v rámci Maxwellovy elektrodynamiky získat jako převrácená hodnota z odmocniny součinu permitivity vakua a permeability vakua. Tolik lze říct k tvrzení, že hodnota c vyplývá z Maxwellových rovnic.
Bohužel z Maxwellových rovnic samotných nijak nevyplývá, že by se světlo mělo šířit rychlostí c v JAKÉKOLIV inerciální soustavě. Místo toho se ve druhé polovině devatenáctého století a během několika let na začátku století dvacátého věřilo, že pomocí Maxwellových rovnic, potažmo pomocí měření rychlosti světla v různých inerciálních soustavách, budeme moci zjistit význačnou stojící klidovou inerciální soustavu, alias absolutní prostor, alias éter. Éter byla hypotetická materie, jejíž vibrace se projevují jakožto elektromagnetické vlny, podobně jako když se vibrace hmotného prostředí (plynu, kapaliny, pevné látky), projevují jako zvuk.
Hypotéza éteru byla celkem logická, zvláště, když se zpočátku vůbec nevědělo, že by se světlo mohlo pohybovat tak neuvěřitelně, že jeho rychlost bude ve všech inerciálních soustavách stejná. To se totiž zdálo odporovat zdravému rozumu, a normálním každodenním lidským zkušenostem se to zdá odporovat dodnes. Dodnes totiž všichni bereme jako samozřejmost, že když se vůči nám pohybuje vagón rychlostí třeba 20 km/h, a cestující ve vagóně jde rychlostí 5 km-h ve směru jízdy, tak že se vůči nám stojícím na nástupišti pohybuje ruchlostí 25 km/h. Podle Galileiho principu relativity se one cestující vůči nám rychlostí 25 km/h opravdu pohybuje, ale podle Einsteinova principu relativity ne, podle něj se vůči nám pohybuje rychlostí malilinko menší, než je 25 km/h.
Vycházejíc z celkem logické hypotézy éteru bylo logickým následujícím krokem měření rychlosti světla v různých inerciálních soustavách za účelem zjištění význačné inerciální soustavy, ve které éter stojí. Byl to opravdu veliký šok, když i přes opakovaná všemožně alterovaná měření vycházelo, zdravému lidskému rozumu navzdory, že světlo má vůči svému zdroji rychlost stejnou bez ohledu na pohyb soustavy, v níž se zdroj světla nachází. Analogie k pohybu cestujícího ve vlaku by byla taková, že vlak se výči nám pohybuje rychlostí c, a když cestující v něm do té doby sedící vystartuje rychlostí c ve směru pohybu, bude se vůči nám stojícím na nástupišti pohybovat stále rychlostí c. A pokud místo ve směru pohybu vyrazí v protisměru (takže bychom čekali, že se vůči nám pohybovat nebude, neboť rychlost pohybu cestujícího by se měla odečíst od rychlosti pohybu vlaku), tak se oproti našemu očekávání vůči nám stále budem pohybovat rychlostí c. A pokud by se cestující ze zoufalství nechal vystřelit z vlaku libovolným směrem, např. by se katapultoval kolmo nahoru rychlostí c, tak se oproti našemu očekávání vůči nám bude pohybovat stále rychlostí c.
Pokud toto někomu nepřijde zvláštní, tak ve skutečnosti o speciální teorii relativity nikdy nepřemýšlel. Nicméně ačkoliv toto skládání světelných rychlostí, které dává paradoxně stejný výsledek c bez ohledu na soustavy, vypadá sebevíce podivně, tak právě toto bylo na základě měření rychlosti světla opakovaně experimentálně potvrzeno.
Samozřejmě vznikla potřeba, jak s tímto výsledkem naložit. Brzy se našla fenomenologická vysvětlení v podobě tzv. Fitzgeraldovy kontrakce. Éteru byla přisouzena dodatečná vlastnost, která měla způsobit, že když se nějaká hmotná látka vůči němu pohybuje, měla se ve směru pohybu zkracovat. Tato kontrakce délek měla vysvětlovat, proč rychlost světla vycházela numericky stejně ve všech soustavách. Podobně se zjistilo, že jindy je pro vysvětlení jiných měření nutno transformovat kromě délek i časové intervaly. Přechodem k novému, zvláštním způsobem transformovanému systému, který se vůči původnímu nejen pohyboval, ale který měl také speciálním způsobem škálované délky a časové intervaly, bylo možné převést Maxwellovy rovnice vyjádřené v původní soustavě, do úplně stejné formy těchto rovnic v oné nové soustavě.
Ta podivná transformace zahrnující i škálování délek a časových intervalů se nazývá po svém objeviteli Lorentzovou transformací. Záhy se ukázalo, že Lorentzova transformace znamená pro Maxwellovy rovnice naprosto totéž, co znamená Galileiho transformace pro Newtonovu mechaniku. Galileiho transformace ponechává formu Newtonových zákonů tutéž, když z původní soustavy přejdeme pomocí Galileovy transformace do jiné pohybující se soustavy (říkáme, že Newtonova mechanika je vůči Galeleiho transformaci invariantní). Podobně Lorentzova transformace ponechává invariantní Maxwellovy rovnice.
Čistě jen pomocí Newtonovy mechaniky nebylo možné objevit žádnou význačnou inerciální soustavu právě v důsledku Galileiho relativity. Stejně tak nelze čistě jen pomocí Maxwellových rovnic najít žádnou význačnou soustavu v důsledku Lorentzovy invariance Maxwellových rovnic.
Pokud se ale vezmou obě dynamiky dohromady, Newtonova i Maxwellova, tak potom tam žádná společná invariance není - Newtonova dynamika změní svou formu při Lorentzových transformacích, zatímco Maxwellova dynamika změní formu při Galileiho transformacích, takže formálně nemělo být problém význačnou soustavu objevit. Jenže právě to se nedařilo, ony Fitzgeraldovy kontrakce totiž způsobovaly právě to, že vše se v hmotném pohybujícím se prostředí smrsklo právě tak, že nešlo nic naměřit. To ostatně nebyl takový div, protože tyto kontrakce byly právě takto vymyšleny. Co ale následně začalo být opravdu mrzuté, bylo to, že se nedařilo najít žádný alternativní způsob, jak najít jakýkoliv fyzikální děj, který by se těmto kontrakcím vymykal, anebo pomocí kterého by se dal vliv těchto kontrakcí potlačit. Kdyby se takový děj našel, zámek střežící tajemství éteru by byl odemčen.
Mezitím se stále věřilo, že Galileiho transformace je ta pravá, která nám říká, jak se souřadnice v pohybujících se soustavách transformují. O tom nebylo dlouhá léta žádných pochyb, ostatně, bylo to v souladu s naší každodenní zkušeností. Všechny paradoxy speciální teorie relativity ve skutečnosti vypovídají právě o tom, že naše každodenní zkušenost s pomalu se pohybujícimi se objekty (pomalu ve srovnání s rychlostí světla, tzn. v reálu všechny hmotné objekty, se kterými přicházíme během celého našeho života skrze naše vlastní smysly do přímého kontaktu) se nedají extrapolovat do světa rycjlostí srovnatelných s rychlostí světla.
No a když se tedy věřilo, že Galileiho transformace je ta pravá, tak co se mínilo o Lorentzově transformaci? O ní se věřilo, že dává pouze jakési fiktivní, pomocné souřadnice, ve kterých se jakousi matematickou hříčkou zachovává forma Maxwellových rovnic, nicméně které ale nelze chápat jakožto skutečné souřadnice měřící skutečné délky a čas. Toto si po dlouhou dobu myslel jak sám Lorentz, tak Poincaré, kterého bychom dost možná měli pokládat za skutečného otce speciální teorie relativity. Poincaré, ale nejen on, totiž odvodil drtivou většinu relativistických dynamických zákonů ještě před Einsteinem.
Když tedy byla většina relativistických dynamických zákonů objevena ještě před Einsteinem, tak jakto, že je za objevitele speciální teorie relativity považován Einstein, a ne Lorentz či Poincaré?
Rozdíl je v interpretaci právě těch souřadnic. Lorentz i Poncaré považovali za pravé (skutečné) pouze souřadnice získané na základě Galileiho transformace. Podle této transformace mají elektromagnetické vlny, tudíž i světlo, rychlost c pouze v soustavě stojící vůči éteru. V soustavě pohybující se vůči té první rychlostí v se pak světlo šíří rychlostí c+v, nikoliv rychlostí c. To, že je experimentálně změřena rychlost šíření světla jaožto c nezávisle na pohyb soustavy, bylo Lorentzem a Poincarem chápáno ne jakožto prvotní vlastnost světla, ale jakožto jakési nedopatření působené těmi Fitzgeraldovými kontrakcemi. Maxwellovy rovnice měly v pohybujících se soustavách jinou formu, než ve stojící soustavě, což bylo v rámci Lorentzova a Poincareho paradigmatu naprosto v pořádku. Lorentzově transformaci, která na rozdíl od Galileiho ponechávala Maxwellovy rovnice invariantní, byl přisuzován význam pouhého matematického kuchtění, na základě kterého lze získat jakési fiktivní souřadnice, ve kterých jakousi náhodou vypadá dynamika stejně, jako v těch originálních, skutečných souřadnicích.
Staré paradigma ale začínalo povážlivě erodovat právě s postupně se kupícími se vzorečky, které postupně modifikovaly původní Newtonovu mechaniku do dnešní relativistické dynamiky. Do roku 1904 už vlastně chyběl jeden jediný čistě Einsteinův relativistický vztah = E=mc2 (E rovná se m cé na druhou). Spousta fyziků aktivně přispívala ke vzniku relativistické dynamiky, o které se psala spousta článků a knih. Dlužno ale také dodat, že kromě těchto relativistických vztahů, které používáme dodnes, vznikalo také spoustu knih pojednávajících a vypočítávajících všemožné vlastnosti éteru, jako např. jeho pružnost, napětí, atd.. Tak z těchto článků a knih se dnes oprávněně nepoužívá vůbec nic.
Einstein přišel s tím, že přeformuloval celou v té době už vzniklou relativistickou dynamiku tak, že stála na dvoujednoduchých postulátech: postulátu, že světlo se pohybuje ve všech inerciálních soustavách toutéž rychlostí c, a na postulátu, že všechny fyzikální zákony mají stejnou formu ve všech inerciálních soustavách.
Říká se, že ďábel se skrývá v detailu, a v případě Einsteinových postulátů to platí vrchovatě. Stačí když si uvědomíme, že předpoklad, že fyzikální zákony mají stejnou formu ve všech inerciálních soustavách, byl formulován už nedlouho po Newtonovi. Mezi inerciálními soustavami se přecházelo Galileiho transformací (všimněme si mimochodem, že Einsteinovy postuláty nic explicitního o tom jaká transformace má bý užita, neříkají). Newtonova mechanika byla invariantní už dlouho. Problém vznikl až později s Maxwellovou dynamikou, která vůči Galileiho transformaci invariantní nebyla. Také to, že rychlost světla vycházela stejná ve všech inerciálních soustavách byl v té době dlouho známý experimentální fakt, takže v čem vlastně vězela Einsteinova genialita?
Vězela právě v tom detailu. Invariance vůči Galileiho transformaci byla dlouho známa, nicméně právě použitím této transformace vycházela rychlost světla různá v různých inerciálních soustavách. To, že rychlost světla vycházela stejná, bylo už také léta známo, ale tato skutečnost se chápala jakožto jakýsi zlomyslný vedlejší efekt kontrakcí. A celá do té doby velice složitě a pomalu se rodící relativistická dynamika byla až po uši ponořená v tisících stránkách pojednávajících o vlastnostech éteru. Éteru, který vlastně nikdo nemohl díky mnohem různým zlomyslnostem změřit, což ale nebránilo tomu, aby se o něm psaly stohy odborných pojednání.
Einsteinova genialita byla právě v tom, že ukázal, že celá ta složitá mašinerie okolo éteru je naprosto zbytečná. Kolikrát se mylně říká, že Einstein vyvrátil existenci éteru. Není to pravda, Einstein hypotézu éteru ve své teorii prostě nepoužil, byla nepotřebná. Vzal dva v té době už svým způsobem a s výhradami akceptovatelné fenomény - konstantní rychlost světla a invarianci fyzikálních zákonů - a ukázal, vezmou-li se tyto dva fenomény jako prostá afkta a bez výhrad (tj. ne jako jenom jakási náhodná shoda ve vhodně zvolených fiktivních souřadnicích, ale jakožto platné bez výhrad v reálných souřadnicích), tak lze získat všechny do té době velice pracně získané relativistické vztahy. To vše na pár desítkách stránkách papíru. A jako řešničku na dortu poslal do redakce dodatečné rozšíření jeho článku obsahující jeho rovnici E=mc2 - kterou nikdo před ním neodvodil.
Ukázalo se, že správná interpretace pouhých dvou jednoduchých postulátů měla neuvěřitelné konsekvence - na několika stránkách z nich byla odvozena Lorentzova transformace, bylo ukázáno, že právě Lorentzova, a nikoliv Galileiho transformace, udává ty skutečné souřadnice, které udávají vztah mezi inerciálními soustavami, získaly se všechny relativistické dynamické vztahy včetně vztahu pro závislost hmotnosti částice na jeho rychlosti (a odtud nemožnost urychlit podsvětelně se pohybující hmotné těleso dodáním konečné energie na rychlost světla), a také se získal světoznámý vztah E=mc2. Ten byl o pár desetiletí později tragicky využit v atomové bombě, později ale také k mírovému využití v jaderných reaktorech - ale to už je úplně jiný příběh.
Děkuji Pavlu Brožovi
Ota Beran,2011-10-06 11:09:41
za to, že mi pomohl po létech osvěžit dávno zapomenuté souvislosti vývoje fyziky. Je to moc pěkně a srozumitelně napsané i pro fyzikálního analfabeta jako jsem já.
Velmi zajimavé vysvětlení.
Karel Rabl,2011-10-05 17:50:06
Omlouvám se, jsem jen laik.
Ale tohle mě zajímá i když mám pořád pocit, že něco v té hmotě chybí, možná je to ta temná hmota.
Doplnění k vědecké hypotéze
Jan Turoň,2011-10-05 14:19:38
(doufám, že se toto zobrazí jako odpověď panu Wagnerovi na příspěvek "Co je to vědecká hypotéza" - jinak se omlouvám)
Souhlasím - ověřitelná nebo vyloučitelná předpověď je ale jen taková, která je jednoznačná a opřená o dříve dokázané věci. Nevím však, o co se opírá kupříkladu tvrzení "Keď však má fyzikálna veličina imaginárnu hodnotu nemôžeme ju v našom svete pozorovať.". Proč bychom nemohli? K odpovědi je třeba definovat pojem imaginární hmotnosti - modelem či efektem (fenoménem) - nestačí, že to pasuje do nějaké rovnice, fyzika přece není matematika. Ten efekt nemůže být nadsvětelná rychlost - to by byl důkaz kruhem. Navíc nabývám dojmu, že Petrovo tvrzení je také založeno na dvojznačnosti slova "reálné": v matematickém smyslu "neimaginární" a ve fyzikálním smyslu "skutečně existující" - to jsou přeci dva zcela odlišné pojmy.
Nesouhlasím, že nenalezení takových částic hypotézu vyvrací - je přeci možné, že jsme jen špatně hledali. (Samozřejmě, pokud se budou pohybovat jinak, je to vyvrácení mimo vší pochybnost.) Nezdá se mi postup, kde by se matematické rovnici dávala fyzikální interpretace: všechny příklady, co znám, dávají fyzikálnímu fenoménu matematickou interpretaci, nikdy ne naopak. Jako fyzik ale určitě takové příklady znáte - mohl byste mě na ně odkázat? Někde jsem četl zmínky (ale ne z odborného zdroje), které tvrdí, že sama STR je ten případ.
Hypotéza
Vladimír Wagner,2011-10-05 22:36:55
Vážený pane Turoni. Hypotéza nesmí odporovat věcem které se pozorovaly před tím, ale může to být klidně i něco úplně nového. Navíc "meta- relativita" (není to teorie vymyšlená Peterem Kluvánkem,takže možná by bylo dobré, kdybyste nahlédl do odkazovaného článku v Physics Today) není nic nového a jednoznačná a je opřená o dříve dokázané věci :-) Speciální teorie relativity je dříve dokázaná věc a tedy i Lorentzova transformace a daná rovnice popisující vztah mezi energií a rychlostí. V principu předkládaná tachyonová hypotéza pouze interpretuje řešení této rovnice, která jsou pro záporná čísla pod odmocninou.
Abych předešel nedorozumění, poznamenávám, že věc je složitější a "meta- relativita" nevystačí jen s tím.
Jestli je hypotéza správná a i tato řešení popisují reálný svět, musí prokázat experiment. Ten buď hypotézu potvrdí nebo vyloučí. Pokud se žádné částice, které by odpovídaly této hypotéze nenajdou, tak prostě zůstane pouze v oblasti hypotéz. Podobné to bylo i s předpovědí samotného neutrina Paulim. Dokud nebylo detekováno, tak byla hypotéza o jeho existenci pouze hypotézou. Příklad s předpovědí antičástic, které bylo hypotézou interpretující záporná řešení Dirackovy rovnice, jsem už zde referoval.
Hypoteza odpovedi :-)
Marek Fucila,2011-10-06 00:25:12
Pan Turon a dalsi, co sa Vam nedari odpovedat na zamyslane prispevky.
Podla mna je problem cisto v prihlaseni sa do diskusie. Ak nie ste na oslovi prihlaseni, tak kliknutim na "Odpovedět" sa Vam zobrazi vyzva na prihlasenie, a potom uz formlar na odpoved. Tento formular uz ale nedostane informaciu o tom, na ktory prispevok ste zamyslali reagovat, a preto sa Vasa odpoved zobrazi ako najnovsia, mimo zelaneho prispevku.
Vsetko co treba urobit je kliknut na prislusne "Odpovedět" aj druhy krat, po prihlaseni. Az potom pisat svoju odpoved.
V case pisania odpovede si mozete skontrolovat, ci sa po odoslani tato spravne zaradi jednoducho tak, ze nad formularom bude uvedene:
"Odpovědět na příspěvek
od: {autor} nadpis: {nadpis}". Ak je tam len "Přidat příspěvek do diskuse", treba opat kliknut na prislusne "Odpovědět".
Toto spravanie uz z principu nema nic spolocne s prehliadacmi, ale kedze ja som doteraz pisal len cez chrome, tuto hypotezu si prave overujem cez explorer.
Spravnym zaradenim tohto prispevku sa tato odpoved stane teoriou, ktoru este stale mozno vyvratit, ak to nepojde napriklad cez firex.:-) Inak si myslim, ze Vasa polemika o tom, ci je nejaka matematicka myslienka hypotezou vhodnou pre fyziku, pokial sa jej prinos (zatial) neopiera o pozorovanie nema v prince riesenie. Kazdy pouzivate inu definiciu fyzikalnej hyptezy. Obaja mate v obhajobe pravdu. Z casoveho hladiska vsetky nove teorie v pojmoch pana Wagnera sa stavaju hypotezami pana Turona. :-) Osobne sa mi vidi praktickejsie mat "naskok" aj za cenu toho, ze sa potom nejaky teoreticky fyzik mozno zbytocne zaobera niecim, co je mimo hmotnej reality.
PS: Este je mozno jedna moznost ako sa prispevok nedostane kam bol urceny, a sice ak ho clovek pise dlhsie ako je stanoveny limit servera pre odhlasenie kvoli necinnosti. Ak pisete prispevok dlho, server nevie ci ste este pri pocitaci. Po odoslani pravdepodobne bude vyzadovat opatovne prihlasenie a su 3 moznosti, co sa moze stat: 1. vsetko bude ok, 2. prispevok skonci nespravne zaradeny, 3.o svoj prispevok pridete.:-) Skusam odoslat...
usudzoval by som
Maroš Štulajter,2011-10-04 23:07:20
s toho že v tej dobe vedeli rozoznať iba elmg. žiarenie (svetlo)reprezentované fotónom ktorý je vlastne výsledkom pôsobenia elmg. síl. kritizoval to aj nikola tesla, tiež bol toho názoru že "c" by nemusela byť konečná rýchlosť lebo nezohľadňuje neutrálne častice ktoré sa nerozpadajú. neutrína sú inej povahy ako fotóny, hlavný rozdiel je v tom že nereagujú s el. nábojom a preto sú ťažko identifikovateľné.
s čoho usudzujem
Maroš Štulajter,2011-10-04 22:51:08
že by mala platiť iba pre častice el. nabité, presnejšie len pre leptony ktoré majú náboj lebo ostatné sa rozpadajú fakticky ostáva nám len elektrón, ten pri vyšších energiách vyžaruje synchrotrónne žiarenie, a tak sa bráni dosiahnúť "c". v dobe einsteina sa nevedelo o leptone ktorý by bol neutrálny. ja som hovoril o leptone nie o hadrone keďže vieme neutrálne hadróny sú poskladané s kvarkov ktoré majú el. náboj. pri neutrínach je to podstatne iné, tiež sú leptóny s podstatne menšou hmotnosťou a hlavne im chýba el. náboj čiže nemôžu interagovať s elmg. silami. interagujú len so slabimi silami vnútri hadrónu, tzn. že ich identifikácia je veľmi ťažká. preto ich einstein nemohol zapracovať do jeho str. nakoniec aj samotné odvodenie "c" je odvodené od el. hodnôt vákua. pri neutrínach je zaujímavá aj antičastica ktorá tiež prechádza hmotou len produkt jej interakcie je opačný.
Re:
Vít Výmola,2011-10-05 20:26:15
Ale Einstein nemusel nijak do STR zapracovávat neutrální leptony, i kdyby už v té době byly známy. Teorie relativity nemá nic společného s elmag interakcemi, nemá nic společného s podstatou částic. Pracuje s hmotou jako takovou. Omezení na rychlosti menší než c opět nijak nesouvisí s interakcemi, vychází z něčeho úplně jiného.
toto není hypotéza
Jan Turoň,2011-10-04 16:14:26
Pane Wagnere, nesouhlasím, že se jedná o hypotézu. Mohu kupříkladu tvrdit, že částice mohou letět rychleji než světlo díky kouzlu. Není to hypotéza, dokud nevysvětlím, co mám tím kouzlem na mysli. Stejnětak Petr nevysvětluje, co je to imaginární hmotnost. Každá hypotéza by proto měla být ucelená, souhlasíte?
Fyzika se liší od matematiky tím, že operuje s reálnými fenomény. Hmotnost lze definovat třeba fenoménem gravitačního působení na okolí (A) nebo tlakem na podložku váhy (B). Definice B tvrdí, že vodík má zápornou hmotnost. Mohu to prakticky využít: protože F=m*g, mohu vypočítat antigravitační sílu vodíkového balónu. Z definice A dostanu vždy kladnou hmotnost (vodíkové hvězdy planety vždy přitahují) a pro balónové létání bych musel vymyslet jiný teoretický model (třeba Archimedův zákon). Oba modely by ale popisovaly totéž: fenomén reálného světa.
Petr se pohybuje v říši matematiky, která se neopírá o fenomény, jinými slovy nemá s realitou nic společného, jinými slovy je z říše pohádek.
Jako laika mě (především z gnoseologického hlediska) pozadí výzkumu u Diracovy rovnice a záporné energie velmi zajímá. Nepsal jste o tom někde ve svých popularizačních článcích?
-
Z Z,2011-10-04 17:05:02
Petr nevysvětluje, co je to imaginární hmotnost.
To nemusí, išlo o imaginárnu kľudovú hmotnosť a hypotetický tachyón by v kľude, podľa tej hypotézy, nikdy byť nemohol. Rovnako je hypotetická nulová kľudová hmotnosť fotónu - tú tiež nikto neodmerá. Podľa tej hypotézy by bola hmotnosť (pohybujúceho sa) tachyónu reálna kladná (E/c²).
Co je vědecká hypotéza
Vladimír Wagner,2011-10-04 21:09:10
Vážený pane Turoni, jak definujete pojem hypotéza. Ovšem vědecká hypotéza je vědecký předpoklad, jehož platnost teprve potřebuje ověřit. Nutnou podmínkou u ní je, že musí hypotéza dávat předpovědi, které jsou ověřitelné nebo vyloučitelné.
A hypotéza o meta-relativity je opravdu typycká hypotéza. Předpovídá existenci částic, které se pohybují rychlostí větší než je rychlost světla ve vakuu, a navíc dokonce předpovídá, jak bude vypadat pohybové rovnice pro takové částice. Hypotézu lze potvrdit tak, že se najdou částice rychlejší než světlo a budou se pohybovat podle uváděných rovnic. Vyvrátit tak, že se žádné částice rychlejší než světlo nenajdou nebo že se budou pohypovat jinak.
Hypotéza pochopitelně (a týká se to i potvrzené teorie) nemusí vysvětlit vše. V hypotéze "meta-relativity se vysvětluje, že imaginární hmotnost v dané rovnici je spojená s nadsvětelnými částicemi a reálná s podsvětelnými.
Teorie "meta-relativity" předpovídá "reálné" fenomény (nevíme jestli existují) a dává matematickým rovnicím fyzikální interpretaci.
O Dirackově rovnici a historii předpovědi a objevu antičástic přednáším studentům, psát jsem o tom speciálně nepsal, ale možná že bych v budoucnu nějaký takový historický článek mohl napsat
imaginarne cisla
peter hrasko,2011-10-04 15:15:54
Mna by aj tak zaujimal nejaky laicky pochopitelny geometricky model popisujuci princip imaginarnych cisel.
Uz davnejsie som cital penroseho road to reality a on sa tam vyjadril ze komplexne cisla su nieco comu nikto nerozumie. Je to naozaj pravda?
Peter Mak,2011-10-04 19:31:23
Možno celý problém zvulgarizujem ale podľa mňa ide o niečo podobné ako v nasledujúcom prípade:
Bača ma 10 oviec. Susedovi ich predá 11. Nie je to divné lebo do zmluvy napíšu, že posledných 5 dodá až na jar.
Žiadna záporná ovca neexistuje ale na dlhy sme si privykli. Záporné čísla nás nefascinujú tak ako imaginárne. Pritom sa jedná rovnako len o užitočnú myšlienkovú konštrukciu.
Byla to nadsázka
Pavel Brož,2011-10-04 19:36:59
Komplexní čísla využívají matematici, fyzici, inženýři atd. už několik století, vyučují se i na středních školách, tvoří samozřejmou náplň studia matematiky na vysokých školách pro mnoho různých oborů, takže by bylo nereálné očekávat, že jim nikdo nerozumí.
Na druhou stranu je otázka, kdo to říká. Asi každý z nás si myslí, že ví, co jsou to přirozená čísla. Ale kdyby nějaký matematik, specialista na teorii čísel, řekl analogicky jako Penrose, že přirozeným číslům nikdo nerozumí, měl by svým způsobem samozřejmě pravdu. Existuje dodnes obrovské množství nezodpovězených vlastností přirozených čísel (např. jen prvočísel), a jejich vztahu k jiným důležitým oblastem matematiky. Např. důkaz velké Fermatovy věty, která je výrokem pouze o přirozených číslech, trval přes dvě století a zabral přes dvě stě stran velice hutné a těžké matematiky.
ako by asi vyzerala einsteinová teoria relativity
Maroš Štulajter,2011-10-04 12:37:00
keby poznal neutrína. v tej dobe o nich netušil. neutrína vznikajú pri beta rozpade a pôsobia iba na slabé interakcie, nemajú el. náboj tzn. nevieme ich priamo identifikovať. tu je asi kameň úrazu pri definícii t.r. einsteinom. einsteinová teória podľa posledných zistení by mohla platiť len pre častice ktoré majú el. náboj. po takej dlhej dobe keď poznáme hmotu oveľa lepšie tak by aj t. r. mohla byť doplnená. z grafou pre čas extrakcie neutrín nie je mi celkom dobre známe odkiaľ sa odoberá začiatok impulzu, či z dopadu protónov na terčík alebo detekciou neutrín
Ještě jeden dodatek k této tachyonové teorii
Vladimír Wagner,2011-10-04 08:23:28
Obrázek 1, který ukazuje Peter Kluvánek, je trochu zavádějíci (je však správný). Má pravou a levou stranu symetrickou. To je ovšem dáno čístě tím, kde Peter na pravé straně závislost uřízl. Na lévé straně je omezení nulou, ale na pravé se může táhnout do nekonečna. To vede k tomu, že pro velmi vysoké rychlosti přesahující dvojnásobek rychlosti světla můžeme při daším ubírání energie dostat energie menší než energie klidová (alespoň vzpomínaná závislost to dovoluje) až téměř k nule. I to je jeden z řady problémů, které by se musely v této teorii řešit.
Dagmar Gregorova,2011-10-04 09:32:41
:)
Myslím, že nemá velký smysl dohledávat nepřesnosti a neúplnosti na článku Petra Kluvánka. Je to rozumně napsaný článek o tom, že teorie umožňuje dostatečně odvážným fyzikům uvažovat i o zatím hypotetických částicích, rychlejších než světlo - a také se zabývá oblasti okolo této magické limity. Nejde napsat vše v relativně krátkém popularizačním článku, kde autor musí uvažovat na jaké úrovni je nutné začít vysvětlovat odborníkovi pojmy jasné a samozřejmé. Myslím si, že dobrým, promyšleným způsobem přibližuje lidem, kteří jsou sice odborníci, ale v jiném oboru, než fyzikálním (kde jsou laiky) "vo co go", tedy aby alespoň měli "tušáka", že existují tachyony a o co jde. Takovým lidem - a těch je mezi čtenáři nejvíce - dodatky již máloco řeknou a diskuze pak oslovuje hlavně autora a několik nadšenců. Mně samotné tento článek hodně napověděl.
Jistě není lehké psát o něčem, co je čistě teoretické, manipuluje "to" s imaginárními hodnotami a je děsně kontraintuitivní, co se běžného života týče. Vždyť pro nás laiky je otázkou, jako vůbec registrovat tachyon, letící rychleji, jako případná informace o něm. Bezpochyby by to chtělo "upgrade" i v souvislosti s výsledky OPERY. Ale napsané srozumitelně i pro "laiky". Takže to, fyzikové, berte jako výzvu... :) :) :)
Ta upřesnění jsou ale naprosto legitimní
Pavel Brož,2011-10-04 11:40:10
Myslím, že je naprosto legitimní, přinést v diskuzi upřesňující informace. Od toho ty diskuze jsou, aby bylo možno dovysvětlit, upřesnit či přímo opravit dílčí tvrzení v článku. I když ten článek je dobrý, tak bohužel jeho uvedení v kontextu s posledními neutrinovými experimenty může hodně mást.
Mimochodem, úplně stejně může mást ta příšerná reklama na tu knihu Energie tachyonu, uvedená pod tímto článkem. Nemálo čtenářů si může myslet, že je to nějaká odborná či popularizační kniha o částicové fyzice. Kdepak, je to naprostý blábol. Už jsem se o tom bavil s Josefem, bohužel ty reklamy tam cpe příslušný inzertní systém a není možné do toho jednoduše šáhnout a vysmahnout to pryč.
Článek Petera Kluvánka není špatný, ale v kontextu posledních objevů může mnohé čtenáře poněkud zmást. Proto naprosto souhlasím s tím, že dílčí informace byli Vladimírem Wagnerem doupřesněny.
Smysl diskuze pod článkem
Vladimír Wagner,2011-10-04 22:37:31
Je několik oblastí, kde může být diskuze přínosem. Je možné doplnit informace v článku. Upřesnit něco, co autor za příliš důležité nepovažuje, ale jiní mohou. Druhou oblastí je možnost dotazu do fóra či k autorovi o problému, který je s tématem spojen. Je jasné, že se lidé budou různit v pohledu, jak důležité jsou upřesnění, doplnění či dotazy. Nevidím však důvod, proč by se na to měla dělat "nějaká autocenzura" a propouštět jen to, co by mohli považovat za důležité všichni (jak to poznat?). Diskuzi nemusí číst, každý, takže nemusí vadit i rozbor detailů.
Tím se dostávám k třetí oblasti, kterou v diskuzi považuji za pozitivní. A to je možnost autora se poučit, kde by se příště mohl vyhnout nepřesnostem či ještě srozumitelněji předložit své myšlenky čtenáři. Ve vlastním článku člověk často přehlédne to, co druhý jasně uvidí. Pro mě je pak pro další psaní diskuze pod články velkým přínosem. Proto prosím, pod mými články určitě pište všechny poznámky, třeba i k "drobným" nepřesnostem a místům, které mohou být zavádějící.
Pokud je diskusní příspěvek slušný, bez invektiv a k věci, tak je vždy přínosem.
Peter popisuje pouze jednu tachyonovou teorii
Vladimír Wagner,2011-10-03 22:31:33
Možná, že došlo k nedorozumění. Nemám nic proti článku. Považoval jsem a považuji za nutné pouze vysvětlit několik hodně podstatnou věc, která může být pro fyziky neznalého čtenáře dost zavádějící. Článek redakce uveřejnila v souvislosti s posledním experimentem OPERA a jeho výsledkem. Takže neznalý čtenář může nabýt nesprávného dojmu, že by třeba tachyony popsané v článku mohly výsledek tohoto experimentu vysvětlit a popsat. To ovšem nemohou. To, co Peter Kluvánek osvětluje, nejsou tachyony a tachyonové teorie obecně, ale pouze teorie "meta-relativity", která předpokládá, že pohyb tachyonů (jen v této teorii, tedy jednoho vybraného druhu ne obecně) lze popsat stejnou rovnící jako pohyb "podsvětelných" částic. Jen se zavede popis jejich hmotnosti pomocí hmotnosti imaginární. V tomto případě však je křivka závislosti energie na rychlosti pouze zrcadlově převrácená a přibližuje se shora k rychlosti světla úplně stejným způsobem jako závislost podsvětelných částic zdola. A to u známé limity na velikost hmotnosti neutrina vede k tomu, že se u 30 GeV neutrin (v podstatě u všech neutrin s takovou energií, abychom je dokázali detekovat) jejich rychlost od rychlosti světla bude lišit o mnoho řádů méně než je výsledek OPERY. Proto nemůže být právě tato tachyonová teorie, kterou popisuje Peter, uplatněna pro tento případ. A musí se pro případné vysvětlení pozorování OPERY použít úplně jiná. Moje poznámka neměla být kritikou Petera, redakce či kohokoliv jiného, pouze chtěla osvětlit podle mě důležitou okolnost, kterou ani článek a ani redakce nevysvětlily.
Omluva
Vladimír Wagner,2011-10-03 22:38:15
Omlouvám se za špatné přiřazení, mělo jít o odpověď na poznámku Josefa Pazdery.
Souhlasím
Pavel Brož,2011-10-03 22:49:55
Myslím si, že je velice dobře, že toto bylo řečeno, protože hodně čtenářů by si opravdu chybně spojilo tento pět let starý článek s výsledky Opery (přiznám se, že i já jsem se po prvním rychlém čtení nejprve chytal za hlavu, teprve reakce Josefa mě přiměla přečíst si znovu tiráž článku, kterou jsem na první čtení přehlédl).
Ačkoliv se opravdu o tachyonech spekulovalo v minulosti už vícekrát, tak pokud jsou současné výsledky z CERN správně, tak to znamená úplně odlišný vztah pro závislost energie na rychlosti, než může poskytnout standardní relativistický vztah, bez ohledu na to, jakým způsobem se rozhodneme interpretovat (či ignorovat) imaginární hodnoty z tohoto vztahu vyplývající.
Gf Fs,2011-10-04 00:25:16
Argument hmotnosti neutrina je velice dobry, ovsem klasicky argument proti tehle konkretni tachyonove teorii v pripade neutrin je Cerenkovovo zareni. Neutrino letici rychleji nez svetlo ve vakuu bude emitovat 1. foton, 2. par neutrino-antineutrino, 3. par elektron-positron. Nic takoveho zadny experiment nikdy nepozoroval. V pripade experimentu OPERA je tenhle argument dotazeny do konce treba tady:
http://arxiv.org/abs/1109.6562v1
Nemůže jít o Čerenkovovo záření
Vladimír Wagner,2011-10-04 08:08:28
V tomto případě nemůže jít o Čerenkovovo záření. Čerenkovovo záření mohou vyzařovat pouze nabité částice. Kdyby neutrino vyzařovalo Čerenkovovo záření, tak by je pochopitelně vyzařovalo i při téměř každém pohybu libovolným materiálem (vždy je rychlejší než světlo v tomto materiálu). Proto je v tom odkazovaném článku řečeno "něco jako Čerenkovovo záření". I tato formulace je podle mého názoru velice nevhodná a zavádějící, a navíc zbytečná. V článku se pak v jiných místech referované záření označuje jako brzdné. I v tomto případě je toto označení zavádějící. Brzdné záření vzniká v připadě, když nabitá částice (v tomto případě nemusí jít o elektrický náboj ale také třeba náboj silné interakce) je jinými náboji či poli ovlivněna a působí na ni zrychlení (zpomalení). Pak vyzařuje částice příslušného pole, tedy buď fotony nebo gluony. Pokud správně chápu článek, tak by se podle autorů mělo jednat o interakci elektroslabého pole ve vakuu se "slabým" nábojem neutrina a vyzařování neutrálních polních částic elektroslabé interakce, tedy fotonu nebo Z bosonu. Z boson se pak mění na pár neutrino a antineutrinu nebo elektron a pozitron. Ale řekl bych, že to není proces, který by musel probíhat na základě standardního modelu. Jeho existence či neexistence je modelově závislá. Takže asi nemůže být důkazem nemožnosti jevu OPERY. Ale nejsem na takové teorie expert. V žádném případě však nejde o Čerenkovovo záření a už vůbec ne o "klasický" argument proti meta relativistické tachyonové povaze neutrina. Buď by popsané záření existovalo a pak by byly vyloučeny všechny tachyonové teorie, nebo ne a pak nevyloučí žádnou.
preco trocharit
Pavel Ondrejovic,2011-10-03 22:16:20
Pri vhodne zavedenej komplexnej rychlosti a komplexnej kludovej hmotnosti, dostaneme realnu energiu tiez ;)
Pripadne staci sa naucit stuchat do gulecnikovej gule v imaginarnej ose a urychlime ju na rychlost 2c obidenim problemovej rychlosti "c" vrchom :)
slabé odvozování
Jan Turoň,2011-10-03 21:29:54
Jaké opodstatnění má dogma "v reálnom svete sú prítomné len reálne čísla"? Imaginární čísla jsou konstrukt, který řeší problémy reálného světa (původně kubickou rovnici). Obecně vytváříme konstrukty (např. sčítání, desítková soustava), abychom uměli popsat reálný svět. Je ale neprůkazné dělat to naopak - z konstruktů zkoumat reálný svět: z toho může vyplynout nejvýš hypotéza - aby se stala teorií, musíme na ní stejně aplikovat ten první přístup. Můžeme se opájet představami typu "obdélník s imaginární hranou má záporný obsah" - to ale nepopisuje žádný reálný problém, proto je toto tvrzení bezobsažné. Hypotézy lze tvořit jednodušeji: prostým plácáním do větru. Tedy pro termín "imaginární hmotnost" je nutné mít nějaké opodstatnění (například popsat hmotnost jako interakci s higgsovým bosonem pomocí rovnice, která by dávala imaginární řešení). Bez tohoto pozadí tedy článek pouze tvoří bezobsažné problémy místo aby REÁLNÉ problémy ŘEŠIL. Proto si myslím, že článek není popularizační, ale zavádějící: výsledkem může být pouze diletantská úvaha "ono se mi to nesmyslno vykrátí, takže to dává smysl". Nejprve je nutno vysvětlit, jaký REÁLNÝ fenomén zavádí pojmy "imaginární energie" a "imaginární klidová hmotnost" - pak teprve můžeme tyto fenomény zkoumat a zjišťovat, jestli i na ně platí STR.
-
Z Z,2011-10-03 21:54:31
Tedy pro termín "imaginární hmotnost" je nutné mít nějaké opodstatnění (například popsat hmotnost jako interakci s higgsovým bosonem pomocí rovnice, která by dávala imaginární řešení)
No veď presne to je v článku spravené. Riešenie v množine reálnych čísel rovnice (1) pre v a E:
Pre v0
Pre v=c platí m0=0
Pre v>c platí že m0 je rýdzoimaginárne
Ak by ten hypotetický tachyón exitoval, tak by bol pojem jeho kľudovej hmotnosti podobne nezmyselný ako pojem kľudovej hmotnosti fotónu - napriek tomu fotón existuje.
Nutnost fyzikální interpretace
Vladimír Wagner,2011-10-03 22:52:17
Pravdou je, že zdánlivě "nesmyslné" řešení fyzikální rovnice může dostat smysl jedině díky jeho nové fyzikální interpretaci. To je v daném případě předpověď tachyonu, který se přibližuje rychlosti světla z druhé strany. Jde o hypotézu. Teorií by se stala pouze, pokud by takové tachyony, které by šly touto rovnicí popsat, byly pozorovány.
Podobné nalezení nové fyzikální interpretace zdánlivě nesmyslného řešení (záporná energie jako řešení Dirackovy rovnice) vedlo k předpovědi antičástic a jejich pozdější objev změnil hypotézu na velice plodnou teorii.
doplnění, co je to vědecká hypotéza
Jan Turoň,2011-10-05 14:16:11
Souhlasím - ověřitelná nebo vyloučitelná předpověď je ale jen taková, která je jednoznačná a opřená o dříve dokázané věci. Nevím však, o co se opírá kupříkladu tvrzení "Keď však má fyzikálna veličina imaginárnu hodnotu nemôžeme ju v našom svete pozorovať.". Proč bychom nemohli? K odpovědi je třeba definovat pojem imaginární hmotnosti - modelem či efektem (fenoménem) - nestačí, že to pasuje do nějaké rovnice, fyzika přece není matematika. Ten efekt nemůže být nadsvětelná rychlost - to by byl důkaz kruhem. Navíc nabývám dojmu, že Petrovo tvrzení je také založeno na dvojznačnosti slova "reálné": v matematickém smyslu "neimaginární" a ve fyzikálním smyslu "skutečně existující" - to jsou přeci dva zcela odlišné pojmy.
Nesouhlasím, že nenalezení takových částic hypotézu vyvrací - je přeci možné, že jsme jen špatně hledali. (Samozřejmě, pokud se budou pohybovat jinak, je to vyvrácení mimo vší pochybnost.) Nezdá se mi postup, kde by se matematické rovnici dávala fyzikální interpretace: všechny příklady, co znám, dávají fyzikálnímu fenoménu matematickou interpretaci, nikdy ne naopak. Jako fyzik ale určitě takové příklady znáte - mohl byste mě na ně odkázat? Někde jsem četl zmínky (ale ne z odborného zdroje), které tvrdí, že sama STR je ten případ.
-
Z Z,2011-10-03 17:01:20
Keď už sa čaruje s komplexnými číslami, tak majú možno tachyóny reálnu hmotnosť, možno aj zápornú, a imaginárnu energiu. Alebo sú skoro celkom imaginárne, so slabými reálnymi zložkami v niektorých fyzikálnych veličinách.:-)
Takové tachyony výsledek OPERY nevysvětlí
Vladimír Wagner,2011-10-03 16:03:29
Je však dobré říci, že tachyony popisované Petrem Kluvánkem nemohou výsledek experimentu OPERA v žádném případě vysvětlit. Popsaná teorie tachyonů vychází z toho, že i svět tachyonů je popsán uvedeným vztahem speciální teorie relativity mezi energií a rychlostí. Jen hmotnost je imaginární. Ovšem velikost hmotnosti a tedy i kvadrátu hmotnosti (ten by byl záporný) pro neutrina by musel být stejně malý jako pro neutrina netachyonová. Tedy třeba z rozpadu tritia by vycházelo, že velikost hmotnosti (imaginární) by byla menší než 2 eV. Připomínam, že rozdíly mezi hmotnostmi neutrin jsou menší než desetina eV. A při energii 30 GeV by tak rozdíl mezi rychlostmi neutrina a světla vypočtený z uvedené rovníce o velký počet řádů menší než pozoruje OPERA.
Jen pro zajímavost, pravě záporná hodnota kvadrátu hmotnosti byla důvodem, proč polský fyzika Jakub Rembielinsky uvažoval s možností vysvětlit přebytek elektronů s maximální energií v rozpadu tritia pozorovaný v Hedelberku i Troicku tím, že jsou neutrina tachyony (viz http://hp.ujf.cas.cz/~wagner/popclan/neutrina/neutrina.html).
Pro vysvětlení experimentu OPERA by byla potřeba úplně nová fyzika, ve které by se pohyb tachyonů v žádném případě nedal popsat speciální teorií relativity, Ani v případě interpretace imaginárních výsledků pro dané imaginární hodnoty odmocniny a hmotnosti
článek není reakcí na výsledky exp. OPERA!
Josef Pazdera,2011-10-03 20:03:44
Článek Petra Kluvánka si vyžádala redakce protože jde o zajímavé a laikům srozumitelné vysvětlení co jsou tachyony. Jak je v článku dvakrát zmíněno, byl napsán v roce 2006 a tedy není reakcí ani možným vysvětlením nových výsledků experimentu OPERA.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce



