Před pár dny jsem na Oslovi psal o studiu systémů se zápornou teplotou. Pod článkem se rozvířila bouřlivá diskuze, která odhaluje, že intuitivní představy o některých termodynamických pojmech vedou často k fyzikálně nesprávnému pochopení. Proto je vhodné některé vlastnosti systémů se zápornou teplotou detailněji objasnit. Zkusme se také podívat na to, jak konkrétně se experimentálně takové systémy připravují a jak se záporná teplota u nich měří.

Co je „záporná teplota“?
Nejdříve si krátce připomeňme, co vlastně pojem záporná teplota znamená. Detailněji se tomu věnuje předchozí článek. V něm jsme si připomněli, že teplotu můžeme definovat různými způsoby. Můžeme vycházet z termodynamických veličin, mezi něž patří i entropie. Její statistická interpretace nabízí i jednu z možností jak teplotu definovat a určit. Další cesta ke stanovení teploty vede například přes kinetickou teorii plynů. Existují i další možnosti. V běžných podmínkách si tyto různé interpretace a definice odpovídají a umožňují vzájemnou kalibraci teplot měřených různými způsoby. V hraničních oblastech však mohou některé interpretace selhávat a jiné vést k zobecněním pojmu teploty pro popis nových specifických termodynamických systémů. V námi zkoumaném případě jsme se zaměřili na využití entropie (tedy míry neuspořádanosti) systému. Teplotu lze určit ze změny tepla (energie) odpovídající jednotkové změně entropie. V normálních podmínkách entropie při dodávání energie (tepla) roste a teplota je kladná. Pro velmi nízké teploty se však kromě energie chaotického pohybu atomů a molekul začíná projevovat energie spojená s jinými stupni volnosti. A stále více se projevují kvantové vlastnosti. Různé stupně volnosti mohou mezi sebou intenzivně interagovat (výměna energie mezi nimi je velmi rychlá a silná) nebo mohou být do značné míry oddělené (výměna energie mezi nimi je malá a pomalá).
Existují pak speciální kvantové systémy, u kterých může entropie s dodáváním energie klesat a tedy - i když do značné míry „formálně“ - dostáváme záporné teploty. Tyto systémy musí splňovat několik podmínek. Hlavně musí existovat jen omezený počet stavů a jejich energie musí mít diskrétní a omezené hodnoty. Dále musí být omezen přenos energie k jiným stupňům volnosti.
Pojďme se podívat, jak vypadá situace v zjednodušeném případě, když máme pouze dvě diskrétní úrovně energie. Pokud bychom měli všechny částice „zamrzlé“ v energeticky nižším stavu, teplota i entropie by byly nulové (systém je plně uspořádaný a existuje jediný mikrostav, kterým můžeme dostat daný makroskopický stav). Pokud budeme dodávat systému energii, poroste entropie i teplota. V určitém okamžiku, když máme přesně polovinu částic v nižším a polovinu ve vyšším energetickém stavu, dosáhne entropie maximální hodnoty a s dalším dodáváním energie začne klesat. V tom případě teplotu definovanou pomocí entropie dostáváme „formálně“ jako zápornou. S dalším dodáváním energie klesá jak entropie, tak se zmenšuje i velikost záporné teploty. Když se nám podaří dodat tolik energie, že zamrazíme všechny částice do spinové orientace s vyšší energetickou hodnotou, opět dostaneme stav s nulovou entropií. Také teplota bude nulová, tentokrát však dosažená ze „záporné“ strany (nárůstem tepla jsme dospěli k nule). I v tomto případě se však můžeme k hraniční hodnotě jen limitně přibližovat. Je třeba zdůraznit, že systém se zápornou teplotou je teplejší než systém s kladnou a dochází k přetoku energie od systému se zápornou teplotou k tomu s teplotou kladnou.

Ještě bych rád znovu zdůraznil nedosažitelnost absolutní nuly jak ze směru kladných teplot, tak ze směru teplot záporných. A nedochází tak ani u záporné teploty k porušení třetího termodynamického zákona. Ostatně jsou pro ni splněny i další termodynamické zákonitosti. Pro lepší názornost nedosažitelnosti teploty absolutní nuly a spojitého přechodu přes nekonečno je možné systém se zápornou teplotou charakterizovat ne teplotou, ale její převrácenou hodnotou. Pak máme plus nekonečno a mínus nekonečno v místech nedosažitelné absolutní nuly. A místo přechodu přes nekonečno, přecházíme přes nulu. Pro klasické teploty ovšem dostaneme nulu a tedy pro laika zdání dosažitelnosti na straně v tomto případě nedosažitelné nekonečné teploty. Pro klasickou teplotu můžeme použít raději logaritmus teploty, jak třeba zmiňuje i Max von Laue ve svých Dějinách fyziky. To pak máme pro absolutní nulu záporné nekonečno a pro nekonečnou teplotu nám zůstává plus nekonečno. Tento popis však nelze použít v případě kvantového systému se zápornými teplotami. Běžná laické zkušenosti se ale vymyká převrácená hodnota teploty či dokonce její logaritmus a tak nám tyto změny popisu při popularizaci moc nepomohou.
Zastavme se ještě u podmínek, které umožňují nastolit termodynamickou rovnováhu systému, při které dostaneme konstantní (či jen relativně pomalu se měnící) a dobře definované hodnoty termodynamických stavových veličin (teploty, entropie, …). Ta může nastat jedině v případě, že výměna energie mezi systémem a okolím je mnohem pomalejší než výměna energie uvnitř systému, která umožňuje vyrovnání hodnot zmíněných stavových veličin uvnitř něho. „Klasickým“ příkladem takového systému je šálek s čajem právě zalitým horkou vodou. V hrnečku se teplota ustálí mnohem rychleji, než probíhá její vyrovnávání s okolím. Horký čaj je tak při chladnutí v termodynamické rovnováze a jeho teplota je tak dobře definována.
Spinové systémy, spinová teplota
V minulém povídání jsem se zmínil o komplexnějších kvantových systémech, které se zatím objevily pouze v teoretickém návrhu. Nyní bych se věnoval pouze jednomu typu jednodušších kvantových systémů, u kterých lze docílit záporných teplot. Jde o systémy spinové. Jejich experimentální realizace a studium probíhá v laboratořích už od padesátých let. Spin (vnitřní úhlový moment hybnosti) částic nebo jader je spojen i s existencí magnetického momentu. Částice nebo jádro se tak v magnetickém poli chová jako malá magnetka. Energii pak určuje její orientace vůči vnějšímu magnetickému poli. Zaměřme se na nejjednodušší situaci, kdy je spin částice nebo jádra 1/2. V tomto případě mohou být jen dvě možnosti orientace spinu a hodnoty energie. Jde o případ, který nastává například u jader stříbra a rhodia, proto se i často používají k experimentům. Tato jádra jsou součástí například krystalu, který lze umístit do magnetického pole. Pro to, abychom mohli dosáhnout záporné spinové teploty a zkoumat ji, musí být přenos energie mezi spinovými stupni volnosti příslušných jader a jinými stupni volnosti krystalové mříže omezený a pomalý. To umožňuje dosáhnout spinovou teplotu dlouhodobě odlišnou od teploty krystalové mříže. Podmínkou je mnohem rychlejší přenos energie spojené s orientací jader v magnetickém poli mezi těmito jádry než jiná výměna energie s krystalovou mříží či okolím.
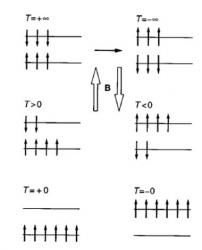
Situace, že dvě prolínající se složky mohou mít dvě různé, dobře definované teploty, není zase tak neobvyklá. Opět však musí platit, že přenos energie mezi částicemi určité složky je mnohem rychlejší než mezi částicemi různých složek. Jde třeba o případ plazmatu, v němž mohou mít elektrony a ionty různé teploty z důvodu velmi velký rozdílů jejich hmotností. Ještě exotičtější případ je vesmírné reliktní záření, jež vyplňuje homogenně celý kosmický prostor. Jeho teplota zhruba 2,73 K je nezávislá na ostatních složkách tvořících vesmír. Je to dáno tím, že neexistují procesy, ve kterých by si fotony reliktního záření mohly vyměňovat energii s ostatní hmotou.
Představme si, že chceme zkoumat, jak extrémně horký systém postupně chladne a jak se při tom mění jeho teplota. Chci ukázat, že není tak velký rozdíl, když například s obyčejnou vodou experimentují studenti v laboratoři na gymnáziu nebo se spinovým kvantovým systémem zabývají vědci v moderní fyzikální laboratoři. Studenti vezmou varnou konvici a uvedou vodu do varu. Pak ji přelijí do hrnce, počkají, až se teplota v hrnci vyrovná v celém objemu a změří teploměrem poprvé teplotu. Pak budou v pravidelných intervalech měření opakovat a vynášet závislost teploty na čase, až dokud se teplota neustálí, tedy nevyrovná s okolím. Zjistí, jak probíhá ochlazování vody v daném hrnci na pokojovou teplotu.
Popišme si nyní měření teplotních změn kvantového spinového systému.
Jak získat zápornou teplotu?
Místo varné konvice musíme použít trochu jiný trik. Vhodný krystal (materiál) umístíme do silného homogenního stejnosměrného magnetického pole. Spiny jader (jaderné „magnetky“) se postupně orientují. Velká většině z nich se podaří natočit se vzhledem na směr vnějšího působícího pole tak, že se nachází v nejnižším energetickém stavu. Existují pak způsoby, jak i z takového systému odebrat energii, aby opravdu co největší procento spinů bylo orientováno energeticky nejvýhodnějším směrem. Pak krystal ve stejné poloze přesuneme do opačně orientovaného magnetického pole. Usměrnění spinů většiny teď odpovídá stavu s největší možnou energií. Tím se systém velmi chladný stal systémem velmi horkým. Jak jsme si řekli, výměna energie mezi spinovými stavy probíhá velmi rychle. Naopak, ve srovnání s ní únik energie do jiných stupňů volnosti, pryč ze spinového systému, probíhá velmi pomalu – relaxační doba je relativně velmi dlouhá.
Stejně jako po přelití horké vody do hrnce i u spinového systému dostaneme rychle termodynamickou rovnováhu. Po změně magnetického pole se ustálí za velmi krátký čas. Systém tak má dobře definovanou spinovou teplotu. Protože většina spinů se nachází ve stavu s větší energií, při překlápění části z nich do stavu s nižší energií (třeba právě unikem energie do jiných stupňů volnosti) dochází k úbytku energie systému, ale k nárůstu entropie. Teplota je tedy záporná. Pokud pole vypneme, tak v případě kladné i záporné teploty se začne restaurovat náhodné rozložení orientace spinů, tedy entropie se zvyšuje, až se systém ustálí ve stavu s její maximální hodnotou. Tedy v obou případech v souladu s druhým termodynamickým zákonem. A právě takové experimenty jsou prováděny už od roku 1951, kdy zmíněný systém poprvé připravili E. M. Purcell a R. V. Pound. Při experimentech je důležité najít systém, u něhož je relaxační doba, která uplyne, než se spinová orientace ztratí, co nejdelší. Tedy stejně jako u horké vody i chladnutí kvantového spinového systému bude pomalé.
Jak zápornou teplotu měřit?
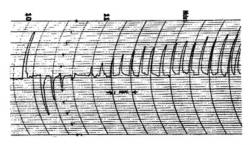
K tomu lze využít metodu jaderné magnetické rezonance. Na systém začneme působit proměnným elektromagnetickým polem se správnou frekvencí, která dokáže měnit orientaci příslušných spinů (magnetek). Můžeme si to představit i tak, že fotony odpovídajícího elektromagnetického záření musí mít takovou energii, která je rozdílem mezi energií vyššího a nižšího stavu. Přesná hodnota frekvence je závislá na intenzitě stálého magnetického pole, ale v každém případě spadá do oblasti rádiových vln. Krátký puls takového proměnného elektromagnetického pole způsobí v systému změnu entropie a tedy i energie. Systém má tendenci dosáhnout stav s maximální hodnotou entropie (tedy s vyrovnaným množstvím jader orientovaných v různých směrech). V případě záporných teplot energie pole naroste, spiny do něj část energie uvolní, a dostaneme spektrum emisní. V případě kladných teplot je naopak energie z proměnného elektromagnetického pole odebrána a absorbována spiny. Dostaneme tak absorpční spektrum. Tak trochu je to možné přiblížit pomocí emisních a absorpčních čar v klasickém spektru třeba Slunce nebo hvězd. Z formy absorpčního či emisního píku pak lze určit teplotu systému.
Jak už bylo zmíněno, první takový systém připravili a zkoumali už v roce 1951 E. M. Purcell a R. V. Pound. Použili krystal fluoridu lithného, který má velice dlouhý relaxační čas, jak v intenzivním magnetickém poli tak bez něj. Systém má velmi výhodné vlastnosti. Procesy interakce mezi spiny, které nastavují termodynamickou rovnováhu ve spinovém systému, jsou velmi rychlé. Jejich charakteristické časy jsou menší než zlomky milisekund. Doba jeho chladnutí je naopak hodně dlouhá. V případě tohoto experimentu trvala zhruba pět minut, což je doba pokrytá měřením znázorněným na obrázku.
Závěr
V současné době se využívá také měď, stříbro nebo rhodium, tedy kovy. Mají tu výhodu, že jejich atomový magnetický moment je nulový. To je důležité proto, že jaderný magnetický moment je mnohem menší – asi o tři řády - než atomový (samozřejmě jen v případě, že ten není nulový. I právě jaderné magnetické momenty se využívají k rekordnímu dochlazování. Chlazení je založeno na odebírání energie spinovému systému pomocí jaderné adiabatické demagnetizace. Problém je pomalé nastolování termodynamické rovnováhy mezi spinovým systémem a mřížkou. Velmi intenzivní chlazení umožňuje pracovat v oblasti miliKelvinů a přiblížit se těsně k absolutní nule jak ze strany kladných, tak i záporných teplot. Rekordy v dosažených nejnižších teplotách se blíží k desítkám pikoKelvinů.
Zajímavé je studium délky doby chladnutí různých systémů od záporných teplot ke kladným. Mohlo by pomoci nalézt systém, který si udrží zápornou teplotu co nejdéle. Důležité je dosahování záporných teplot co nejbližších absolutní nule. Inspirující je i výzkum změn magnetických vlastností látek, které v podmínkách záporných teplot probíhají u kvantových spinových systémů. Není vyloučeno, že se v budoucnu najdou i zajímavé praktické aplikace takových systémů. Při objevu jaderné magnetické rezonance se také nedalo předpovídat, jak široké nalezne uplatnění třeba v medicíně.
Velmi podrobný a dobře napsaný přehled problematiky publikoval A. S. Oja a O. V. Lounasmaa v Reviews of Modern Physics.
Fyzici pronikli do říše divů a poprvé pozorovali „Alenčiny prsteny“
Autor: Stanislav Mihulka (30.08.2023)
Strukturovaný materiál po 266 letech skoncoval s Leidenfrostovým jevem
Autor: Stanislav Mihulka (01.02.2022)
Wu-chan opět středem zájmu, tentokrát kvůli textilii „radiační metatkanina“
Autor: Josef Pazdera (10.07.2021)
Teplota mozku
Autor: Josef Pazdera (02.06.2021)
Nejčastější chyby při screeningu horečnatých stavů pomocí termokamery
Autor: Jan Sova (10.11.2020)
Diskuze:
Realita magnetického pole, definice teploty atd.
Tomáš Brauner,2011-01-12 22:37:26
Chtěl bych reagovat ke každému trošku, takže založím nové vlákno. Nejdřív pro pana Ka: psát, že magnetické pole není reálné a nemůže konat práci, je úsměvné. Zkuste si třeba zalézt do tomografu s kovovými hodinkami a uvidíte. Ta stránka, na kterou odkazujete, popisuje jen případ částice bez spinu v magnetickém poli, kdy se práce skutečně nekoná. Částice se spinem (což je drtivá většina) ale mají magnetický moment. Ten bude v magnetickém poli naklápěn, případně vtahován do oblasti se silnějším polem, přičemž se práce samozřejmě koná,
Jinak k definici teploty. Nevšiml jsem si, že by to v diskusi někdo zdůraznil přede mnou, ale ve statistické fyzice skutečně existuje zcela obecná definice, která říká, že v termodynamické rovnováze se statistické obsazení jednotlivých energetických hladin systému řídí Boltzmannovým rozdělením, tj. pravděpodobnost obsazení hladiny s energií E je úměrná exp(-E/T).
Tato definice jednak ukazuje, proč je vhodnější pracovat s převrácenou teplotou než s teplotou samotnou - obsazení hladin, energie systému, stejně tak jako dalši termodynamické veličiny se mění zcela spojitě, když přejdeme z velkých kladných teplot do velkých záporných (1/T prochází nulou).
V různých speciálních případech tato obecná definice samozřejmě přechází na definice, zmíněné tady dříve. Například v případě ideálního atomového plynu je energie uložená jen v translačním pohybu atomů. Celková energie se ukazuje být úměrná teplotě. To ale samozřejmě neznamená, že by v oněch spinových systémech byla i energie záporná. Prostě tam neplatí přímá úměra mezi teplotou a celkovou energií.
Další výhoda statistické definice teploty je, že platí beze změny v klasické i kvantové fyzice a lze ji aplikovat jak na makroskopické objekty - kde souhlasí s termodynamickou definicí, formálně shrnutou v předchozím vláknu - tak na extrémně kvantové systémy, což je právě případ oněch spinů s pouhými dvěma stavy.
V reálných systémech člověk musí dbát, aby byla alespoň přibližně ustavená tepelná rovnováha, což rozebral pan Wagner velmi důkladně ve svém článku, ale co se týká formální definice teploty, o té není pochyb. Existují i různé jiné, fenomenologické (a praxi bližší) definice, ale ty mají jen omezený obor platnosti. Tam, kde je lze aplikovat, ale musí všechny definice dát stejný výsledek.
Definice teploty
Petr Slavík,2011-01-11 10:48:40
V základních učebnicích thermodynamiky se ukazuje, že Pfaffova diferenciální forma (pro případ definice reversibilně přijatého/odebraného tepla) má integrační faktor. Faktor, který je roven reciproké absolutní teplotě (blíže viz Carathéodorovy věty). Viz. exaktní diferenciální rovnice a totální diferenciál.
Každá reálná termodyn. rovnováha je metastabilní
Vladimír Wagner,2011-01-11 08:31:51
I zmiňovaný horký čaj bude bez ohřívání ztrácet energii a chladnout. Termodynamická rovnováha je metastabilní. Přesto je u něj teplota dobře definovaná a měřitelná. Úplně stejně je to u popsaných kvantových systémů. Pokud jim nebudeme dodávat energii (aktivně udržovat), tak budou chladnout, jak je popsáno v článku. A tak tomu bylo v popsaných experimentech. Pro spin částic 1/2 máte třeba jen dvě hladiny. Pro dosažení záporné teploty nekonečně se blížící absolutní nule opravdu potřebujete nekonečnou energii, ale metastabilní termodynamickou rovnováhu pro jiné záporné teploty můžeme dostat (jak ukazují popsané experimenty). Ztráta energie spinových stavů přechodem k jiným stupňům volnosti je totiž velmi pomalá.
ztráta
Petr Ka,2011-01-11 08:45:29
Jenže ta ztráta energie při dodávání (celé aparatury) je mnohem větší. Takže když si vyberu pouze dvě hladiny, tak na nich dokážu leccos. Je to jako pro normální systém v rovnováze s dvěma částmi s různou teplotou. V jedné části si vyberu jednu hladinu (vyšší u vyšší teploty) a ve druhé druhou. Budu-li se dívat pouze na ně ("filtr"), dostanu inverzi. Ovšem všechna zařízení s "negativní teplotou" (masery/lasery) pracují se značnými (a rychlými) ztrátami.
Je to prostě minimálně nestandardní, když fyzika matematice "říká", že záporné (teploty či cokoli) jsou větší než kladné. Je to snaha zaujmout (publikovat) a ne o nutné a konstruktivní řešení.
metastabilita
Petr Ka,2011-01-11 08:58:45
Je-li laser (s dobou inverze ns či až v řádu fs) metastabilní, tak je pak vše stabilní (stále platí v infinitesimálních krocích minimální akce). Pak jde jen o to, jaký systém si volím, a tak dosahuji čehokoli, kdyź si to definuju jakkoli ("neklasicky", "neortodoxně").
ztráta
Petr Ka,2011-01-11 11:31:53
Ale dodávání energie u laserů (či maserů) čerpáním přes jinou hladinu je mnohem rychlejší (+ značné ztráty) než přechody u uvažované "laserující" dvojhladině (se zápornou teplotou - inverzí obsazení). Tedy udržující interakce s okolím jsou rychlejší a nejde o rovnováhu (v normálním smyslu definice). Je třeba také vyšetřovat jiné derivace ... A pokud z nelineárního systému (protože takový musí být k inverzi) v úvaze "vytrhnu" část, tak díky neaditivitě dostávám záporné hodnoty (někdy i pravděpodobnosti a jiných valičin).
laser/maser
Petr Ka,2011-01-11 12:03:31
"Záporná teplota" je dosahována v laseru(http://en.wikipedia.org/wiki/Negative_temperature). Ovšem každý funkční laser je zkonstruován kromě "ziskového prostředí" (nejde o perpetum) i z energetického čerpání (dalších hladin) zajišťujícího inverzi(http://en.wikipedia.org/wiki/Laser_construction) a z rezonátoru (filtru, který nám ukazuje jen danou frekvenci laserujícího záření). Nejde o zesílení ("rovnováhu", inverzi) z ničeho, ale o záměrně (a rychleji) silou udržovaný stav.
Relaxační doba je v řádu minut
Vladimír Wagner,2011-01-11 14:20:18
Jak je v článku psáno, tak relaxační doba spinových systémů zkoumaných v popisovaných experimentech je v řádu minut. Tedy chladnutí takového systému bez dodávek energie (žádné čerpání energie přes jiné stavy...) trvá tuto dobu (viz i obrázek v článku). V těchto experimentech není využíván laser. Ostatně v době toho prvního zkoumání záporných teplot (1951) ještě ani lasery nebyly (první maser 1953 a laser 1960). Minutový relaxační čas je opravdu dostatečně dlouhý k dosažení velmi kvalitní metastabilní termodynamické rovnováhy.
jde o princip
Petr Ka,2011-01-11 15:32:55
I ve zde zmiňovaném článku o první dosažené populační inverzi (princip jako v laseru) - (1951 E. M. Purcell a R. V. Pound) - je čerpání (jeho časová konstanta) rychlejší (puls elamg. záření) a relaxace na (jako laserující) "dvojhladině" pomalá. Kdyby bylo čerpání pomalejší, tak nelze dosáhnout inverze. V článku dochází k "odpojení" zdroje čerpání(jak končí puls). Dochází tedy ovšem k ustavičnému poklesu teploty (relaxace) díky nevyváženému potenciálu (proti podmínce rovnováhy - http://en.wikipedia.org/wiki/Thermodynamic_equilibrium). Je to jako vystřelit kuličku do stropu a její pád považovat za rovnovážnou relaxaci.
Nic to ale nemění na tom, že je zbytečné zavádět nelineární stupnici (dokonce se singularitou). Pro měření je vždy důležitá linearizace (Kelvin).
Pulzy proměnného pole jen měří teplotu
Vladimír Wagner,2011-01-11 16:23:30
Systém se zápornou teplotou se dosahuje překlopením pole. Pulzy proměnného magnetického pole jsou jen pro měření teploty. I u horké vody dochází k ustavičnému poklesu teploty. A poměr mezi rychlostmi, tou se kterou se termodynamické veličiny (teplota ...) ve vodě vyrovnávají ku té, se kterou předává voda teplo do okolí (chladne), není zase tak rozdílný od poměru mezi rychlostí vyrovnávání termodynamických veličin (teploty ...), tedy spin-spinové interakce, a relaxace (chladnutí) popsaného kvantového systému. I chladnutí hrnku s vodou budete považovat za něco jako pád kuličkÿ vystřelené ke stropu?
anti
Petr Ka,2011-01-12 07:38:48
Stále ale jde v případě spinů o nevyrovnaný potenciál (je jedno, jaký je počet částic). V chladnutí hrnku jednotlivé částice vzájemně reagují mnohem rychleji než je časová konstanta chladnutí. Ale u atomů/častic v metastabilním stavu nedochází k vzájemným interakcím (nebo zanedbatelně pomalu) a pád na nižší hladinu je rychlejší (jde vlastně téměř o vzájemně izolované částice). Je to jako ono vystřelování nezávislých kuliček do stropu. Nelze pak ze signálu (poměr nárazů do stropu a na podlahu) říci, že po vypnutí střelby do stropu (nebo otočení místnosti - pole), je u stropu více kuliček, a tak zde musí být nějaká anti-gravitace, která je tam "drží" (záporná teplota). To, že téměř nedochází k výměně s okolím (např. tření ve vzduchu při pádu), nezaručuje správnost úvah (že jde o rovnovážný stav a něco "negativního").
Tak konečně vím, proč to nechápete
Vladimír Wagner,2011-01-12 08:35:26
Vážený pane Ka, teď konečně vím, proč to nechápete. Vy si pořád myslíte, že jádra ve spinových stavech spolu neinteragují. Ale to mě nemohlo napadnout, vždyť v článku i diskuzi jsem mnohokrát napsal, že interagují a mnohem rychleji než s jinými stupni volnosti. Tedy vyrovnání teploty přes interakci (výměnu energie mezi spinovými stavy) je mnohem rychlejší. Teď cituji z článku: "Procesy interakce mezi spiny, které nastavují termodynamickou rovnováhu ve spinovém systému, jsou velmi rychlé. Jejich charakteristické časy jsou menší než zlomky milisekund. Doba jeho chladnutí je naopak hodně dlouhá (minuty)." Při popisu v prvním článku jsem pak explicitně celý proces popisoval: "Důležité pro možnost hovořit v tomto případě o teplotě je, aby si částice předávaly orientaci spinu a energii s tím spojenou. Pokud změní jedna částice energeticky náročnější spinovou orientaci na méně energeticky výhodnou, uvolní se přesně taková energie, aby jiná částice, která ji převezme, změnila spinovou orientaci v opačném směru. Tato předávání orientace a energie musí probíhat dostatečně rychle, aby se v systému mohl nastolit stav termodynamické rovnováhy s definovanou spinovou teplotou. Jedná se o analogii předávání energie ve srážkách atomů (molekul), které vede k termodynamické rovnováze v systému s klasickou teplotou." V případě našich experimentů si různě orientované "jaderné magnetky" vyměňují energii mezi sebou prostřednictvím magnetického pole. A tato výměna je o mnoho řádů rychlejší než předávání jejich energie jiným stupňům volnosti mříže (vibrace a rotace molekul či atomů), které způsobuje ztrátu energie ve spinovém systému a chladnutí. Jsem rád, že jsem zjistil, kde jste věc nepochopil. A že už Vám bude situace jasná. Omlouvám se Vám i čtenářům, že to trvalo tak dlouho. Ale mě fakt nenapadlo, že si myslíte, že mezi jádry ve spinovém stavu nedochází k interakci, když v článku a diskuzi jsem nejméně desetkrát opakoval, že je jejich interakce silná a charakteristické časy výměny energie mezi nimi velmi krátké. A i v odkazovaných odborných článcích je toto uváděno a zdůrazňováno, jako ta základní podmínka, která musí pro dané systémy platit. Takže lze naši diskuzi uzavřít a děkuji za ni. Možná i některým jiným čtenářům pomohla objasnit některé termodynamické pojmy a díky ni mám o jeden článek na Oslovi, který bych jinak nenapsal, více :-)
Ještě k popisu bez přechod nekonečnem
Vladimír Wagner,2011-01-12 08:53:17
Ještě malý komentář k Vaší poznámce : "Nic to ale nemění na tom, že je zbytečné zavádět nelineární stupnici (dokonce se singularitou). Pro měření je vždy důležitá linearizace". I v článku a v diskuzi (pan Petr Zima) se uvádí, že lepší pro popis takového systému je převrácená hodnota teploty (přechod přes nulu a v místech absolutní nuly v teplotě máme na jedné straně plus a na druhé mínus nekonečno. Problém při používání této veličin v popularizačním článku je, že pro laiky je převrácená teplota hůře představitelná než teplota.
Magnetizmus
Marek Fucila,2011-01-12 10:30:05
Pan Wagner, ja by som sa chcel opytat na ten spin. Z Vasho vysvetlenia panovi Ka sa mi zda, ze som tiez celkom dobre nerozumel magnetickemu polu. Ak Vas spravne chapem, tak vlastne magneticke pole neposobi priamo na kazde jadro atomu, ale postupne si (zrejme vymenou nejakych castic) jednotlive atomy vymenia informaciu o polarite mexzi sebou. A kedze sa pri tom spotrebuje alebo uvolni energia, mozeme to chapat ako zmenu teploty systemu.
Cize zmenu spinu konkretneho atomu niekde v strede kristalu zabezpeci niektory z jeho susedov? To externe magneticke pole, ktore sa zmeni posobi na atomy v strede len sprostredkovane?
magnetismus
Petr Ka,2011-01-12 10:40:13
Magnetickou interakci však nelze považovat za reálnou (navíc je její vliv většinou v NMR zanedbatelný, pokud nejde o krystal, díky krátkodosahovosti). Magnetické pole je jen zdánlivé (relativistický jev http://en.wikipedia.org/wiki/Li%C3%A9nard%E2%80%93Wiechert_potential - takže tak zdánlivé jako třeba Coriolisova síla) a proto také nekoná práci (http://en.wikipedia.org/wiki/Magnetic_field - "a magnetic field is dependent on the reference frame of the observer", http://stupac2.blogspot.com/2007/04/magnetic-fields-do-no-work.html). Nelze je tedy považovat za přechod odstraňující potenciálovou nerovnováhu, ale pouze jde o "formální" transformaci souřadnic (i když pěkně pokřivenou).
Nesmysl o magnetickém poli
Petr Karel,2011-01-12 13:23:32
Na okraj k předchozímu příspěvku: Obecně tvrdit, že magnetické pole nekoná práci, je nesmysl. Je pravda, že magnetická Lorentzova síla působící na nabitou částici práci nekoná, ale magnetické pole působící na vložené magnetikum práci konat může.
Spin-spinova interakce
Vladimír Wagner,2011-01-12 14:01:00
Vazeny pane Fucila, je treba zduraznit, ze v dane chvili pusobi na system vice magnetickych poli. Vnejsi magneticke pole je dulezite pro vytvoreni systemu s dvema (pro spin 1/2) energetickymi hladinami. Dalsi je spojeno s jadry a jejich spinem (magnetickym momentem). A prave toto, ktere je spojeno s "magnetkami" jader je dulezite pro nastolovani termodynamicke rovnovahy. Jak uz pripomel pan Ka, je kratkodosahove. Proto se pri popisovanych experimentech pouzivaly vzdy krystaly ci kovy, jak se v obou clancich zduraznuje. V techto systemech je vsak interakce spinu (magnetickych momentu) intenzivni a rychle navazuje termodynamickou rovnovahu. Musi se tedy pouzivat materialy ze specifickymi magneticke vlastnosti. Ale je jich dost a v nich trva nastolovani termodynamicke rovnovahy prostrednictvim spin-spinove interakce zminene zlomky milisekund a chladnuti naopak zminene minuty.
re nesmysl
Petr Ka,2011-01-12 15:26:45
Jak je uvedeno v dříve uvedeném odkazu (http://stupac2.blogspot.com/2007/04/magnetic-fields-do-no-work.html), tak práci lze mag. polem konat, ale pokud dochází k disipaci (ke "ztrátám"). V ideálním případě nikoli (i pro nějaké magnetikum - viz pokusy o perpetum). Ovšem tato disipace by byla zde musela být rychlá (rychlejší než onen metastabilní stav) a nešlo by pak o rovnováhu (s elektromagnetem mohu na skládce vykonat práci, ale jde i o ty ztráty a jejich rychlost).
Také to nemění nic na tom, že u maseru/laseru k žádné rychlé interakci účinně nedochází (např. kolize v plynu, které by ničily inverzi), a přesto se mluví o záporné teplotě. Je-li to správné, tak je třeba ukázat i zde, že je zde rovnováha, pokud chceme mluvit o rovnovážné teplotě. Podle mého jde o nerovnovážnou termodynamiku.
A co se týče "rozšíření" pojmu. Já vyžaduji po definici (například metru), aby platila vždy a všude. Je-li definice různá, musí jít (alespoň někde) i o různá řešení.
re
Petr Karel,2011-01-12 16:52:45
Vyžadujte si po definici, co chcete, ale nedivte se, že Vám pak mnohé části fyziky nebudou vonět, fyzikální realita není ideální konstrukt. Zmínka o perpetuu mobile je mimo mísu, nikdy jsem netvrdil, že se koná práce "z ničeho". Vtahování/vysouvání magnetika do/z nehomogenního magnetického pole (podle znaménka susceptibility) je způsobeno změnou vnitřní energie spočívající v rozdílné magnetizaci a u lineárních magnetik nemusí být spojeno s disipací, ale může být vratné. Jiný názornější příklad: můžete si jedním magnetkem posouvat druhý magnetek (budou-li vhodně natočeny stejným pólem k sobě) a magnetickým polem tak na něm konat práci. A místo nějakého blogu se doporučuji spíše podívat do některé učebnice elektřiny a magnetismu.
re re
Petr Ka,2011-01-13 08:03:17
Jakékoli magnetické pole (z obecné definice, které tak nemáte rád) je pouze transformací souřadnic (viz výše), takže chtít po formální transformaci práci je právě generování práce z ničeho (je to v míse).
Posouváte-li magnetem jiný magnet, tak vykonáváte práci rukou (aktuátorem), ale ne magnetickým polem (je to jako říci, že šňůrka joja vykonává práci). A co se týče vsunování do magnetického pole, tak aby šlo o vratný děj (http://en.wikipedia.org/wiki/Reversible_process_(thermodynamics) ), tak je třeba být neustále v termodynamické rovnováze (o čemž tady diskutuju, pak by také byla možná práce). Ale z principu (viz Maxwellovy rovnice) to možné není. Aby došlo k přeměně energie vkládání (ideálně pro supravodiče http://en.wikipedia.org/wiki/Superconducting_magnetic_energy_storage) do systému, tak je nutné vytovření elektrických proudů (ale na magnetické pole celkově nic nezbývá). Magnetismus je stále jen transformace. Je to jako začít padat do Slunce a z frekvenčního posuvu říci, že se Slunce ohřálo ("vykonal" jsem mnohem větší práci).
Toto ale už k článku tak nepatří, takže už přestávám reagovat.
znovu
Petr Ka,2011-01-11 07:52:24
Pomineme-li fakt, že "teplotu můžeme definovat různými způsoby" znamená pak vnitřní rozpor, tak je také nutné říci, že reálné systémy nemohou mít (v celém energetickém spektru) omezený počet hladin (a při dodávání energie k dosažení inverze v rovnováze je nutno na nekonečně hladin nekonečného úsilí - nekonečno je tedy také nedosažitelné jako 0K). Je to jako s umělou optickou/akustickou černou dírou. Neznamená to, že byla laboratorně stvořena singularita (nekonečno), ale v (námi) omezeném spektru frekvencí se systém chová obdobně (ale nedokonale). Dosažení je formální v tom, že když vyfiltrujeme (či neuvažujeme) ostatní stavy, tak pro nějaké a s obměněnou definicí teploty dostaneme (dočasně) záporné teploty (nebo záporný index lomu metamateriálu složeného z materiálů s kladnými indexy lomu). Také je třeba zdůraznit, že jde minimálně o "nestabilní rovnováhu" (labilní stav, který je třeba aktivně udržovat).
re
Petr Karel,2011-01-12 13:59:41
To, že nějakou veličinu lze definovat různými způsoby, neznamená žádný vnitřní rozpor. Nejsme v matematice a nedefinujeme ideální struktury. Fyzika si hledá pojmy a veličiny, dobře popisující realitu. Je třeba se smířit s tím, že pro fundamentální veličiny (délka, čas, energie, síla, teplota...) nelze vytvořit definici v matematickém smyslu. Některé takové veličiny jsou zavedeny intuitivně, zavedení některých připomíná definici kruhem, u některých veličin dosud nejsou vyjasněny extrapolace zavedení v běžných podmínkách na extrémní situace (relativistická teplota). U různých verzí "definic" jedné veličiny je potřeba dbát na to, aby ve všech situacích, kdy je rozdílná definice možná, byly různé způsoby zavedení konzistentní, tj. aby dávaly stejné výsledky (případ absolutní a termodynamické teploty). Některé definice představují samy o sobě (např. radiační teplota, efektivní teplota, jasová teplota, barevná teplota) ROZŠÍŘENÍ nad původní rámec pojmu (nerespekrují některé podmínky "klasičtějších" definic) či je lze použít pro ROZŠÍŘENÍ daného pojmu do oblasti, kde např. jiné definice nelze z různých důvodů použít. Záporné teploty představují takové rozšíření STATISTICKÉ definice teploty do oblasti systémů s konečným počtem energetických stavů příslušným danému stupni volnosti.
Pomineme-li zmínění onoho "vnitřního rozporu", zdá se z posledního Vašeho příspěvku, že pomalu začínáte autora chápat. Jsem rád, že jeho příkladná snaha zodpovídat diskusní otázky nebyla marná. Moc mu za ni děkuji.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce