
V roce 1912 polský fyzik Marian Smoluchowski navrhl provést pokus v němž by nepatrné, všemi směry se pohybující partikule měly roztočit lopatky větrníku a na něj napojené ozubené kolo. Nejdůležitější součástkou tohoto řešení byla západka, která bránila kolu nabývat zpětného chodu. Nápad to byl geniální, ale známý fyzik Feynman na svých přednáškách po Druhé světové válce dokazoval, že to je nesmysl a že takový stroj v jednom systému pracovat nemůže.
Nová mašinka, jejíž popis se nyní objevil v časopisu Physical Review Letters, se navzdory skeptickým předpokladům přece jen točí.
Feynmannova rohatka se nemůže nikdy točit
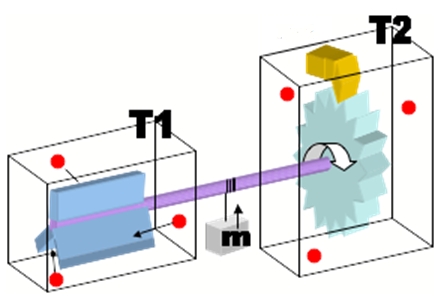
Molekuly plynu v levé nádobě narážejí na lopatky a způsobují otáčení hřídele. Západka v pravé nádobě je tlačena pružinou k ozubenému kolu a zabraňuje zpětnému otáčení. Mezi nádobami je na hřídeli připevněna kladka, na níž se navíjí vlákno se závažím. Feynman nejprve uvažuje případ stejných teplot plynu v obou nádobách. Pružinu v pravé nádobě ale není možné vyčlenit z tohoto dění a tak vlivem nárazů molekul musíme počítat se samovolným stlačením pružiny, a tedy i samovolným oddálením od ozubeného kola. To znamená, že bude kolo „prokluzovat“ a otáčet se nežádoucím směrem. K přeměně tepla (kinetická energie molekul plynu v levé nádobě) na práci (zvedání závaží) tedy nemůže dojít.
Feynman ve svých úvahách pokračoval a předpokládal, že by teplota plynu v levé nádobě byla vyšší než teplota plynu vpravo. Pak by fluktuace pružiny již nestačila kompenzovat účinek a zařízení by se začalo otáčet. To ale není perpetum mobile v podobě Maxwellova démona, ale jde o pouhou modifikaci Carnotova stroje, při němž je teplota plynu (kinetická energie) přeměněno na práci.
A přece se točí ?
Pokus, který nyní uskutečnil Devaraj van der Meer se svými kolegy z nizozemské University of Twente ukazuje, že se varianta takové rohatky točí. Základem jejich ukázky je jakási třepající se plošina, která vytváří náhodný pohyb skleněných kuliček. Ty skáčou všemi směry, jako když v mikrovlnce vyrábíte popkorn. Kuličky dopadají na lopatky „větrníku“ a roztáčí jej. A protože je pohyb jednosměrný, zdá se, že by šel využít k něčemu užitečnému.
To, co na pokusu vědci od dob Fenmana změnili, se týká vrtulky, která již není vybavena západkou bránící zpětnému pohybu. Vylepšení se týká samotných lopatek. Pokus ukázal, že když jsou lopatky z obou stran stejné, náhodně dopadající kuličky větrník neroztočí. Když na jednu stranu lopatek přilepili vroubkovanou tapetu, vrtulka se roztočí. Jde o to, že vroubkování udělá povrch lopatky pro dopadající kuličky měkčí.
Je známo, že náraz do měkkého je z hlediska předání energie „výnosnější“ a právě tím se neuspořádaný pohyb kuliček postará o roztočení vrtulky. Jakmile ale k tomu dojde, kuličky se také začnou točit. Jde o zpětnou vazbu mezi roztočenými lopatkami a okolním prostředím. Je to nutná reciprocita vztahu má dáti, dal - kuličky roztočí vrtulku a ta roztočí kuličky. A právě něco takového by se mohlo dít v našich buňkách, jen v mnohem menším měřítku, tvrdí vědci.
K tomu aby se vrtulka roztočila, potřebuje předváděný přístroj hodně skákajících kuliček. To s sebou pochopitelně nese mnoho ztrát energie v důsledku tvorby tepla a zvuku. Když začnete počítat kolik energie je potřeba na vytvoření prostředí skákajících kuliček schopných pohnout lopatkami vrtulky, zjistíte, že jde o zařízení zcela neefektivní. Druhý zákon termodynamiky se jen tak obelstít nedá. Proto není tento pokus spolu s roztáčením narážejících kuliček, důkazem existence stroje k získávání energie z Brownova pohybu", o perpetum mobile nejde. Pokus je ale významný z jiného důvodu - může totiž ozřejmit pochody, které se dějí uvnitř buněk. Nabízí se srovnání s pohybem RNA polymerázy a její posun podél vlákna DNA když syntetizuje molekulu RNA a DNA slouží jako matrice.
Podobně jako polymeráza se chová protein kinesin, ten je zase základem takzvaných vnitrobuněčných molekulárních proteinových motorů, jež přemísťují mitochondrie a další organely jako třeba chromosomy. Kinesiny jsou přepravníky, bez nichž by buňky nebyly schopny provést mitózu ani meiózu a nemohly by se dělit. Nizozemský pokus nám podsouvá otázku, zda pohyby některých molekul v buňce nejsou založeny na principu využití náhodných pohybů a zda nejsou obdobou tzv. Freemanovy rohatky. Podle Meerse by jejich „makroskopický pokus“ měl přispět k pochopení enzymatických dějů, které probíhají uvnitř buněk a využívají principu Brownova molekulárního motoru.
VIDEO: Dva tisíce náhodně se pohybujících kuliček roztáčí ozubené kolečko proti směru hodinových ručiček:
Newly created machine from Science News on Vimeo.
Pramen: University of Tvente
Poznámka
Tak jako v práci Američanů, o níž jsme psali v článku „Navzdory Einsteinovým předpokladům“, ve které nešlo o popření Einsteinova fyzikálně-matematického popisu Brownova pohybu, tak ani v tomto případě z Nizozemí nejde o popření výpočtů Feynmana dokládajících neexistenci rohatky poháněné Brownovým pohybem. V obou případech jde jen o jistý druh nadsázky, kterou mateřská pracoviště objevitelů vtipně využila k upoutání pozornosti médií. To se jim sice podařilo, ale za cenu toho, že mnohé z agenturních zpráv, které věc podrobně nevysvětlují, jsou nesmyslné.
Se snahou pracovišť upoutat na sebe pozornost za každou cenu, se zřejmě budeme setkávat často.
Diskuze:
Všechno špatně!
Tomáš Brauner,2010-06-18 11:53:16
Navazuji sice na debatu s panem Brožem ohledně významu rotace kuliček pro fungování experimentu, ale protože přidávám některá nová (dle mého překvapivá) fakta, dovolil jsem si příspěvek zařadit na začátek diskuse.
Především se omlouvám za blábol, co jsem napsal včera. Článek ve Phys. Rev. Lett. jsem jen přelétl a výsledkem bylo ukázkové nepochopení psaného textu, neboli jsem si naběhl :-) Pane Broži, chcete-li si ten článek přečíst už teď, pošlete mi svůj e-mail na tom.brauner na Seznamu. (Je přece jen chráněný autorskými právy, proto ho nechci vyvěsit tady či jinde úplně veřejně.)
Díky za Vaše vysvětlení, jak může docházet k nesymetrickému rozdělení rotace kuliček. Nicméně stále si myslím, že ta rotace nebude hrát podstatnou roli, viz níže. Ale naprosto se s Vámi shodnu na tom, že experiment nelze popsat jen pomocí analogie s proudící tekutinou na základě tvaru či povrchu lopatek. Termodynamika není zrovna můj obor, takže jsem se z Vašeho rozboru leccos dozvěděl :-)
1) A teď to, co mi včera uniklo: experimentálně pozorované konvekční proudění kuliček má STEJNÝ směr jako rotace lopatek! Jde totiž o pozitivní zpětnou vazbu. (Volně dle publikovaného článku.) Jednak rotující lopatky předávají kuličkám větší impuls ve směru rotace než proti směru a vyvolají tedy cirkulaci kuliček ve stejném smyslu. Na druhou stranu, část kuliček je vždy "uvězněna" mezi horními dvěma lopatkami. Když se vrtulka pootočí a kuličky se tak "vysypou", zvýší se tím výrazně hustota kuliček na této straně lopatek. V důledku toho se zde kuličky vzájemnými srážkami zpomalí a předají lopatkám menší impuls než rychlejší kuličky na opačné straně lopatek. Tato zpětná vazba způsobí, že vrtulka se bude roztáčet (náhodně v jednom či druhém směru) i BEZ asymetrické úpravy povrchu lopatek. Jakmile jednou v důsledku fluktuace v rozdělení kuliček začne rotovat, tento efekt ji bude v rotaci udržovat, dokud jiná fluktuace neobrátí její směr. Úprava povrchu jedné strany lopatek pak jen způsobí (stejným mechanismem jako u Nicholsova radiometru), že se vrtulka bude častěji roztáčet jedním preferovaným směrem.
2) Tento efekt zpětné vazby mezi kuličkami a vrtulkou zmizí, když otočíme osu vrtulky vertikálně. (Autoři to zkusili!) To samozřejmě neznamená, že by se vrtulka nezačala točit, když budou mít lopatky na svých stranách různý povrch, rotace ale nebude stabilizovaná vzájemným působením s kuličkami. Takže gravitace tady opravdu hraje důležitou roli, ale ne díky změně rozdělení rychlostí kuliček, jak zde někteří navrhovali, ale díky tomu "uvěznění" kuliček mezi horními dvěma lopatkami.
A jak je to tedy se zákonem zachování momentu hybnosti? Jak je možné, že kuličky cirkulují souhlasně s rotací vrtulky? Dle mého je to prostě tím, že díky nesymetrickému rozdělení hustoty a rychlostí kuliček je do systému pumpován moment hybnosti tou vibrující deskou, která udržuje kuličky v pohybu. Vlastní rotace kuliček nebude podle mě hrát významnou roli. Dovolím si hrubý odhad. Dle autorů je moment setrvačnosti vrtulky 7.2x10^(-5) kg m^2. Kuličky mají průměr 4 mm a hustotu 2.6 g/ccm. Poměr momentů setrvačnosti vrtulky a jedné kuličky tedy bude cca 5x10^5. Kuliček je řádově tisíc, pořád z toho ale vychází, že kdyby měly kompenzovat moment hybnosti samotné vrtulky (neuvažuji vůbec tu konvekci!), musely by rotovat zhruba 500x rychleji než vrtulka, tj. frekvencí řádově 100 Hz.
Děkuji moc za informace přímo ze zdroje
Pavel Brož,2010-06-19 00:02:07
Rád vám napíšu na Váš mail. Pracuji v komerční sféře, institucionální přístup k fyzikálním odborným časopisům bohužel nemáme. Zase máme přístup třeba k dokumentaci IBM k posledním verzím jejich systémů, tedy naprosto rozumím tomu, že ne všechny informace jsou volně přístupné a respektuji to.
Takže nakonec pozitivní zpětné vazba a konvekce ve směru otáčení lopatek, nikoliv v protisměru, jak jsem předpokládal. Tak takovéto chování systému bych opravdu nepředpokládal, a myslím si, že pro hodně i velice dobře se ve fyzice orientujících lidí je to opravdu nečekané. Nemůžu si pomoct, ale je to vynikající ukázka toho, jak i velice prosté systémy mohou svou dynamikou překvapit.
naběračka
Jan Kment,2010-06-17 15:42:58
S tou naběračkou je to opravdu trochu jiné. Pokud bydete mít absolutně tvrdé kuličky, absolutně tvrdou naběračku matematicky dokonalou osu a navíc zamezíte násobnému odrazu uvnitř naběračky jakož i vzájemnému mezi kuličkami a samozřejmě ve vakuu, pak by si, čistě laicky posouzeno, opravdu mohly být síly přenášené na dutou i vypuklou stranu rovné. Žádná z těchto podmínek se mi ale nezdá být splněna. Je li jeden z povrchů pružný a nerovný pak to podle mě znamená že se značná část sílového impulzu dopadající kuličky obrací kolmým směrem, čili to samé co se děje s tekutinou v naběračce, jenom jinak ošetřeno.
Zní to sice přesvědčivě, ale
Pavel Brož,2010-06-18 01:37:55
stále musím trvat na tom, že na toto konto byla napsána nepředstavitelně velká hromada článků už v první polovině minulého století. Souvisí to právě s tím mechanickým Maxwellovým démonem. Samotná geometrie těch lopatek k výsledku nevede, pokud uvažujete systém ve stavu termodynamické rovnováhy. Vždycky se nakonec došlo k závěru, že se to točit nebude.
Ona ta Feynmanova rohatka se západkou není o nic horší mechanismus. A ač se to zdá na první pohled sebevíce nepochopitelné, ta západka ve stavu termodynamické rovnováhy přestane jakožto západka fungovat. Čehož exaktní důkaz bohužel opravdu není triviální.
Mimochodem, ten přístroj v článku byl postaven právě kvůli ilustraci mechanismů probíhajících při tepelném pohybu molekul. Sami autoři použili přirovnání k Feynmanově myšlenkovém pokusu s rohatkou a západkou. To, že jejich přístroj na rozdíl od rohatky se západkou funguje, se děje na konto jakéhosi vtipně skrytého "podvůdku" - přístroj totiž není dokonalým simulátorem částic v tepelné rovnováze. To je důvod, proč tento experiment nevyvrací ani druhou větu termodynamickou, ani není realizací mechanického Maxwellova démona. To ale neznamená, že tady jiné záměrně volené podobnosti s tepelným pohybem částic nejsou, a bylo by chybou tyto podobnosti deklasovat nekorektními příměry s poměry platnými při obtékání tekutin.
Pavel Brož,2010-06-18 01:39:28
(omylem jsem to odklepnul před dokončením, omlouvám se)
V ohromném množství článků je dokazováno, že v termodynamické rovnováze nezáleží ani na tvaru lopatek, ani na jejich drsnosti, že nepomohou ani žádné rafinované mechanismy typu rohatek (tj. ozubených koleček s asymetricky skosenými zuby) a západek (které mají právě zapadáním na těch asymetrických zubech bránit těm ozubeným kolečkům v otáčení). Ve všech těchto věcech je spousta anti-intuitivních výsledků, které se nedají jednoduše vysvětlit, je možné těmto výsledkům buď pouze uvěřit, anebo se vrhnout do jejich studia.
Každopádně ale nelze přijmout sebepřesvědčivější argument postavený pouze na tvaru, povrchu či pružnosti materiálu, protože toto všechno samo o sobě nestačí na to, aby se to točilo. Klíčové je, že systém není v termodynamické rovnováze, a to tady od nikoho ze zdejších proponentů geometrických přístupů nezaznělo. Ne tvar lopatek, ale absence termodynamické rovnováhy je tím hlavním ve fungování toho přístroje. V tepelné rovnováze by to nefungovalo. Přitom ten přístroj je postaven jakožto (byť záměrně nikoliv věrný na celých 100%) model tepelného pohybu částic. Pominout fakt, že právě tento malý deficit modelu v napodobení skutečného tepelného pohybu částic je motorem tohoto zdánlivého perpetum mobile druhého druhu, je opravdu nepochopením celého experimentu.
Jak větrník, tak vodní mlýnek se točí v uspořádaném proudu tekutiny, který má do modelu tepelného pohybu částic nekonečně daleko. Pokud tu tekutinu ale rozředíte do podoby velice řídkého plynu, odstraníte uspořádaný pohyb molekul plynu a ponecháte pouze jejich tepelný pohyb, rotace mlýnků a větrníků ustane. Potom opět můžete ten plyn opět zahustit do hustoty původní tekutiny, mlýnky a větrníky zůstanou nehybné.
Aha.
Jan Kment,2010-06-18 12:48:11
Zdaleka ne všemu o čem mluvíte rozumím (nevím co je Maxwellův démon, ani česká wikipedie to neví), ale v každém případě děkuju za trpělivost. Rozhodně je to velmi provokativní pokus.
Nejsem profesionál
Pavel Brož,2010-06-19 01:57:56
jsem jenom jedinec, který vystudoval teoretickou fyziku, z vážných finančních důvodů odešel záhy z akademie do komerční sféry, jako to víceméně z donucení udělala na začátku devadesátých let spousta lidí. Teoretická fyzika je stále mým největším hobby, ale bohužel mě neživí. Spousta profesionálů bude mít mnohem lepší přehled, mou drzost s vynášením zdejších soudů prosím berte jenom jak reakci na to, že jsem tady nenašel takový protinázor, který by zohlednil všechny nezbytné detaily problému, které by dle mého názoru zohlednit měl.
Co se týče Maxwellova démona, tak se jedná vlastně opět o jakési myšlenkové zařízení, podobně jako je rohatka se západkou, a je ještě staršího data. Vymyslel jej Maxwell před skoro půldruha stoletím (v roce 1867). Představoval si malilinký mechanismus - obrazně malého démona - který by hlídal u malého otvoru v přepážce rozdělující prostor v nádobě s plynem. Tento démon by měl mít tu vlastnost, že by např. rychlejší molekuly plynu nechal prolétávat otvorem jenom jedním směrem, a ty pomalejším jenom opačným. Anebo v jiné obměně nechal molekuly prolétávat jenom jedním směrem, a vždy, když by hrozil průlet molekuly směrem opačným, otvor by dočasně zavřel.
V konečném důsledku by to vedlo k tomu, že by se v jedné polovině nádoby koncentrovaly rychlejší molekuly, zatímco v druhé pomalejší. Anebo v obměněné variantě by se v jedné polovině nádoby hustil plyn, zatímco ve druhé zřeďoval. V obou případech by docházelo ke sporu s druhou termodynamickou větou. V prvním případě by se bez dodávání energie molekulám plynu tento plyn separoval na teplejší část a studenější část. Ve druhém případě by se opět bez předávání energie molekulám v jedné polovině nádoby zahušťoval, a ve druhé zřeďoval. V obou případech by pak šlo získávat mechanickou energii ze získaného rozdílu ať už teplot, nebo hustot – např. by stačilo do otvoru v přepážce umístit vrtulku, která by byla následně roztáčena nárazy molekul z hustější, resp. teplejší poloviny nádoby.
Takže existence Maxwellova démona by byla v příkrém rozporu s druhým termodynamickým zákonem. Existoval-li by Maxwellův démon, tj. jakýkoliv mechanismus, který by bez předávání energie jednotlivým molekulám dokázal otevírat a zavírat otvor v přepážce tak, aby ve výsledku docházelo k narůstání tepelných či hustotních nehomogenit v nádobě, tak by bylo možné sestrojit perpetuum mobile druhého druhu – tj. stroj, který dokázal cyklicky měnit tepelnou energii molekul na energii mechanickou. Což druhý termodynamický zákon zakazuje.
Maxwellův démon doznal v následné více než století dlouhé diskuzi mnoha obměn, v každé ale šlo o to, pokusit se vymyslet jakýkoliv způsob, který by rozdělování molekul plynu mezi dvěma polovinami nádoby umožňoval. Ekvivalentem je samozřejmě přímá konstrukce perpetua mobile druhého druhu – jakmile totiž získáte možnost čerpat mechanickou energii z tepelného pohybu molekul, můžete právě tuto energii využít na separaci těch molekul (separace molekul plynu na teplejší a studenější samozřejmě je bez problémů proveditelná, pokud dodáváte mechanickou energii, koneckonců na tomto principu funguje každá chladnička). Feynmanova rohatka se západkou je právě takovéto zařízení, které by umožnilo přímé čerpání mechanické energie z tepelné energie molekul, ovšem už dávno před Feynmanem bylo dokázáno, že žádná varianta takovýchto zařízení, ani jejich obměn s jakkoliv tvarovanými či povrchově upravenými vrtulkami, nemůže fungovat.
Ruku v ruce s novými návrhy Maxwellova démona vznikaly i první důkazy nemožnosti těch či oněch konkrétních konstrukcí. Nicméně ač bylo získáno obrovské množství významných teoretických výsledků, které za dosti obecných předpokladů vylučovaly existenci Maxwellova démona, univerzální důkaz dodnes chybí.
První pokusy o univerzální důkaz nemožnosti Maxwellova démona sledovaly mechanickou cestu. Kvalitativně jiným přístupem byl přístup informatický – vycházelo se z toho, že Maxwellův démon by pro svou funkci musel umět shromažďovat obrovské množství informací o pohybech jednotlivých molekul, což by vyžadovalo přísun energie právě pro toto průběžné monitorování pohybů molekul. V důsledku by vzrůstala entropie právě tohoto démona minimálně takovým způsobem, že entropie celkového systému plyn + démon by vzrůstala, což právě druhý termodynamický zákon říká (entropie je vnitřní mírou neuspořádanosti systému, může být např. svázána s neuspořádaným pohybem molekul, ve skutečnosti jde ale o obecnější a abstraktnější termodynamický koncept).
Paralelně s těmito pracemi začaly vznikat nezávislé práce zabývající se tzv. informační entropií. Ukázalo se, že informace jako taková úzce souvisí také s jistým druhem neuspořádanosti. Rozvoj těchto prací ukázal na hluboké netriviální souvislosti mezi informační a termodynamickou entropií, a tyto nové výsledky se samozřejmě promítly i do prací zabývajících se (ne)možností existence Maxwellova démona.
Bohužel stejně tak, jako u mechanistického přístupu, i zde se přes všechen pokrok v pochopení této problematiky nepodařilo získat naprosto univerzální důkaz neexistence Maxwellova démona.
Někdy koncem osmdesátých a začátkem devadesátých let se situace obrátila – místo prací dokazujících nemožnost existence Maxwellova démona se začaly pomalu objevovat práce dokazující, že za určitých velmi speciálních předpokladů by něco, jako je Maxwellův démon, ve skutečnosti fungovat mohlo, a že tedy by do té doby nezpochybnitelný slavný druhý termodynamický záon mohl mít docela dobře určité limity své platnosti. Začaly se objevovat názory, jestli třeba náhodou některé mikroorganismy anebo jejich substruktury nejsou takovými velice chytrými udělátky, které umí rafinovaně využívat lokálních fluktuací ke svému pohybu či k zabezpečování vlastních životně nezbytných dějů. Objevily se práce dokazující, že přece jen existuje principiální možnost reverzibilního procesu měření a tím pádem monitoringu pohybu molekul bez nutnosti dodávání energie.
Každá taková práce ale většinou spustila lavinu následných prací, které výrazně omezovaly či v krajním případě zneplatňovaly výsledky prací předchozích. Tato problematika dodnes není uzavřená.
Poslední výsledky profesora Čápka, které zmínil pan František Kříž, souvisely ještě s dalším přístupem k možné existenci Maxwellova démona. Jak známo, kvantová mechanika, která popisuje zejména malé systémy molekulárních rozměrů (ale v některých případech i makroskopické jevy, jako jsou supravodivost či supratekutost), je teorií značně odlišnou od pravidel platných pro klasickou mechaniku. Kvantové děje v principu umožňují existenci např. koherentních dějů, při kterých nedochází k disipaci, tedy ztrátám energie. Typickými případy koherentních dějů jsou právě jevy supratekutosti a supravodivosti, kdy v prvém případě supratekutá kapalina teče s naprosto nulovým třením, ve druhém pak elektrický proud teče s naprosto nulovým elektrickým odporem. S koherentními jevy je ale možné se setkat i v případě tzv. Bose-Einstenových kondenzátů a koherentní děje jsou také v centru pozornosti výzkumníků také pro potenciální využití v budoucích kvantových počítačích.
Profesor Čápek odvodil model, ve kterém dochází ke koherentnímu ději, ve kterém se opakovaně přenáší např. elektrony v jednom uspořádaném směru tak, že se na jednom místě naváží na „ocásek“ vhodně vybrané organické molekuly, změní tím lokální potenciál, který způsobí přesunutí ocásku s elektronem, na novém místě ale dojde k uvolnění elektronu, tím pádem k restaurování potenciálu a narovnání ocásku na původní místo, kde se děj opakuje zase s jiným elektronem (aspoň tak jsem tomu porozuměl při rozpravách se svým bývalým spolužákem, toho času doktorandem i prof. Čápka). Celé to může fungovat jenom za dosti specifických okolností, podstatná tam samozřejmě je i konkrétní interakce té organické molekuly s rezervoárem, v němž se tato molekula pohybuje.
Jak zmínil pan Kříž, profesora Čápka zajímalo, jestli právě něco takového nemůže fungovat aspoň u některých mikroorganismů či buněčných mikrostruktur. Pokud by tomu tak bylo, pak by to znamenalo, že díky miliardám let evoluce našly tyto mikroorganismy či mikrostruktury „mezeru“ v platnosti druhého termodynamického zákona – tj. způsob, jak po vzoru Maxwellova démona chytře využívat lokálních momentálních fluktuací ve svém okolí ke svému prospěchu. Tuto otázku už bohužel po odchodu prof. Čápka bude muset zodpovědět někdo jiný.
Skvělá exkurze!
Jan Kment,2010-06-21 14:04:06
A poměrně srozumitelná, díky.
Přiznám se, že stále trochu věřím v nějaké perpetuum mobile, ač je to možná nemoderní a je to víceméně otázka pojmů. Každopádně je jasné, že přírodě je vlastní pořádná míra nerovnováhy, jakási prapůvodní energie, a nám jde jen o to, ji najít v dostatečně usměrněné podobě a moc si při tom neublížit.
Přesto mi nějak připadá, že pracovní vytížení toho Maxwellova dveřníka by exponenciálně rostlo, s každým úlovkem by houstla tlačenice u dveří molekul které chtějí zpátky, kromě krátkého téměř bezpracného úspěchu na začátku, ale ten by byl tak nepatrný, že by nebylo zaručené zda a nebo kterým směrem se instalovaná turbína roztočí. Ale možná si to představuju moc jednoduše a každopádně to už určitě někoho napadlo.
Analýza
Frantisek Kriz,2010-06-16 17:17:15
Točí se to díky rozdílným vlastnostem povrchu lopatek jak píšou. Z jedné strany lopatky je ten odraz víc pružný než z druhé a proto je z každé strany jiný předaný celkový impulz za sekundu, tj síla. Nemá na to vliv gravitace (souhlasím s p.Brožem) ani se nejedná o využití fluktuace v rychlostech molekul (kuliček) jak by to mělo být u správného Maxwellova démona. Moc nerozumím vysvětlení p. Brože, že v tom hraje roli rotační energie kuliček. Možná ano ale mělo by to fungovat i bez ní si myslím. Představme si místo kuliček hmotné body s nulovým momentem setrvačnosti (nebo tuhé kuličky s veškerou hmotou uprostřed a nulovým momentem setrvačnosti). Taky by se to točilo a samovolný pohyb kuliček (bez té třepačky dole) by se zpomaloval a získávala by se tak mechanická energie ochlazováním lázně. Na molekulární úrovni víme, že to fungovat nemůže – ale proč? Je to protože nejde udělat molekulární lopatky s mechanicky rozdílnými povrchy? Nebo spíš že u zahřáté lopatky už je jedno jaký má povrch?
Úkol: Rozmyslete si
1.Jestli funkce tohoto stroje je v principu stejná jako u Crookesova radiometru?
http://en.wikipedia.org/wiki/Crookes_radiometer
2.Proč není?
Bohužel to není analogie Crookesova radiometru
Pavel Brož,2010-06-17 00:51:01
Jsem velice rád, že jste zde zmínil ony radiometry – přiznám se, že dodnes jsem je znal jen pod názvem sluneční mlýnky  Z dob studií vím, že existují dva typy těchto slunečních mlýnků, aspoň mě to bylo svého času prezentováno tak, že ten „dražší“ mlýnek měl v sobě velice dobré vakuum, zatímco ten „levnější“ či „pouťový“ mlýnek měl v sobě zdaleka ne tak dokonalé vakuum. Oba typy mlýnků měly lopatky z jedné strany černé a z druhé odrazivé. Pro informaci ostatních čtenářům popíšu, jak který fungoval.
„Dražší“ mlýnek (dle Vašeho odkazu tedy Nicholsův radiometr) se otáčel vlivem tlaku světla (tj. byl vlastně experimentálním důkazem toho, že světelné záření nese hybnost). Fotony o hybnosti p=h*f, kde h je Planckova konstanta a f frekvence světla, se odrážely od odrazivé strany lopatek (tím pádem tato strana získávala hybnost 2*p po každém odrazu fotonu), zatímco černou stranou lopatek byly pohlcovány (tím pádem tato strana získávala od každého dopadlého fotonu hybnost p). Rozdíl hybností obou stran byl tedy p ve prospěch odrazivé strany, tedy tento mlýnek se otáčel tak, jako by odrazivá strana byla vnitřní plochou „větrníkové naběračky“.
„Pouťový“ mlýnek (správně tedy Crookesův radiometr) se otáčí na opačnou stranu, a to díky tomu, že černá strana se rychleji zahřívá, díky tomu rychleji ohřívá přilehlou vrstvu vzduchu v nedokonalém vakuu, a díky intenzivnějším srážkám molekul této vrstvy vzduchu a molekul černé strany lopatky získává naopak ta černá strana větší hybnost, než ta lesklá (ta zde ani nemusí být odrazivá, stačí jen, aby se od dopadajícího světla ohřívala pomaleji, než ta černá). Tedy tento mlýnek se otáčí opačným směrem, než ten předchozí.
Nyní k Vaší otázce, zda přístroj nemůže fungovat podobně jako Crookesův radiometr. Teoreticky vzato může. Postatný rozdíl zde bude ale ve velikosti těch efektů ve srovnání s přístrojem uvedeným v článku.
Myslím si, že cílem konstruktérů toho přístroje z článku nebylo udělat jednu stranu lopatek takovou, aby srážky kuliček s ní byly pokud možno absolutně nepružnými srážkami, při nichž se pohlcuje nejlépe celá kinetická energie dopadajících kuliček, zatímco na opačné straně lopatky by probíhaly srážky absolutně pružné. Takovéto provedení by vlastně bylo přesnou rekonstrukcí Nicholsova radiometru, a také by se ve stejném směru jako Nicholsův radiometr otáčelo. Nicméně z toho popisu jsem získal pocit, že to vroubkování tam bylo hlavně proto, aby se měnil průběh té srážky. Zatímco při odrazu od nekonečně tuhého povrchu se rotace dopadající kuličky po odrazu nemění, tak zde se díky modifikaci průběhu srážky měnil rotační stav kuličky.
Nicméně musím souhlasit, že pokud by pohlcování té energie vroubkovanou stranou lopatek mělo být podstatné, pak by zařízení teoreticky fungovalo i s kuličkami nulových rozměrů, tj. s hmotnými body. Myslím si ale, že přístroj z článku není takto postaven, a že ve skutečnosti jsou energetické ztráty na vroubkované straně lopatek velice malé. Každopádně pokud by přístroj z článku byl analogií Nicholsova radiometru, otáčel by se ve směru vroubkované strany lopatek, protože ta by díky nepružnosti srážek přijímala menší hybnost, než opačná strana nevroubkovaná (tj. vroubkovaná strana by hrála roli černé, a nevroubkovaná strana roli odrazivé plochy v Nicholsově radiometru).
Stejně tak přístroj z článku není analogií ani Crookesova radiometru. V Crookesově radiometru atomy té které strany lopatek předávají tepelnou, tedy neuspořádanou energii atomům vzduchu. To určitě není případ přístroje z článku. V Crookesově radiometru mají obě strany lopatek výrazně odlišnou teplotu, a právě tento teplotní rozdíl je motorem Crookesova radiometru. Naproti tomu teplotní rozdíl obou stran lopatek přístroje z článku je zanedbatelný, a už vůbec nebude hrát měřitelnou roli v ovlivňování pohybu lopatek, a to protože energie tohoto případného teplotního rozdílu je zanedbatelná ve srovnání s kinetickou energií kuliček.
Jinými slovy, zatímco rozdíl třeba třiceti stupňů Kelvina hraje nemalou roli při poměřování kinetické energie molekul, které jsou v tepelné rovnováze s odpovídající stranou lopatky (konkrétně při pokojové teplotě je rozdíl třiceti Kelvinů ekvivalentní rozdílu kinetické energie molekul zhruba 30/300=10% oproti kinetické energii molekul na chladnější straně lopatky), tak v případě makroskopických kuliček je příspěvek předané tepelné energie ke kinetické energii kuličky naprosto zanedbatelný.
Z toho potom plyne, že pokud se ty lopatky v přístroji z článku opravdu otáčí, tak vysvětlení není možno hledat v rozdílných tepelných ztrátách na opačných stranách lopatek. Ten rozdíl musí být akumulován z rezervoáru, který má podstatně větší energetickou kapacitu, než je energetický rozdíl odpovídající teplotnímu rozdílu lopatek, pokud tam vůbec nějaký měřitelný teplotní rozdíl vzniká. Tímto rezervoárem je právě rotace kuliček.
Opět musím konstatovat, že je to velice vtipně vymyšlený pokus. Je v něm spousta detailů, jejichž podstatnost si člověk uvědomí až při podrobném rozboru. Rozhodně to nevymysleli žádní hlupáci, a v žádném případě se nejedná o triviální pokus.
Tomáš Brauner,2010-06-17 19:46:31
Kloním se k názoru pana Kříže, že jde o mechanickou analogii Crookesova radiometru: od té změkčené strany lopatek se kuličky prostě odrážejí s menším impulsem než od strany tvrdé, stejně jako fotony dopadající na černou stranu lopatky radiometru. Nerozumím moc argumentu pana Brože, že podstatnou roli hraje rotace kuliček. (Nečetl jsem pozorně všechny Vaše příspěvky, proto se omlouvám, pokud je nějak dezinterpretuji.) Jak byste chtěl dosáhnout toho, aby se při odrazu od lopatky kuličky roztočily převážně jedním konkrétním směrem, takže jako celek by získaly nenulový moment hybnosti? Kromě toho mám za to, že díky svému malému rozměru by kuličky musely rotovat s příliš vysokou frekvencí, aby dokázaly kompenzovat moment hybnosti vrtulky.
Nahlédnutím do článku publikovaného ve Physical Review Letters (ke stažení zde: http://prl.aps.org/abstract/PRL/v104/i24/e248001) se dá snadno ověřit, že tam o rotaci kuliček není vůbec řeč, zato je zdůrazněno konvekční proudění v kuličkovém "plynu". To kompenzuje moment hybnosti předaný vrtulce; nejde tedy o moment hybnosti vlastní rotace kuliček, nýbrž jejich kolektivního pohybu vůči ose vrtulky.
Děkuji za odkaz plus asymetrické rotace kuliček
Pavel Brož,2010-06-18 00:43:09
Děkuji moc za odkaz na článek, bohužel můj účet na APS mi neumožňuje jeho stáhnutí, takže si budu muset jako obvykle počkat, až se objeví v Technické knihovně. Což jako obvykle bohužel nějaký ten pátek potrvá.
Říkáte konvekční proudění v kuličkovém plynu? Já jsem přesto přesvědčený, že tam ta souvislost s rotací kuliček bude, a nebude zanedbatelná. Neumím si představit, jak by se stejnému konvekčnímu proudění dalo zabránit, pokud by ty kuličky byly velikosti molekul - přesněji řečeno zabránit by se mu zmenšení kuliček na velikost molekul nedalo, a fungovat by to tedy mohlo pouze mimo termodynamickou rovnováhu, což ale vlastně ve zdejším přepisu článku zmíněno bylo.
Co se týče problému, jak by se předával kuličkám větší moment hybnosti v jednom než druhém směru, tak toto je dobře představitelné právě díky tomu měkkému odrazu, který trvá po nějakou krátkou dobu (každopádně déle, než trvá odraz tvrdý na druhé straně lopatky). Právě díky otáčení této konečné nenulové době odrazu se úhel lopatky během odrazu změní. Snadno tak zjistíte, že roztáčení kuliček v obou směrech nebude symetrické. Ze zákona zachování momentu hybnosti by pak plynulo, že úhrnný moment hybnosti kuliček by byl až na znaménko roven momentu hybnosti těch lopatek – samozřejmě za předpokladu, že by pohyb kuliček byl chaotický.
Pokud by zde mělo docházet ke konvekčnímu uspořádanému proudění, tak zde můžeme mít celkem tři rezervoáry momentu hybnosti – jedním bude hřídel s lopatkami, druhým již probíraný úhrnný moment hybnosti plynoucí z nesymetrické distribuce rotací kuliček v obou směrech, a třetím rezervoárem by bylo víření kuliček v celé krabici (podobně jako víření ping-pongových míčků v osudí s asymetricky umístěným fukarem). Nicméně toto víření (tedy onen konvekční pohyb onoho kuličkového plynu) by měl opět být zprostředkován právě přes onu nesymetrickou distribuci rotací kuliček.
Tzn. že v prvém kroku by měla být roztáčena hřídel s lopatkami díky nestejnému přenosu hybnosti z kuliček na obě strany lopatky – ano, uznávám, že toto je opravdu analogické s tím Nicholsovým (nikoliv Crookesovým) radiometrem, rozdíl je ten, že u Nicholsova radiometru dochází na černé straně lopatku k absolutně nepružnému odrazu (tj. k pohlcení), a moje výhrada v předchozím příspěvku trvá, zde nedochází k absolutně nepružnému odrazu – nicméně rozdíl v hybnosti zde je. Ve druhé kroku by mělo docházet k asymetrickému rozdělování rotací kuliček v obou směrech právě vzhledem k počínající rotaci těch lopatek. Konečně ve třetím kroku by pak mělo docházet právě díky té asymetrii rozdělení vzhledem ke směrům rotace ke vzniku vířivého konvekčního proudění po odrazech rozdílně rotujících kuliček od stěn nádoby.
V každém případě, ať už zde rotace kuliček hraje podstatnou roli, anebo se lze bez ní obejít tím, že se místo rotační energie kuliček jakožto jiný potřebný rezervoár vezme konvekční proudění, tj. asymetrické víření kuliček v nádobě (kuličky tedy finálně „obíhají“ v nádobě opačným směrem, než se točí hřídel), tak stále jde o netriviální experiment, který v žádném případě nemá nic společného s vodními mlýnky ani větrníky, jak jinde zaznělo. Snad se aspoň v tomto vláknu shodneme na tom, že tvar lopatek s tím nesouvisí :-)
Řekl bych...
Jan Kment,2010-06-16 12:37:25
...že ty kuličky vlivem gravitace a zároveň umístěním plošiny která je rozhýbává nejsou v prostoru zastoupeny rovnoměrně resp. náhodo/rovnoměrně, pravděpodobnost výskytu kuličky nad vrtulkou mi tak nějak připadá podstatně menší, protože hybná plošinka je posílá sice náhodně ale přece jen ze všeho nejvíc víceméně kolmo vzhůru: 45 - 90 stupňú, stoupání kuličky pod tupým úhlem se zdá vzácnější a také jsou takto vyslané kuličky vystaveny delšímu působení gravitace a tak se nad vrtulku hůře dostanou, tření vzduchu navíc zpomaluje padající kuličky, takže nějak nevím kde je rozdíl mezi klasickým větrníkem a tímto zařízením. Myslím že nějaká přípustná míra narušení konzistence náhodnosti by se jen těžko počítala, když náhoda je z principu nekonzistentní, ale rozhodně tu máme vážné determinanty, které ji narušují. Nebo se mýlím?
Také bych řekl
Petr Kr,2010-06-16 14:29:30
Mám stejný pocit, když jsem to viděl se točit, přemýšlel jsem proč a napadl mne klasický větrník. Vysvětlení pana Pavla Brože je sice velmi vědecké, ale mně se nezdá. Prostě, když dám naběračku do proudu vody jedním směrem, tak mi to utrhne ruku, a když ji obrátím, tak to udržím. Navíc ta vaše úvaha o vlivu potenciální energie kuliček nahoře mi také dává další argument a já ji tam vidím.
Tak, co jinak
Petr Kr,2010-06-16 14:40:40
Bude to fungovat po otočení o 90°? To je, když osa rotace toho stroje bude rovnoběžná s gravitační silou? Kuličky pak mohou být vystřelovány nahoru a vychylovány oběma směry rovnoměrně, aby dopadaly na ty lopatky a nebyly v rovnoběžném směru k nim. Prosím, požádejte někdo ty inženýry, aby to otočili a roztočili. Myslím, že jedno nebo druhé, ale obojí zároveň? To by byl jasný důkaz. Takto to opravdu není jednoznačné.
Hmm
Petr K,2010-06-16 16:30:58
Otocit to o 90 stupnu tak, aby osa byla svisle by skutecne bylo zajimave..
Nicmene nemuzu uplne souhlasit s Pavlem Brozem, ze kdyz (pro zjednodusseni) namirim dve trysky proti sobe, tak pomoci nich nic neroztocim. Nehodlam samozrejme zpochybnovat zakon zachovani hybnosti. Ale kdyz lopatku vytvaruji spravne (napr tvar lzice), tak ziskam z jednoho proudu vice hybnosti nez z druheho. Ten druhy vlastne nasmeruji jinam, vychylim. Je to teda samozrejme jen muj "dojem", na urovni machani naberackou ve vode, ale nejak nemuzu prijit na to, v cem je pripadne spatne.
Příměry s tekutinami nejsou plauzibilní
Pavel Brož,2010-06-16 22:56:39
Žádná z úvah používajících jako analogii proudění tekutiny (bez ohledu na to, jestli kapaliny, nebo plynu), ať už se jedná o větrník či lopatky ve tvaru naběraček atd., zde není aplikovatelná. Přístroj, resp. kuličky figurující v tomto experimentu nemá s kapalinou vůbec nic společného. Zde používané analogie s točením větrníku či proudění vody kolem lopatky tvaru naběračky totiž využívají základní vlastnost tekutin, a tou je obtékání. Chování tekutiny při obtékání překážek (opět jedno, zda je tou tekutinou kapalina nebo plyn), se diametrálně liší od srážek tuhých kuliček s těmito překážkami.
Pokud tomu nebudete chtít věřit, stačí zapřemýšlet nad hydrodynamickým anebo aerodynamickým paradoxem. Máte např. dvě vajíčka na velikém plochém podnose ve dřezu, a pustíte na ně pomalu úzký proud vody. Proud vody je sice nejprve odstrčí od sebe, aby je vzápětí opět přitáhnul k sobě. Nic takového nenapodobíte, když onen proud vody nahradíte např. řídce padajícím pískem!!! V případě řídce padajících zrnek písku budou vajíčka pouze odstrkována od sebe, nikdy ne přitahována.
V případě aerodynamické varianty tohoto paradoxu vezmete dva listy papíru, necháte je viset rovnoběžně k sobě směrem dolů, a shora dolů mezi ně lehce fouknete. Po krátkodobém vychýlení listů od sebe se tyto listy k sobě začnou při nepřetržitém foukání přibližovat. Ani zde nic podobného s pískem ani s kuličkami neuděláte!
Hydrodynamický i aerodynamický paradox jsou důsledkem platnosti Bernoulliho rovnice. Tuto rovnici lze např. pro kapaliny velice snadno odvodit např. ze zákona zachování energie. Bohužel je prakticky nemožné ji odvodit na základě mechanistických úvah o srážkách kuliček či jakýchkoliv pevných těles. Mimochodem, kdysi dávno jsem nad tím nějaké ty hodiny strávil, ale neúspěšně. Zašel jsem proto za svým kamarádem, který měl profesionální rozhled ve statistické mechanice, a ten mi sdělil, že je to obtížný nevyřešený problém, načež mě odkázal na množství odborné literatury a nemenší množství souvisejících, dodnes nevyřešených otázek.
Hydrodynamický a aerodynamický paradox (obecněji pak problematika obtékání v tekutinách) nejde vysvětlit na základě jednoduchých modelů srážejících se částic z toho důvodu, že v tekutině platí jisté implicitní předpoklady, které promítnuty do odpovídajících předpokladů u srážejících se kuliček vůbec nejsou triviální, natož pak intuitivní (matematicky formulováno – předpoklady, které jsou samozřejmými v mechanice tekutin, se ukážou být docela komplikovanými a naprosto nesamozřejmými okrajovými či vazebnými podmínkami v soustavě srážejících se kuliček). Jakákoliv tekutina proudící podzvukovou rychlostí (a pouze pro tento režim platí nejen např. uvedené paradoxy, ale také tak samozřejmé věci, jako že se v proudu tekutiny roztočí větrník – např. v proudu řídké plazmy urychlené na nadzvukovou rychlost by se netočil) má totiž chování určované všemi jejími částicemi, které se nacházejí v oblasti, jejíž přibližný průměr je dán vzdáleností, kterou urazí zvuk v této tekutině za dobu charakteristickou pro obtečení překážky.
Konkrétní příklad – vzduch obtékající rychlostí 1 metr za sekundu zhruba metrovou překážku. Chování molekul vzduchu v blízkosti překážky je během jejího obtečení (tj. za dobu cca 1 sekundy) ovlivněno nejen sousedními molekulami vzduchu, ale také molekulami vzduchu nacházejícími se v kouli o průměru cca 340 metrů – zvuková vlna totiž za onu sekundu potřebnou k obtečení překážky urazí právě tuto vzdálenost. Molekula obtékající překážku dá během jedné vteřiny obtékání o svém pohybu „vědět“ molekulám 340 metrů vzdáleným, a od molekul 170 metrů vzdálených dostane „feedback“, tj. reakci na svůj pohyb. Proto je obtékání v tekutinách nutno uvažovat jakožto principiálně kolektivní jev, který není možno redukovat na jednoduché mechanistické úvahy nad srážkami kuliček.
A přesně totéž platí samozřejmě i obráceně – totiž že pohyb kuliček srážejících se v onom přístroji NELZE v žádném případě posuzovat na základě analogií s točením větrníků či otáčením se naběračkových lopatek v proudu tekutiny.
Mimochodem, ten můj příměr s těmi tryskami nebyl míněn jakožto model použitelný ad absurdum včetně všech mikrodetailů, jako je obtékání lopatek proudy z trysky. Natož pak jejich ohýbání v gravitačním poli. Chtěl jsem jím jen argumentovat proti nekorektnímu použití analogie s vodním kolem na přístroj uvedený v článku, konkrétně jsem chtěl poukázat na fakt, že ve vodním kolu je hnacím médiem uspořádaný tok kapaliny v protikladu k neuspořádanému pohybu kuliček v přístroji. Kdybych věděl, že můj příměr bude použit až do takových detailů, vylepšil bych ho minimálně tím způsobem, že trysky by stříkaly všemi směry obrovskou rychlostí jednotlivé kapičky, které by se díky své rychlosti odrážely od lopatek. Zkrátka bych to doplnil o podmínku neplatnosti Bernoulliho rovnice.
Příměry s tekutinami?
Petr Kr,2010-06-17 09:15:47
Nejprve jsou na to vyvrácení našich "bludů" dobré, když to zpochybňujeme, tak zase nejsou dobré. Já si myslím, že když kuličky písku sypu do naběračky, tak to má jiné dopady než když kuličky písku sypu na obrácenou naběračku. A snad i pan Kment a další to vidí podobně. Prostě ty naběračky umístěte v gravitačním poli neutrálně, tj. otočte to o 90° a jste z obliga. Nemusíte potom vyvíjet složitou teorii zanedbávaje selský rozum. Provést něco nesymetricky a potom říct, že ta nesymetrie na to nemá vliv se mi zdá nevědecké.
Natřete lopatky z jedné strany stříbrnou barvou, z druhé černou, umístěte to tak, aby na to svítilo slunce a divte se, že se to točí ve vakuu. Potom na to aplikujte teorii mechanické fyziky a zanedbejte gravitaci. Zase se to bude dát zdůvodnit?
Netvrdím, že mám stoprocentně pravdu, ale něco mi tam nehraje, co mi brání to nezpochybňovat. Odstraňte mé pochyby s využitím nesymetrií a pak to předveďte.
Základní neporozumění
Pavel Brož,2010-06-17 12:23:56
Podívejte se, velice jednoduchý protipříklad k vašemu tvrzení - pokud by měl mít na funkci přístroje vliv tvar lopatek ve tvaru naběraček, tak by bylo možné v principu čerpat energii např. z tepelného pohybu molekul vzduchu. Postavil by se mlýnek s lopatkami ve tvaru naběraček, a nechal by se jen tak stát ve vzduchu v nějaké místnosti, kde by nefoukalo. Gravitační pole tam máme, kinetická energie molekul spolu s narůstající výškou v tom gravitačním poli klesá podle úplně stejného zákona, jako klesá kinetická energie těch kuliček v tom přístroji, takže jediným podstatným rozdílem je to, že v případě toho přístroje jsou ty kuličky podstatně větší, než jsou molekuly vzduchu.
Podle Vás by se to mělo zřejmě točit. Ale ono by se to netočilo. Bylo by to v rozporu s druhou termodynamickou větou.
Pokud byste se maličko orientoval ve fyzikální literatuře, pak byste věděl, že na popisy podobných možných obelstění termodynamické věty byly sepsány za více než sto let tuny článků. Triviality typu tvary lopatek atd. byly vyřešeny nejdříve, ukázalo se, že pro seberafinovaněji tvarované lopatky neexistuje způsob, jak jakýkoliv takový mlýnek tepelným pohybem dopadajících částic roztočit. Vymýšlely se všemožné rafinovanější mechanismy, ono zmiňovaná Feynmanova rohatka se západkou je pouze jeden z mnoha speciálních případů zařízení, které by měly být schopné převádět dokonale neuspořádaný pohyb na pohyb uspořádaný. Výsledkem všech těchto tun článků byl závěr, že je to nemožné.
Tyto závěry samozřejmě platí i pro tento přístroj. To, že se přístroj točí, není způsobeno tím, že se podařilo vymyslet tvar lopatek takový, který by konečně uměl čerpat tu energii z dokonale neuspořádaného pohybu (což je např. pohyb molekul systému, který je v tepelné rovnováze). To že se to točí je způsobeno tím, že systém v termodynamické rovnováze není. Což nakonec říkají i sami autoři experimentu. Tvar lopatek zde není tím faktorem, který ovlivňuje otáčení hřídele přístroje. Tím faktorem je kvalita povrchu těch lopatek, která způsobuje jiný průběh srážky na obou stranách lopatky, a tím pádem přenos translační kinetické energie kuliček do jejich kinetické energie rotační. Toto je to jádro pudla.
Pokud by byly lopatky vytlačeny do podoby naběraček, přístroj by se otáčel stále stejným směrem určeným tím drsným povrchem, nikoliv směrem určeným vydutím té lopatky.
Lituji, ale je to opravdu o znalosti té literatury, není v mých silách zreprodukovat zde v několika větách výsledky analýz řady špičkových vědců za sto let bádání. Pokud tomu nevěříte, že tvar lopatek s tím nemá nic společného, tak je to smůla, opravdu neexistuje žádná královská cesta, jak vás tady přesvědčit.
Neporozumnění u koho?
Petr Kr,2010-06-17 13:25:30
Pane Brož, vy mi tu zase říkáte nějaký specifický ideální případ, který možná myslíte, že nechápu. Prostě to opravdu nebude fungovat bez kuliček jen tak v plynu. Podle mne se to točit nebude. To my podsouváte chybný výrok, který jsem já opravdu, ale opravdu neřekl. A vzápětí říkáte, že to, že se to točí je dáno specifickým povrchem lopatek. Takže si dle mne neodporujeme. Rozdíl je jen v tom, že někdo to interpretuje jen jednou silou a někdo jich tam vidí více a neumí rozlišit jejich absolutní hodnotu (to, která je opravdu dominantní).
Není ten pokus náhodou špatně?
Marek Vítek,2010-06-14 14:10:26
Mám dojem, že ten pokus by vůbec nefungoval, pokud by byl symetrický, tj. osa mlýnku vertikálně a třepací desky dvě. Takhle se kuličky při pádu z vrchu udrží na lopatkách s vroubky o něco déle (je jich tam v daném č.rozmezí víc) a pak se nejedná o model odběru tepelné energie (výroba mech. energie ochlazováním, bez tepelného spádu), ale o využívání potenciální energie kuliček v tíhovém poli.
tak nejak
Petr K,2010-06-15 10:29:50
Taky musim rict, ze mi ten pokus pripadne az skoro banalni. "specialni" povrch zpusobi lepsi predani energie srazky anebo delsi pobyt kulicky na lopatce (ci samozrejme kombinaci obojiho). Tak ci onak jde o prenos kineticke a potencialni energie z telesa na teleso. Skoro se mi chce rici "no a?". Myslim ze podobny vysledek by sel ziskat i tvarem lopatek napr. do V. tj. v jednom smeru by krome srazky lopatky i kulicky nabiraly, podobne jako vodni mlyn.
Vůbec to není špatně
Pavel Brož,2010-06-15 23:24:43
Gravitační pole zde vůbec nemusíte uvažovat, resp. nemusíte ho uvažovat minimálně za předpokladu, že tloušťka těch lopatek je zanedbatelná. Srovnání s vodou ve mlýně není na místě, protože voda na to kolo padá seshora, nestříká rovnoměrně ze všech směrů. Pokud byste opravdu realizoval místo padající vody veliké množství trysek orientovaných v náhodných směrech, ale tak, aby ke každé trysce existovala stejně orientovaná opačná se stejnou rychlostí vody v místě křížení paprsků, tak se vám žádné kolo, byť seberafinovaněji tvarované, točit nebude. Bylo by to totiž v rozporu se zákonem zachování hybnosti a momentu hybnosti.
Je důležité si uvědomit, že bez ohledu na přítomnost gravitačního pole je rychlost každé kuličky v absolutní hodnotě stejně veliká při pohybu nahoru i dolů. Zanedbáte-li tloušťku lopatky, tak to v důsledku znamená, že hybnost předávaná kuličkami lopatce je stejná, ať už na ni dopadají shora, nebo zdola. V konečném důsledku se lopatky nemohou pohybovat, a to bez ohledu na jejich tvar (tj. ani tvar naběračky či véčka by nepomohl).
Fígl, že se to točí, je skryt v detailu. Kuličky mají svůj konečný nenulový rozměr a mohou přebírat kromě hybnosti i rotaci, tj. moment hybnosti. A točí se to proto, že systém jako celek ve skutečnosti NENÍ v termodynamické rovnováze, a trvalo by velice dlouho, než by se do ní dostal (za předpokladu, že by byl tepelně izolovaný od okolí). Není v ní mj. proto, že na začátku pokusu mají kuličky nulovou rotaci, tj. i moment hybnosti, tj. energie není rovnoměrně distribuována mezi všechny dostupné stupně volnosti.
Dále, a to je mnohem podstatnější, skutečná termodynamická rovnováha by nastala teprve tehdy, kdyby tepelná energie produkovaná srážkami zůstávala uvězněná v systému, tj. neztrácela by se ze systému pryč. Pak by se nakonec dostaly do stavu tepelné rovnováhy i atomy kuliček a lopatek, jenže v tom okamžiku by přestal fungovat ten efekt vroubkované strany lopatky, který způsobuje větší roztáčení dopadajících kuliček. Diskuze, proč by tomu tak bylo, je stejná, jako v případě rohatky se západkou. Po dosažení skutečné termodynamické rovnováhy by totiž nebyl žádný důvod, aby se preferoval tok energie do nějakého vybraného stupně volnosti (zde tedy do rotační energie kuliček), to by pak totiž už opravdu bylo ve sporu s druhým termodynamickým zákonem. Perpetuum mobile druhého druhu - totiž stroj měnící neuspořádanou tepelnou energii na uspořádanou mechanickou - totiž ve své podstatě není ničím jiným, než preferovaným tokem energie do nějaké preferované podmnožiny vybraných stupňů volnosti (kterým může být např. ono otáčení hřídele).
Ve skutečnosti sami autoři uvádějí, že jejich stroj NENÍ perpetuum mobile druhého druhu, ale svého druhu Carnotův stroj. Carnotův stroj může fungovat právě proto, že jako celek NENÍ v termodynamické rovnováze - část stroje se zahřívá např. přitápěním pod kotlem, jiná část stroje se ochlazuje, např. výměnou tepla s tepelným výměníkem (lidově řečeno s chladičem). Tepelná energie ve stroji jako celku není uvězněna, ztrácí se z něj (resp. při plynulém provozu jím protéká směrem od topeniště pod kotlem do okolí). A stejně totéž se děje i v přístroji zkonstruovaném autory.
Takže opravdu, nenechme se mýlit - není to v žádném případě samozřejmý pokus, a jak vidno z reakcí, je velice snadné jej pochopit chybně. Není to ani pokus vyvracející kterýkoliv ze známých fyzikálních zákonů, včetně termodynamických. To ale nic neubírá na tom, že je vtipně vymyšlený. Navíc vzhledem k tomu, jak je nenáročný, tak mohl být vlastně klidně udělán možná už před sto lety. Kdyby se tak bývalo stalo, tak by Feynman příslušnou pasáž o rohatce a západce v jeho proslulých přednáškách z fyziky dost možná doplnil o neméně zajímavý rozbor fungování právě tohoto stroje. Osobně si myslím, že by si to nenechal ujít :-)
Možnou existenci Maxwellova démona
Frantisek Kriz,2010-06-14 13:30:24
v biologii kdysi vypočítal prof. Čápek
http://pre.aps.org/abstract/PRE/v57/i4/p3846_1
Hledal biology pro potvrzení a už je nestihnul najít
Je to přesně tak, jak říkáte
Pavel Brož,2010-06-14 23:44:01
Shodou okolností jezdívám vlakem s mým spolužákem z vysoké školy, svého času doktorandem u prof. Čápka, mnohokrát mi jeho dosti převratné výsledky popisoval. Je veliká škoda, že prof. Čápek tak předčasně odešel, jeho výzkum byl velice zajímavý.
Roman Rodak,2010-06-14 13:18:15
tak ja mam aj par otazok k samotnemu obsahu clanku:
1, moze povodny feynmannov stroj fungovat ak by sme v komore T2 predpokladali dokonale utesnenie (energia medzi komorami by sa nemusela odovzdavat mechanicky) a nizsi tlak ako v T1, idealne vakuum? sice si neviem predstavit ako by sa ten stroj mohol sam od seba roztocit, ale tiez uz asi pol hodinu neviem dojst na ziadny protiargument...
2, podla popisu tohoto moderneho holandskeho stroja nevidim ziadne porusenie 2. zakona - ked si modre gulicky predstavim ako molekuly plynu a spodnu vibrujucu dosku ako cast povrchu nejakeho pevneho objektu a pohyb tejto dosky ako vysledok tepelneho pohybu jednotlivych atomov tohoto pevneho objektu, tak mi vychadza, ze modra gulicka narazom do rotora sice strati cast energie, ale tuto energiu si o chvilu doplni zrazkami s inymi gulickami, ktorym spodna vibrujuca doska zabezpecuje konstantnu strednu rychlost. Zmensene bilion krat, vibrujuca doska je ako keby teleso s konstantnou teplotou, ktore je v priamom styku s plynom, plyn sa jemne ochladzuje lebo odovzdava energiu rotoru a tym padom vznika teplotny gradient medzi rotorom a pevnym telesom.
Roman Rodak,2010-06-14 13:19:41
aha, tak este doplnenie k bodu 1 - tym ze by tam bolo vakuum, odpadlo by obcasne zlyhanie zapadky a teda ozubene koleso by sa mohlo tocit len povodne zamyslanym jednym smerom
Myslím, že to je jinak
Pavel A1,2010-06-14 23:36:18
Jestli dobře chápu ten Feynmanův argument, tak jde o to, že pokud by ta západka a to ozubené kolo měly být tak jemné, že posun o jeden zub vyvolá tepelná fluktuace v levé nádobě, tak ta západka sama by se vlastními tepelnými fluktuacemi pohybovala více, než je výška zubu, a proto to nemůže fungovat. Jestli je v té nádobě vakuum s tímto argumentem nijak nesouvisí.
Nic proti článku samotnému
Ondřej Vévoda,2010-06-14 12:46:54
Článek samotný je zajímavý, proti jeho obsahu nic nemám. Jde mi jen o tu zbytečnou bulvarizaci v nadpisu. Chápu proč to ta pracoviště dělají, ale moc nechápu, proč se to objevuje i tady. Toť vše...
Nevidím na tom nic špatného
Pavel Brož,2010-06-14 12:36:29
Jednak na tom pracovišti udělali pokus, který se nejvíce přiblížil oné známé Feynmanově rohatce se západkou. Musím říct, že to, že se to zařízení opravdu otáčí, je samo o sobě dosti šokující věc pro každého teoretického fyzika, a objasnění důvodů, proč tomu tak je a že ve skutečnosti nejde o popření druhého termodynamického zákona, nic nemění na tom, že ten pokus je udělán docela důmyslně.
Další věcí je to, co bylo také zmíněno ve článku, totiž možné lepší pochopení mikrobiologických motorů. Mimochodem v otázce, nakolik jsou či nejsou mikroorganismy či některé jejich struktury realizací Maxwellova démona, zdaleka jasno není. A dokonce ani otázka principiální možné existence či neexistence Maxwellova démona dodnes není definitivně uzavřena, ač je to problém půldruha století staré. Před pár lety na to téma vyšel velice pěkný přehledový článek v českých PMFA, kde se sumarizovaly různé přístupy za celou historii finálně neúspěšných pokusů o exaktní důkaz neexistence Maxwellova démona. Ačkoliv se měnily přístupy (např. z mechanistického na informační, atd.) a stejně tak i metody (studium problémů na kvantové úrovni, optické pinzety, atd.), tak definitivně tento problém stále uzavřený není. Nicméně každý další příspěvek včetně toho zmíněného v článku přispívá k lepšímu pochopení těchto dějů.
Úplně nakonec pak lze pouvažovat nad údajnou amorálností "samoreklamy" oněch pracovišť, kde používají pro média chytlavé nadsázky pro pojmenování svých objevů místo sterilně znějících striktně vědecky korektních formulací. Inu, to je věc marketingu ve vědě. Dobře dělaný marketing přináší peníze, a to i do vědy. Stačí se pak kouknout, kolik jich přináší na západ od našich hranic a kolik u nás, úsudek už si každý udělá sám.
presne tak
Michal Kvasnicka,2010-06-14 11:35:10
Nelze nez slouhlasit s nazorem Ondreje Vevody. take nechapu proc se clanek tohoto typu na tomto, jinak velice serioznim, portalu vlastne objevil. Vysvetlujici poznamka na konci textu je sice dulezita, ale clanek jako celek je zavadejici.
Nadpis článku
Ondřej Vévoda,2010-06-14 10:30:26
S poznámkou pod článkem se nedá než souhlasit, nicméně mi v tom případě není jasné, proč se podobné chování pracovišť podporuje. Tento server a jeho články mi přijdou velice kvalitní, ale přebírání nadpisů (nebo celých článků?) v duchu bulváru ho poněkud degraduje. Pokud nikdo Feynmana nepřechytračil, proč je to použito v názvu článku? I já jsem klikl na odkaz abych se dozvěděl v čem se tento geniální fyzik mýlil a ono ejhle...
Nadpis článku
Ondřej Vévoda,2010-06-14 10:30:26
S poznámkou pod článkem se nedá než souhlasit, nicméně mi v tom případě není jasné, proč se podobné chování pracovišť podporuje. Tento server a jeho články mi přijdou velice kvalitní, ale přebírání nadpisů (nebo celých článků?) v duchu bulváru ho poněkud degraduje. Pokud nikdo Feynmana nepřechytračil, proč je to použito v názvu článku? I já jsem klikl na odkaz abych se dozvěděl v čem se tento geniální fyzik mýlil a ono ejhle...
Možná
Josef Pazdera,2010-06-14 12:45:05
Ano, máte pravdu i nemáte. Na název článku je možné se dívat z mnoha pohledů. Jeden je, že by již z názvu mělo být zcela jasné, o co v článku jde. Myslím si ale, že u populárního článku už to tak být nemusí. Jsou weby, které si tu a tam jistou dávku nadsázky dovolují a počítají s tím, že čtenář je do jisté míry v obraze a nebo se do něj přečtením celého článku dostane. Mezi takové patří například i Science News. Jde o stránky, o kterých říci, že dělají bulvár by nebylo moudré. Také zde najdete článek s názvem, který v originále zní: „Bouncing beads outwit Feynman“. Ve chvíli, kdy reaguji na tuto výtku přečetlo článek v Science News již zhruba o dva řády čtenářů více a nikdo se v diskusi nad názvem nepozastavuje. Pokud zavádějící název někoho donutil číst článek až dokonce a jinak (kdyby hned bylo jasné vo co go) by to neudělal, omlouvám se.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce




