První část cyklu článků o neutrinech byla věnována jejich objevu, základním vlastnostem a snahou o určení jejich hmotnosti, v druhé části  jsme se věnovali jejich produkci a v třetí části  pak detekci. V poslední části se zaměříme na jednu z jejích nejzajímavějších vlastností - na oscilace neutrin.

Oscilace neutrin jsou jevem, při kterém dochází k přeměně jednoho typu neutrina na jiný. Souvisí s jednou z nejpodivuhodnější kvantových vlastností, které se v mikrosvětě objevují. Jednotlivé typy neutrin odlišujeme podle toho, z kterých typem neutrin nabitých leptonů vznikají, nebo který nabitý lepton vzniká při jejich interakci. Pokud by oscilace neutrin neexistovaly, vznikalo by společně s elektronem elektronové antineutrino (s pozitronem elektronové neutrino) a při interakci takto vzniklého antineutrina (neutrina) spojené se vznikem nabitého leptonu by musel opět vzniknout elektron (pozitron). Stejně tak by neutrino vzniklé společně s mionem muselo v takových reakcích produkovat mion a to, které vzniklo společně s tauonem by muselo v interakci produkovat opět tauon. Pokud existují oscilace neutrin, tak se může neutrino, které vzniklo jako elektronové, chovat při detekci (interakci) jako mionové či tauonové. Takový proces pozorujeme i u jiných částic. Připomeňme si proces oscilací neutrálních mezonů K, o kterém jsme na Oslovi psali poměrně nedávno. První úvahy o možnosti takového jevu u neutrin se objevily v roce 1957 v pracích Bruna Pontecorva. Jev může nastat jedině v případě, že se klidové hmotnosti jednotlivých neutrin liší. V době, kdy se spíše předpokládalo, že je klidová hmotnost neutrin nulová, se o existenci jejich oscilací příliš neuvažovalo. S experimentálními náznaky existence oscilací neutrin tak byla nastolena i otázka jejich nenulové klidové hmotnosti.

Zvětšit obrázek

Experiment s oscilacemi neutronů se připravuje i pro reaktory Daya Bay v Číně

Neutrina, která pozorujeme (elektronové, mionové a tauonové) jsou směsí jiných tří částic. Nazvěme je neutrino jedna, dvě a tři. Námi pozorované elektronové neutrino tak nebude čistým stavem, ale bude směsí neutrin typu jedna, dvě i tři. A tak tomu bude i u ostatních neutrin. Přitom neplatí přesně, že elektronové neutrino bude mít nejblíže k prvnímu typu (bude obsahovat jeho největší část - příměs), druhý typ pak bude nejvíce obsažen v mionovém neutrinu a třetí v tauonovém. Jak si za chvíli ukážeme, je z experimentu jasné, že míchání některých neutrin je velmi intenzivní a v námi pozorovaných neutrinech je srovnatelným způsobem zastoupeno více stavů. Něco takového v našem světě „normálních“ rozměrů nepozorujeme. Nestává se, že by daný konkrétní člověk byl směsí tří jiných a jednou bychom jej pozorovali jako daného známého a podruhé jako někoho jiného. I když nám to občas může u někoho tak připadat :-)

Stejně jako v případě míchání způsobujícího oscilace neutrálního mezonu K, které jsme popisovali ve zmíněném článku, lze použít i pro popis oscilací neutrin matici 3x3. U neutrálních mezonů K se míchaly tři typy kvarků, u neutrin se míchají tři typy neutrin.

V případě kvarků to byla matice Cabibbo-Kobayashi-Maskawa, v případě neutrin se tato matice někdy označuje jako matice Pontecorvo–Maki–Nakagawa–Sakata. V obecném případě potřebujeme pro popis průběhu oscilací neutrin a jednotlivých prvků matice pět nezávislých parametrů. Dva představují rozdíly kvadrátů hmotností jednotlivých typů neutrin a tři parametry, které popisují jejich míchání: jeden míchání mezi prvním a druhým typem, druhý míchání mezi prvním a třetím typem a třetí míchání mezi druhým a třetím typem neutrin. Tyto parametry se často vyjadřuji ve formě tzv. směšovacích úhlů (ještě přesněji jako kvadráty jejich sinů). Hodnoty těchto parametrů také můžeme měřením oscilací různých neutrin určit. Nelze však z oscilací určit absolutní hodnotu velikosti hmotnosti jednotlivých typů neutrin.

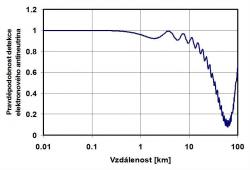
Pravděpodobnost, že neutrino, které vzniklo například jako elektronové, bude jako elektronové i pozorováno, se vlivem oscilací mění se vzdáleností detektoru od zdroje. Průběh oscilací závisí také na energii neutrin. Parametrem, který popisuje průběh oscilací neutrin s různou energií je pak vzdálenost dělená energií neutrina. V případě, že oscilační délka je malá vůči velikosti zdroje, který neutrina vyzařuje, nebudeme pozorovat změny pravděpodobnosti se změnou vzdálenosti od zdroje. Navíc může být průběh oscilací ovlivněn i prostředím, kterým se neutrina pohybují. Například rozměr nitra Slunce je větší než oscilační délka pro oscilace elektronových neutrin a navíc je v plazmatu Slunce velmi vysoká hustota elektronů. Na Zemi tak pozorujeme jen výsledný deficit elektronových neutrin a ne oscilace jejich počtu se vzdáleností. Velikost tohoto deficitu se mění s hodnotou energie neutrin.

Oscilace slunečních neutrin

Experimentální objev oscilací neutrin je spojen se snahou pozorovat neutrina přilétající ze Slunce. Podrobná historie prvního zachycení a následného pozorování těchto neutrin byla popsána v druhé části. Připomeňme si, že již v roce 1967 pozoroval Raymond Davis Jr. neutrina přicházející ze Slunce. Zjistil, že na Zemi dopadá pouze zhruba jedna třetina předpokládaného toku elektronových neutrin. Raymond Davis postupně vylepšoval svůj detekční systém postavený na chloru a analyzoval všechny zdroje možných nepřesností. Zároveň John Bahcall analyzoval a zpřesňoval modely Slunce, které předpovídaly jeho neutrinovou produkci. V sedmdesátých a osmdesátých letech se tak postupně ukazovalo, že chybějící elektronová neutrina ze Slunce jsou realitou. A kandidátem na jejich vysvětlení se stal právě jev oscilací neutrin. To se s konečnou platností potvrdilo na počátku tohoto tisíciletí, kdy byl dokončen detektor SNO, který umožňoval detekovat všechny typy neutrin. Zjistil, že elektronových neutrin je zmíněná zhruba třetina a všech neutrin dohromady přichází na Zemi právě tolik, kolik se má na Slunci produkovat v termojaderných reakcích elektronových neutrin. Od té doby se stále přesněji měří poměr mezi tokem elektronových a všech neutrin ze Slunce na Zemi pro různé oblasti energií slunečních neutrin. Připomeňme, že energie slunečních neutrin je v řádu zlomku, jednotek až desítky MeV. A velikost měřeného deficitu elektronových neutrin se pro různé jejich energie liší.

V tomto případě studujeme hlavně oscilace (přeměny) mezi prvním typem neutrin a druhým. Jak už bylo zmíněno, charakteristická délka na které zmíněné oscilace probíhají je menší než je rozměr nitra Slunce, dochází k termojaderným reakcím. Navíc je zde velmi vysoká hustota elektronů. Průběh oscilací se tak eliminuje a na Zemi pak pozorujeme jen celkový úbytek elektronových neutrin ve prospěch jiných typů. Zmíněný proces se označuje Micheevův-Smirnovův-Wolfensteinův efekt a pomocí něho můžeme vysvětlit pozorování detektorů slunečních neutrin v různých oblastech jejich energií.

Zvětšit obrázek

Zobrazení pravděpodobnosti, že antineutrino z reaktoru dorazí do daného místa v podobě elektronového antineutrina, v závislosti na vzdálenosti místa od reaktoru. Čárkovaná čára je předpověď bez oscilací, tečkovaná čára a šedá zóna pak ukazuje předpověď s využitím parametrů získaných z oscilací slunečních neutrin. Zobrazeny jsou experimenty s detektory u různých reaktorů (zdroj KamLAND).

 

Oscilace reaktorových neutrin

Víme, že velké množství antineutrin se produkuje v reaktorech. Je tak možno studovat, jakým způsobem probíhají jejich oscilace na jiné typy v závislosti na vzdálenosti od reaktoru. V tomto případě je typická energie zase v řádech keV a MeV. Jedná se tedy o energie v oblasti zhruba stejné jako u slunečních neutrin. Jde zase o elektronový typ, ovšem v tomto případě o zmíněná antineutrina. Ta ovšem mají stejné charakteristiky míchání s ostatními antineutriny jako neutrina elektronová s dalšími typy neutrin. Oscilační délka je tak stejně krátká a při předpovědích, jak bude oscilace reaktorových neutrin vypadat, bylo možné částečně vycházet s výsledků získaných u neutrin slunečních. Výhodou je, že můžeme získávat data pro různé vzdálenosti od reaktoru a sledovat průběh oscilací na této vzdálenosti. Mohly by se tak odlišit a zkoumat oscilace mezi prvním a druhým typem neutrina i mezi prvním a třetím. Právě pro menší vzdálenosti by se mělo projevit i míchání s jinými typy neutrin. Byla provedena řada experimentů, ve kterých byly detektory umístěny ve vzdálenostech desítek až stovky metrů.

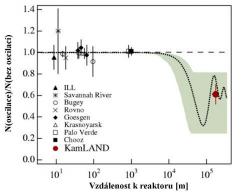
Důležitým krokem k upřesnění míchání různých typů neutrin bylo studium oscilací reaktorových antineutrin experimentem CHOOZ, který proběhl ve Francii. Využívaly se dva tlakovodní reaktory, od kterých byl detektor vzdálen zhruba 1000 m. Zhruba o dvě stě metrů blíže reaktoru byl detektor v případě experimentu, který využíval reaktory v Palo Verde (Arizona v USA). Oba tyto experimenty žádné oscilace nepozorovaly, což prokázalo, že míchání mezi prvním a třetím typem neutrina je velmi malé (směšovací úhel a tedy i kvadrát jeho sinu je velmi malý).

V této vzdálenosti zhruba dvou kilometrů by mělo být pozorováno první oscilační maximum těchto oscilací. Ovšem velikost tohoto prvního maxima v oscilacích není větší než deset procent. Přesnost měření experimentu CHOOZ a neutrinového experimentu v Palo Verde tak neumožnila tyto oscilace pozorovat. A jak už bylo zmíněno, oba experimenty také oscilace nezaznamenaly. V současnosti se připravuje několik pokročilejších experimentů. Jedním z nich je čínský, který bude využívat tři reaktory v jaderné elektrárně Daya Bay nedaleko Hongkongu. Po spuštění posledního z nich v tomto roce budou mít celkový tepelný výkon 17 GW. Daya Bay se tak zařadí k pěti nejvýkonnějším jaderným elektrárnám na světě. Detektory budou také větší než v předchozích experimentech a budou umístěny jak blízko reaktorů, tak i ve vzdálenosti necelých dvou kilometrů. Ty blízké by neměly vidět žádné oscilace a srovnání jejich měření s měřeními vzdálených detektorů by mělo snížit možné systematické nejistoty v měření toku neutrin. Pro snížení radioaktivního pozadí budou také detektory umístěny hlouběji v podzemí. Přesnost měření velikosti míchání mezi prvním a třetím typem neutrina by se tak měla zvýšit o více než řád.

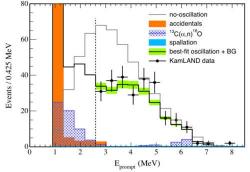
Už v dřívějších částech cyklu o neutrinech byl zmiňován japonský detektor KamLAND, který využívá kapalný scintilátor. Pomocí něho se studovaly oscilace antineutrin vznikajících v japonských jaderných reaktorech. V tomto případě byla efektivní vzdálenost detektoru od reaktorů v řádu stovek kilometrů. V této oblasti, už se projeví velmi silně oscilace způsobené mícháním neutrin prvního a druhého typu. Velikost těchto oscilací určuje i oscilace slunečních neutrin a můžeme ji pomocí nich předpovědět. Jak je vidět na obrázku, je velikost změřených oscilací antineutrin z japonských reaktorů v dobré shodě s předpovědí, která byla získána pomocí pozorování oscilací neutrin slunečních. Výhodou experimentu KamLAND bylo i to, že dokázal určovat energii neutrin. Průběh energetického spektra je citlivý k parametrům oscilací. Kombinace měření detektoru KamLAND a experimentů z detekcí slunečních neutrin tak umožnila určit relativně přesně rozdíl kvadrátů hmotností prvního a druhého typu neutrina a velikost jejich míchání.

Zvětšit obrázek

Energetické spektrum antineutrin detekovaných detektorem KamLAND. Je vidět, že toto spektrum lze vysvětlit pouze s využitím oscilací (zdroj KamLAND).

 

Oscilace neutrin ze sekundární složky kosmického záření

Jak jsme už podrobněji na Oslovi rozebírali v článku o kosmickém záření a druhé části tohoto seriálu o neutrinech, vznikají interakcí primárních částic kosmického záření v atmosféře mezony pí. Ty tak jsou významnou součástí sekundární složky kosmického záření. Při rozpadu nabitých mezonů pí vznikají miony a mionová neutrina (antineutrina). Miony se rozpadají na elektron či pozitron a dvě neutrina (správněji jedno neutrino a jedno antineutrino). Jedno z nich je mionové a druhé elektronové. V každém takovém rozpadu mezonu pí tak v konečném důsledku vznikají dvě neutrina mionová a jedno elektronové. V sekundární složce kosmického záření tak máme směs mionových neutrin (antineutrin) a elektronových neutrin (antineutrin) přesně dánu a zhruba v poměru 2:1. Můžeme tak porovnávat, jaký je poměr mionových a elektronových neutrin z kosmického záření, která dorazila do detektoru z různých míst v atmosféře. Například z atmosféry, která je nad povrchem, který je na protilehlé straně zeměkoule, než je detektor.

Energie atmosférických neutrin se pohybuje v širokém rozmezí od zlomků GeV až po hodnoty větší než 100 GeV. Pokud je budeme detekovat z různých směrů, tak před zachycením v detektoru uletí dráhu od desítek až po třináct tisíc kilometrů (ty, které letí z opačné strany zeměkoule). Mohly se tak studovat změny počtu mionových neutrin se vzdáleností detektoru od místa jejich vzniku. Protože se energie atmosférických neutrin mění ve velmi širokém rozmezí, je rozumné vyjádřit průběh oscilací v závislosti na podílu vzdálenosti detektoru a energie neutrina.

Jak bylo popsáno v předchozí části, pozorujeme v případě slunečních neutrin pouze deficit těchto neutrin. V případě neutrin z interakce kosmického záření v atmosféře pozorujeme skutečně pokles mionových neutrin a jejich opětnou regeneraci v závislosti na vzdálenosti detektoru neutrin od zdroje, tedy opravdové oscilace. Měření kosmických neutrin tak bylo první, které opravdu přímo potvrdilo existenci těchto oscilací. Byl totiž pozorován nejen úbytek jednoho typu neutrin při vzdalování detektoru od zdroje, ale i opětný nárůst jejich počtu ještě ve větší vzdálenosti.

Zvětšit obrázek

Poměr počtu pozorovaných neutrin a těch, které by byly pozorovány bez oscilací, v závislosti na poměru vzdálenosti L detektoru od zdroje a energii neutrina získaný detektorem KamLAND (zdroj Československý časopis pro fyziku).

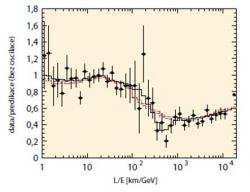
Experimenty využívající první generaci velkých neutrinových detektorů, jako byl IMB, MACRO a Kamiokande II, pozorovaly první indicie oscilací atmosférických neutrin. Jednalo se o deficit mionových neutrin. Pokročilejší detektory Soudan 2 a SuperKamiokande pak studovaly zmíněnou závislost pravděpodobnosti zachycení mionových neutrin na vzdálenosti. Detektor Soudan 2 je složen z 960 t železa a SuperKamiokande pak 50 000 t čisté vody. Měření těchto detektorů ukázala, že v tomto případě je určený rozdíl kvadrátů hmotností dvou stavů rozdílný než u neutrin slunečních a mionové neutrino se tak nemění na elektronové ale na jiné. Stalo se tak jasným, že nejméně dvě neutrina mají nenulovou hmotnost. Zároveň se také podařilo zjistit další ze směšovacích úhlů. Tento úhel byl dost velký, takže bylo jasné, že se druhý a třetí typ neutrina se také míchají velmi silně.

Zvětšit obrázek

Urychlovač J-Parc začíná produkovat svazek mionových neutrin pro experiment T2K (zdroj T2K).

 

Oscilace neutrin produkovaných urychlovačem

Velmi důležitým nástrojem studia oscilací neutrin jsou urychlovače. Ty nám mohou posloužit jako intenzivní zdroje směrovaných elektronových, mionových a tauonových neutrin. A právě třeba přeměnu tauonových neutrin jinak studovat nemůžeme. V současnosti existuje několik urychlovačů, které vytvářejí svazky neutrin a posílají je do vzdálených neutrinových detektorů. V tomto případě se zatím vždy vytváří intenzivní svazek mionových neutrin tak, že se ve srážkách protonů urychlených na rychlosti blízké rychlosti světla s jádry terče produkuje velké množství mezonů. Ty se pomocí magnetického pole namíří správným směrem a za letu dlouhým tunelem se pak rozpadají za vzniku mionu a mionového neutrina. Zbývající nabité mezony a protony se absorbují na konci tunelu a miony pak pohltí vrstva země, kterou neutrina bez problému prolétají. Dostaneme tak relativně velmi čistý svazek mionových neutrin.

Nejznámější je urychlovač v japonské laboratoři KEK, který svazek neutrin posílá směrem ke 250 km vzdálenému detektoru Super-Kamiokande. Tento experiment se označuje jako K2K a během měření se podařilo zachytit 112 mionových neutrin oproti 158, které by měly být detekovány v případě, že nejsou oscilace. Podařilo se určit i energie těchto neutrin. Z úbytku a energetického spektra se stejně jako z atmosférických neutrin podařilo získat informace o rozdílu kvadrátu hmotností druhého a třetího typu neutrin a velikost jejich vzájemného míchání. Výsledky jsou v dobré shodě.

Zvětšit obrázek

Oscilace elektronových antineutrin produkovaných reaktorem a pozorované některým z budoucích velmi přesných experimentů. Oscilace odpovídají energii neutrin 4 MeV. Hluboké oscilace na vzdálenostech desítek až stovek km jsou způsobeny mícháním prvního a druhého typu neutrin. Plytké, rychlé oscilace, které se na ně nakládají, jsou způsobeny mícháním prvního a třetího typu neutrin (předpokládá se hodnota úhlu ϴ13 okolo 8 stupňů).

Na úspěchy experimentu K2K navázal projekt T2K (Tokai-to-Kamioka), který využívá k vytváření svazku mionových neutrin protonový urychlovač laboratoře J-PARC (Japan Proton Accelerator Research Complex) umístěný v městě Tokai. Neutrina ve svazku uletí 295 km, než proletí detektorem Super-Kamiokande. V listopadu 2009 se podařilo zachytit první neutrina detektorem v blízkosti urychlovače, který má testovat kvalitu a parametry neutrinového svazku. A koncem února letošního roku se podařilo zachytit první neutrina detektorem Super-Kamiokande. Nyní se bude pomalu zvyšovat intenzita svazku neutrin a nakonec by měla být stokrát větší než u experimentu K2K. Postupně by se tak mělo začít s intenzivním studiem oscilací.

Experiment s názvem MINOS využívá už zmíněný „železný“ detektor neutrin Soudan 2. Svazek neutrin, který k němu ze vzdálenosti 730 km letí je produkován urychlovačem v americké laboratoři Fermilab, kde je také známý urychlovač Tevatron. Také tento experiment pozoruje pomocí úbytku mionových neutrin projevy jejich oscilací ve shodě s výsledky experimentu K2K.

Zvětšit obrázek

Detektory v blízkosti zdroje neutrin produkovaných urychlovačem J-PARC pro experiment T2K (zdroj T2K).

Dalším podobným typem experimentu je CNGS (CERN to Gran Sasso). V tomto případě urychlovač v laboratoři CERN posílá neutrinový svazek směrem k 750 km vzdálenému detektoru v podzemní laboratoři Gran Sasso v Itálii. Jeho specialitou by měla být detekce tau neutrin, která by díky oscilacím vznikla. Kvůli tomu se staví pro Gran Sasso speciální detektor OPERA, který se skládá střídavě z železných plátů a fotografické emulze. V minulých dvou letech se podařilo rozběhnout a nabrat zkušenosti z produkcí svazku mionových neutrin. Zatím však nebyla intenzita dost veliká, aby mohlo být v Gran Sasso nějaké tauonové neutrino zachyceno. V příštích letech by mělo dojít k takovému pokroku, aby se studium oscilací mionových neutrin pomocí zachycení vzniklých neutrin tauonových mohlo začít.

Mezi budoucí experimentální možnosti se řadí i získání velice čistých svazků elektronových neutrin s přesně danou energií. Tuto možnost by mohly poskytnout urychlovače radioaktivních jader. Tato jádra by se urychlila na rychlosti blízké rychlosti světla. Pak by se vyvedla do shromažďovacího prstence, jenž by obsahoval dlouhý rovný úsek, který by směřoval ke vzdálenému neutrinovému detektoru. Energie rozpadu radioaktivních jader je malá, takže směr pohybu a kinetická energie vzniklého neutrina by byla dána právě pohybem radioaktivního jádra, při jehož rozpadu vzniklo. Dostaneme tak přesně směrovaný svazek elektronových neutrin s přesně danou energií. Tu můžeme měnit pomocí změny kinetické energie, na kterou urychlíme radioaktivní jádro. Podobnou možnost by pro mionová neutrina poskytovaly svazky mezonů pí sekundárně urychlené na přesně danou energii.

Současný stav poznání oscilace neutrin

Zvětšit obrázek

Hierarchie hmotností neutrin není známa (existují dvě možnosti) není známa ani absolutní hodnota těchto hmotností (zdroj: stránky experimentu COBRA)

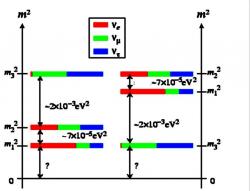
Uveďme si nyní přehledně současný stav výzkumu oscilací neutrin, jak je shrnuje organizace Particle Data Group, která průběžně kompiluje data o vlastnostech elementárních částic. Z měření neutrin ze Slunce a oscilací neutrin z reaktorů se podařilo určit rozdíl kvadrátů hmotnosti druhého a prvního typu neutrin Δm₂₁² = m₂² – m₁² = 0,000079(7) (eV/c²) ² a směšovací úhel jejich míchání sin²ϴ₂₁ = 0,31(5), úhel ϴ₂₁ je tedy zhruba 34^o. Je tedy vidět, že toto míchání je velmi intenzivní. Ze studia oscilací reaktorových neutrin se podařilo zjistit, že míchání mezi prvním a třetím typem neutrin je naopak velmi malé sin²ϴ₃₁ < 0,03, úhel ϴ₃₁ tak je menší než 10^o. Kombinací výsledků detekce atmosférických neutrin a experimentů se svazky mionových neutrin produkovaných pomocí urychlovačů se podařilo určit rozdíl kvadrátů hmotností třetího a druhého typu neutrin Δm₃₂² = m₃² – m₂² = 0,0026(4) (eV/c²) ² a směšovací úhel jejich míchání sin²ϴ₃₂ = 0,45 s přesností zhruba 30 %, úhel ϴ₃₂ je tedy zhruba 42^o.

Jak už bylo zmíněno v úvodu tohoto článku, nelze pomocí oscilací určit hmotnost neutrin. Také nelze určit, které z nich má hmotnost nejnižší. Takže existují různé kombinace pořadí hmotností neutrin, které z měřených rozdílů kvadrátů jejich hmotností můžeme získat. Absolutní hodnoty hmotností a pořadí je třeba zjistit jiným způsobem. Stačí pak určit hmotnost jednoho z nich a z údajů získaných v oscilacích určíme i hmotnosti ostatních. Jedna z cest - studium energie elektronů produkovaných v rozpadu tritia, byla popsána v první části cyklu o neutrinech. Pokud by hmotnosti neutrin řádově odpovídaly rozdílům jejich hmotností, byla by jejich hmotnost velmi malá – pod desetinu eV/c². A jen velmi těžko by se tak dala tímto typem experimentu určit. Pokud by hmotnosti neutrin byly mnohem větší než jsou rozdíly mezi nimi, tak bude mít experiment KATRIN, který využívá právě rozpad tritia, šanci. Další možnosti, která by mohla umožnit zvážit neutrina, se budeme věnovat v následujících odstavcích.

Bezneutrinový dvojitý rozpad beta

Na závěr našeho povídání o neutrinech se tak ještě podívejme na jednu jejich vlastnost, která by mohla mít velice zajímavé důsledky a navíc souvisí s hmotnostmi a oscilacemi neutrin. Pokud by ve skutečnosti byly neutrino a antineutrino jednou částicí, mohlo by docházet k tzv. bezneutrinovému dvojitému rozpadu beta. Takový typ neutrina se označuje jako majoránovské. V případě, že se neutrino a antineutrino liší, hovoříme o diracovském neutrinu. Připomeňme si, že neutrina mohou být majoránovskou částicí jen proto, že mají nulový elektrický náboj a magnetický moment. Ty se totiž u částice a antičástice liší. Pokud bude neutrino majoránovskou částicí, bude se lišit pouze v leptonovém čísle. Pokud se však nemusí leptonové číslo zachovávat, může dojít míchání neutrina a antineutrina a k jejich přeměně, i když s velmi malou pravděpodobností. Ta je dána pravděpodobností narušení zachování leptonového čísla.

Než se dostaneme k bezneutrinovému dvojitému rozpadu beta, vysvětleme si pojem dvojitého rozpadu beta. V cyklech o jaderné energetice a využití jaderné energie jsme si několikrát připomínali, že jednotlivé nukleony stejného typu v jádře mají tendenci se párovat. V případě, že se spárují, bude jejich vazebná energie v jádře vyšší a jádro pak bude daleko stabilnější a bude mít i nižší hmotnost než když by párování nukleonů neexistovalo.

Zvětšit obrázek

Izobary s počtem nukleonů A = 76. Střídání izobarů se všemi spárovanými nukleony a těch s jedním lichým neutronem a jedním protonem způsobuje, že existuje dvojitý beta rozpad 76Ge na 76Se. Červená křivka zobrazuje závislost hmotnosti na protonovém čísle pro izobary s lichým počtem protonů i neutronů. Modrá křivka zobrazuje tutéž křivku pro izobary se sudým počtem protonů i neutronů. Černé body označují hmotnosti reálných jader.

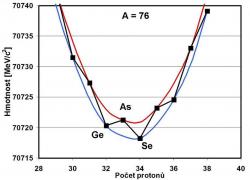
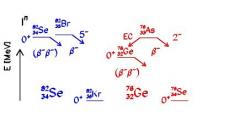
Pro jádra, která mají stejný počet nukleonů a označují se jako izobary, existuje určitý poměr mezi počtem protonů a neutronů, pro které má jádro s takovým počtem nukleonů nejmenší hmotnost a je nejstabilnější z těchto jader. Jádra, která mají oproti němu přebytek neutronů nebo protonů se budou rozpadat rozpadem beta tak, že nakonec skončí u toho nejstabilnějšího izobaru s nejnižší hmotností. Pokud je počet nukleonů ve zkoumaných izobarech lichý, bude vždy jeden nukleon nespárovaný, takže vliv menší vazebné energie spojené s nespárovaným nukleonem bude vždy stejný. Pokud zobrazíme hmotnosti izobarů v závislosti na počtu protonů, tak budou ležet zhruba na parabole a jediné stabilní jádro bude ležet u jejího minima. Pokud však bude celkový počet nukleonů sudý, budou se při beta rozpadu u izobarů střídat jádra, ve kterých jsou všechny nukleony spárované, a jádra, která mají jeden nespárovaný neutron a jeden nespárovaný proton. Budou se tak střídat jádra s vysokým vlivem nespárovaných nukleonů na vazebnou energii a jádra, u nichž žádný nespárovaný nukleon není. Hmotnosti jednotlivých izobarů, zobrazené v závislosti na počtu protonů, tak v tomto případě budou ležet na dvou parabolách a to vždy střídavě. V tomto případě může existovat více stabilních jader. Navíc může dojít k situaci, kdy bude izobar, kterého počet protonů se liší o jeden, mít větší hmotnost a naše jádro se rozpadem beta na něj rozpadat nemůže (naopak toto sousední jádro se bude rozpadat na něj), avšak izobar který se liší v počtu protonů o dvojku, bude mít hmotnost menší. V tomto případě se naše jádro může na něj rozpadat, ale musí vyletět dva elektrony a dvě antineutrina – dochází k dvojitému rozpadu beta. Pravděpodobnost takového procesu je však extrémně malá.

Dvojitý beta rozpad může reálně nastat u více než šedesátí různých jader. Ovšem ve většině případu může zároveň docházet i k jinému typu rozpadů a je extrémně těžké jej pozorovat. Povedlo se to zatím zhruba u deseti nuklidů, každý z nich má dobu života danou tímto rozpadem delší než 10¹⁹ let. V případě dvojitého beta rozpadu odnáší část energie dvojice neutrin a součet energie produkovaných elektronů bude v každém konkrétním rozpadu daného izotopu jiná a menší než je energie v rozpadu uvolněná.

Pokud bude neutrino majoranovské a tedy shodné s antineutrinem, mohlo by při dvojitém beta rozpadu dojít k tomu, že se dvě neutrina (neutrino a antineutrino) vzájemně anihilují. Jinak by se to také dalo interpretovat jako pohlcení neutrina vyzářeného jedním nukleonem jako antičástice druhým. Tato neutrina jsou ve formě virtuálních částic a bezneutrinový dvojitý rozpad beta musí proběhnout přes virtuální mezistav. V konečném důsledku se při bezneutrinovém dvojitém beta rozpadu vyzáří pouze dva elektrony. Ty nesou veškerou energii uvolněnou při rozpadu, což je charakteristika, která by měla pomoci bezneutrinový dvojitý beta rozpad identifikovat na pozadí klasického dvojitého rozpadu beta.

Bezneutrinový dvojitý rozpad beta, jak už bylo zmíněno, narušuje zákon zachování leptonového čísla. Ve Standardním modelu je striktně zakázán a i v obecnějších fyzikálních modelech bude probíhat s ještě daleko menší pravděpodobností než dvojitý rozpad beta. A pochopitelně jen tehdy, pokud bude neutrino majoranovské, bude mít nenulovou klidovou hmotnost a budou splněny další speciální podmínky. Jednou z nich je třeba, že musí být možná změna helicity neutrina. O této vlastnosti, která je spojena s orientací projekce spinu (momentu hybnosti) neutrina vůči jeho směru pohybu, jsme si podrobněji psali v první části cyklu. Helicita určuje, zda je částice pravotočivá či levotočivá. Řekli jsme si, že neutrina jsou pouze levotočivá a antineutrina pouze pravotočivá. Takže, pokud se má jednat o stejnou částici, musí být i zmíněná možnost změny helicity.

Ve všech případech bezneutrinového beta rozpadu bude součet energie produkovaných elektronů stejný a téměř tak velký, jako energie v rozpadu uvolněná. Naopak jen velmi málo případů klasického dvojitého rozpadu beta bude mít tuto energii. Díky tomu máme šanci bezneutrinový dvojitý beta rozpad identifikovat i přes jeho extrémně malou pravděpodobnost. Pokud existuje, pravděpodobnost tohoto rozpadu by velmi silně závisela na hmotnosti elektronového neutrina a byla tak ideálním nástrojem pro její určení.

Zvětšit obrázek

Příklady jader, které se rozpadají dvojitým rozpadem beta.U jader je zobrazen počet nukleonů a počet protonů. Klidová energie jader je dána jejich hmotnostmi. Jen je-li klidová energie rozpadajícího jádra vyšší než klidová energie vzniklých produktů, může k rozpadu dojít. Na obrázku jsou uvedeny ještě spiny jader, které také silně ovlivňují pravděpodobnost rozpadu beta.

Experimenty zkoumající dvojitý beta rozpad

Dvojitý beta rozpad je jev s velmi malou pravděpodobností a jádra, která se tak rozpadají, mají doby života, které patří k těm nejdelším doposud měřeným. Proto je třeba experimentální zařízení, které má tento proces pozorovat, co nejvíce odstínit od okolního radioaktivního záření. Kvůli odstínění od částic kosmického záření se tyto experimenty, stejně jako experimenty s detekcí neutrin, umisťují hluboko pod zem. Zároveň musí být příslušná jeskyně, ve které experiment probíhá, v horninách, které obsahují co nejméně radioaktivních prvků. Co nejméně radioaktivních prvků musí obsahovat i materiály, ze kterých se buduje experimentální zařízení.

Hlavní součástí experimentálního zařízení, které studuje bezneutrinový dvojitý beta rozpad, je detektor elektronů. Ten musí mít co největší účinnost pro jejich zachycování a zároveň musí co nejpřesněji určit jejich energii, aby bylo možné odlišit případy klasického dvojitého rozpadu beta a rozpadu bezneutrinového. Velmi výhodné je, pokud dokáže detekční systém určit i dráhu elektronu. V tom případě lze určit, zda dvojice elektronů přiletěla z jednoho místa v oblasti, kde máme vzorek materiálu, jehož jádra se dvojitým rozpadem beta přeměňují. Zároveň lze tak identifikovat případy, kdy elektrony pocházejí z radioaktivity pozadí. Dost často je zkoumaný materiál zabudován přímo do citlivého objemu detektoru, aby se zajistila co nejvyšší pravděpodobnost zachycení každého případu dvojitého rozpadu beta. Okolo detekčního systému se také jako aktivní stínění od radioaktivního pozadí umisťují detektory, které umožňují identifikovat elektrony přicházející z vnějšku.

V posledních desetiletích byla provedena řada experimentů, která studovala dvojitý rozpad beta a zároveň hledala projevy rozpadu bezneutrinového. Izotopy, které jsou vhodné pro studium bezneutrinového dvojitého rozpadu beta a zároveň už u nich byl pozorován klasický dvojitý beta rozpad jsou ⁴⁸Ca, ⁷⁶Ge, ⁸²Se, ⁹⁶Zr, ¹⁰⁰Mo, ¹¹⁶Cd, ¹²⁸Te, ¹³⁰Te, ¹⁵⁰Nd. Z nich nejkratší poločas rozpadu má ¹⁵⁰Nd a ¹⁰⁰Mo (zhruba 0,7 x 10¹⁹ let) a nejdelší ¹²⁸Te (zhruba 2,5 x 10²⁴ let). Pro představu tak u jednoho kilogramu molybdenu proběhne pouze zhruba 500 tisíc rozpadů za rok.

Velice známé je v této oblasti stále vylepšované zařízení s názvem NEMO, které pracuje v podzemní laboratoři Modane v tunelu Frejus mezi Francií a Itálií. Jednotlivá vylepšení sestavy byla označována posupně čísly až po NEMO-III. Detektor má šest metrů v průměru a jeho výška je čtyři metry. Jako zdroj třeba používal 10 kg zmiňovaného molybdenu, také třeba u selenu je snaha přejít k hmotnostem vzorku větším než desítka kilogramů. Jsou dvě cesty ke zlepšení měření a jeho větší citlivosti. Jedním je zvětšování hmotnosti měřeného vzorku a druhou potlačování radioaktivního pozadí. V současnosti se připravuje návrh vylepšená sestava SuperNEMO, která by obsahovala až stovky kilogramů vzorku. Také další navrhované experimenty by měly obsahovat stovky kilogramů vzorku a velmi efektivně potlačovat nežádoucí pozadí.

V současnosti běžícím experimentům se daří pozorovat klasický dvojitý beta rozpad a zpřesňovat hodnoty dob života jader, která se tímto rozpadem přeměňují. Existence bezneutrinového dvojitého rozpadu beta zatím nebyla spolehlivě potvrzena. Hraniční hodnoty pro poločas rozpadu jsou v tomto případě v řádu až 10²⁵ let. Pokud je neutrino majoranovské, tak nám tato hodnota říká, že hmotnost elektronového neutrina je menší než 0,4 eV. V posledních letech se sice objevilo i vyhlášení pozorování bezneutrinového dvojitého rozpadu, které by znamenalo hmotnost zhruba právě okolo 0,4 eV. Toto vyhlášení je však bráno spíše skepticky a určitě potřebuje spolehlivě potvrdit nebo vyvrátit. Nově budované a navrhované experimenty by to měly dokázat a zároveň by mohly umožnit takovou citlivost, která by odpovídala rozdílu hmotnosti druhého a třetího typu neutrina. Pokud by se ve vzdálenějším horizontu podařilo uskutečnit vize detektorových systémů se stotunovými vzorky materiálů s dvojitým beta rozpadem, dostali bychom se na úroveň měřených dob života vůči bezneutrinovému rozpadu beta odpovídajícím hmotnosti neutrina v řádu rozdílu hmotnosti neutrina prvního a druhého typu. V tomto případě už budeme moci spolehlivě rozhodnout, zda je neutrino majoranovské nebo diracovské. Pokud pak je majoranovské, tak určíme i jeho absolutní hmotnost.

Zvětšit obrázek

Detektorový systém NEMO-3 pro studium klasického i bezneutrinového dvojitého rozpadu beta (PhD práce Shiva Kinga).

 

Závěr

Různé hmotnosti neutrin, jejich oscilace, které vedou k nezachování jednotlivých leptonových čísel, a velké směšovací úhly jsou krokem k fyzice za Standardním modelem. Současný Standardní model pro strukturu hmoty a interakce popisuje velice spolehlivě a přesně téměř všechny procesy v částicovém světě. Je jen velmi málo jevů, které dokážeme pozorovat a zároveň leží za jeho hranicemi. A právě oscilace neutrin takovým jevem jsou.

Pokud by se navíc podařilo pozorovat dvojitý bezneutrinový rozpad beta, bylo by to nejen potvrzení o majoranovské povaze těchto částic, ale i ještě o hodně razantnější vykročení do světa nové fyziky za Standardním modelem. Je vidět, že neutrina a zvláště studium jejich oscilací a hmotností má stále obrovský potenciál pro získání fundamentálních poznatků. Jde také o okno k poznávání rozdílu mezi světem částic a antičástic a studované vlastnosti mohly mít obrovský vliv na ty nejrannější počátky vývoje našeho vesmíru i vznik asymetrie mezi hmotou a antihmotou v něm. Proto je studium neutrin tak vzrušující záležitostí, u které se dá čekat v příštích letech řada zajímavých novinek.