Podstatná zákernosť odstredivej sily je v tom, že ak ju pri riešení nejakého príkladu nesprávne použijeme, získané kvantitatívne výsledky budú aj napriek tomu správne (matematické vzťahy pre veľkosť odstredivej a dostredivej sily sú rovnaké – sú to sily akcie a reakcie). A tak nachádzame fyzikálne nesprávne riešenia príkladov na kruhový pohyb dokonca vo vysokoškolských učebniciach a zbierkach.
Jedným z prominentných vinníkov, zodpovedných za zmätky spojené s odstredivou silou, je aj zakladateľ modernej kozmonautiky Wernher von Braun. Ten v sérii populárnych článkov v 60. rokoch minulého storočia (vychádzali v časopise Popular Science Monthly a neskôr v knihe Space Frontier) vysvetľoval pohyb družíc po kruhových dráhach rovnováhou medzi odstredivou a gravitačnou silou. Nuž, aj géniovia majú slabšie chvíľky.
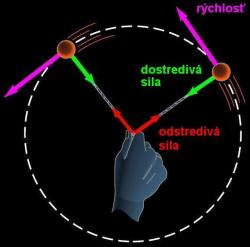
Termín „odstredivá sila“ sa používa na označenie dvoch odlišných druhov síl. Prvý druh odstredivej sily vzniká ako sila reakcie na silu dostredivú. Je to reálna sila – pôvod má vo vzájomnom pôsobení medzi telesami. Má rovnakú veľkosť a opačný smer ako sila dostredivá, no nepôsobí na to isté teleso. Ako príklad uvažujme teleso upevnené na niti (Obr. 1). Niť držíme v ruke a pomocou nej otáčame teleso. Niť prenáša na teleso silu pôsobenia našej ruky. Dostredivá sila je sila, ktorou pôsobí na teleso niť. Odstredivú silu pociťujeme v ruke ako reakciu na silu dostredivú, ktorou pôsobíme na rotujúce teleso. V žiadnom prípade teda nemôžeme povedať, že na rotujúce teleso pôsobí niť a toto pôsobenie vyrovnáva odstredivá sila, vďaka čomu sa teleso pohybuje po kružnici.
Iný typický príklad je pohyb družice okolo Zeme. V tomto prípade je dostredivou silou gravitačná sila, ktorou pôsobí Zem na družicu. Odstredivou silou je gravitačná sila, ktorou pôsobí družica na Zem. Odstredivú silu preto „pociťuje“ naša Zem. S takto definovanou odstredivou silou a jej používaním nie sú spojené problémy.
Nejasnosti a chyby vznikajú pri používaní druhého typu odstredivej sily. Tá je definovaná ako fiktívna alebo kinematická sila, pôsobiaca len v neinerciálnych súradnicových sústavách (SS) – špeciálne v rotujúcich SS. Nie je skutočnou silou v tom zmysle, že nevzniká vzájomným pôsobením medzi telesami, preto sa jej hovorí fiktívna (je to skôr matematický trik). Do kinematickej odstredivej sily prenášame (kinematické) zrýchlenie SS – odtiaľ názov kinematická sila. Aby sme nemuseli neustále počítať so zrýchlením rotujúcej SS, zavedieme odstredivú silu, v ktorej je toto zrýchlenie už započítané. Je to istým spôsobom daň za to, že používame štandardné fyzikálne postupy z inerciálnych SS v neinerciálnych SS.
Teraz sa pozrieme na niekoľko najčastejších chýb spojených s používaním kinematickej odstredivej sily. Začneme od jedného zo základov celej mechaniky – 1. Newtonovho pohybového zákona (ďalšie dva nebudeme až tak potrebovať):
Zákon zotrvačnosti (ZZ) – každé teleso zotrvá v pokoji, alebo v rovnomernom priamočiarom pohybe, kým nie je nútené silovým pôsobením iných telies tento pohybový stav zmeniť.
ZZ hovorí, že najprirodzenejšou vlastnosťou telies je zotrvávať vo svojom pôvodnom pohybovom stave a tým je pokoj, alebo rovnomerný priamočiary pohyb. Jediný spôsob, ako pohybový stav telesa zmeniť (zmeniť smer alebo veľkosť jeho rýchlosti), je pôsobiť naň silou.
Pri mechanickom pohybe dochádza k premiestňovaniu telies. Takýto pohyb je vždy relatívny – určený vzhľadom na vzťažnú SS. Napríklad šofér auta nehybne sedí vzhľadom na sedadlo, ale pohybuje sa vzhľadom na strom pri ceste. Ukazuje sa, že ZZ neplatí vo všetkých SS, ale len v ich špeciálnom type, označenom ako inerciálne SS. V inerciálnej SS sa teleso pohybuje rovnomerne priamočiaro, prípadne zotrváva v pokoji, až kým nebude nútené pôsobením iných telies svoj pohybový stav zmeniť. Pohyb telesa v týchto SS ovplyvňujú len sily, ktorými naň pôsobia iné telesá. S dostatočnou presnosťou sa za inerciálnu SS považuje sústava spojená so stredom Slnka a súradnicovými osami smerujúcimi k vhodným hviezdam. Pri výpočtoch za inerciálnu často považujeme aj SS spojenú s niektorým bodom povrchu Zeme. Ak existuje jediná inerciálna SS, existuje ich nekonečne veľa – každá SS, ktorá vzhľadom k inerciálnej sústave stojí, alebo sa pohybuje rovnomerne priamočiaro, je tiež inerciálna.
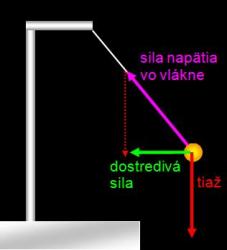
Druhým typom sú neinerciálne SS. V nich môžu telesá meniť svoj pohybový stav, veľkosť, alebo smer rýchlosti aj bez pôsobenia iných telies. Neinerciálne SS sa vzhľadom k inerciálnym pohybujú so zrýchlením. Typickým príkladom sú rôzne rotujúce, či zrýchľujúce SS. V týchto SS neplatí ZZ. Aby sme však mohli používať celú mašinériu, odvodenú pre inerciálne SS, zavedieme fiktívne - kinematické - sily. Je to v skutočnosti len matematický trik. Pri ňom zrýchlenie SS prenesieme z jednej strany pohybovej rovnice na druhú – na stranu síl. Čiže pribudne fiktívna sila, ktorá bude mať opačný smer, než je smer zrýchlenia SS. Uveďme si príklad na objasnenie.
Predstavme si kozmickú loď s vypnutými motormi, dostatočne vzdialenú od planét aj od Slnka. Nepôsobia teda na ňu nijaké sily. V rakete sú dvaja kozmonauti. Jeden sedí v kresle, druhý nehybne visí vo vzduchu. Ak sa raketa vzhľadom k Slnku pohybuje rovnomerne po priamke (alebo sa nepohybuje vôbec), nepôsobí na ňu nijaká vonkajšia sila. SS spojená s takouto raketou bude inerciálna. Ak na kozmonautov v rakete nebudú pôsobiť nijaké sily, budú vzhľadom k rakete v pokoji (nebudú meniť svoj pohybový stav).
V istom okamihu kozmická loď zapne motory a začne sa pohybovať zrýchlene v smere pôvodnej dráhy. Z pohľadu pozorovateľa spojeného so Slnkom sa začne v kresle sediaci kozmonaut pohybovať s rovnakým zrýchlením ako raketa. Musí naň pôsobiť sila a pozorovateľ ju identifikuje ako tlakovú silu, ktorou na kozmonauta tlačí kreslo. Visiaci kozmonaut bude naďalej v pôvodnom pohybovom stave voči Slnku. Steny rakety sa však začnú voči nemu pohybovať. Nakoniec naň narazia, čiže aj jeho rýchlosť voči Slnku sa bude meniť. Kým však sediaci kozmonaut pociťuje neustále tlak kresla, letiaci kozmonaut bude pociťovať silu len počas nárazov na steny rakety. To je pohľad na to, čo sa deje v rakete z hľadiska inerciálnej SS.
Kozmonauti v rakete budú zmenu po zapnutí motorov vnímať inak. Raketa sa začne pohybovať zrýchlene, čiže sa z nej stane neinerciálna SS. Sediaci kozmonaut bude naďalej v pokoji vzhľadom na raketu. Pocíti však, že naň tlačí kreslo, no aj napriek tomu sa nehýbe. Aby kozmonaut vysvetlil svoj pokoj a dosiahol tak formálny súhlas so ZZ, musí zaviesť nový druh sily, ktorá nevzniká pôsobením iných telies, ale vplyvom pohybu SS – kinematickú silu. Tá má rovnakú veľkosť, ale opačný smer ako tlaková sila kresla. Reálne (na svojom tele) ju však necíti. Ešte lepšie to vidieť na druhom kozmonautovi. On zistí, že sa vzhľadom k stenám rakety pohybuje so zrýchlením. Vie, že so zrýchlením je vždy spojené pôsobenie sily. Aby to vysvetlil, zavedie kinematickú silu, hoci on na sebe nijakú silu necíti, ani naň nepôsobí iné teleso. Opäť je to daň za použitie fyzikálnych zákonov „urobených“ pre inerciálne SS v sústave, ktorá nie je inerciálna.
Rovnako je to aj s kinematickým typom odstredivej sily. Nech okolo Zeme rovnomerne po kružnici obieha raketa s kozmonautom. Pozorovateľ v inerciálnej SS vidí, že sa smer rýchlosti rakety neustále mení. Ale podľa ZZ má raketa "snahu" zotrvať v rovnomernom priamočiarom pohybe. Musí preto existovať sila, spôsobujúca zmenu smeru jej rýchlosti. Táto sila musí smerovať do stredu trajektórie (vektor rýchlosti rakety sa tiež stále stáča do stredu) a nazýva sa preto dostredivou. Pre družicu je dostredivou silou gravitácia (rovnaká úvaha bude platiť aj pre kozmonauta). Odstredivou silou bude v tomto prípade gravitačná sila, ktorou pôsobí družica na Zem. Je to sila reakcie na dostredivú silu. Ak by gravitácia prestala na družicu pôsobiť, uletela by rovnomernou rýchlosťou po priamke. Ako keď krútite na niti uviazaným telesom a zrazu niť pustíte. Teleso uletí v smere dotyčnice ku kružnici. V tomto prípade bola dostredivou silou sila vašej ruky.
Ako sa na celú vec pozerá kozmonaut v rakete? Ten vie, že naň pôsobí gravitačná sila, no vzhľadom k rakete je v pokoji. Výsledná sila naň pôsobiaca musí byť nulová a on musí zaviesť kinematickú silu, ktorú nazve odstredivou. Tá má rovnakú veľkosť ako gravitačná sila ale opačný smer. Tu je vidieť dôležitý rozdiel. Z hľadiska inerciálnej SS vysvetľujeme kruhový pohyb kozmonauta a potrebujeme nenulovú výslednú silu – dostredivú. Z hľadiska neinerciálnej SS vysvetľujeme státie kozmonauta a preto výsledná sila, ktorá na neho pôsobí, musí byť nulová. Zavádzame preto fiktívnu, kinematickú, odstredivú silu. Je to len dôsledok toho, že sme v SS spojenej s rotujúcou raketou. Ak majú byť v tejto SS telesá v pokoji, musí na ne pôsobiť okrem dostredivej aj odstredivá sila a musia rotovať rovnakou uhlovou rýchlosťou okolo Zeme ako raketa. Odstredivú sila zavádzame len ako odozvu na rotačný pohyb (nie celkom šťastne) zvolenej SS. Túto odstredivú silu telesá „necítia“ ako skutočné sily, vznikajúce pôsobením iných telies. Ona je potrebná len na to, aby sme rozšírili platnosť ZZ aj na rotujúce SS, ktoré sú neinerciálne.
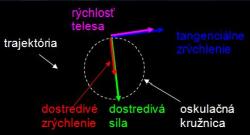
Dá sa úplne všeobecne ukázať, že v inerciálnej SS pri pohybe telesa po ľubovoľnej zakrivenej trajektórii existujú v každom momente pohybu dve zložky zrýchlenia tohoto telesa: dostredivé – smeruje do stredu oskulačnej kružnice, spôsobuje zmenu smeru rýchlosti telesa a tangenciálne (dotyčnicové) – smeruje v smere dotyčnice ku trajektórii, spôsobuje zmenu veľkosti rýchlosti telesa (Obr. 3). V každom momente naň tak pôsobí sila, smerujúca do stredu oskulačnej kružnice – dostredivá sila a sila smerujúca v smere dotyčnice ku trajektórii.
Ak teda na otázku prečo raketa obieha okolo Zeme po kruhovej dráhe odpoviete: „Pri obehu rakety na ňu pôsobia sily – gravitačná príťažlivosť Zeme a odstredivá sila, ktoré sú pri kruhovom pohybe v rovnováhe“, odpovedali ste zle. Ak by na raketu pôsobili dve sily, ktorých účinok sa vykompenzuje, bude sa raketa pohybovať rovnomerne priamočiaro, alebo bude stáť. Podľa zadania totiž sledujeme pohyb družice v inerciálnej SS. V nej vyšetrujeme kruhový pohyb a musíme hľadať dostredivú silu! Aby sme mohli používať kinematickú odstredivú silu, lebo o tú nám ide, museli by sme prejsť do SS rotujúcej spolu s raketou. Raketa by v tejto sústave stála na mieste – výsledná sila, pôsobiaca na ňu, by tak bola nulová.

Vráťme sa k príkladu z úvodu – auto prechádza konštantnou rýchlosťou kruhovú zákrutu. Pri priveľkej rýchlosti takéto auto zo zákruty vyletí. Je to nepríjemná skúsenosť a našťastie ju nezažili všetci. Určite ale každý pocítil, ako je pri prechádzaní zákruty tlačený na dvere auta. Môžeme tieto javy vysvetliť bez odstredivej sily?
Auto má snahu zotrvávať v rovnomernom priamočiarom pohybe. Pri prechádzaní zákruty sa však smer rýchlosti auta mení, takže naň musí pôsobiť dostredivá sila. Dostredivou silou je v tomto prípade trecia sila medzi pneumatikami a asfaltom. Čím je toto trenie väčšie, tým rýchlejšie môžete prechádzať zákrutu, prípadne si môže trúfnuť na zákrutu menšieho polomeru. Preto sú také dôležité dobré pneumatiky a preto musí šofér na mokrej ceste znížiť rýchlosť prechádzania zákrut (trecia sila medzi mokrou cestou a pneumatikou je menšia). Ak ide auto do zákruty príliš rýchlo, veľkosť trecej sily nie je dostatočná na potrebnú zmenu smeru jeho rýchlosti. Pri takejto rýchlosti by trecia sila danej veľkosti stačila na prechod zákruty s väčším polomerom. Čím je totiž polomer zákruty menší, tým väčšia dostredivá sila musí na teleso pôsobiť (viac sa musí meniť smer rýchlosti). Auto preto začne „vynášať“ – sleduje totiž kružnicu s väčším polomerom. Čiže vyletenie auta zo zákruty, nesprávne pripisované odstredivej sile, je v skutočnosti spôsobené nedostatočne veľkou dostredivou silou. A takáto chyba sa vyskytuje veľmi často.

Človek v aute je tiež len teleso. Jeho slobodná vôľa mu umožňuje porušovať morálne zákony ale zákony fyziky porušiť nemôže. Zotrváva preto v priamočiarom rovnomernom pohybe. Aby sa pohyboval v zákrute spolu s autom, musí naň pôsobiť dostredivá sila. V jeho prípade je dostredivou tlaková sila dverí. Netlačí teda do dverí preto, že je vynášaný odstredivou silou, ako si mnohí mysia. Naopak, dvere tlačia na neho a tak ho „dotlačia“ do pohybu po kružnici. Odstredivá sila v tomto prípade pôsobí na dvere automobilu. Je to reakcia na silu, ktorou pôsobia dvere na nás. Táto odstredivá sila je reálna, lebo vzniká vzájomným pôsobením dvoch telies – dverí auta a pasažiera. Extrémnejší príklad na takýto typ pôsobenia je vidieť aj na Obr. 5.
A ešte posledný príklad na auto v zákrute. Predstavte si, že máte na palubnej doske položený mobil. Trenie medzi mobilom a plastom na palubovke je veľmi malé. V zákrute sa teda často stane, že mobil sa pohne a šmýka sa po palubnej doske. Ako to dokážeme vysvetliť z pohľadu inerciálnej SS, čiže bez použitia trecej sily? Mobil mal pred zákrutou svoju rýchlosť. Na zmenu jej smeru je potrebná dostredivá sila. Tou je v tomto prípade trenie medzi palubnou doskou a mobilom. Toto trenie je však malé (preto sa na palubnú dosku pridáva podložka, zvyšujúca trenie, z ktorej sa už mobil neskĺzne). Mobil preto sleduje v podstate svoju pôvodnú rýchlosť, prípadne kružnicu s podstatne väčším polomerom než auto. Zmení sa to, až keď narazí, alebo spadne.
Aby ste sa vyhli rôznym nepresnostiam a omylom je potrebné riešiť príklady na kruhový pohyb z hľadiska inerciálnych SS. V nich nepotrebujete odstredivú silu. A ak by sa Vám aj náhodou zdalo, že odstredivú silu jasne vidíte, respektíve cítite, prejdite do inerciálnej SS, zamyslite sa a zistíte, že všetko je to trochu inak.
Diskuze:



