Podstatná zákernosť odstredivej sily je v tom, že ak ju pri riešení nejakého príkladu nesprávne použijeme, získané kvantitatívne výsledky budú aj napriek tomu správne (matematické vzťahy pre veľkosť odstredivej a dostredivej sily sú rovnaké – sú to sily akcie a reakcie). A tak nachádzame fyzikálne nesprávne riešenia príkladov na kruhový pohyb dokonca vo vysokoškolských učebniciach a zbierkach.
Jedným z prominentných vinníkov, zodpovedných za zmätky spojené s odstredivou silou, je aj zakladateľ modernej kozmonautiky Wernher von Braun. Ten v sérii populárnych článkov v 60. rokoch minulého storočia (vychádzali v časopise Popular Science Monthly a neskôr v knihe Space Frontier) vysvetľoval pohyb družíc po kruhových dráhach rovnováhou medzi odstredivou a gravitačnou silou. Nuž, aj géniovia majú slabšie chvíľky.
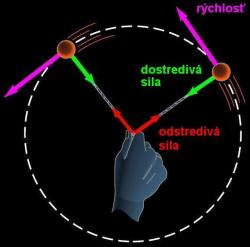
Termín „odstredivá sila“ sa používa na označenie dvoch odlišných druhov síl. Prvý druh odstredivej sily vzniká ako sila reakcie na silu dostredivú. Je to reálna sila – pôvod má vo vzájomnom pôsobení medzi telesami. Má rovnakú veľkosť a opačný smer ako sila dostredivá, no nepôsobí na to isté teleso. Ako príklad uvažujme teleso upevnené na niti (Obr. 1). Niť držíme v ruke a pomocou nej otáčame teleso. Niť prenáša na teleso silu pôsobenia našej ruky. Dostredivá sila je sila, ktorou pôsobí na teleso niť. Odstredivú silu pociťujeme v ruke ako reakciu na silu dostredivú, ktorou pôsobíme na rotujúce teleso. V žiadnom prípade teda nemôžeme povedať, že na rotujúce teleso pôsobí niť a toto pôsobenie vyrovnáva odstredivá sila, vďaka čomu sa teleso pohybuje po kružnici.
Iný typický príklad je pohyb družice okolo Zeme. V tomto prípade je dostredivou silou gravitačná sila, ktorou pôsobí Zem na družicu. Odstredivou silou je gravitačná sila, ktorou pôsobí družica na Zem. Odstredivú silu preto „pociťuje“ naša Zem. S takto definovanou odstredivou silou a jej používaním nie sú spojené problémy.
Nejasnosti a chyby vznikajú pri používaní druhého typu odstredivej sily. Tá je definovaná ako fiktívna alebo kinematická sila, pôsobiaca len v neinerciálnych súradnicových sústavách (SS) – špeciálne v rotujúcich SS. Nie je skutočnou silou v tom zmysle, že nevzniká vzájomným pôsobením medzi telesami, preto sa jej hovorí fiktívna (je to skôr matematický trik). Do kinematickej odstredivej sily prenášame (kinematické) zrýchlenie SS – odtiaľ názov kinematická sila. Aby sme nemuseli neustále počítať so zrýchlením rotujúcej SS, zavedieme odstredivú silu, v ktorej je toto zrýchlenie už započítané. Je to istým spôsobom daň za to, že používame štandardné fyzikálne postupy z inerciálnych SS v neinerciálnych SS.
Teraz sa pozrieme na niekoľko najčastejších chýb spojených s používaním kinematickej odstredivej sily. Začneme od jedného zo základov celej mechaniky – 1. Newtonovho pohybového zákona (ďalšie dva nebudeme až tak potrebovať):
Zákon zotrvačnosti (ZZ) – každé teleso zotrvá v pokoji, alebo v rovnomernom priamočiarom pohybe, kým nie je nútené silovým pôsobením iných telies tento pohybový stav zmeniť.
ZZ hovorí, že najprirodzenejšou vlastnosťou telies je zotrvávať vo svojom pôvodnom pohybovom stave a tým je pokoj, alebo rovnomerný priamočiary pohyb. Jediný spôsob, ako pohybový stav telesa zmeniť (zmeniť smer alebo veľkosť jeho rýchlosti), je pôsobiť naň silou.
Pri mechanickom pohybe dochádza k premiestňovaniu telies. Takýto pohyb je vždy relatívny – určený vzhľadom na vzťažnú SS. Napríklad šofér auta nehybne sedí vzhľadom na sedadlo, ale pohybuje sa vzhľadom na strom pri ceste. Ukazuje sa, že ZZ neplatí vo všetkých SS, ale len v ich špeciálnom type, označenom ako inerciálne SS. V inerciálnej SS sa teleso pohybuje rovnomerne priamočiaro, prípadne zotrváva v pokoji, až kým nebude nútené pôsobením iných telies svoj pohybový stav zmeniť. Pohyb telesa v týchto SS ovplyvňujú len sily, ktorými naň pôsobia iné telesá. S dostatočnou presnosťou sa za inerciálnu SS považuje sústava spojená so stredom Slnka a súradnicovými osami smerujúcimi k vhodným hviezdam. Pri výpočtoch za inerciálnu často považujeme aj SS spojenú s niektorým bodom povrchu Zeme. Ak existuje jediná inerciálna SS, existuje ich nekonečne veľa – každá SS, ktorá vzhľadom k inerciálnej sústave stojí, alebo sa pohybuje rovnomerne priamočiaro, je tiež inerciálna.
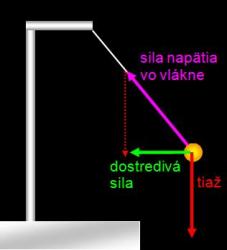
Druhým typom sú neinerciálne SS. V nich môžu telesá meniť svoj pohybový stav, veľkosť, alebo smer rýchlosti aj bez pôsobenia iných telies. Neinerciálne SS sa vzhľadom k inerciálnym pohybujú so zrýchlením. Typickým príkladom sú rôzne rotujúce, či zrýchľujúce SS. V týchto SS neplatí ZZ. Aby sme však mohli používať celú mašinériu, odvodenú pre inerciálne SS, zavedieme fiktívne - kinematické - sily. Je to v skutočnosti len matematický trik. Pri ňom zrýchlenie SS prenesieme z jednej strany pohybovej rovnice na druhú – na stranu síl. Čiže pribudne fiktívna sila, ktorá bude mať opačný smer, než je smer zrýchlenia SS. Uveďme si príklad na objasnenie.
Predstavme si kozmickú loď s vypnutými motormi, dostatočne vzdialenú od planét aj od Slnka. Nepôsobia teda na ňu nijaké sily. V rakete sú dvaja kozmonauti. Jeden sedí v kresle, druhý nehybne visí vo vzduchu. Ak sa raketa vzhľadom k Slnku pohybuje rovnomerne po priamke (alebo sa nepohybuje vôbec), nepôsobí na ňu nijaká vonkajšia sila. SS spojená s takouto raketou bude inerciálna. Ak na kozmonautov v rakete nebudú pôsobiť nijaké sily, budú vzhľadom k rakete v pokoji (nebudú meniť svoj pohybový stav).
V istom okamihu kozmická loď zapne motory a začne sa pohybovať zrýchlene v smere pôvodnej dráhy. Z pohľadu pozorovateľa spojeného so Slnkom sa začne v kresle sediaci kozmonaut pohybovať s rovnakým zrýchlením ako raketa. Musí naň pôsobiť sila a pozorovateľ ju identifikuje ako tlakovú silu, ktorou na kozmonauta tlačí kreslo. Visiaci kozmonaut bude naďalej v pôvodnom pohybovom stave voči Slnku. Steny rakety sa však začnú voči nemu pohybovať. Nakoniec naň narazia, čiže aj jeho rýchlosť voči Slnku sa bude meniť. Kým však sediaci kozmonaut pociťuje neustále tlak kresla, letiaci kozmonaut bude pociťovať silu len počas nárazov na steny rakety. To je pohľad na to, čo sa deje v rakete z hľadiska inerciálnej SS.
Kozmonauti v rakete budú zmenu po zapnutí motorov vnímať inak. Raketa sa začne pohybovať zrýchlene, čiže sa z nej stane neinerciálna SS. Sediaci kozmonaut bude naďalej v pokoji vzhľadom na raketu. Pocíti však, že naň tlačí kreslo, no aj napriek tomu sa nehýbe. Aby kozmonaut vysvetlil svoj pokoj a dosiahol tak formálny súhlas so ZZ, musí zaviesť nový druh sily, ktorá nevzniká pôsobením iných telies, ale vplyvom pohybu SS – kinematickú silu. Tá má rovnakú veľkosť, ale opačný smer ako tlaková sila kresla. Reálne (na svojom tele) ju však necíti. Ešte lepšie to vidieť na druhom kozmonautovi. On zistí, že sa vzhľadom k stenám rakety pohybuje so zrýchlením. Vie, že so zrýchlením je vždy spojené pôsobenie sily. Aby to vysvetlil, zavedie kinematickú silu, hoci on na sebe nijakú silu necíti, ani naň nepôsobí iné teleso. Opäť je to daň za použitie fyzikálnych zákonov „urobených“ pre inerciálne SS v sústave, ktorá nie je inerciálna.
Rovnako je to aj s kinematickým typom odstredivej sily. Nech okolo Zeme rovnomerne po kružnici obieha raketa s kozmonautom. Pozorovateľ v inerciálnej SS vidí, že sa smer rýchlosti rakety neustále mení. Ale podľa ZZ má raketa "snahu" zotrvať v rovnomernom priamočiarom pohybe. Musí preto existovať sila, spôsobujúca zmenu smeru jej rýchlosti. Táto sila musí smerovať do stredu trajektórie (vektor rýchlosti rakety sa tiež stále stáča do stredu) a nazýva sa preto dostredivou. Pre družicu je dostredivou silou gravitácia (rovnaká úvaha bude platiť aj pre kozmonauta). Odstredivou silou bude v tomto prípade gravitačná sila, ktorou pôsobí družica na Zem. Je to sila reakcie na dostredivú silu. Ak by gravitácia prestala na družicu pôsobiť, uletela by rovnomernou rýchlosťou po priamke. Ako keď krútite na niti uviazaným telesom a zrazu niť pustíte. Teleso uletí v smere dotyčnice ku kružnici. V tomto prípade bola dostredivou silou sila vašej ruky.
Ako sa na celú vec pozerá kozmonaut v rakete? Ten vie, že naň pôsobí gravitačná sila, no vzhľadom k rakete je v pokoji. Výsledná sila naň pôsobiaca musí byť nulová a on musí zaviesť kinematickú silu, ktorú nazve odstredivou. Tá má rovnakú veľkosť ako gravitačná sila ale opačný smer. Tu je vidieť dôležitý rozdiel. Z hľadiska inerciálnej SS vysvetľujeme kruhový pohyb kozmonauta a potrebujeme nenulovú výslednú silu – dostredivú. Z hľadiska neinerciálnej SS vysvetľujeme státie kozmonauta a preto výsledná sila, ktorá na neho pôsobí, musí byť nulová. Zavádzame preto fiktívnu, kinematickú, odstredivú silu. Je to len dôsledok toho, že sme v SS spojenej s rotujúcou raketou. Ak majú byť v tejto SS telesá v pokoji, musí na ne pôsobiť okrem dostredivej aj odstredivá sila a musia rotovať rovnakou uhlovou rýchlosťou okolo Zeme ako raketa. Odstredivú sila zavádzame len ako odozvu na rotačný pohyb (nie celkom šťastne) zvolenej SS. Túto odstredivú silu telesá „necítia“ ako skutočné sily, vznikajúce pôsobením iných telies. Ona je potrebná len na to, aby sme rozšírili platnosť ZZ aj na rotujúce SS, ktoré sú neinerciálne.
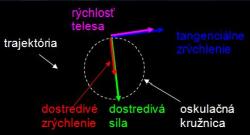
Dá sa úplne všeobecne ukázať, že v inerciálnej SS pri pohybe telesa po ľubovoľnej zakrivenej trajektórii existujú v každom momente pohybu dve zložky zrýchlenia tohoto telesa: dostredivé – smeruje do stredu oskulačnej kružnice, spôsobuje zmenu smeru rýchlosti telesa a tangenciálne (dotyčnicové) – smeruje v smere dotyčnice ku trajektórii, spôsobuje zmenu veľkosti rýchlosti telesa (Obr. 3). V každom momente naň tak pôsobí sila, smerujúca do stredu oskulačnej kružnice – dostredivá sila a sila smerujúca v smere dotyčnice ku trajektórii.
Ak teda na otázku prečo raketa obieha okolo Zeme po kruhovej dráhe odpoviete: „Pri obehu rakety na ňu pôsobia sily – gravitačná príťažlivosť Zeme a odstredivá sila, ktoré sú pri kruhovom pohybe v rovnováhe“, odpovedali ste zle. Ak by na raketu pôsobili dve sily, ktorých účinok sa vykompenzuje, bude sa raketa pohybovať rovnomerne priamočiaro, alebo bude stáť. Podľa zadania totiž sledujeme pohyb družice v inerciálnej SS. V nej vyšetrujeme kruhový pohyb a musíme hľadať dostredivú silu! Aby sme mohli používať kinematickú odstredivú silu, lebo o tú nám ide, museli by sme prejsť do SS rotujúcej spolu s raketou. Raketa by v tejto sústave stála na mieste – výsledná sila, pôsobiaca na ňu, by tak bola nulová.

Vráťme sa k príkladu z úvodu – auto prechádza konštantnou rýchlosťou kruhovú zákrutu. Pri priveľkej rýchlosti takéto auto zo zákruty vyletí. Je to nepríjemná skúsenosť a našťastie ju nezažili všetci. Určite ale každý pocítil, ako je pri prechádzaní zákruty tlačený na dvere auta. Môžeme tieto javy vysvetliť bez odstredivej sily?
Auto má snahu zotrvávať v rovnomernom priamočiarom pohybe. Pri prechádzaní zákruty sa však smer rýchlosti auta mení, takže naň musí pôsobiť dostredivá sila. Dostredivou silou je v tomto prípade trecia sila medzi pneumatikami a asfaltom. Čím je toto trenie väčšie, tým rýchlejšie môžete prechádzať zákrutu, prípadne si môže trúfnuť na zákrutu menšieho polomeru. Preto sú také dôležité dobré pneumatiky a preto musí šofér na mokrej ceste znížiť rýchlosť prechádzania zákrut (trecia sila medzi mokrou cestou a pneumatikou je menšia). Ak ide auto do zákruty príliš rýchlo, veľkosť trecej sily nie je dostatočná na potrebnú zmenu smeru jeho rýchlosti. Pri takejto rýchlosti by trecia sila danej veľkosti stačila na prechod zákruty s väčším polomerom. Čím je totiž polomer zákruty menší, tým väčšia dostredivá sila musí na teleso pôsobiť (viac sa musí meniť smer rýchlosti). Auto preto začne „vynášať“ – sleduje totiž kružnicu s väčším polomerom. Čiže vyletenie auta zo zákruty, nesprávne pripisované odstredivej sile, je v skutočnosti spôsobené nedostatočne veľkou dostredivou silou. A takáto chyba sa vyskytuje veľmi často.

Človek v aute je tiež len teleso. Jeho slobodná vôľa mu umožňuje porušovať morálne zákony ale zákony fyziky porušiť nemôže. Zotrváva preto v priamočiarom rovnomernom pohybe. Aby sa pohyboval v zákrute spolu s autom, musí naň pôsobiť dostredivá sila. V jeho prípade je dostredivou tlaková sila dverí. Netlačí teda do dverí preto, že je vynášaný odstredivou silou, ako si mnohí mysia. Naopak, dvere tlačia na neho a tak ho „dotlačia“ do pohybu po kružnici. Odstredivá sila v tomto prípade pôsobí na dvere automobilu. Je to reakcia na silu, ktorou pôsobia dvere na nás. Táto odstredivá sila je reálna, lebo vzniká vzájomným pôsobením dvoch telies – dverí auta a pasažiera. Extrémnejší príklad na takýto typ pôsobenia je vidieť aj na Obr. 5.
A ešte posledný príklad na auto v zákrute. Predstavte si, že máte na palubnej doske položený mobil. Trenie medzi mobilom a plastom na palubovke je veľmi malé. V zákrute sa teda často stane, že mobil sa pohne a šmýka sa po palubnej doske. Ako to dokážeme vysvetliť z pohľadu inerciálnej SS, čiže bez použitia trecej sily? Mobil mal pred zákrutou svoju rýchlosť. Na zmenu jej smeru je potrebná dostredivá sila. Tou je v tomto prípade trenie medzi palubnou doskou a mobilom. Toto trenie je však malé (preto sa na palubnú dosku pridáva podložka, zvyšujúca trenie, z ktorej sa už mobil neskĺzne). Mobil preto sleduje v podstate svoju pôvodnú rýchlosť, prípadne kružnicu s podstatne väčším polomerom než auto. Zmení sa to, až keď narazí, alebo spadne.
Aby ste sa vyhli rôznym nepresnostiam a omylom je potrebné riešiť príklady na kruhový pohyb z hľadiska inerciálnych SS. V nich nepotrebujete odstredivú silu. A ak by sa Vám aj náhodou zdalo, že odstredivú silu jasne vidíte, respektíve cítite, prejdite do inerciálnej SS, zamyslite sa a zistíte, že všetko je to trochu inak.
Diskuze:
Pohyb družice.
Vladimir Duga,2014-02-15 17:36:19
Ako môže niekto tvrdiť, že družica vplýva na Zem gravitačne, keď nikto ani netuší, ako gravitácia funguje.
Ako môže niekto zamieňať gravitačnú silu za odstredivú? Zo zväčšujúcou sa uhlovou rýchlosťou družice sa zväčšuje aj odstredivá sila. Mám to chápať, že zo zväčšujúcou sa rýchlosťou družice sa zväčšuje aj gravitačná sila družice?
Ak sa prvý Newtonov zákon nedá použiť na pohyb telesa po kružnici, potom je asi nesprávny a treba ho opraviť alebo zrušiť.
...
Stanislav Bandur,2011-09-09 18:58:29
Keby náhodou niekto čítal príspevok do dikusie pridaný skoro dva roku po uverejnení článku, tak ešte pridám:
riešiť pretáčavý či nedotáčavý šmyk na vysvetlenie pre lajkov na niečom tak netriviálnom ako je automobil s nerovnomerným rozložením hmotnosti, kde sily pôsobia mimo ťažiska je fakt úplne od veci.
Veľa plaču pre nič? Alebo ako rodeliť nerozdel...
Stanislav Bandur,2011-09-09 18:48:44
Je síce pekné upresniť si pojmy a povedať si čo na čo pôsobí, ale každá akcia vyvoláva reakciu (a nemám na mysli diskusiu).
Celou diskusiou sa nesie (podľa mňa a aj článok mi dal taký "pocit") že ak niečo, tak potom iné a to je zle, lebo najprv iné a potom niečo. Veď je absolútne jedno či dostredivá alebo odstredivá, veď obe pôsobia súčasne a súčasne aj vznikajú. Ani jeden obrázok totiš nerieši skutočný stav (možno ten s kyvalom, keby sa tam jedna čiara - fialová trošku upravila) Keďže všetky sily pôsobia súčasne, treb uvažovať aj výsledné silové pôsobenie síl (také tie vektory) a z toho by jasne vyplynulo, že auto vyletí zo zákruty preto, že výslednica síl mieri mimo zákrutu. Dostredivou silou nieje tá čo pôsobí medzi pneumatikou a cestou ale výslednica sily ktorá zachováva zotrvačný pohyb telesa a sily ktorá mení smer. A sila meniaca smer je rozložením sily, ktorou sa snaží cesta zastaviť pneumatiku ak dôjde ku kĺzaniu, tak táto sila klesne limitne na nulu a celé je to v háji, lebo rozkladom nuly niči nezískate a vytrvalo sa rútite do jarku v súlade so ZZ.
Ale to by bolo asi na dlhšie a aj s obrázkami, takže nech to je tak či onak je podľa mňa mätúce sily akokoľvek rozdeľovať a určovať, ktorá vyvoláva ktorú.
Děkuji za článek,
Jan Poslušný,2009-12-28 14:36:30
ačkoliv pro mne nepřinesl nic nového. Myslím si však, že čas od času nezaškodí, když si populární vědy chtivá veřejnost přečte něco tak zdánlivě banálního, jako je středoškolský výklad o inerciálních a neinerciálních soustavách - alespoň je to něco, co může bez předchozí průpravy plně pochopit i běžný smrtelník. Tím samozřejmě nechci snižovat ty ostatní články :>)
Čistě z didaktických důvodů bych však nepoužíval příklady, kde gravitace hraje podstatnou roli, alespoň ne v prvním článku. Vagónek pohybující se bez tření po vodorovných kolejích, jednou rovnoměrně přímočaře, podruhé s konstantním vektorem zrychlení, potřetí rovnoměrně po kružnici může osvětlit vše podstatné - na plošině vagónku lze provádět různé experimenty a lze je vykládat z hlediska obou typů vztažných soustav.
Hmmmm....
Petr Balik,2009-12-27 17:13:21
Nejsem fyzik a zrejme proto se dokazu trochu povznest a pochopit proc autor napsal clanek. Nekteri diskutujici se zrejme uz videli coby oponenti habilitacni prace :-)). Muj dik patri autorovi za novy pohled, ktery nam, neodbornikum umoznil. Ale skoro jsem usnul pri cteni tak dlouheho vysvetlovani a nakonec mi pripadlo, ze puvodni jasna myslenka autora se tak nejak v te prehrsli objasnovani skoro vytratila... :-))
Petr Zima,2009-12-28 07:56:49
Je pravda, že tu děláme velblouda z gymnaziální fyziky, ale s tím začal autor :) Ten se také zcela drží tohoto elementárního pohledu, já chtěl ukázat, že to není ten "jediný správný" pohled na věc, jak článek vyznívá, a vhodné užití odstředivé síly má ve fyzice také své místo.
Také nejsem fyzik.
Ota Beran,2009-12-28 09:50:09
Na první pohled, mi článek připadl jako zbytečný. Na druhé přečtení jsem se musel přiklonit k názoru pana Wagnera, že je namísto vysvětlujícího spíše zatemňující. Je mi docela jedno, jestli je česky nebo slovensky, je to jen příliš mnoho zbytečných slov o středoškolské fyzice, generující některé nevhodné příklady v diskusi. Například auto, dostředivá, odstředivá síla a jeho "hodiny" je jako příklad, dáma mi promine, docela hovadina nikoliv oslovina.
Přeji všem čtenářům i autorům Osla příjemný zbytek roku a úspěšné vykročení do toho nového.
pane Berane
Dagmar Gregorova,2009-12-28 16:49:15
Ad: "Například auto, dostředivá, odstředivá síla a jeho "hodiny" je jako příklad, dáma mi promine, docela hovadina nikoliv oslovina."
Pane Beran, dáma nepromine a FAKT se těší na Vaše správné fyzikální vysvětlení (a pojmenování) sil, které působi na auto v zákrutě. I když nejste fyzik, tak víte kde pravda je a co je a co není hovadina.
Pán není fyzik, ale...
Ota Beran,2009-12-28 20:46:02
Už jednou jsem upozornil, že nejsem fyzik, a tak se i přes vaši výzvu necítím být povolán k tomu, abych vám cokoliv v tomto oboru vysvětloval. Měl jsem pocit, že nevhodnost příkladu jste pochopila už z diskusního příspěvku pana Petra Zimy.
Nevhodnost příkladu dle mého názoru spočívá hlavně v tom, že auto jedoucí po silnici zatáčkou (na Slovensku zákrutou) není hmotným bodem pohybujícím se po kružnici. Auto totiž není kulička s očkem, kterou máme uvázanou na provázku a můžeme si s ní točit jak chceme. (i když si to možná některé ženy myslí) Dostředivé síly udržující na silnici auto v zatáčce jsou dány působením tření mezi pneumatikami jeho (v ideálním případě čtyř) kol, které se odvalují po povrchu, jež nemá konstantní kvalitu. Poloha těžiště v jedoucím autě se mění i kola mění svoji polohu, vzhledem k tomuto těžišti. Nic z hlavních faktorů není natolik konstantní, aby automobilové “hodiny” (rotaci auta kolem svislé osy) bylo možno bez uzardění použít jako jednoduchý fyzikální příklad zaviněný převládnutím dostředivé síly na auto.
Nyní se přesuneme od fyziky k automobilové praxi a “teorii hodin”. Podle polohy těžiště v okamžiku, kdy se auto dostává do smyku se auta dělí na přetáčivá a nedotáčivá. Nedotáčivá mají snahu zatáčku opustit po její tečně, zatímco přetáčivá mají tendenci udělat „hodiny“ (otočit se kolem své svislé osy). (samozřejmě na nedotáčivost či přetáčivost má vliv nejen těžiště auta, dané uložením a rozložením jeho nejhmotnějších součástí – motoru a převodovky, dále rozložení cestujících a nákladu, ale i různá kvalita pneumatik, či poháněná náprava…) To, že se auto začne na svých smýkajících se kolech točit kolem své svislé osy, tedy udělá hodiny, souvisí se spoustou dalších vlivů, takže zjednodušení, že převládla dostředivá síla, tak auto dostalo „hodiny“ není dle mého názoru správná a kulhá na všechny končetiny. Nemyslím si jako vy, že auto, které ztratilo adhezi, roztočilo se v „hodinách“ a skončilo vně oblouku zatáčky, bylo přemoženo dostředivou silou. Kdyby tomu tak bylo, tak by dle mého názoru skončilo uvnitř oblouku. Pokud se pletu opravte mne.
Domnívám se, že teď už je čtenářům po mém laickém vysvětlení jasné, proč si myslím, že se nedá rotace auta kolem svislé osy, kterému motoristé říkají „hodiny“ vysvětlit prostým převládnutím dostředivé síly na auto v zatáčce. Možná by čtenáře, stejně jako mne, zajímalo, proč se domníváte, že to možné je a jaké pro to máte vysvětlení.
jak ne-fyzik
Dagmar Gregorova,2009-12-28 22:53:54
nazývá fyzikální sílu, která způsobí, že auto "dostane" takzvané hodiny (čili se dostane do přetáčivého smyku)?
Vím, že existuje i nedotáčivý smyk, ale ten vzniká, když navzdory nadměrné snaze řidiče stočit auto do zatáčky auto z ní vyletí přes vnější okraj. To převládla, jestli se vám to líbí, nebo ne, setrvačná síla nad dostředivou...
Takže když se auto začne přetáčet směrem do zatáčky, jaká fyzikální síla to způsobila? Nerozebírejte počet a rozložení pasažérů, to auto se přetáčí a síla působí ... JAKÁ?
Setrvačná
Jiri Koten,2009-12-29 10:22:09
Nejsem fyzik, ale přetáčivý smyk jsem několikrát dostal a nikdy jsem neskončil uvnitř zatáčky, ale vně. Akorát jsem stál např. proti směru mé jízdy. Zdůvodňuji si to tak, že součástí momentu setrvačnosti je hmotnost a tudíž hmotnější část vozidla "předjede" tu méně hmotnou. Jako celek se ale vozidlo pohybuje pořád po tečně.
no comment
Dagmar Gregorova,2009-12-29 22:03:56
http://www.stockcarscience.com/scienceTopics/scsRacing_CentrifugalForce.php
The forces on a turning car are complex. When you are in a car turning, you feel like you're being pushed toward the outside of the turn. People refer to this as the centrifugal force, a term that is a unfortunate because there isn't any force pushing you outward. Centrifugal force is what physicists call a pseudo or a fictitious force, because it doesn't really exist.
The force that makes a car turn is called the centripetal force. Centripetal literally means "toward the center". Imagine having a tennis ball with a string attached to it.
So is the centrifugal force isn't real, why do you feel like there's something pushing you out the right-side window when you take a turn at high speed? The answers lie in Newton's laws of motion.
A tak...
???
Peter Gina,2010-01-04 09:17:03
Dostredivá sila a odstredivá sila majú takú istú veľkosť a taký istý vzorec, len sú opačne orientované.
Ako by potom bolo možné, aby jedna prevládla a mala zodpovednosť za automobilové hodiny, keď majú zo svojej podstaty rovnakú veľkosť a len opačnú orientáciu.
Děkujeme p. Zimovi za teplá, logická vysvětlení.
Josef Lesov,2009-12-27 09:29:45
"Čiže vyletenie auta zo zákruty, nesprávne pripisované odstredivej sile, je v skutočnosti spôsobené nedostatočne veľkou dostredivou silou."
Dostředivá síla ale nemůže existovat bez té odstředivé, takže...., kterým směrem se bude pohybovat auto, když bude dostředivá síla větší, než dostatečná...? :o)
Je to hodně slovenské a Wernher von Braun by nejspíš sešílel, než by podle tohoto návodu zkonstruoval a vypustil raketu na dráhu volného pádu.
Dagmar Gregorova,2009-12-27 11:47:16
AD:
"...kterým směrem se bude pohybovat auto, když bude dostředivá síla větší, než dostatečná...? :o)"
Dostane takzvane "hodiny"
Tato posladna veta je rovnaka v cestine, ako aj v slovencine... ROVNAKO AKO FYZIKA
"Je to hodně slovenské..."
hmmm... vaše odpověď je hodně česká... a bez diskusehodných argumentů
Tak doufám, že jsem to jenom víc nezamlžil
Petr Zima,2009-12-27 13:56:27
Vaše otázka zní spíše jako vtip, ale stejně mi to nedá a upozorním, že není moc dobře položená, neboť neříkáte k jaké soustavě se vztahujete. Odstředivá síla, totiž díky své "nepravosti" či "fiktivnosti" velmi závisí právě na zvolené soustavě.
1) Pohyb auta vzhledem k soustavě spojené se Zemí:
Tuto soustavu můžeme můžeme v dané situaci považovat za inerciální a vše je tedy přesně tak, jak se píše v článku. Tedy žádná odstředivá síla zde nevystupuje a velikost dostředivé síly určuje poloměr obloku, kterou auto opíše, bez ohledu na skutečný poloměr zatáčky. Otázka tedy nedává smysl.
2) Pohyb auta vzhledem k soustavě spojené s autem:
Vzhledem k této soustavě se auto přirozeně nepohybuje a tedy se zde vždy všechny síly musí vyrušit. Pokud tedy působí pouze dostředivá síla způsobená třením a odtředivá síla způsobená neinerciálností vztažné soustavy, musí být přesně stejné velikosti a vyruší se. Otázka tedy opět nedává smysl.
3) Pohyb auta vzhledem k soustavě spojené s fiktivním autem, které danou rychlostí zatáčku ideálně projede:
Tento pohled se nejspíše blíží intuintivní představě, v jejímž rámci lze Vaši otázku položit. V této soustavě působí ta "správná" odstředivá síla, odpovídající rychlosti a poloměru zatáčky. Pokud zde dostředivá síla způsobená třením pneumatik o silnici převýší sílu odstředivou, čehož lze praticky docílit přílišným stočením volantu, auto prostě zahne zahne více než je třeba a dostane mimo silnici dovnitř zatáčky. Složité, že ano?
Jak vidno pohled v bodu 3) možná nejvíce odpovídá intuitivní představě o odstředivé síle, nicméně v bodu 1) bez odstředivé síly je situace jednodušší a méně náchylná na chybu. Z toho důvodu tento pohled autor doporučuje. Otázka "hodin" navrhovaných paní Gregorovou je složitější a jde nad rámec idealizace auta hmotným bodem. Zde bude hrát rozložení hmotnosti auta a určitě také jaký náhon auto má, jak jistě řidiči potvrdí.
Jinak přeji příjemné a teplé (nebo raději hřejivé:) strávení konce roku a mnoho dalších inspirujících úvah o fyzice, ale raději na místě spolujezdce.
Poslední poznámka
Petr Zima,2009-12-27 14:06:46
Z Vaší otázky je také cítit zmatení, které způsobil autor dvojím zavedením odstředivé síly. Pokud chápeme odtředivou sílu jako reakci na sílu odstředivou, pak skutečně jedna bez druhé nemůře existovat a navíc jsou z definice stejné velikosti. Nicméně tento význam odstředivé síly je dost neobvyklý, jak již upozorňoval pan Wagner níže. Pokud jako obvykle chápeme odstředivou sílu jako sílu setrvačnou, pak je dána pouze vztažnou soustavou a existuje nezávisle na "pravé" síle dostředivé, jak je možno vidět na příkladech výše.
Správná myšlenka, ale ...
Petr Zima,2009-12-26 22:53:41
Je pravda, že odstředivá síla či obecně všechny setrvačné síly mají poněkud zvláštní charakter a při řešení fyzikálních problémů, ve kterých (ne)vystupují, je třeba jisté opatrnosti. Z pohledu inerciální vztažné soustavy skutečně tyto síly neexistují a v pohybových rovnicích se nijak neobjevují. Pokud se tedy snažíme popsat pohyb auta v zatáčce ve vztažné soustavě spojené se Zemí (!), bylo by chybou uvažovat kromě síly třecí, gravitační, síly motoru atd. i "jakousi" odstředivou sílu. Jelikož je obvyklé pro takovouto úlohu vycházet právě ze vztažné soustavy spojené se Zemí, mohl by se laik či začínající student fyziky takové chyby dopustit a autor na toto nebezpečí právem upozorňuje.
Inerciální vztažné soustavy mají své značné výhody mimo jiné právě proto, že všechny síly které v nich působí jsou v jistém smyslu "pravé", mající původ ve vzájemném působení těles. Newtonovská mechanika i speciální teorie relativity z těchto výhod ve velké míře těží a formulují pohybové zákony primárně právě vzhledem k inerciálním vztažným soustavám. To však neznamená, že by uvažování jiných vztažných soustav bylo nekorektní či chybné! Pouze zde přestává platit zákon setrvačnosti a i ostatní fyzikální zákony dostávají složitější tvar. V neinerciálních soustavách tedy musíme uvažovat a počítat trochu jinak a jsou to právě setrvačné síly, jejichž působení lze tento rozdíl přičítat. Takový postup je rovněž konzistentní a vede ke stejným výsledkům jako výpočet výpočet v inerciální vztažné soustavě a není tedy žádný fyzikální důvod ho nějak diskvalifikovat.
...
Petr Zima,2009-12-26 23:37:31
Článek na mě působí velmi dogmaticky svým zápalem, s jakým předkládá inerciální vztažné soustavy téměř jako jediný správný pohled, což je důvod proč reaguji. Vhodná až vychytralá volba vztažné soustavy často umožňuje dramatické zjednodušení problému a bylo by neprozíravé se o některé možnosti a priori ochudit. Autor argumentuje tím, že setrvačné síly, které působí v neinerciálních vztažných soustavách, tělesa "nepociťují" a tyto síly tedy nejsou
skutečné. Na tom jak již jsem uvedl něco je, ale preference jednoho správného přístupu a diskuze o "skutečnosti" sil patří spíše do oblasti filozofie či osobní preference a ne do fyziky.
Autor se ani hlouběji nezamýšlí nad tím, co znamená ono "pociťovat" sílu. Pokusme se tedy analyzovat, jak člověk může vnímat sílu, jež na něj působí. Za prvé můžeme cítit tlak jiného tělesa, které se nás přímo dotýká na povrchu těla; na toto silové působení autor poukazuje a jistě ho lze laicky považovat za "pravou" sílu. Kromě toho jsme ale vybaveni také ústrojím rovnováhy, jehož jedna část v jednoduchosti měří zrychlení našeho těla. Toto zrychlení se (opět zjednodušeně) skládá ze dvou složek a to složky gravitační a složky jež je způsobena nerovnoměrným pohybem našeho těla vůči libovolné inerciální vztažné soustavě. Tato druhá složka tedy přímo odpovídá celkové setrvačné síle a provejuje např. ztrátou rovnováhy nebo lehkou závraťí potom co slezeme z kolotoče. Zde se již tedy dostávám do přímeho rozporu s autorem, neboť naše těla přímo vnímají setrvačné síly, byť v součtu se silami gravitačními.
...
Petr Zima,2009-12-27 00:04:05
Výše uvedená chyba autora se nejvýrazněji projevuje na příkladu kosmonauta v raketě jež se volně, tj. s vypnutými motory, pohybuje na oběžné dráze kolem Země. Tento kosmonaut nejenže vizuálně nepozoruje vlastní zrychlení vzhledem k raketě, dokonce ani jeho ústrojí rovnováhy mu nesignalizuje žádné zrychlení, neboť pohyb jeho i celé rakety je vlastně volný pád. Nejvýstiznějším popisem situace kosmonautova ústrojí rovnováhy je právě tvrzení, proti kterému autor bojuje, totiž že se gravitační síla přesně vykompenzuje se silou setrvačnou. V článku je situace vysvětlena následujícím způsobem:
"... Ten vie, že naň pôsobí gravitačná sila, no vzhľadom k rakete je v pokoji. Výsledná sila naň pôsobiaca musí byť nulová a on musí zaviesť kinematickú silu, ktorú nazve odstredivou. ..."
Jak kosmonaut ví, že na něho působí gravitační síla? Protože vidí planetu Zemi? A jak ví že na něj nepůsobí žádná další gravitační síla? Například se může nalézat v těžišti dvojplanety, kde druhá planeta není vidět (třeba proto, že tím směrem nemá raketa okénko:) V takové situaci by byl kosmonat skutečně v klidu i vzhledem k inerciální vztažné soustavě a místo "nepravé" setrvačné síly by na něj působila "pravá" gravitační síla neviditelné planety. Kosmonaut tuto situaci nemůže odlišit od té původní, kdy obíhá osamocenou planetu a tedy nemůže rozlišovat mezi "pravou" silou gravitační a "nepravou" silou setrvačnou.
...
Petr Zima,2009-12-27 00:28:09
Podobné úvahy jako výše uvedená vedly Einstena k formulaci principu ekvivalence, který je jedním z východisek obecné teorie relativity. Tento princip přímo tvrdí, že setrvačné síly mají stejnou fyzikální podstatu jako síly gravitační a jsou popsány stejnými zákony. Mimoto Einstein dospěl k tomu, že inerciální vztažné soustavy (exaktně) neexistují, neboť gravitaci nelze odstínit. Pokud tedy rozlišování na inerciální a neinerciální vztažné soustavy a rozlišování mezi pravými a nepravými silami má alespoň omezený význam v kontextu Newtonovské mechaniky nebo speciální relativity, v kontextu obecné relativity již nemá význam vůbec žádný. Inerciální vztažné soustavy se zde stávají pouhým idealizovaným matematickým modelem a setrvačné síly naopak integrální součástí reality, přesně opačně než autor předkládá v článku.
Chápu, že odborníkům bude můj ne zcela stručný příspěvek připadat stejně zbytečný jako původní článek, ale koneckonců ten jistě nebyl určen teoretickým fyzikům. Ještě jednou bych rád shrnul, že s myšlenkou článku v zásadě souhlasím, vadí přílišná dogmatičnost a malý nadhled. Varování vyplývající z článku by mělo znít spíše "ujasněte si v jaké vztažné soustavě uvažujete a jaké síly jsou zde na místě" místo "používejte vždy inerciální vztažné soustavy".
Dagmar Gregorova,2009-12-24 10:13:15
Budete si myslieť, keď ako jediná budem článok brániť, že ako Slovenka bránim slovenského autora. Ale od tohoto druhu patriotizmu som ďaleko, pre mňa je vo vede najdôležitejšia pravda... alebo aspoň nezdeformovaná snaha o ňu.
Sama by som bez problémov predtým hovorila o odstredivej sile. Po prečítaní si článku som si ale uvedomila, že ak šofér v aute, ktoré sa rúti do zákruty niečo nepodnikne, teda nepribrzdí a nestočí volant, tak ho to "vynesie" (čo je samozrejmé). A to, čo proti tomuto pôsobeniu zákona zotrvačnosti musí urobiť, je že nejakým činom - stočením volantu (čo má za následok všetky následné fyzikálne súvislosti) vlastne vytvorí protipôsobiacu DOSTREDIVÚ silu. Odstredivá sila teda nie je žiadna "nová", reálne existujúca sila. Aj keď je to banalita, osobne ďakujem autorovi za možnosť sa na túto "zabehanú" situáciu pozrieť z iného fyzikálneho uhla pohľadu. A som presvedčená, že niektorí kritici si tieto súvislosti pred prečítaním článku nikdy neuvedomili. Ako dlho je známe, že Coriolisova sila NESPôSUBUJE stáčanie vodného víru v umývadle... a koľko ľudí si to stále myslí? A tiež len preto, že sa to stále dookola opakuje...
Článek o ničem
Zdeněk Jindra,2009-12-23 20:02:01
Málokdy člověk najde takové zbytečné slovíčkaření. To už by mohl psát o tom, že gravitační zákon je vyřízený, protože neodlišuje setrvačnou a gravitační hmotnost, třeba.
Zdá se mi to poněkud zmatečné
Vladimír Wagner,2009-12-23 11:33:22
Při popisu nejen fyzikálních témat bychom měli používat zavedených definic pojmů (viz například Výkladový slovník fyziky, nebo libovolná učebnice klasické mechaniky). Setrvačné síly (Eulerova, odstředivá, Coriolisova), které se také někdy označují jako kinematické, jsou pojmy spojené s popisem neinerciální vztažné soustavy a významně pomáhají při popisu takového systému a řešení úloh, ve kterých se neinerciální vztažná soustava vyskytuje. Autor v článku užívá pojem odstředivá síla v jiném významu a řekl bych, že tím situaci dost zatemňuje. Označovat pojmem odstředivá síla gravitační sílu, kterou působí dané těleso na jiné je podle mého názoru vyloženě nevhodné (nemusí jít o situaci Země a družice, ale třeba dvojhvězda se stejně hmotnými objekty). Zavedení pojmu síly tření při řešení popisovaných úloh je také "účelové" pro řešení popisu ukázaných jevů a nevysvětluje podstatu reálných sil, které tření zbůsobují (za vším v tomto případě stojí elektrické síly). Přesto nezačnu tento užitečný pojem kritizovat a předefinovávat jiným způsobem, než byl ve fyzice zaveden.
A vi pan autor
Tetrachle Sdvdfvsf,2009-12-23 09:20:04
co je to sila, kdyz se tady s ni tak ohani ?
Já bych to nedráždil.
Pan Neznámý,2009-12-23 11:09:10
Článek považuju za hodně velký omyl (slušně řečeno) a nerad bych se dožil toho, abychom kvůli politické korektnosti zaváděli Lagrangián do populárních článků. Podtrženo a sečteno: ta družice se nějak pohybuje a my předpokládáme kruhovou dráhu. Pak nutně řešíme úlohu s vazbou, kde vystupují EFEKTIVNÍ síly, a tudíž rovnováha sil JE na místě. A kdo nepochopí ani tohle, měl by s fyzikou seknout, protože není schopen ani elementární míry abstrakce a není schopen efektivně řešit úlohy.
Pozornější čtení občas nezaškodí,
Jan Valos,2009-12-24 01:43:56
alespoň v případě že chci článek kritizovat. Protože v článku je výslovně uveden že u příkladu s družicí je pojmenování odstředivá síla v pořádku. Podle mne nelze nesouhlasit s tvrzením že v případě "výletu" auta ze zatáčky není síla která auto dostala mimo vozovku síla odstředivá. Mimo vozovku ho totiž poslala (kromě chyby řidiče, tu samozřejmě neuvažujeme) - setrvačnost. Vozidlo prostě jen mělo snahu SETRVAT v přímočarém pohybu, a že mrcha zatáčka potřebuje k průjezdu něco jiného na tom nic nemění. Jinak je pravda že článek je zbytečně dlouhý a podrobný, tohle se dá sepsat v jednom odstavci.
jan valos:
Palo Priezvisko,2010-01-06 09:51:42
samozrejme ze zotrvacna, ale jedna zlozka posobiacich sil na teleso ktoru subjektivne vnimame najviac smeruje od stredu smerom von a preto sa ludovo nazyva odstrediva(najviac reflektuje ludsku skusenost nieco ako ludsky pocit ze milion korun je uz hodne penazi. pre bezny zivot je to najpresnejsi popis, pretoze odraza ocakavane spravanie a da sa podla neho riadit)
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce



