(Nasledujúci text nepribližuje nové výsledky výskumu, ale vznikol na základe diskusie, ktorá sa rozvinula pod článkom Dešifrovali sme posolstvo supernovy z raného vesmíru. Snaží sa o čo najjednoduchšie vysvetlenie rozdielov ako vzniká červený posun v spektre elektromagnetického žiarenia, keď sa vzhľadom na pozorovateľa pohybuje zdroj, alebo sa rozpína celý vesmírny priestor.)
Keď kmitá elektricky nabitá častica
Predstavme si fyzikálne nerealistický obraz: elektrický náboj, napríklad elektrón, len tak nehybne vegetujúci v časopriestore. Siločiary elektrického poľa sa z neho priamočiaro rozbiehajú do všetkých smerov, magnetické pole by sme v jeho okolí nenamerali.
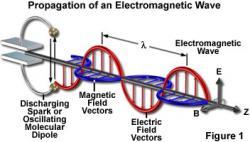
Tento elektrón začne oscilovať, čo už je situácia v reálnom svete bežná. Jeho kmitanie rozvlní predtým „rovné“ siločiary a ak sa to deje vo vákuu, vzruch sa bude priestorom šíriť rýchlosťou svetla, teda takmer 300 tisíc kilometrov za sekundu. Vzniká elektromagnetické vlnenie, ktoré môžeme chápať aj ako prúd fotónov, elementárnych častíc, ktoré predstavujú len kvantá energie a nemajú žiadnu takzvanú pokojovú hmotnosť. Nikdy sa však v pokoji nenachádzajú, sú vlastne len "balíčkami" energie. Sprostredkúvajú elektromagnetickú interakciu, jednu zo štyroch známych fyzikálnych "síl". Zvyšnú trojicu tvorí gravitačná, silná jadrová a slabá jadrová interakcia.
Rýchlosť fotónov vo vákuu predstavuje pre reálny svet absolútny rýchlostný limit, známu hodnotu c = takmer 300 tisíc km/s. Je to práve dôsledok spomínanej vlastnosti - nemajú (pokojovú) hmotnosť, ale sú len energetickými kvantami. Aby hmotná častica dosiahla rýchlosť svetla vo vákuu, musela by byť urýchľovaná nekonečným množstvom energie. A to je nereálne.
Energia, ktorú fotón doslova „stelesňuje“, je priamo úmerná frekvencii žiarenia, teda frekvencii oscilácie zdrojového náboja. Hodnotu tohto fotónového energetického kvanta vypočítame pomerne jednoducho – vynásobením takzvanej Planckovej konštanty (h = 6.62606896×10−34 J.s, alebo 4.13566733×10−15 eV.s) a frekvencie "f" (čiže E = h.f). Čím nižšia je frekvencia kmitania, tým väčšia je vlnová dĺžka vznikajúceho vlnenia a tým je energia fotónu menšia. Výška vlny, čiže amplitúda vlnenia je spätá s intenzitou žiarenia, no v tomto prípade je výpočet o niečo zložitejší. Zjednodušene môžeme intenzitu žiarenia vnímať ako hustotu fotónov s konkrétnou energiou.
Názornú simuláciu ponúka napríklad táto stránka, ktorá sa otvorí aj kliknutím na nasledujúci obrázok:
Na originálnej stránke je animácia vlnenia len pre spektrálnu oblasť viditeľného svetla, ale platí to (až na „farbu“) pre celú škálu elektromagnetického žiarenia. Posuvnými regulátormi pod obrázkom sa dá nastaviť frekvencia, čím sa začne nepriamo úmerne meniť vlnová dĺžka a zároveň priamo úmerne energia. Alebo je možné meniť amplitúdu. Táto zmena sa na predchádzajúcich parametroch neodrazí, prejaví sa v intenzite farby, ktorá znázorňuje intenzitu žiarenia.
Keď sa zdroj žiarenia pohybuje
Predstavme si teraz, že by sme boli schopní zachytávať aj na veľkú vzdialenosť elektromagnetické žiarenie vysielané jediným konkrétnym kmitajúcim nábojom, napríklad spomínaným elektrónom. Pre zjednodušenie predstavy, nech nepôsobia žiadne iné vplyvy, ako napríklad rozpínanie priestoru, či gravitácia. Ak sa od nás elektrón nevzďaľuje, ani sa k nám nepribližuje, čiže naša vzájomná vzdialenosť je stále rovnaká, elektromagnetická vlna, ktorá sa od neho šíri sa taktiež nemení. Blízko elektrónu by sme namerali jej rovnaké parametre, aké nameriame, keď doletí k Zemi. A to bez ohľadu na vzdialenosť. Keby však tento elektrón letel smerom od nás veľkou, ale stálou rýchlosťou, hoci by sa frekvencia jeho oscilácií nezmenila, vlnová dĺžka žiarenia emitovaného smerom k nám by sa zväčšila len vďaka jeho pohybu.
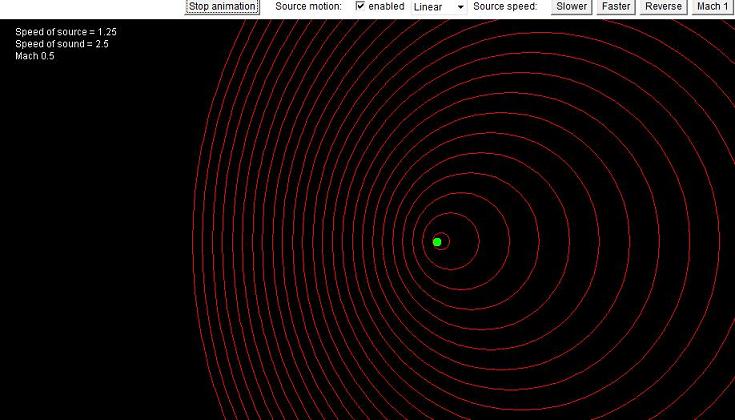
Pre názornú predstavu označme vrcholy vznikajúcej elektromagnetickej vlny farebnou bodkou (viď. obrázok). Od nás sa vzďaľujúci elektrón vysiela tieto značky s menšou frekvenciou (teda za jednotku času ich vyšle menej) v porovnaní so situáciou, keď sa naša vzájomná vzdialenosť nemení. Každá nasledujúca značka je totiž vyslaná z nepatrne väčšej diaľky. Rozdiel predstavuje dráha, ktorú za okamih od vyslania predchádzajúcej značky elektrón prekonal. Práve o tento nepredstaviteľne malý rozdiel vlnová dĺžka narastie. Ak by elektrón letel smerom k nám, situácia by bola opačná, každý vrchol vlny by sa tvoril o nepredstaviteľne malú vzdialenosť bližšie, než jeho predchodca. Tak by približujúci sa elektrón vlnovú dĺžku vlastného žiarenia skrátil (alebo skracoval, ak by išlo o zrýchlený pohyb). Je to vlastne známy Dopplerov efekt, ktorý poznáme z akustiky. Jeho názorné priblíženie ponúka animácia na stránke (otvorí sa aj kliknutím na nasledujúci obrázok),
kde je treba odkliknúť okienko „Source motion enabled“, zvoliť spôsob pohybu „linear“, alebo „circular“ a zvoliť si rýchlosť. Rýchlosť zdroja môže prekročiť rýchlosť, ktorou sa šíri vlna, ako je to v akustike bežné u nadzvukových stíhačiek. Pre elektromagnetické vlnenie šíriace sa vákuom (kde sa zasa zvuk nešíri vôbec) je simulácia platná len, kde sa zdroj pohybuje oveľa pomalšie než sa v ňom šíria vlny.
Keď sa vesmírny priestor rozpína
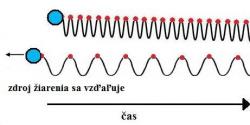
Vráťme sa ale k nášmu kmitajúcemu elektrónu, ktorý k nám vysiela elektromagnetické žiarenie. Umiestnime ho veľmi ďaleko od Zeme, napríklad do vzdialenosti jednej miliardy svetelných rokov, pretože teraz čas bude dôležitý. Fotóny, ktoré oscilujúci vzdialený elektrón vyžiari, by sme v reálnej situácii na takú diaľku nemohli zachytiť, ale myšlienkové experimenty nám takúto predstavu umožňujú. Zrušme aj iné rušivé svetelné a gravitačné zdroje a nechajme vesmír sa rozpínať, čo zodpovedá pozorovanej realite. Priestor, ktorý sa neustále zväčšuje, unáša elektrón preč od každého pozorovateľa, bez ohľadu kde v expandujúcom vesmíre je. Čiže aj vzhľadom na nás sa opäť vzďaľuje. A čím je ďalej, tým jeho únik rýchlejší (Hubblov zákon). Preto ako pozorovatelia nameriame nárast vlnovej dĺžky rovnaký, ako keby sa elektrón vzďaľoval vlastným pohybom stále rýchlejšie. Čo sa však v tejto situácii stane s elektromagnetickou vlnou šíriacou sa priestorom? Opäť si predstavme farebné značky na vrcholoch sínusoidy a uvedomme si, že priestor sa rozpína pomaly, ale vytrvalo – aj ten medzi značkami. Ako povrch nafukovaného detského balóniku.
Urobme typicky „einsteinovský“ myšlienkový experiment (podobné myšlienkové experimenty robil Einstein a vďaka nim dokázal prekročiť hranicu reality na ktorú sme zvyknutí a vykročiť smerom k nepredstaviteľne rozľahlým priestorom a vysokým rýchlostiam, pri ktorých sa nielen zastavuje ľudská predstavivosť, ale aj čas. Vytvoril tak úžasnú teóriu, ktorú dlho po jej publikovaní nemal kto a ako overiť a doposiaľ ju fyzici s nadšením opakovane testujú). Predstavme si, že letíme rýchlosťou svetla povedľa elektromagnetickej vlny emitovanej našim elektrónom a dokážeme ju vidieť ako sínusoidu. Spočiatku by sme si nič nevšimli. Už to je výrazný rozdiel so situáciou, keď sa pohybuje samotný zdroj a vlnenie je pozmenené hneď pri vyžiarení a pokiaľ na neho nepôsobia iné vplyvy sa cestou ďalej nezmení, a to ani po dlhej dobe. Ak však dochádza k expanzii priestoru, potom by sme až po rokoch presným meraním zaznamenali, že vzdialenosť medzi značkami na vrcholoch vlny (vedľa ktorých stále ako pozorovatelia letíme) postupne nepatrne, ale vytrvalo narastá.
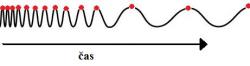
Čiže ak elektromagnetické vlnenie prechádza zväčšujúcim sa priestorom, aj tá malá vzdialenosť medzi značkami sa nepredstaviteľne pomaly stále rozpína a naťahuje vlnovú dĺžku, čim klesá energia žiarenia. V prípade, že sa vesmír zmenšuje, vzdialenosť medzi značkami sa pomaličky postupne skracuje a energia narastá. Na elektromagnetických vlnách sa tak podpisuje nielen rýchlosť, akou sa rozpína, či scvrkáva priestor, ktorým sa šíria, ale aj čas, teda ako dlho sa ním šíria. Preto expandujúci vesmír dokáže za dostatočne dlhú dobu pozmeniť elektromagnetické žiarenie oveľa viac, ako by to dokázal len vlastný pohyb zdroja. Vlnová dĺžka najstaršieho kozmického žiarenia, ktoré dnes vnímame ako mikrovlnné pozadie sa počas asi 13,32 miliardy rokov jeho existencie predĺžila viac ako tisíc násobne.
Svetlo sa posúva do modra a do červena

Mieru skrátenia vlnovej dĺžky stanovujeme pomocou takzvaného modrého posunu (blueschift) a mieru predĺženia pomocou červeného posunu (redshift). Názvy vznikli v dobách, keď sa vesmír pozoroval len v úzkej spektrálnej oblasti viditeľného svetla, v ktorom má červená farba najdlhšiu a modrá najkratšiu vlnovú dĺžku. V súčasnosti sa však tieto pojmy používajú pre skrátenie, či nárast vlnovej dĺžky celého spektra elektromagnetických vĺn, aj keď mimo viditeľnej oblasti to už nemusí zodpovedať realite. Ak sa napríklad infračervenému (tepelnému) žiareniu predĺži vlnová dĺžka, posunie sa v spektrálnej škále smerom k mikrovlnám a od červeného viditeľného svetla sa vzdiali. Napriek tomu opäť pôjde o červený posun (zachováva sa smer posunu). To, čo ale platí bez výnimky pre všetky elektromagnetické vlny je, že ak sa u nich prejaví modrý posun, čiže sa zvýši ich frekvencia a zníži vlnová dĺžka, energia narastie. A naopak – červený posun znižuje energiu žiarenia (E = Planckova konštanta x frekvencia).
Práve energia je to, čo odlišuje nebezpečné ionizujúce žiarenie (od vysokofrekvenčného UV, cez röntgenové lúče po gama žiarenie) od neionizujúceho (viditeľné svetlo, mikrovlny a rádiové vlny). Fotóny ionizujúceho žiarenia majú dostatok energie na to, aby z atómov, do ktorých sa strafia, vyrazili valenčný elektrón, čiže z nich „vyrobili“ ión. V bunkách živých organizmov tak môže dochádzať napríklad k poškodeniu DNA, čo výrazne zvyšuje vznik nádorových ochorení.
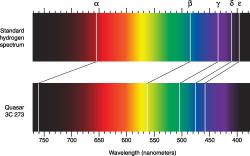
Ale späť do vesmíru. Na elektromagnetickom žiarení ktoré zaznamenáme teleskopmi nie je napísané kedy, z akého zdroja a s akou energiou bolo emitované, ako a kam sa vzhľadom na nás ich zdroj pohyboval, či ako dlho a akým priestorom prechádzalo. Je to len výsledkom našich dlhodobých pozorovaní, poznatkov a teórií, že vieme, ako žiaria hviezdy v rôznych štádiách svojho vývoja, ako kvazary, pulzary, a iné exotické objekty. Určité informácie však svetlo so sebou prináša. Okrem jeho frekvencie a intenzity vieme z neho „prečítať“ hodnotu červeného /modrého/ posunu, ak v jeho spektre odhalíme napríklad absorpčné čiary vodíku. Keď žiarenie preniká oblakmi plynu, ktorého podstatnú zložku vo vesmíre tvorí vodík, jeho atómy absorbujú vlny s frekvenciami odpovedajúcimi jeho ionizačným energiám. Tieto vlnové dĺžky potom v prichádzajúcom spektre chýbajú. Vieme, kde tieto medzery sú v spektre ničím neovplyvneného žiarenia. Ich posun v spektrálnej škále zachyteného svetla odhaľuje, ako sa jeho vlnová dĺžka zmenila.
Nech akokoľvek dlho sa ľubovoľná elektromagnetická vlna šíri priestorom, nech akokoľvek tento priestor naťahuje, či skracuje jej vlnovú dĺžku, alebo nech akokoľvek sa jej zdroj sám pohybuje, jedna vlastnosť jej ostáva nezmenená – vo vákuu sa šíri len známou rýchlosťou c = 299 792 458 metrov za sekundu. Aj vesmírna realita je zložitejšia, než zjednodušené myšlienkové experimenty. Na vlnových dĺžkach žiarenia, ktoré zachytíme v prístrojoch sa podpisujú oba opísané mechanizmy - vlastný pohyb zdroja vzhľadom na Zem i rozpínanie vesmírneho priestoru. Vo všeobecnosti platí, že u astronomicky blízkych vyžarujúcich objektoch prevládajú následky vlastného pohybu, u veľmi vzdialených zas vplyv expandujúceho priestoru.
Video znázorňujúce zmenu emitujúceho žiarenia, ktorú spôsobuje samotný pohyb zdroja voči pozorovateľovi:
Diskuze:
nadsvetelná rýchlosť fotónu
Vlado Gonda,2018-07-06 09:04:35
Mne z toho vyplýva, že každý pozorovateľný červený posuv je dôkaz zdanlivo nadsvetelnej rýchlosti svetla. Prečo ?
Pretože trajektória fotónu má za sebou priestor, ktorým reálne nepreletela. Ako to myslím, vysvetlím na príklade:
Majme dve galaxie G1,G2 priemeru 100000 LY, ktoré sa voči sebe aktívne nepohybujú, ale vzďaľujú sa len vplyvom rozpínania vesmíru. Nech sú v čase t1 ich stredy vzdialené 1 mil.LY. Majme pozorovateľa blízko stredu galaxie G2. V nejakom čase t2 nech sú galaxie vzdialené 2 mil.LY. Pozorovateľ v G2 v čase t2 zachytí svetlo z galaxie G1, ktoré letelo posledných 50000 LY vo vnútri G2, ktorá sa nerozpína. Ale počas tejto doby sa priestor rozopol medzi G1,G2, ktorým zaručene ten fotón nepreletel, lebo v tom čase tam jednoducho nebol. Expandujúci priestor tam "vznikol" za chrbtom letiaceho fotónu. Keďže dráha fotónu, ktorú má za sebou je väčšia, ako tá, ktorým reálne preletel, jeho rýchlosť je zdanlivo nadsvetelná.
laický pohled
Jan Kment,2010-01-11 15:01:15
Předem se omlouvám že otravuju vědecké prostředí naivními otázkami laika. Teprve nedávno jsem se na Oslu dozvěděl, že jsou nejvzdálenější galaxie jaksi "rudě posunutější" než ty bližší, a že se
proto najednou zdá, jakoby se rozpínání vesmíru zrychlovalo, k čemuž je prý zapotřebí jakási temná
energie, neb té "obyčejné" se teoreticky nedostává... Mé opravdu jenom základní znalosti fyziky
(Newton, Kepler) mě učí (aspoň tomu takhle rozumím) že kopne li nehmotný fotbalista do míče ve volném prostoru prostém jakýchkoli dalších vlivů bude se míč od něj pohybovat rovnoměrným přímočarým pohybem (to si po pravdě neumím představit, ale na střední škole se to takhle nějak učí), sotva může silový impulz vyvolat něco nehmotného, ale nechme to tak, další příklad už je lidštější, hmotný fotbalista v témže prostoru kopne do míče a udělí mu setrvačnou rychlost, zároveň ale na něj bude působit svou gravitací a tím ho bude na jeho cestě zpomalovat jako kometu v odsluní a míč se k němu po určité době vrátí, alespoň pokud nebude kop dostatelně silný aby udělil míči únikovou rychlost, pokud však bude kop silnější nad určitou mez (danou pokud vím součinem hmotností) bude se míč vzdalovat (a teď mi prosím vysvětlete v čem se mýlím) - rovnoměrně zrychleným pohybem, protože účinky fotbalistovy přitažlivosti na míč budou slábnout (snad se čtvercem vzdálenosti). Pokud je tahle má konstrukce teoreticky správná (nevím do jaké míry tahle základní fyzika ladí např. s OTR), zdá se mi samozřejmé, že se galaxie vzdálenější od těžiště hmotného vesmíru pohybují rychleji.
Můžete mi prosím odpovědět?
omluva
Jan Kment,2010-01-12 09:59:12
Špatně jsem uvažoval. Míč se nebude zrychlovat, gravitace ho bude stále, jenom čím dál tím méně zpomalovat, čili limitní funkce, restp. 3. kosmická rychlost. Jedině kdyby mu něco stále dodávalo energii, třeba kdyby ve vesmíru stále ještě vznikala hmota. Ale to už jsou jen takové tlachy, takže to můžete celé smazat a děkuju za pochopení!
Kam se ztratí energie fotonu?
František Kříž,2009-11-12 16:34:51
... který se "rozepne" spolu s vesmírem?
... dobrá otázka!
Dagmar Gregorova,2009-11-13 18:09:20
Musím sa priznať, že na túto odpoveď som osobne prikrátka, ale pokúsim sa na to v najbližšom voľnom čase pozrieť. So svojou možnou odpoveďou zatiaľ sama polemizujem, preto dočasne ponúkam odpovede renomovaných fyzikov:
Since energy is conserved, where does the energy of redshifted photons go?
By Peter Newman
The energy of a photon is given by E = hc/lambda, where h is Planck's constant, c is the speed of light, and lambda is its wavelength. The cosmological redshift indicates that the wavelength of a photon
increases as it travels over cosmological distances in the Universe.
Thus, its energy decreases.
One of the basic conservation laws is that energy is conserved. The decrease in the energy of redshifted photons seems to violate that law. However, this argument is flawed. Specifically, there is a flaw
in assuming Newtonian conservation laws in general relativistic situations. To quote Peebles (_Principles of Physical Cosmology_,
1995, p. 139):
Where does the lost energy go? ... The resolution of this apparent paradox is that while energy conservation is a good local concept ... and can be defined more generally in the special case of an isolated system in asymptotically flat space,
there is not a general global energy conservation law in general relativity theory.
In other words, on small scales, say the size of a cluster of galaxies, the notion of energy conservation is a good one. However, on the size scales of the Universe, one can no longer define a quantity E_total, much less a quantity that is conserved.
Alebo obšírnejší článok:
http://arxiv.org/ftp/physics/papers/0511/0511178.pdf
každá vlnová dĺžka narastie ... O ROVNAKÝ NÁSOBOK
Jan Bouzek,2009-11-12 13:39:58
Toto ovšem vede k postupné změně rychlosti světla, pokud ji měříme pevnolátkovou šuplerou (např. iridiovým metrem, což bylo nedávno skutečně pozorováno). Protože pevná hmota je tvořena fotony s krátkou vlnovou délkou, narůstá její velikost při expanzi časoprostoru rychleji, než okolní časoprostor v okolním vakuu.
Dagmar Gregorova,2009-11-12 14:27:10
Prepáčte, asi Vám nerozumiem. Neviem nič o meraní rýchlosti svetla šuplerou, alebo metrom, ale pomocou frekvencie zmien el. a mag. poľa.
Pokiaľ viem, tak elektromagneticky alebo gravitačne "spätá" hmota - nemusí ísť o pevné teleso, ale napríklad o gravitačne viazanú sústavu telies - nepodlieha rozpínaniu priestoru vôbec, pretože tieto fyzikálne interakcie sú nepomerne silnejšie (pôsobivejšie:), než je sila rozpínajúceho sa priestoru. Ak sa rozpínaním priestoru v čase znásobuje vlnová dĺžka, prečo sa Vám zdá, že krátkovlnné žiarenie sa rozpína rýchlejšie... inak som tú záverečnú poznámku nepochopila vôbec...
elektromagneticky "spätá" hmota nepodlie
Jan Bouzek,2009-11-13 09:54:18
To znamená, že pokud při měření rychlosti světla vzdálenost iridiovým metrem a čas pomocí vln světla ve vakuu, rychlost světla se nám bude měnit. Proč tvrdíte, že to nechápete, když jste to právě vysvětlila?
http://www.physorg.com/news64.html
dodatok
Dagmar Gregorova,2009-11-12 11:09:47
V súvislosti s týmto článkom som sa stretla z argumentom: Rozpínanie priestoru je analógiou zrýchleného pohybu. Je?
Predstavme si, že sa v statickom vesmíre vzďaľuje od nás teleso, ktoré vyžaruje na viacerých vlnových dĺžkach elektromagnetického spektra, čo majú vyžarujúce telesá bežne „vo zvyku“. Nech jeho pohyb smerom od nás je rovnomerne zrýchlený. Ako sa s časom mení jeho rýchlosť, predlžuje sa aj vlnová dĺžka každej spektrálnej zložky.
Je to pre pozorovateľa analógia situácie, v ktorej sa jeho vzdialenosť od zdroja mení výlučne rovnomerným rozpínaním priestoru medzi nimi? Odpoveď nie je jednoznačná, ako by Nemci odpovedali : Jein
Pre každú vlnovú dĺžku zvlášť to platí a našli by sme matematicky také zrýchlenie, ktoré by zodpovedalo konkrétnej rýchlosti rozpínania vesmíru. Nie je to však možné pre všetky vlnové dĺžky spolu. V ich červenom posune bude v oboch situáciách rozdiel.
Ak sa zdroj vzďaľuje len priamočiarým rovnomerne zrýcleným pohybom, za nejakú časovú jednotku narastie každá vlnová dĺžka v ktorej vyžaruje O ROVNAKÚ HODNOTU
Ak sa však medzi pozorovateľom a zdrojom v čase rovnomerne rozpína len priestor, každá vlnová dĺžka narastie za časovú jednotku O ROVNAKÝ NÁSOBOK.
Takže po dlhšom čase by sa obe situácie mali na celom spektre žiarenia podpísať rôznym spôsobom. Napokon druhý prípad je dobre zdokumentovaný na poslednom obrázku červeného posunu vzdialeného kvazaru. Každá absorbčná čiara sa posunula o inú hodnotu, ale o rovnaký násobok svojej pôvodnej vlnovej dĺžky. Takže ide o rozpínanie samotného priestoru.
Obrázok predtým (unshifted, redshifted, blueshifted) zasa dokumentuje situáciu, keď sa absorbčné čiary posunuli oproti "neposunutému" žiareniu o rovnakú hodnotu - takže by malo ísť o prejav vlastného pohybu zdroja.
Ak sa mýlim, prosím o opravu. Ďakujem
Ján Padyšák,2009-11-12 14:31:04
Veľmi pekný a názorný článok. Chcel som sa spýtať na červený posun spôsobený dopplerovým javom a rozpínaním vesmíru. Podľa mňa bude pomer posunu čiar u oboch prípadov rovnaký a rozdiel bude iba vo veľkosti posuvu (vo veľkých vzdialenostiach bude pre rozpínanie vesmíru podstatne väčší).
Ako to podľa mňa je:
- na posun spektrálnych čiar má vplyv rýchlosť zdroja v smere od/k pozorovateľovi, nie zrýchlenie (zrýchlenie ale spôsobí, zmeny v rýchlosti a tým aj v posunutí čiar v čase)
- rozpínanie priestoru spôsobuje predĺženie vlnových dĺžok o násobok (zjednodušene si to predstavujem tak, že koľkokrát za zväčší priestor medzi pozorovateľom a zdrojom žiarenia, toľkokrát sa zväčší vlnová dĺžka)
tj
-> lambdaP = lambdaE*konst
- doplerov červený posuv sa podľa anglickej wikipédie počíta prakticky rovnako:
-> z=v/c
-> (lambdaP - lambdaE)/lambdaE = v/c
-> lambdaP = lambdaE*(1+v/c)
keďže lambdaE, v aj c sú konštanty, môžeme napísať:
-> lambdaP = lambdaE*konst
alebo sa v niečom mýlim?
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce