Zvětšit obrázek

Obr. 1 Graf nepárnej funkcie – takáto funkcia je symetrická voči počiatku súradnicovej sústavy.

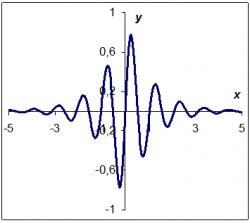
Z matematického hľadiska je so symetriou vždy spojená transformácia, zmena, či už súradníc alebo iných veličín. Takúto transformáciu, symetriu, dokážeme matematicky vyjadriť – napísať ju pomocou vzťahu. Napríklad o funkcii hovoríme, že je nepárna, ak je symetrická voči počiatku súradnicovej sústavy (vyjadruje to transformácia f(x) -> – f(– x), Obr. 1). Hoci nepoznáme explicitný tvar tejto funkcie, vieme hneď niektoré jej vlastnosti (vo fourierovom rozvoji nemá kosínusové členy, integrál z nej v hraniciach symetrických okolo nuly bude nulový,...). Odvetvím matematiky, ktoré sa venuje špeciálne symetriám a ich vlastnostiam je teória grúp. Jej význam vzrástol po tom, čo sa zistilo, že grupy sú veľmi dôležité pre fyziku.
O fyzikálnej teórii hovoríme, že je symetrická (alebo že má symetriu) ak sa rovnice teórie nemenia pri transformáciách spojených s danou symetriou. Špeciálna teória relativity sa napríklad dá odvodiť z požiadavky, aby všetky fyzikálne zákony boli symetrické voči Lorentzovým transformáciám. Ak poznáme symetrie nejakej rovnice, dokážeme oveľa jednoduchšie nájsť jej riešenia, či „uhádnuť“ ich vlastnosti bez toho, že by sme rovnicu riešili, atď. Pravý význam symetrií pre fyziku vedci pochopili až v roku 1917, keď Emma Noetherová zistila, že s každou symetriou je vo fyzike spojený zákon zachovania (Noetherovej teorém). Napríklad zákon zachovania energie je dôsledkom symetrie fyzikálneho systému voči posunom v čase (je jedno, či v teórii počítame dnes alebo pred rokom, rovnice sú rovnaké), zákon zachovania hybnosti je dôsledkom symetrie voči posunutiam v priestore a zákon zachovania momentu hybnosti je dôsledkom symetrie voči rotáciám. Ak sa teda rovnice nejakého fyzikálneho systému nemenia pri zmene (posunutí) v smeroch osí x a z, tak sa bude v tomto systéme zachovávať x-ová a z-ová zložka hybnosti.

Najuznávanejšou teóriou elementárnych častíc (za elementárne považujeme častice, pri ktorých nepozorujeme nijakú vnútornú štruktúru až do úrovne 10^-18 – 10^-19 m) je v súčasnosti Štandardný model (ŠM). Vychádza zo spojenia kvantovej mechaniky a špeciálne teórie relativity. Symetrie sú zabudované v jeho najhlbších základoch. Len pre zaujímavosť uvádzame, že ŠM je postavený na kalibračnej symetrii SU (3) _C x SU(2) _L x U(1) _Y. Pred tým, než sa pustíme do jednotlivých symetrií, spomenieme niekoľko základných faktov o ŠM.

ŠM sa skladá z dvoch základných častí. Do prvej časti patrí 12 fermiónov: 6 kvarkov a 6 leptónov usporiadaných v 3 generáciách (rodinách) s postupne narastajúcou hmotnosťou (Tab. 1). Sú to elementárne častíce, z ktorých je vybudovaná všetka známa hmota. S elektrónmi máme doslova každodennú skúsenosť, hojne sa vyskytujú napríklad vo vodičoch elektrického prúdu. Naopak voľné kvarky sa nikdy nepodarilo pozorovať. Uväznené sú totiž v časticiach: v mezónoch (kvark a antikvark - p mezóny, K mezóny) a v baryónoch (3 kvarky - protóny, neutróny).

Druhou časťou ŠM sú vzájomné interakcie (sily), pôsobiace medzi časticami. Táto časť sa niekedy nazýva aj kalibračný sektor, pretože kalibračné symetrie majú v teóriách interakcií medzi časticami kľúčovú úlohu. Vedcom sa do ŠM podarilo zabudovať 3 interakcie: silnú, elektromagnetickú a slabú. Silná interakcia drží pohromade napr. kvarky v protónoch, či protóny a neutróny v atómových jadrách. Prejavy elektromagnetickej interakcie sú všeobecne známe. Slabá interakcia je zodpovedná napr. za rozpady častíc – rádioaktivitu. Každej interakcii sú priradené aj častice - bozóny, ktoré ju prenášajú (Tab. 2). Poznáme 12 takýchto „prenášačov“ interakcií. Najznámejší je, samozrejme, fotón, sprostredkujúci elektromagnetické interakcie. Silné interakcie prenáša 8 gluónov a W⁺, W^- a Z bozóny sprostredkujú slabé interakcie.

Tab. 1 Základné elementárne častice, vytvárajúce hmotu, podľa ŠM. Pod názvom a značkou častice je jej hmotnosť (pri neutrínach len horný odhad) a elektrický náboj v násobkoch elementárneho náboja. Všetka hmota, s ktorou bežne prichádzame do kontaktu, je vytvorená z častíc 1. generácie.

Tab. 2  Častice sprostredkúvajúce interakcie medzi ostatnými časticami (intermediálne bozóny). Pod názvom častice je jej hmotnosť a elektrický náboj v násobkoch elementárneho náboja. Elektromagnetická a slabá interakcia bola na začiatku 70tych rokov spojená do jedine, elektroslabej interakcie, ale pri bežných energiách sa obe interakcie prejavujú samostatne.

Dosiaľ experimentálne nepotvrdenou zložkou ŠM sú Higgsove bozóny. Tie vysvetľujú pôvod hmotnosti jednotlivých elementárnych častíc. V blízkej budúcnosti sa možno dočkáme objavu týchto častíc na najnovšom urýchľovači LHC v CERNe.

 

 

Obr. 2: Topánka je typická klasická analógia na zmenu parity pri zrkadlení. Ak by sme pravým topánkam pridelili paritu + 1 a ľavým – 1, tak pri zrkadlení by sa hodnota parity menila presne na opačnú, lebo obraz pravej topánky v zrkadle je topánka ľavá a naopak.

Diskrétne symetrie
Prehľad symetrií, používaných v ŠM, začneme diskrétnymi symetriami. Patria medzi ne parita P, nábojová inverzia C, časová inverzia T a ich kombinácie CP a CPT. Parametre týchto symetrií sa menia skokom – diskrétne (napr. smer plynutia času sa zmení na opačný, podobne sa pri týchto symetriách menia smery súradnicových osí či znamienka elektrického náboja častíc). Parita P je len iný názov pre zrkadlenie – otočenie smeru jednej alebo všetkých troch priestorových osí. Ak by ŠM zachovával paritu, deje by prebiehali rovnako v normálnom svete aj v jeho zrkadlovom obraze (inak povedané neexistoval by rozdiel medzi ľavým a pravým, Obr. 2). Nábojová inverzia C je zmena znamienka elektrického náboja. Ak by bol ŠM symetrický voči C symetrii, znamenalo by to, že dej prebehne rovnako, keď všetky častice nahradíme ich príslušnými antičasticami. Časová inverzia T je zmena smeru plynutia času. Rovnice opisujúce správanie sa elementárnych častíc sú voči zmene smeru plynutia času takmer dokonale symetrické. V makrosvete je táto symetria oveľa výraznejšie narušená (entrópia nemôže klesať s rastúcim časom) a doteraz nevieme uspokojivo objasniť, prečo je to tak.  

Zvětšit obrázek

Obr. 3 Schéma Wuovej pokusu. Elektróny vylietavajú pri rozpade jadier Co na jadrá Ni proti smeru spinu jadier. V zrkadle je spin jadier otočený, takže elektróny vylietavajú v smere spinu, presne opačne, než je to v normálnom svete.

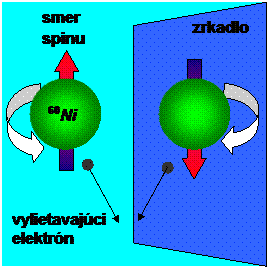
Fyzici si dlho mysleli, že všetky interakcie majú voči symetriám rovnakú „úctu“. V roku 1956 teoretici T. D. Lee a C. N. Yang (Nobelova cena – NC, v roku 1957) navrhli niekoľko experimentálnych testov zachovania parity P v slabých interakciách (zachovanie parity pri elektromagnetických a silných interakciách už bolo vtedy spoľahlivo dokázané). Jeden z návrhov zrealizovala ich kolegyňa C.-S. Wu (Obr. 3) a v roku 1957 dokázala, že parita sa pri slabých interakciách narúša. Wu sledovala b-rozpad jadra kobaltu (je spôsobený slabou interakcou), pri ktorom vzniká jadro niklu, elektrón a elektrónové antineutríno n_e podľa reakcie ⁶⁰Co -> ⁶⁰Ni + e + n_e. Kobaltovú platňu schladenú na teplotu blízku absolútnej nule umiestnila do vonkajšieho magnetického poľa. To spôsobilo orientáciu spinov jadier kobaltu kolmo nad dosku. Takmer všetky elektróny, vznikajúce pri b-rozpade, vylietavali proti smeru spinu jadier kobaltu. Ak by sme sa na tento experiment pozreli v zrkadle (Obr. 3), smery spinov všetkých častíc by sa zmenili na opačné (spin si môžeme predstaviť ako rotáciu častice, a rotácia v smere hodinových ručičiek sa v zrkadle javí presne opačne). Elektróny by aj v zrkadle vylietavali v rovnakom smere, čo by ale bolo v smere spinu jadier kobaltu. To sa však v normálnom svete nepozoruje. Fyzikálne deje, podmienené slabou interakciou, neprebiehajú v zrkadlovom obraze rovnako ako v normálnom svete. Parita sa teda pri slabých interakciách nezachováva. Ukázalo sa, že jej narušenie je dokonca maximálne možné. Zdá sa, že elementárne častice je niekedy vhodnejšie predstavovať si ako topánky než dokonale zrkadlovo symetrické guľôčky. Teoretici tak museli hľadať lepší model slabých interakcií a L. D. Landau predpovedal, že CP bude tá správna symetria, zachovávajúca sa aj pri slabých interakciách.

Pri CP symetrii deje prebehnú rovnako v zrkadlovom svete, ak navyše zameníme častice antičasticami. Aj Wuovej experiment je voči takto definovanej transformácii symetrický. V roku 1964 však J. Cronin a V. Fitch (NC v roku 1980) pozorovali pri rozpade K⁰ mezónov narušenie CP symetrie. Vzhľadom na slabé interakcie tieto častice existujú v dvoch stavoch, typoch. Prvý z nich sa rozpadá na 2 pióny takmer 1000 krát rýchlejšie než sa druhý typ rozpadne na 3 pióny.  Pri oboch rozpadoch sa zachováva CP symetria. Cronin a Fitch pripravili prúd K⁰ mezónov. Prvý typ sa už po prejdení pár cm rozpadol na pióny. Ďalej pokračovali len kaóny druhého typu a po prejdení niekoľkých metrov sa rozpadali na 3 pióny. V 45 prípadoch z 22 700 ale pozorovali rozpad druhého typu kaónov na 2 pióny. To je proces narušujúci CP symetriu. Z počtov jednotlivých prípadov vidieť, že narušenie CP symetrie je veľmi slabé.

V roku 1967 zverejnil A. Sacharov (spolutvorca vodíkovej bomby, NC za mier v 1975) prácu, z ktorej vyplývalo, že narušenie CP symetrie je jednou z troch podmienok, nevyhnutných na vznik miernej asymetrie medzi časticami a antičasticami v počiatočných okamihoch po Veľkom tresku. Vďaka tomu sa nepremenila všetka látka vo vesmíre na žiarenie a mohli vzniknúť hviezdy a nakoniec aj život. Narušenie CP symetrie bolo teda experimentálne dokázané, dokonca sa ukázalo, že mu vďačíme za našu existenciu, ale teoretici nevedeli vytvoriť vhodnú teóriu, opisujúcu tento jav.
Po roku 1971, kedy bola vypracovaná teória zjednotenia elektromagnetických a slabých interakcií, urobili v tomto smere významný krok japonskí fyzici Kobajaši a Maskawa (NC 2008). V tej dobe už vedci vedeli, že K⁰ mezóny sa skladajú z kvarku a antikvarku. Slabé sily vyvolávajú vzájomné premeny medzi kvarkami, oscilácie (na základe analógie s kvarkami bola potom predpovedaná oscilácia neutrín). Japonci modifikovali model opisujúci tieto oscilácie. Na základe matematických argumentov predpovedali, že vtedy známe kvarky na vysvetlenie pozorovaného narušenia CP symetrie pri rozpade K⁰ mezónov nestačia (ich teória so 4 kvarkmi jednoducho nedávala pre istý parameter imaginárnu hodnotu – hodnotu úmernú Ö – 1). Najmenší počet kvarkov, s ktorým vedeli získať dobrý výsledok, bol 6. Predpovedali teda existenciu minimálne jednej novej generácie (rodiny) kvarkov (boli objavené v rokoch 1977 – b kvark a 1994 – t kvark). Ani v súčasnosti však nemožno povedať, že problém narušenia CP symetrie je uspokojivo vyriešený, hoci bol testovaný pri experimentoch ako NA31, NA48 (CERN, Európa), BaBar (SLAC, USA) alebo Belle (KEK, Japonsko).

Po stroskotaní nádejí, vkladaných do CP symetrie, zostáva vedcom už len CPT symetria. Čiže deje v mikrosvete by mali byť úplne symetrické, keď ich sledujete v zrkadle, zameníte častice za antičastice a navyše obrátite chod času (jednoduchšie to možno dosiahnuť zmenou smeru pohybu všetkých častíc na opačný). Ukazuje sa, že nie je možné vytvoriť kvantovú teóriu poľa, v ktorej by bola narušená kombinácia symetrií CPT (automaticky by bola narušená Lorentzova symetria) – ale to môže byť len obmedzenie našej predstavivosti. Keďže je ale narušená CP symetria, hoci jemne, narušená musí byť aj T symetria. Musia teda existovať deje, ktoré neprebiehajú v čase symetricky. Dosiaľ sa nepodarilo nájsť narušenie T symetrie ani CPT symetrie. Ak je ale CPT symetria narušená, mali by sme dokázať napríklad namerať drobné rozdiely v hmotnostiach a dobách života medzi časticami a antičasticami. Takže je to experimentálne testovateľná hypotéza.

 
Spojité symetrie
Pri spojitých symetriách možno spojite meniť parameter symetrie. Sem patria časopriestorové symetrie ako sú rotácie (otočenie súradnicových osí o ľubovoľný uhol) alebo symetrie voči Lorentzovým transformáciám a tiež vnútorné symetrie. Vnútorné symetrie pôsobia na kvantové čísla jednotlivých elementárnych častíc. Častice sú okrem hmotnosti a elektrického náboja charakterizované ešte ďalšími kvantovými číslami ako sú spin, hypernáboj, izospin, farba, ... Čiže tak, ako sa jednotlivé druhy zvierat od seba odlišujú veľkosťou, hmotnosťou, farbou, druhom pokrývky tela a pod., tak sa jednotlivé častice od seba odlišujú svojimi kvantovými číslami. Operácie vnútornej symetrie potom spôsobujú zmeny týchto kvantových čísel, čím vlastne menia jeden typ častíc na iný. Pomocou vnútorných symetrií zostavujeme skupiny príbuzných častíc (môžu sa navzájom medzi sebou meniť) do takzvaných multipletov. Ak by boli vnútorné symetrie dokonalé, častice v multipletoch by mali rovnaké hmotnosti. To sa nepozoruje, lebo niektoré vnútorné symetrie sú narušené. Z veľkosti narušenia potom možno vypočítať rozdiely v hmotnostiach častíc – narušenie týchto symetrií má tak isté výhody.
Opäť si môžeme pomôcť analógiou so systematickou zoológiou. Ak by existovali operácie vnútornej symetrie živočíchov, menili by farbu srsti, počet prstov (kopýt), druh pokrývky tela a podobne. Tieto operácie by dokázali zviera jedného druhu premeniť na zviera iného druhu. V takomto prípade by potom čeľaď reprezentovala multiplet elementárnych častíc – združuje druhy s podobnými vlastnosťami. Využitím vnútorných symetrií v čeľadi mačkovitých šeliem by sme dokázali premeniť mačku divú na leva, leva na geparda, toho na tigra atď. Dala by sa vytvoriť aj matematická štruktúra, opisujúca ako sa druhy menia pri jednotlivých transformáciách. Ak by bola vnútorná symetria dokonalá, mali by všetky zvieratá v čeľadi rovnaké hmotnosti.

Ak sa parametre vnútornej symetrie môžu meniť v závislosti od miesta v priestore, potom takejto symetrii hovoríme kalibračná. Napríklad vlnovú funkciu (úplne charakterizuje stav častice v kvantovej mechanike) môžeme vynásobiť istým číslom (hovoríme mu fáza) bez vplyvu na rovnice teórie alebo na merateľné fyzikálne charakteristiky častice. Ak sa navyše rovnice teórie ani charakteristiky častice nemenia ani vtedy, ak fáza závisí od polohy v priestore (čiže môžeme vlnovú funkciu násobiť dokonca funkciou priestorových súradníc), tak máme teóriu s kalibračnou symetriou U (1). Kalibračné symetrie sú kľúčové k pochopeniu interakcií v ŠM. Spomínaná U (1) kalibračná symetria (presnejšie sa hovorí o grupe) je spojená s elektromagnetickými interakciami a fotónom. Keďže platí Noetherovej teorém, je s kalibračnou symetriou spojený zákon zachovania – konkrétne zákon zachovania elektrického náboja. Iná kalibračná symetria vysvetľuje silné interakcie (a predpovedala 8 častíc prenášajúcich silné interakcie – gluóny). Slabé interakcie možno spojiť s ďalšou kalibračnou symetriou.

Len s využitím kalibračných symetrií pri vysvetľovaní interakcií však fyzici prišli k nepríjemnému výsledku. Ich teória predpovedala, že častice, prenášajúce slabé interakcie – W a Z bozóny, by mali mať nulovú hmotnosť. To ostro protirečilo experimentálnym výsledkom (sú to najťažšie dosiaľ pozorované častice). Našťastie bola pripravená fyzikálna teória, Higgsov mechanizmus, vysvetľujúca, kde sa vzala hmotnosť týchto bozónov. Higgsov mechanizmus by mal objasniť aj pôvod hmotnosti ostatných častíc v ŠM – kvarkov a leptónov. Dôležitou súčasťou tohto mechanizmu je spontánne narušenie symetrie.

 

Obr. 4 Chaotické usporiadanie magnetických domén v NdFeB materiále pred prechodom do feromagnetického stavu.

Spontánne nerušené symetrie
Fyzici elementárnych častíc sa v tomto prípade, nie po prvý krát, inšpirovali fyzikou tuhých látok, kde známy príklad spontánneho narušenia symetrie je feromagnet. Pri dostatočne vysokej teplote je to obyčajný nemagnetický materiál. Mikroskopické magnetické momenty domén, ktoré ho tvoria, sú chaoticky rozmiestnené v priestore, takže feromagnet má rotačnú symetriu a nulovú výslednú magnetizáciu (Obr. 4). Pod istou teplotou (Curieho teplota) dôjde k spontánnemu usporiadaniu jednotlivých magnetických momentov domén a feromagnet, ako celok, získa makroskopickú hodnotu magnetizácie. Tým sa poruší jeho rotačná symetria, pretože jeho vektor magnetizácie určuje v priestore význačnú os. Hoci sú rovnice, opisujúce feromagnet rotačne symetrické, najnižší energetický stav feromagnetu už takým nie je. Feromagnet zostane symetrický už len pri rotáciách okolo osi určenej smerom magnetizácie. S usporiadaním domén sú spojené spinové vlny, ktoré môžeme považovať za častice (odborne kvázičastice) s nulovou hmotnosťou.

Zvětšit obrázek

Obr. 5 Mechanická analógia na Nambuov mechanizmus spontánneho narušenia symetrie. Váza s vydutým dnom je osovo symetrická. Takou zostane aj po vhodení guľôčky presne v smere osi symetrie. Osová symetria sa stratí až v momente, keď sa guľôčka skotúľa do žliabku, do svojho najnižšieho energetického stavu – ten už nie je osovo symetrický.

Ku spontánnemu narušeniu symetrie teda dochádza v prípade, keď rovnice teórie spĺňajú určitú symetriu, no jej najnižší energetický stav, vákuum, ju nezachováva. Ako prví sa spontánnym narušením symetrie zaoberali Nambu (NC v roku 2008) a Goldstone. Dokázali, že každé spontánne narušenie spojitej globálnej symetrie (parameter symetrie je konštantný v celom priestore) vedie ku vzniku nového typu častice - Nambuovho-Goldstoneovho (N-G) bozónu, s nulovou hmotnosťou. 
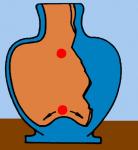
Mechanickou analógiou tohto javu je váza s vydutým dnom (Obr. 5). Váza je symetrická podľa svojej osi. Presne v smere osi symetrie pustíme do vázy guľôčku. Dopadne najprv na vrchol dna. Dostávame opäť osovo symetrický systém, no dlho v tomto stave nevydrží, lebo existuje nižší energetický stav. Po krátkom čase guľôčka skĺzne do žliabku. Vyberie si náhodne jeden konkrétny smer, do ktorého spadne. Dôjde tým k spontánnemu (samovoľnému) narušeniu pôvodnej osovej symetrie systému. Guľôčka sa môže v žliabku pohybovať. Neustále sa tak bude meniť jej stav (poloha v žliabku), hoci jej energia zostáva rovnaká. Na popis zmeny stavu bude postačovať jediný parameter (uhol otočenia okolo pôvodnej osi symetrie) takže energii pohybu guľôčky v žliabku bude zodpovedať jeden typ N-G bozónov. Navyše na zmenu stavu guľôčky v žliabku bude postačovať teoreticky nekonečne malá energia (úplne jemnučké postrčenie), a preto bude mať vzniknutý N-G bozón nulovú energiou a teda nulovú hmotnosť.  

Higgsov mechanizmus je rozšírením teórie spontánneho narušenia na kalibračné symetrie. V tomto prípade nevznikajú nehmotné N-G bozóny, ale častice prenášajúce interakcie získavajú hmotnosť. Nevyhnutnou súčasťou tejto teórie je Higgsovo pole – časticami (kvantami) tohto poľa sú Higgsove bozóny, vypĺňajúce celý priestor. Práve interakciou s nimi získavajú nehmotné častice svoju hmotnosť. V princípe si môžeme priestor vyplnený Higgsovým poľom predstaviť ako nádobu s medom. Keď budeme miešať lyžičkou med, pôjde nám to oveľa ťažšie, ako keď ňou budeme pohybovať v prázdnej nádobe. Je to preto, že spolu s lyžičkou musíme hýbať aj medom. Keby ale o mede v nádobe nevieme, vysvetliť by sme si to mohli aj tak, že lyžička získala v nádobe dodatočnú hmotnosť. Opäť sú takéto prípady známe z tuhých látok. Napríklad s elektrónom v kryštáli môžeme pri výpočtoch narábať ako s voľným, no jeho hmotnosť je iná, ako hmotnosť elektrónu mimo kryštál. Do tejto, tzv. efektívnej, hmotnosti zahŕňame pôsobenie medzi elektrónom a iónmi v mriežke. No a fotón sa v tuhých látkach pohybuje rýchlosťou menšou než vo vákuu, čiže ako častica s nenulovou hmotnosťou, pretože pri svojom pohybe pôsobí aj na okolité častice. W alebo Z bozóny sa teda prejavujú, akoby mali veľkú hmotnosť, pretože na ne pôsobia Higgsove bozóny. Experimentálne ešte neboli tieto častice potvrdené, no CERN a Fermilab intenzívne pracujú na ich objave. Teoretici sú ale pripravení aj na situáciu, že sa Higgs nenájde. Alternatívou k nemu sú teórie ako Technicolor, top kvarkový kondenzát, či model kompozitných W a Z bozónov.

Záver
Predstavili sme si najrôznejšie symetrie fungujúce v svete elementárnych častíc. V rámci stručnosti sme niektoré zaujímavé symetrie radšej ani nespomínali – napríklad supersymetrie (týmto symetriám vďačia superstruny za to, že sú super), ktoré zavádzajú symetriu medzi bozónmi a fermiónmi a predpovedajú celú plejádu nových častíc. Tie dosiaľ nikto nepozoroval a určite by bolo veľmi zaujímavé, keby ich nenájde LHC ani po tom, čo sa mu prestanú zapekať spoje supravodivých magnetov.
Snažili sme sa tiež upozorniť na fakt, že narušenie symetrií nie je pre fyzikov elementárnych častíc nijakou tragédiou. Niektorí idú v tomto smere dokonca tak ďaleko, že uvažujú o narušení Lorentzovej symetrie v extrémne malých (Planckovských) rozmeroch. Učebnice teórie relativity však rozhodne nevyhadzujte. Všetky pozorovania dosiaľ totiž len posúvajú hranice platnosti Lorentzovej symetrie. Efekt jej narušenia, zapracovaný do rôznych rozšírení ŠM, s najväčšou pravdepodobnosťou nebude taký veľký, že by ste s ním pri relativistických výpočtoch bežne museli počítať.

Poznámka redakce: Pro případ, že by některé prohlížeče nezobrazovaly písmena řecké abecedy korektně, je tento článek ke stažení jako dokument ZDE.