Jaká je tedy ta realita? Stručně: Rozloha arktického ledu se blíží normální standardní odchylce. Standardní odchylka je v následujícím grafu označena jako šedý pruh okolo průměrné měsíční hodnoty z let 1979-2007 (černá linka).
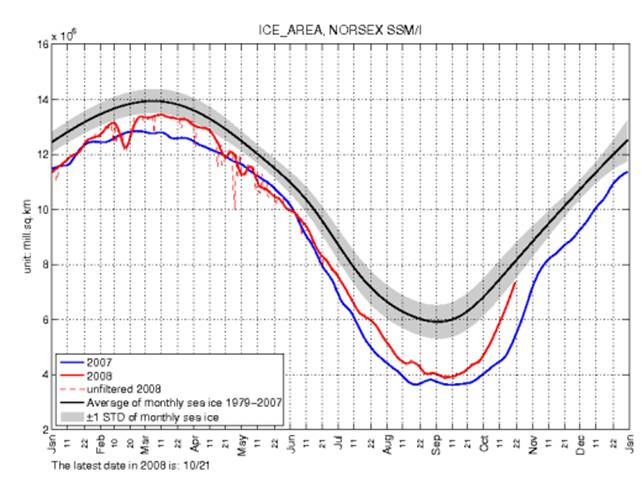
Jak si možná někteří pamatují, kleslo loni zalednění Arktidy na takové minimum, že se mnozí domnívali, že led v Arktidě úplně roztaje. Samozřejmě za mocného působení všech masových medií a internetových bloggerů. Nejen bulvárních novin a plátků, ale také České televize a rozhlasu. Jedni z mála, kdo této hysterii nepodlehli, byli přispěvatelé a čtenáři Osla. Realita je nyní taková, že led v Arktidě neroztál, že se naopak opět rozšiřuje a že zalednění se blíží normálu. I pro mě laika je těžko představitelné, že by 7 metrů silný arktický led roztál během několika sezón.
Pokud někdo neví co je standardní odchylka – což lze u politiků (jsou mezi nimi i právníci a ti statistiku neznají) a novinářů předpokládat – pak vězte: standardní odchylka je vypočítané číslo, které vymezuje hranici normálnosti (vymezuje varianci). Je-li naměřená hodnota menší jak standardní odchylka, pohybuje se naměřená hodnota v rámci normality. Je-li větší, je mimo rámec normálnosti. Standardní odchylka (SO) se vypočítává ze všech získaných hodnot. Hranici „normálnosti“ lze uměle posouvat tak, že se uvažují jak její násobky, tak i záporné hodnoty. Poslední věta je napsána pro naprosté laiky a proto do komentářů prosím nepište, jak to má být správně. Pokud to někoho zajímá, nechť si najde důkladnější vysvětlení na wikipedii nebo v učebnici statistiky. Je-li například nějaká hodnota větší jak tři SO, pak je to velmi ojedinělá hodnota a usuzuje se, že není výsledkem nějaké náhody, ale nějakého „mechanismu“, nebo dokonce i zákona. Hodnoty nad tři SO se totiž stávají v 0,13 procentech případů. Stejně tak u záporných hodnot. Je-li naměřená záporná hodnota větší jak -3 SO, pak se takový jev stává také pouze v 0,13 % případů.
Abychom se ale nevytahovali a nejásali předčasně. Rozloha zalednění ještě není mezi ± 1 SO, tedy mezi 68,26 % případy, ale blíží se k této hodnotě. Na grafu tedy do oblasti šedě namalované. Všimněte si například hodnot z roku 2006. Tehdy zalednění od října do prosince také neproběhlo lineárně. A to znamená, že letošní hodnoty se nemusí vrátit k normálu.
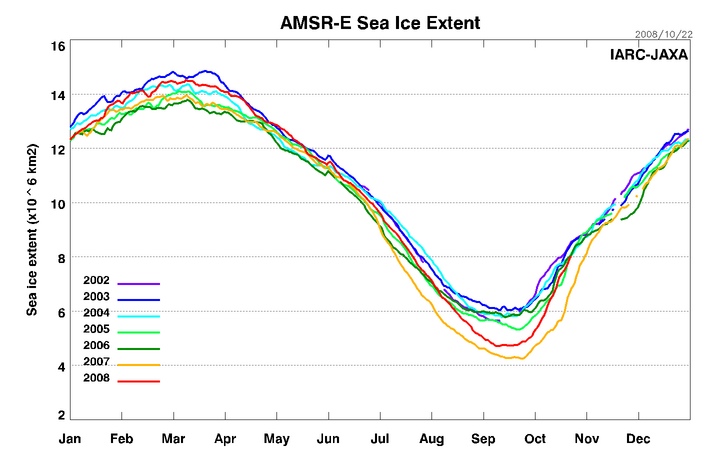
Zdroje:
Nansen Environmental and Remote Sensing Center
IARC-JAXA Information System
Milankovičovy cykly v klimatu na Zemi
Autor: Pavel Kalenda (04.03.2025)
Zalednění Antarktidy přivodil tektonický posun
Autor: Josef Pazdera (26.11.2021)
Zastaví lidstvo nadcházející dobu ledovou?
Autor: Stanislav Mihulka (19.01.2016)
Rozhýbe znečištěný vzduch život v oceánech a ochladí Zemi?
Autor: Josef Pazdera (07.10.2009)
Budú Afričania variť v Kjóto škatuliach?
Autor: Dagmar Gregorová (18.04.2009)
Diskuze:
Re chyba ve skloňování
Jaromir Krepelka,2008-11-13 08:27:46
Pletete si můj genitiv s lokálem, skutečně nemůže být, jak mylně navrhujete, "v letních obdobích posledních dvou rocích".
"dvou roků" versus "dvou rocích&
Igor Turecek,2008-11-15 13:42:51
Číslovka „dva“ je v 2.pádu (genitiv) a v 6.pádu (lokativ) stejná, totiž "dvou". Podle Slovníku spisovného jazyka českého se předložka „v“ pojí buďto se 6.pádem nebo se 4.pádem. Usoudil jsem, že by měla být shoda v pádu předložky „v“, číslovky „dva“ a podstatného jména „rok“. Proto jsem napsal "v letních obdobích posledních dvou rocích".
Předložka „do“ se podle stejného slovníku pojí s 2.pádem. Proto bych napsal „do dvou roků“. „V posledních dvou roků“ mě tahá za uši. Vás ne? Nebo vás tahá za uši „v posledních dvou rocích“? Když si ale na druh straně opakuji "v letních obdobích posledních dvou roků", tak mě to tak za uši netahá. Jenže v chytrých knihách jsou k tomu nějaké vyjádření nenašel. Třeba je znáte.
Pane Křepelko, myslím, že máte pravdu.
Karel Malý,2008-11-17 15:52:49
Dle mého názoru je vaše věta naprosto gramaticky správně, jen pan Tureček se ztratil v její větné stavbě. Aby měl pravdu, musel by do věty přidat ještě jednu předložku, pak by to znělo nějak takhle:"v letních obdobích v posledních dvou rocích", ale napsat "...v letních obdobích posledních dvou roků" je také správné a navíc to vypadá mnohem elegantněji.
Omluva
Pavel Táborský,2008-10-28 06:45:11
Omlouvám se, tenhle příspěvek měl být odpověď na příspěvek pana Turečka "Odpověď na "Pěkná shoda náhod""
Další obskurní grafy
Pavel Táborský,2008-10-28 06:43:50
OK, v tom případě bych si dovolil drze uvést odkazy na další obskurní grafy (ze stejného alarmistického zdroje). Data zjevně zfalšována a posléze prohlášena za vědecký konsenzus.
Takhle to podle alarmistů vypadalo posledních 400k let (nafitováno a asi upraveno ve photoshopu, aby to bylo konzistentní s hokejkovým grafem posledních století)
http://en.wikipedia.org/wiki/Image:Carbon_Dioxide_400kyr.png
A tady je vidět, jak zfalšovali klimatické modely, aby to vypadalo, že za zvyšování teploty můžou lidé
http://en.wikipedia.org/wiki/Image:Climate_Change_Attribution.png
blíží se normální standardní odchylce
Petr Skůpa,2008-10-27 17:17:27
1) Blíží se normální standardní odchylce, tedy v ní není.
2) Ani se jí tak moc neblíží (maximálně v brzky jarním období)
3) Až se takováto dispozice zopakuje několikrát, bude to zajímavé. Takto se to stejně dobře dá interpretovat jako statistické vybočení v rámci statistické odchylky od trendu zmenšujícího se zalednění.
4) Jestli se to bude opakovat...
když zimě zamrzne to co předchozí léto roztálo - pár decimetrů tlustým ledem, předpokládám, že v období kolem března to bude vykázáno jako "zaledněné" ? Zajímá mě rozsah v létě.
už tam je
Igor Turecek,2008-10-29 22:23:02
Rozsah zalednění (area zalednění) je již uvnitř standardní odchylky.
Pokud vás zajímá rozsah zalednění, tak jej můžete sledovat na http://arctic-roos.org/observations
Na * Arctic ice area and extent from SSMI (NERSC)
naleznete také graf, na který je odkázáno v mém článku. Je zde také vysvětlení co je area zelednění a co je extenze zalednění. Area zalednění je přísnější kriterium.
Pod hlavičkou * Total sea ice area and ice extent from 1978 to 2007/2008 (NERSC)
Naleznete další grafy. Jeden z nich ukazuje trend poklesu zalednění od 1978. Na dalších jsou animace.
Sběr dat není jednoduchý. Získaná data jsou mnohdy sporná až vysloveně chybná. Informace k tomu naleznete na http://www.osel.cz/index.php?clanek=3315
V komentáři k jinému článku
http://www.osel.cz/index.php?clanek=3368
se někdo vyjádřil tak, že nejde o nic neobvyklého, že statistická data jsou vždy zašuměná chybami. Není tomu tak. Data nejsou zašuměná nějakými nepřestnostmi, nýbrž chybná. Meteorolog Watts již nashromáždil více než 60 případů jak se nemá měřit teplota. Zcela chybná data je nutno z měření vyloučit. Systematické chyby (např. změna nátěru meteorol. budky, ohřívání vnitřku budky instalovanou žárovkou nebo akumulátorem apod.) je nutno zohlednit. Vědci na univerzitách se o těchto změnách nedozvěděli a pracovali s chybnými údaji. Práce s opravenými údaji bude možná až teprve tehdy, až se prověří větší část meteorologických budek.
Pak budou teploty naměřené pozemními stanicemi korigovány znovu. Na všechny údaje se nelze spoléhat.
Tajemné mizení meteorologických budek
Igor Turecek,2008-10-29 22:54:08
Kdyxž jsem psal článek
http://www.osel.cz/index.php?clanek=3368
tak jsem ve Wattsově databázi našel také jeden případ zmizení meteorologické budky, která se nacházela u parkoviště. Autor popisu budky napsal, že jednoho dne přišli nějací lidé a budku odmontovali. Jiná budka byla přenesena o několik stovek metrů do uzavřeného pozemku a stala se veřejně nepřístupnou. Některé budky se nacházely úplně někde jinde než na umístění odkazovala dosavadní databáze. Peníze (granty) na aktualizaci stavu meteorol. budek nebyly, takže američtí meteorologové jsou Wattsovi za jeho práci vděčni. Snad se někdy dozvíme jak to bylo s manipulacemi budek a s potěmkinovskými budkami.
To Elek Oskar
Tomas Habala,2008-10-27 16:54:04
Zdvyhnut ma byt zdvihnut, nerozumiem na co bolo dobre tam davat tuto chybu. Nie som si inak isty s tou zavislostou, ze ak je jeden rok malo more zaladnene, moze byt na buduci rok zaladnene len o kusok viac. V malych vzdialenostiach to moze hrat velku rolu, ale vo vzdialenostiach 100 viek km asi nie. Lad sa na hladine utvori bez ohladu na to, co okraj celorocnej ladovej kryhy je daleko 100 alebo 200 km, ak su na to vhodne teplotne podmienky. Ladova kryha nerastie postupne, ale na mori sa vytvaraju mensie kryhy a tie sa spajaju.
A co třeba fakta?
Pavel Táborský,2008-10-25 22:29:33
Možná je nejlepší podívat se na ty, kdo tání ledovců využívají k vydělávání peněz - rejdaře, kteří se snaží využívat námořní cesty Severním ledovým oceánem. Letos byla poprvé průjezdná severovýchodní (nad Ruskem) i severozápadní (nad Amerikou) cesta, poprvé po 125000 letech. Kolikanásobek směrodatné odchylky to představuje? :-)
http://en.wikipedia.org/wiki/Northern_Sea_Route#Ice-free_ports
Fakta a interpretace
Igor Turecek,2008-10-26 12:08:36
Za posledních několik desítek let průměrná teplota na Zeměkouli stoupla o několik desetin stupňů. Jenže alarmisté tento fakt dávají do souvislosti s průmyslovým rozvojem, zejména s nárůstem CO2. Ale nárůst CO2 není příčinou nárůstu teploty. Na Oslu bylo již mnohokráte uvedeno, že paleoklimatická fakta jsou jiná. Nejprve vzrostla teplota, pak vzrostlo množství CO2. CO2 je potravou pro rostliny, které tak působí jako puffer. Dalším velkým puffrem jsou oceány. Všechny příčiny nárůstu teploty nejsou známy. Hovoří se o mnoha teplotních cyklech planety, jež ve svém důsledku za spoluúčasti Slunce a jiných kosmických jevů ústí v nějaké teplotě na Zemi. Průmyslová činnosti to ale není. V dávných dobách bylo na Zemi mnohem tepleji a bylo zde mnohem více CO2 než dnes. Dvě fakta, totiž 1. nárůst teploty předcházel nárustu CO2; 2. před milióny lety bylo mnohem více CO2 než dnes a žádný průmysl nebyl, by musela stačit na odmítnutí hypotézy, že příčinou oteplení je CO2, který vzniká v důsledku ůdajné "nadměrné" průmyslové činnosti. Není tomu ale tak. Lidé raději věří sebemrskačům, profétům atd. Je zde ještě jiný faktor. A tentokrát opravdu lidský. Totiž přání, aby se nárůst teploty takto interpretoval. To je pak problém siociálně-psychologický, který s přírodními fakty nesouvisí.
Pěkná shoda náhod
Pavel Táborský,2008-10-27 07:07:52
Takže alarmisté se pletou i v tom, že nárůst atmosférického CO2 o 100 ppm za 200 let souvisí s průmyslem? Je jasné, že koncentrace CO2 se měnila vždycky, ale bylo to takhle rychle? A ta podobnost s vývojem množství spalovaných fosilních paliv je jenom náhoda?
http://en.wikipedia.org/wiki/Image:Carbon_History_and_Flux_Rev.png
Takováhle silná slova bych nečekal ani od pana profesora z Hradu. :-)
Celkem obdivuju Vaši jistotu. Působí to velmi vědecky. :-o
Odpověď na "Pěkná shoda náhod"
Igor Turecek,2008-10-27 15:42:50
Vámi uvedené grafy se evidentně vztahují na zprávu IPCC 2001. Data v této zprávě právníci z IPCC převzali od chemika Charlese Keelinga. Vezměte prosím v úvaha, že Keelingovy údaje pocházejí z jednoho jediného místa na Zeměkouli, Hawaie, observatoř Mauna Loa (http://www.mlo.noaa.gov/home.html), kde sopky neustále něco chrlí (http://plachy.blog.idnes.cz/c/44129/Havajsky-denik-Den-7-Do-pekla-a-zpet-vystup-na-Mauna-Loa.html)
Keeling ve svém článku (1986) o předindustriální koncentraci CO2 chybně citoval Reiseta (1872/1873). Zda to bylo úmyslně nebo omylem nevím. Každopádně data byla uměle selektována. Keelingův citovaný údaj – roční průměrná koncetrace CO2 okolo roku 1880 v nekontaminovaném prostředí má být 292 ppm (± 2ppm) - je chybný. Proč? Chemická metoda určení koncentrace CO2, používaná Reisetem, má metodický nedostatek v tom, že kyselina sírová absorbuje 20 ppm CO2. Metoda sama tedy snižuje skutečnou koncentraci. Opravený údaj předindustriální koncentrace CO2 na pobřeží Francie (tedy také z jednoho jediného místa) je tedy 312 ppm ± 3 %.
Reiset měřil koncentraci na severu Francie v Deppe na pobřeží Atlantiku, kde daleko široko žádná sopka není. Na rozdíl od Hawaie. Ale není to jenom prostředí. Data z Mauna Loa jsou zatížena systematickými chybami, jak zjistili Bate et al. 1969, Bischof 1977, Arlelli et al. 1999.
IPCC opakuje stará data se systematickými chybami jako kolovrátek. A po něm všichni novináři, politici, právníci a také někteří čtenáři Osla. Čtěte Osla pravidelně a také starší články. Tady se alespoň něco dozvíte ze skutečné vědy. Citovat obskurní údaje z Wikipedie (a veřejně se prezentovat jako já Pavel Táborský uvádím spolehlivé údaje) v době internetu a tedy možnosti údaje dohledat je – jednoduše řečeno – drzost. Obrázky na Wikipedii, na které odkazujete a o nichž tvrdíte, že to jsou data, vám za dvě hodiny photoshopem také namaluji. Když to přeženu, tak s koncentrací CO2 to máte jako s mraky. Foukne vítr a máte po koncentraci. A to jsem se ještě nerozepsal o posunovacím zákonu Wilhelma Wiena. Přečtěte si o tom něco. A je to také v jedné diskusi na Oslu – bohužel už nevím kde, musel bych to hledat.
Vy si ani možná neuvědomujete jaký je to všechno nesmysl. V 3000 molekulách vzduchu je jediná molekula CO2!
Kdybych se rozepsal o věrohodných údajích, tak by z toho nakonec byl článek. Ale shrnu to:
střední koncentrace CO2 byla v 19. stol. 321 ppm, ve 20. stol 341 ppm. S údaji od IPCC si tak akorát můžete – víte co. Nevíte? Vytapetovat stěny v pokoji. Arrhenius, Callendar a Keeling pracovali s chybnými údaji a došli proto k chybným závěrům.
Eric From, Cahrles D. Keeling: Reassessment of late 19th century atmospheric carbon dioxide variations in the air of western Europe and the British Isles based on an unpublished analysis of contemporary air masses by G.S.Callendar, 1986.
čemu a komu věřit
Pekny Brumla2,2008-10-28 10:57:53
Vážený pane Turečku, Osla čtu, že existuje Wienův zákon mě nepřekvapuje ani nikoho jiného, je znám přes 100 let. Umístění stanice na Hawaji je kvůli relativně nejmenšímu vlivu průmyslových emisí. Vaše argumenty jsou skutečně přehnané - foukne vítr a koncentrace není. Právě proudění vzduchu a velká rychlost molekul (hlavní složky vzduchu kolem 500 m/s) způsobuje poměrně dokonalé promíchávání vzduchu, měří se denně, takže náhodné vlivy jistě, doloženy jsou i vlivy sluneční činnosti.
Váš hlavní problém, zda je prvotní vliv teploty a pak CO2 ( následně oteplení uvolní CH4 z permafrostu, že?) nebo naopak- je to problém komplexní, teplota a vzestup CO2 ( který lze poněkud omezit) jsou spolu provázané a kumulativní. Takže je skoro jedno, co je původní- podvod je se tím nezabývat, což tak nějak nabízíte v článku.
Pokuste se odpovědět na mou otázku z počátku diskuze- proč píšete, že je v Arktidě 7 metrů ledu, když je tloušťka ledu 3 m. To je snadno porovnatelné jako vstup k věrohodnosti tohotočlánku.
oprava- smerodatna odchylka
Pekny Brumla2,2008-10-25 10:02:53
Oprava předchozího příkladu, kdy 9 krát je bota č.2 a jednou 12, průměr =3, směrodatná odchylka =odmocnina z (9+81)/10= odmocnina z 9 =3. Čili směrodatná odchylka je =3.
průměrná tloušťka ledu je 3 m
Pekny Brumla2,2008-10-25 09:24:13
Průměrná tloušťka ledu není dnes 7 m, to bylo 7 m, dnes je průměrná tloušťka ledu 3 m. To je rozhodující, nejde o hysterii, ale o úbytek ledu. Loňský propad ledu způsobil, že letošní zpětný nárůst ledu je jednoletý. Jednoletý led má menší životnost, rozlamuje se. Kritický je úbytek víceletého ledu. Kdo si chce něco přečíst o ledu v Arktidě, tak na http://gnosis9.net se tato problematika sleduje dlouhodobě, včetně mnoha grafů.
Směrodatnou odchylku najdeme třeba na http://smerodatna-odchylka.navajo.cz/
sigma = odmocnina z {(1/N(Xi-Xpůměr)^2}.
Kydž laické vysvětlení , tak příklad: V mateřské školce v jednom oddělení má 10 dětí boty všechny č.3, průměr =3, směrodatná odchylka=0. Ve druhém oddělení mají 9 krát č.2 a zapoměl tam boty Jan Koller č. 12. Součet taky =30 průměr = 3, sněrodatná odchylka = odmocnina z ((9*1*1+1*9*9)/10)= odmocnina z 0,9 = 0,95.
A právě takovou velkou odchylku představuje loňský propad. Loňský led se plošně zacelil, ale je tenký. Takže obavy o led jsou na místě, stejně jako o smysl tohoto "protipoplašného" článku.
A este raz statistika (a trochu lingvistika)
Elek Oskar,2008-10-25 02:00:51
Zdravim prispievatelov Osla.
Najskor male zabrdnutie do gramatickej spravnosti clankov. Pani Krepelka a Vomacka, bezpochyby ste na seba hrdi za dokonale zvladnutie ceskeho jazyka na zakladnej skole, ale majte na pamati, ze sa nachadzate na popularno-vedeckom serveri o prirodnych vedach, a nie na lingvistickom fore. Na takychto je podla mojho nazoru vysokou prioritou, aby clanok bol relevantny k teme, na ktoru jeho autor reaguje a za predpokladu, ze je jeho text pochopitelny a spravny, sa obcasna gramaticka chyba ma tolerovat, ak vyrazne nebrani kontinualnej cetbe clanku a jeho naslednemu pochopeniu. Osobne som pochopil, co autor myslel slovom "standartni" - Vy snad nie? Napadlo Vas vobec niekedy, ze autora moze tlacit termin odovzdania clanku, alebo ma jednoducho na praci nieco plodnejsie, ako si tri razy po sebe precitat clanok kvoli jedincom ako Vy? Ano, matematika je sice exaktna veda aj v otazke nazvoslovia, ale skuste si niekedy otvorit vysokoskolsku ucebnicu matematickej analyzy a schvalne, kolko ucelenych viet najdete vo formulaciach definicii, viet a dokazov? ;)
A teraz nieco ku statistike. Pan Poslusny, nakolko rozumiete pravdepodobnosti a statistike? Ja to nie som schopny z Vasho prispevku posudit, pretoze okrem premudrelej poznamky ste v nom nic skutocne mudreho svetu neprezentoval. Naopak, musim skonstatovat, ze pan Turecek, ak je laik, statistike rozumie pomerne dobre. Mohol sice uviest, ze sa jedna o trojnasobok standartnej odchylky, alias rozptylu, normalneho Gaussovskeho rozdelenia, ale to su len terminy a podstatu v svojom clanku vystihol dobre. Dokonca aj hodnoty distribucnej funkcie ma po nasobkoch rozptylu korektne na 2 desatinne miesta.
Problemom takehoto priamociareho aplikovania statistiky je podla mna nieco celkom ine, a totiz ze normalne pravdepodobnostne rozdelenie (N(0,1) a jeho linearne kombinacie (jeho parametrov)) popisuje hustotu pravdepodobnosti uskutocnenia nahodnych dejov, teda takych, ktore su navzajom nekorelovane. To je dost dolezite a podla mna by bolo potrebne prihliadat k tomu, ze rozloha Arktickej ladovej pokryvky v jednotlivych rokoch sa neda chapat ako jednotlive realizacie urciteho nahodneho javu, pretoze navzajom suvisia - ak v roku 2007 bolo podkriticke mnozstvo ladu, tak v nasledujucom roku sa ani za vynimocne chladnych teplot po cely rok nemoze zdvyhnut mnozstvo ladu nad dlhodoby priemer, aj ked statistika to v takejto aplikacii v podstate pripusta. Moje znalosti v tomto obore zial nestacia na to, aby som tu uviedol konecne a spravne riesenie tohto problemu, ale ak by som si mal tipnut, tak v tom budu nejaku rolu zohravat Markovske retazce.
Tolko teda moj prispevok do diskusie. Budem rad, ak mi niekto kompetentnejsi tematiku osvetli viac v podobe riesenia, ktore som sam nebol schopny sformulovat.
Uloha pre lokalne korektorky gramatickej spravnosti - do mojho prispevku som ukryl jednu zamernu hrubku (a dufam, ze ziadne nechcene ;) - som teda zvedavy, kto z Vas ju v mojom (slovenskom) prispevku najde.
Opet statistika
Michal Masin,2008-10-24 17:45:44
Ze by Gauss? Ale myslite, ze vam statiska pomuze, kdyz operujete se spatnou logikou? To muzete scitat a mocnit do aleluja. Nebo si myslite, ze kazdorocne odtava 7 metrova vrstva? Porad operujete s rozlohou ledu. Jenze potiz je v tom, ze ona jeho vrstva je stale tenci, coz je duvod stale vetsich letnich vykyvu. Ja myslim, ze lednimu medvedovi je statistika uplne fuk, pro nej je podstatne, jestli se behem letniho tani utopi nebo ne.
Směrodatná odchylka
Igor Turecek,2008-10-24 17:08:25
Vymysleme si, že průměrný měsíční plat je v České republice 23000.- Kč. Někdo bere 100000.-, někdo 6000.- Průměrný plat je iluzorní hodnota. Asi jako když někdo dá hlavu do mrazničky a nohy do trouby a bude tvrdit, že je mu příjemně. Nebo když si někdo dá dva obědy a ten druhý jen kouká, tak se statisticky najedli oba. A navíc sytý hladovému nevěří, že neměl nic k obědu. Průměr sám o sobě je nesmyslný a takové noviny, článek nebo knihu jednoduše vyhoďte, poněvadž jsou k ničemu.
Statistici vymysleli další ukazatele, které mají nějakým způsobem popsat realitu. Kromě průměru je to ještě odchylka od průměru nebo-li rozptyl. Rozptyl se táhne celou statistikou jako červená niť. Mezi ukazatele rozptylu patří také směrodatná odchylka. Jak se vypočte? Ve skupině A pracují tři lidé. Jeden 7, druhý 8 a třetí 9 hodin. Průměrně pracuje skupina 8 hodin. Ve skupině B pracuje první 1 hodinu, druhý 10 a třetí 13. Ten s jednou hodinou práce vydělává pochopitelně oněch 100000.-
Také skupina B pracuje průměrně 8 hodin. Jaký je rozptyl hodin?
Skupina A:
ten se 7 hodinama pracuje o 1 hodinu méně,
ten s 8 hodinama má odchylku 0
ten s 9 hodinami pracuje o hodinu déle.
Skupina B:
1 – 8 = -7
10 – 8 = 2
13 – 8 = 5
Tím jsme spočetli odchylky od průměru. Nemůžeme ale odečítat švestky od těsta, poněvadž jíme obojí, i když je těsto od středu švestkového knedlíku dále. Všechna čísla umocníme proto na druhou a tím se zbavíme záporných čísel a zároveň si lépe uvědomíme, že některá čísla leží od středu skutečně mnohem dále než jiná.
Skupina A:
odchylka ...... druhá mocnina odchylky
-1 ...................1
0.....................0
1.....................1
součet ............2
Skupina B:
odchylka.........druhá mocnina odchylky
-7.................49
2....................4
5..................25
součet..........78
Oba součty jsou velmi rozdílné. A byly by ještě větší, kdyby skupiny byly početnější a rozptyl také větší. Statistici zase proto kouzlí a součet dělí počtem lidí ve skupině a říkají tomu variance (nebo-li rozptyl). Skupina A: 2 / 3 = 0,67 Skupina B: 78 / 3 = 26
Vzhledem k tomu, že jsme čísla předtím umocňovali, musíme operace vyrušit a budeme odmocňovat. Druhá odmocnina z 0,67 je přibližně 0,82; druhá odmocnina z 26 je přibližně 5,1.
Závěr: Skupina A pracovala v průměru 8 hodiny a také každý člen skupiny pracoval v průměru 8 hodin s rozptylem mezi 7 až 9 hodinami. Skupina B pracovala také v průměru 8 hodiny, ale ne každý člen skupiny. Někteří jen 3 hodiny, jiní až 13 hodin. Vypočítaný průměr 8 hodin tedy skupinu B vůbec necharakterizuje a pravděpodobně byli dáni dohromady jedinci, kteří patří do úplně odlišných skupin. Skupinu B musíme tedy znovu rozdělit a znovu počítat průměr a směrodatnou odchylku. Pokud má skupina B 10000 jedinců, provádíme výpočty a rozdělení tak dlouho, až dostanem skupiny, které lze aritmetickým průměrem charakterizovat.
Aritmetický průměr a směrodatná odchylka nám tedy velmi rychle prozradí sourodost nebo nesourodost statistického souboru. Použijme třeba roční a měsíční průměry rozsahu zalednění. Můžeme pak zjistit, jak se měsíční průměry odchylují (jaký mají rozptyl) od ročního průměru. Lze také počítat rozptyl oproti ročnímu průměru z denních 365 průměrů a ty zase mohou být průměrem ze dvou měření za den. Nebo i více měření. Výsledek by byl ale v podstatě vždy stejný. Velký rozptyl pro jednu skupinu dat a malý pro druhou. A to právě tehdy, kdybychom ve skupině B porovnávali rozsah zalednění v měsících, které k sobě nepatří. To jest, dali bychom dohromady leden s červencem a únor se srpnem, zatímco ve skupině A březen s dubnem a květen s červnem.
William Sealy Gosset pracoval začátkem 20. století jako chemik v anglickém pivovaru Guinness. Vymyslel postup jak posuzovat malé vzorky piva. Firma by mu ale nedovolila jeho vědecké práce publikovat pod svým jménem. Možná, že by ho i na hodinu vyhodili z práce. Uveřejňoval proto pod pseudonymem. Ví někdo jak to souvisí se směrodatnou odchylkou, rozptylem, výběrem vzorku a rozdělením hodnot? Jak se jmenuje rozdělení, které vymyslel?
to je fakt komicke,
Zdena Galajdova1,2008-10-24 14:58:43
autor informuje o ledove pokryvce polu a panove se tady rozciluji nad gramatikou, mimochodem stejne spornou :-)))) Takove hnidopisstvi svedci o snaze za kazdou cenu neco spatneho najit.... jak ubohe.....
Pane Turečku,
Jan Poslušný,2008-10-24 11:09:15
pište prosím, o tom, čemu rozumíte - statistika to ale rozhodně není. Děláte tím těm zmiňovaným laikům medvědí službu.
standardní odchylka
Jaromir Krepelka,2008-10-24 10:27:05
Především se jedná o standardní odchylku (od standard), nikoliv standartní (pocházející od slova standarta), rovněž autor volně zaměňuje normálnost (od normální) s normalitou (od normy). První věta - po opravě "Rozloha arktického ledu se blíží normální standardní odchylce" - je logický nesmysl, zřejmě se jedná o odchylku rozlohy ledu od jeho průměrné rozlohy zjištěné průměrováním pro určitý časový úsek roku (podle tvaru grafu pravděpodobně dekádu, nikoliv měsíc, jak uvádí popiska) přes posledních 28 let. I když závěr o nevybočování z normálnosti se může v budoucnu ukázat jako správný, přesto je hodné pozornosti patrné zmenšení rozlohy ledu v letních obdobích posledních dvou roků.
Pane Turečku
Xavier Vomáčka,2008-10-24 13:41:25
Standartní odchylka je max. odchylka vlajky prezidentské standarty od fangle. Slovo standardní je od slova standard. Slovo standartní je opravdu od slova standarta. Jestli nám nevěříte zeptejte se např. na jazykové poradně Ústavu pro jazyk český při Akademii věd ČR, zde: http://www.ujc.cas.cz/oddeleni/index.php?page=poradna
chyba ve skloňování
Igor Turecek,2008-10-24 13:41:39
Spisovně správně se píše "posledních dvou rocích" a nikoliv "roků"
Norma atd.
Igor Turecek,2008-10-24 14:27:52
Vámi uvedené souvislosti a odvození normality od normy a odvozením normálnosti od normální jsem ve Slovníku spisovného jazyka českého nenalezl. Slovník praví:
Heslo norma: 1. pravidlo ... atd.; 2. normální stav, obvyklost, normálnost.
Heslo normální: 1. vyskytující se za běžných ... okolností; 2. představující normu ...; 3. stanovený normou ...; 4. mající směr normály.
Uveďte prosím zdroj, z něhož čerpáte.
Statisticke hratky
Michal Masin,2008-10-24 10:20:49
Prave proto, ze se autor nazyva laikem, nemel by mozna zjednodusovat. Ve svem prispevku mluvi a statisticky dokazuje pouze odchylky v sezonnim cyklu zaledneni, co se tyka do plochy. Grafy vsak jiz nehovori o sile ledu. Pokud pouzijeme selsky rozum, tak zrejme odvodime, ze vykyv v plose zaledneni behem letnich mesicu je zpusoben tim, ze roztava slabsi vrstva ledu. Tataz logika rika, ze pres zimu muze zamrznout dokonce i vetsi plocha more, ale slabsi ledovou krustou. Pokud to zprumerujeme, tak nam statisticky hezky vyjde, ze zaledneni je stale stejne. Jinak se nedomnivam, ze to co vykazuji grafy pro letni mesice se blizi standartni odchylce. Dle meho mineni jsou tyto hodnoty od sede zony pomerne dost daleko.
Přílišné zjednodušení.
Ladislav šimeček,2008-10-24 07:05:37
Autor se snaží zjednodušovat i pro ty, co statistiku neznají.Což lze chápat a s povděkem kvitovat. Ale zdá se, že při zjednodušování zaměnil odchylku naměřené hodnoty od průměru za naměřenou hodnotu. Tady už je zjednodušení takové, že přestává mít smysl a stává se protismyslem.
Nemáte taky ten dojem?
Láďa
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce



