Téměř každý již slyšel o kvantových počítačích a co všechno nezvládnou (a že se často dočtete věci!), ale popravdě od revolučního Shorova algoritmu pro prvočíselný rozklad z roku 1994 se toho zas tak moc neudálo. Abychom nebyli nespravedliví, děje se tam toho celkem dost ale rozhodně ne tak senzačního v porovnání s tímto algoritmem. Oproti tomu kvantová teorie komunikace pokročila v posledních letech nebývalým tempem a o objevy není nouze. Korunu tomu zcela určitě nasadili G. Smith (IBM) and J. Yard (Los Alamos) právě vyšlým preprintem. Abychom ocenili tento nový výsledek, je třeba se vrátit do klasické teorie informace. Jak asi víte, její základy položil C. Shannon a jedním z jeho velkých výsledků byla definice a výpočet kapacity komunikačního kanálu. Kapacita (ztrátového) komunikačního kanálu je počet bitů, které lze přenést tak, aby chyba na straně přijemce bylo libovolně malá (v asymtotickém režimu samozřejmě). Intuitivně je jasné, že pokud výstup z kanálu je jen nepatrně korelován se vstupem, kapacita bude nenulová. I v případě, že máte opravdu špatné mobilní spojení a neslyšíte, co vám někdo na druhem konci říká, stačí použít jednu opravdu hloupou strategii, tj. zopakovat zprávu několikrát, abyste s vysokou pravděpodobností získali zprávu celou. Naopak, pro kompletně náhodný kanál nelze přenést nic, ani když vám druhá strana zprávu opakuje stokrát a dá se ukázat, že v principu neexistuje žádné sofistikované kódování pro tento případ. Kapacita klasického kanálu je totiž aditivní. To znamená, že kapacita se sčítá pro simultánní přístup ke dvěma (nebo více) stejným (různým) kanálům. Takže v případě náhodného klasického kanálu 0+0 = 0 a je vymalováno.

Jak už naznačuje přítomnost adjektiva klasický, zaměříme se na nyní na kvantové kanály. Předně, pokud máte kvantový kanál, můžete si vybrat, zda chcete poslat klasickou (bity) nebo kvantovou informaci (qubity). První případ se nezdá příliš moudrý, uvážíme-li, že kvantový kanál je z principu ztrátový, tak proč si komplikovat život? Avšak (odhodíme-li celou krásu tohoto konceptu a zaměříme se na praktickou stránku) výhody značně předčí nevýhody. Kvantová distribuce klíče (QKD)  toho budiž dokladem. Tam je klasická informace (klíč) přenášena po kvantovém kanálu a bezpečnost QKD je něco, co klasická kryptografie může jen tiše závidět. Poznamenejme, že otázka aditivity klasické kapacity kvantového kanálu je slavný a stále otevřený problém kvatové teorie informace.
Nás ale v souvislosti s uveřejněným preprintem zajímá plně kvantový případ - tedy kvantová kapacita kvantového kanálu. Kapacitou zde rozumíme počet přenesených qubitů tak, aby se daly na výstupu téměř perfektně zrekonstruovat (opět asymptoticky). Autoři výše uvedeného článku ukázali případ, kdy simultánní užití dvou kanálů s nulovou kapacitou dá vznik kanálu s nenulovou kapacitou (pokud nevíte, kdy udělat Wow! tak teď je ta pravá chvíle). Máte-li tak dva kvantové telefony s kterými se nikam nikdy nedovoláte a použijete je společně, dostanete najednou telefon, s kterým se někam dovoláte. To už je pěkně bizarní. Jak se k tomu dostaneme?

Na začátku stojí objev od polského rodinného klanu Horodeckých, kteří na svých výpravách do království operátorových algeber popsali poněkud zvláštní druh entanglementu nazvaný bound entanglement (vázaný entanglement?). Ten je zajímavý tím, že pokud máte stav s touto vlastností, tak technicky je to entanglovaný stav (tedy neklasicky korelovaný), ale ten entanglement z něj nejde za normálních okolností dostat (proto vázaný). Dále platí, že každý sdílený kvantově provázaný stav může v principu sloužit k vytvoření kvantového kanálu. Kanál ustanovený z vázaného entanglovaného stavu (říkejme tomu Horodecki kanál) má však nulovou kvantovou kapacitu. Jinými slovy, pokud jej dvě vzdálené laboratoře sdílí, nelze jej použít pro žádný v současnosti známý ryze kvantový komunikační protokol (narozdíl od sdíleného maximálně entanglovaného stavu, který se hodí kupříkladu na kvantovou teleportaci). Slovo kvantový v předchozí větě je klíčové, neboť překvapivě vázané entanglované stavy lze použít k privátnímu sdílení klasické informace (klasická privátní kapacita je nenulová). Pokud nyní vezmeme jiný kanál s nulovou kvantovou kapacitou, např. erasure channel (vymazávací kanál), který s 50% pravděpodobností ponechá kvantový stav netknutý a s 50% jej zahodí, a paralelně jej jistým způsobem užijeme s Horodecki kanálem, dostaneme nenulovou kvantovou kapacitu

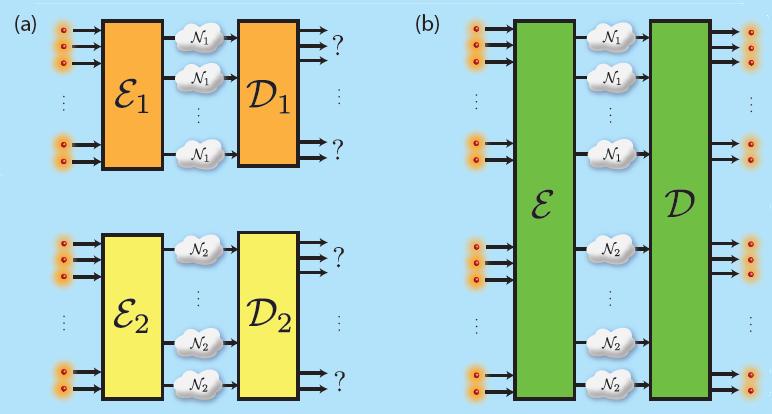
E_i je kódovací operace, která připraví kolektivní kvantový stav, aby mohl být přenesen kvantovým kanálem. Dekódovací transformace D_i na straně příjemce obnoví zaslanou informaci. Pokud mají dva kanály N₁, N₂  nulovou kvantovou kapacitou žádná taková dvojice D/E neexistuje. (b) Užijeme-li je souběžně dva kanály s nulovou kvantovou kapacitou, existuje překvapivě možnost, kdy je kapacita nenulová.

Na závěr můžeme shrnout, že kvantová kapacita není aditivní. Je celkem možné, že bude třeba přehodnotit současné paradigma, že kapacita plně vystihuje komunikační schopnosti (kvantového!) kanálu.