To, co je uvedeno vpředchozí větě ale, jako většina jistých faktů, není za jistých okolností pravda (a to přeskočíme problémy s neodporující si definicí identických částic, které se také moc neřeší). Zrekapitulujme si nejprve, jaký typ argumentu vede na známou odpověď a co je na ní nedobře. Kořeny rozdílného chování fermionů a bosonů leží v topologii prostoru kolem nás.
Topologie je disciplína studujíci operace na matematických objektech, kdy dovolíme jakoukoliv elastickou transformaci, ale nesmíme daný objekt přetrhnout, propíchnout nebo něco na něj přilepit (topologům jistě vstávají vlasy hrůzou na hlavě). Nebudu opakovat profláknutý vtip o tom, jak je pro topology nemožné rozlišit objekty každodenní potřeby a raději uskutečníme následující experiment.
Zavedeme souřadný kartézský systém (o dimenzi rovné třem) s dvěma částicemi (pro jednoduchost), kde jejich poloha je určena dvěma různými vektory. Protože jsme v kvantovém světě, jsou naše částice vlastně kvantovými stavy v jisté reprezentaci. Nyní zapneme nějaké vnější pole s pomocí kterým obě částice vyměníme mezi sebou. Částice jsou nerozlišitelné, a proto neumíme rozlišit mezi rozdílem obou vektorů před a po výměně, a tak musíme obě možnosti ztotožnit. Navíc z našeho prostoru vyjmeme singulární bod odpovídající oběma částicím na stejném místě. To je poněkud obtížné si představit, neboť ono ztotožnění probíhá vlastně ve čtvrtém rozměru (ve třech dimenzích už jaksi není místo).
Tato struktura se jmenuje reálný projektivní 2-prostor RP2 a je velmi blízce spjatá s grupou rotací ve třech dimenzích známou jako SO(3). Konkrétně, jedná se o její grupový manifold, tedy něco jako prostor všech parametrů dané grupy (myslím, že se to ošklivě překládá jako varieta, nebudeme se přít o překlady v tomto příspěvku, to prostě není důležité mít za každou cenu českou verzi) a lze si jej přeci jen trochu představit, pokud se zamyslíme nad obrázkem:
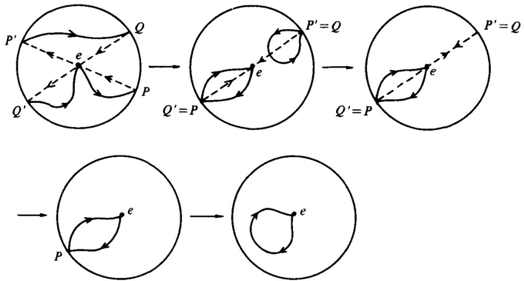
Pokud se z centra vydáme do bodu Q´, který je ztotožněný s protilehlým bodem Q a vrátíme se zpět do počátku, nemůžeme výslednou křivku stáhnout do bodu (pokud se pohne Q´, pohne se i Q podle definice). Ale můžme vyrazit k povrchu ještě jednou do bodu P´ a vrátit se z bodu P do počátku. Takové dva oběhy jsou už topologicky ekvivalentní jednoduše souvislé křivce.
Ačkoliv by rotace v našem známém třídimenzionálním prostoru neměla být problém uchopit, globální struktura SO(3) je netriviální. Však se přesvědčme sami. Pokud se na manifoldu vydáte z centra, v okamžiku kdy protnete povrch, ocitnete se najednou na druhé straně. O co hůř, pokud se vrátíte do počátečního odkud jste vyšli, není to to samé, jako se nikam ze začátku nehnout. Tedy ta trajektorie, kterou jste ušli, se nedá „stáhnout“ do bodu.
Ale můžete udělat něco jiného: ujděte tu samou cestu ještě jednou a najednou je to ekvivalentní jako byste nikam vůbec nešli. Jinými slovy, SO(3) má dva druhy cest, které se nedají spojitě transformovat jedna do druhé (řekne se, že SO(3) je dvojitě souvislá, její první homotopická grupa je izomorfní s Z2 (cyklická abelovská grupa řádu dva) a abyste sejmuli tuhle zábavnou degeneraci, musíte se poohlédnout po její pokrývací grupě SU(2)). Nyní zpět k bosonům a fermionům. Z předchozích úvah přirozeně plynoucím požadavkem, aby po dvou výměnách byl stav obou částic nerozlišitelný (dva oběhy = žádný oběh), nám vyjde, že stav po jednom oběhu může zůstat nezměněný anebo získá fázový posuv mínus jedna![]()
a právě toto předpovídá existenci dvou rodin částic – bosonů a fermionů. Připomeňme, že se jedná se o tzv. topologickou fázi, kde nezáleží na detailech cesty ale jenom na typu cesty. Z pohledu teorie grup bosony odpovídají symetrické jednorozměrné reprezentaci grupy permutací a fermiony antisymetrické reprezentaci. Zjevně se jedná o celkem jednoduché reprezentace.
Nemohli jsme si ale celý ten topologický cirkus odpustit a prostě to mínus spočítat, jak se to obvykle dělá? No právě nemohli, protože bychom se připravili o něco velmi zajímavého. Představte si, že tu samou proceduru se ztotožněním dvou vektorů a vyjmutím singularity uděláte ne ve třírozměrném, ale ve dvourozměrném světě. Intuice tvrdí, že to musí být čím dál tím jednodušší, ale opak je pravdou. Naštěstí si to ale teď už můžeme i lehce představit. Vystřihněte si kolečko z papíru, nakreslete si čáru reprezentující poloměr a nastřihňete kolečko podél té čáry. Složte si kornout tak, aby protilehlé body byly vzájemně u sebe. Získali jste reálný projektivní 1-prostor (RP1) velmi blízce spjatý s rotací na ploše. Ta je diktována grupou SO(2), která je co do popisu rotace opravdu jednoduchá, ale jinak topologicky pozoruhodná. Pokud vyjdete z daného bodu na okraji kornoutu, můžeme přijet zpátky dokonce nekonečně mnoha způsoby. Klíčovou roli hraje ona singularita znemozňující stáhnout smyčku do bodu a obecně, pokud obejdete singularitu n krát není to to samé jako obejít ji m krát. Je to názorná ilustrace nekonečné souvislosti grupy SO(2).
To má ovšem hluboký dopad na chování kvantových stavů na 2D (nezakřivených) plochách. Nyní už nelze obecně říci, jak se odlišná topologie SO(2) projeví na transformačních vlastnostech kvantových stavů a už vůbec není zřejmé, jakou statistikou se tyto částice budou řídit. Odtud pramení i jejich jméno – anyony – tedy jakákoliv statistika. Anyonová statistika ovšem není cíl našeho vyprávění, my se potřebujeme dostat ke kvantovému počítání, jak název naznačuje. Navíc ani zatím není zřejmé, zda se anyony realizují nějakým způsobem v přírodě (nebo alespoň v laboratoři), ale to až nakonec.
Stejně jako bosony a fermiony jsou reprezentovány grupou permutací, jsou i anyony reprezentovány jejím půvabným zobecněním známým jako braid group. Jak je asi zřejmé, když mezi sebou dva objekty prohodíte dvakrát (rozlišitelné nebo ne), dostanete výchozí stav. Ale u anyonů to, jak vidno, neplatí (díky topologickým vlastnostem SO(2)). Podívejme se na následující obrázek
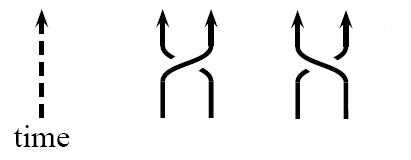
Dva anyony obíhající kolem sebe funkcí času. Díky vlastnostem grupy SO(2) (SO(2,1)) se navíc musí rozlišit oběh po a proti směru hodinových ručiček. To určuje znaménko pro winding number.
Máme dva anyony a budeme je otáčet kolem sebe, kdy úhel otočení je funkcí času. Dostaneme vlastně časoprostorový diagram, kde výsledné čáry jsou světočárami v časoprostorovém diagramu a mimochodem vyměnili jsme tak grupu SO(2) za SO(2,1) (dvě prostorové dimenze a jedna časová). V nejjednodušším případě je braid group reprezentována opět nějakým fázovým posuvem![]()
, kde theta je zatím nespecifikovaný úhel a n počet ovinutí (winding number). Bosony a fermiony získame ve speciálním případě, kdy ![]()
(pokud někomu klasický případ připadá jako konstrukce copů, jste na správné stopě).
Další pozoruhodný rozdíl mezi permutační a braid group je, že prvně jmenovaná grupa je konečná (N částic odpovídá N! permutacím, ale druhá grupa je nekonečná). Nyní vezměme tři anyony a nejprve otočme první kolem druhého a poté druhý kolem třetího. Zopakujme stejný experiment, ale nejprve otočme druhý kolem třetího a pak první kolem druhého.
Co dostaneme?

Stejný výsledek. Jinými slovy máme tu komutujíci (abelovské) anyony. Ale to nejlepší teprve přijde. Stejně jako grupa permutací má vícedimenzionální reprezentaci (podle všeho se v přírodě nerealizují), má i braid group vícedimenzionální reprezentace. V tom případě jsou rotace anyonů kolem sebe reprezentovány maticemi a ty obecně nekomutují (neabelovská reprezentace).
Tedy, v popsaném experimentu se třemi anyony budou výsledky navzájem odlišné. To je ovšem skvělá zpráva! Ví se totiž, že některé neabelovské reprezentace braid group tvoří hustou množinu (dense set) v SU(N), tj. grupě unitárních transformací. To znamená, že každou takovou transformaci lze „nasimulovat“ s prvky braid group s libovolnou přesností. A co to je vlastně kvantový počítač? Zjednodušeně řečeno, je to jedna velká unitární operace z grupy SU(N) nad N qubity (plus příprava kvantového stavu na začátku a nějaké to měření na konec). Shrnuto, prostým posouváním anyonů kolem sebe můžeme vesele kvantově počítat. Ale není to trochu přehnané zaplétat se s braid group, přeci jen na kvantových obvodech se, sice pomalu, ale přeci již pracuje? V tom je ale problém, pracuje se ale pomalu a jeden z hlavních problémů je nechtěná interakce s prostředím (dekoherence). Existují sice opravné kvantové algoritmy pro kvantové chyby, ale ty pracují až od jisté meze, kdy interakce s prostředím není příliš silná. Jinými slovy, současné kvantové platformy jsou nesmírně citlivé k lokálním poruchám. Ale to je přesně, co řeší topologické kvantové počítání. Vzpomeňte, že nezáleží po jaké cestě se jeden anyon otočí kolem druhého, stačí, když se otočí.
Topologický kvantový počítač je hluchý k chybám.
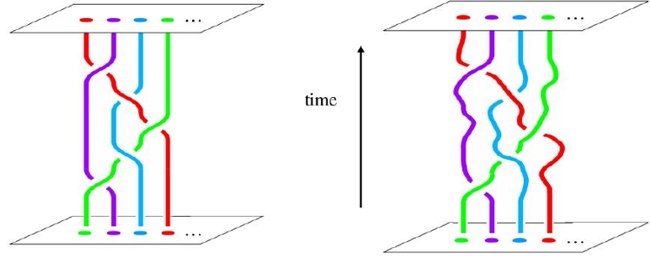
Braiding čtyř anyonů je šumu odolná transformace. Pro kvantové topologické výpočty je celkem jedno, pokud se nám třese ruka. Hlavně, abychom je prohodili.
Dají se neabelovské anyony přpravit v laboratoři? U abelovských se to už podařilo. Od osmdesátých let je studován kvantový Hallův jev v dvoudimenzionálních polovodičových strukturách, ve kterých je chycen elektronový „plyn“. Kvantový Hallův jev je dlážděn Nobelovými cenami (jednu dostal i tento „emergentní“ pán) a asi největším překvapením byl objev a vysvětlení zlomkového kvantového Hallova jevu (quantum fractional Hall effect). Elektrony ve 2D strukturách (a za nízkých teplot a vysokých magnetických polích) se chovají jakoby měly neceločíselný náboj. Je to pozoruhodný projev kolektivního chování jinak slušných částic (běžně se mluví o tzv. kvazičásticích), který nemá nic společného s kvarky. Experiment zhruba vypadá tak, že se na dvourozměrném vzorku měří závislost podélné a příčné vodivosti na příčném magnetickém poli a pozoruhodné jsou dvě věci:
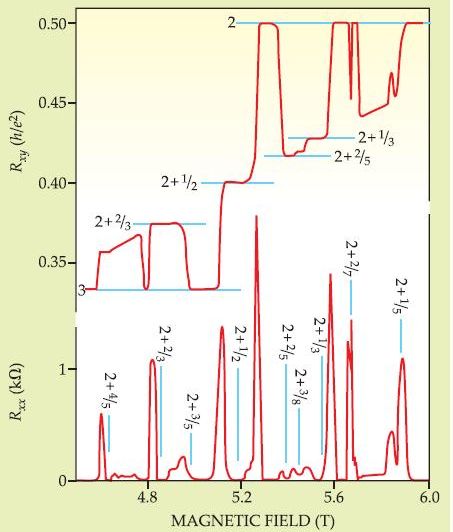
Závislost podélné a příčné rezistivity na magnetickém poli. Jak vidíme z horního grafu, nejenom je rezistivita kvantována, ale navíc poskakuje po neceločíselných násobcích.
Jednak vodivost (nebo rezistivita, jak chcete) se mění po skocích (zodpovědné za slovo kvantový), ale navíc to nejsou násobky jedné, jak by se čekalo od elektronů, ale po neceločíslených násobcích (zlomkový). Konkrétně, Hallova příčná vodivost má tvar
![]()
kde e je elektronový náboj, h Planckova konstanta a ν je obecně racionální číslo. Např. stavy
![]()
což je ten úhel z nejjednodušší (abelovské) reprezentace braid grupy. Právě stav s m = 3 se podařilo již v laboratoři připravit. Jak jsme ale naznačili, pro kvantové počty jsou nezbytné neabelovské anyony a nadějným kandidátem je stav s
![]()
Možná někdy příště si povíme, jak se qubity s anyony vlastně sestavují, nicméně jako ochutnávku jedno klíčové nelokální kvantové hradlo v braid group reprezentaci můžete vidět zde:
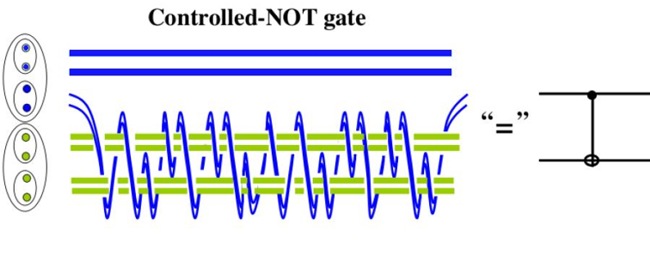
Jedno z klíčových hradel pro kvantové počty (CNOT) reprezentováno jako anyonic braiding. Jedná se o qubitovou bazi (modrá a zelená), kde každý qubit je reprezentovaný čtyřmi anyony.
Kviz na konec: Jaká společnost sleduje topologické kvantové počítání s velkým zájmem a je vlastníkem práv na US patent # 7250624?
Produkce těžkých antijader a antihyperjader
Autor: Vladimír Wagner (24.09.2024)
Tak nám zmizel nejjasnější signál exotické fyziky
Autor: Vladimír Wagner (08.08.2024)
Je za spontánními mutacemi DNA kvantová mechanika?
Autor: Stanislav Mihulka (09.05.2022)
Kvantoví mechanici poprvé kontrolovaně vystavěli kvantové doménové stěny
Autor: Stanislav Mihulka (20.02.2022)
Co opravdu říká supernova SN1987A k rychlosti světla
Autor: Vladimír Wagner (05.07.2014)
Diskuze:



