Co je informace?
Claude Elwood Shannon (1916 – 2001) byl jeden z těch, kdo vymýšlel dnešní informační technologii a je autorem bitu. Namísto jeho života představme spíše něco z jeho díla.
Představme si, že někdo sedí zády k šachovnici a otázkami má zjistit, kde se nachází jediná šachová figura – viz obrázek. Druhá osoba smí odpovídat pouze „ano“ nebo „ne“. Všechna pole mají stejnou pravděpodobnost, že se na ně osoba zeptá. Nuže, kolika otázkami lze takové pole na šachovnici zjistit? Určitě záleží na tom, jak se ptáme.

1. Nachází se takové pole v dolní polovině? (Ne)
2. Nachází se toto pole v levé polovině zbytku? (Ne)
3. Nachází se toto pole v dolní polovině zbývajících 16? (Ne)
4. Nachází se toto pole v levé části zbývajících 8? (Ano)
5. Nachází se toto pole v dolní části zbyvajících 4? (Ano)
6. Nachází se toto pole v levé části zbývajících 2? (Ne)

Zjištujeme, že je zapotřebí šest otázek, abychom jednoznačně určili jedno libovolné pole ze 64 stejně pravděpodobných. Jistě jste si všimli, že bychom se mohli také ptát, nachází-li se vpravo nebo v horní polovině. Výhodné je ve všech šesti otázkách vždy kombinace typu vlevo-dole nebo pouze typu vlevo-nahoře nebo jen vpravo-dole, atd. Ušetříme si tak namáhání buněk mozkových.

Při přechodu ke druhé otázce se kromě informace „pole se nachází v horní polovině“ předává také informace „pole se nenachází v dolní polovině“. Běžně obě odpovědi označujeme jako informace nebo obsah informace. Informatici chápou ale pod pojmem „informace“ něco jiného. Nikoliv kde se pěšec (objekt) nachází, nýbrž že byla zodpovězena jedna otázka s dvěmi možnostmi. Kuriózně označují tu skutečnosti, že byla zodpovězena jedna otázka pojmem „informační obsah“.
Matematicky se příklad se šachovnicí pojímá takto: Odpověď „ano“ nebo „ne“ se opakuje šestkrát. Tedy 2 x 2 x 2 x 2 x 2 x 2, nebo-li 2⁶ . Výsledkem této početní operace je číslo 64 nebo-li 64 = 2⁶. Označme počet všech polí šachovnice m (to jest počet všech stejně pravděpodobných možností) a počet otázek h (nebo-li rozsah potřebné informace). Obdržíme tak vztah m = 2^h. Převedením na logaritmus, poněvadž grafické zobrazení je pak lineární a ne exponenciální a ušetří se tak namáhání buněk mozkových, obdržíme h = log2 m. Pravděpodobnost p jednoho pole je 1/64, tj. p = 1/m, nebo-li m=1/p. Tím obdržíme h = log₂ 1/p = – log₂ p. Zjednodušme zápis duálního logaritmu log₂ na ld, ob-držíme h = – ld p. Navzdory znaménka mínus je výsledný rozsah informace pozitivní, poněvadž p je menší nebo rovno 1.
Namísto pojmu rozsah informace (information span) se pro proměnnou h ustálilo označení informační obsah (information content), což je zavádějící, poněvadž se nejedná o obsah v běžném slova smyslu. Vzpomínáme-li si dobře, je proměnná h počet otázek a nikoli obsah těchto otázek. Proč se o tom rozepisujeme? Čte-li totiž lékař, biolog nebo psycholog texty informatiků, může se pojmem informační obsah nechat lehce svést k tomu, že použije pojem informace neadekvátně na popis činnosti mozku. Mozek v žádném případě nezpracovává informační obsahy, nýbrž vzruchy a signály neurotransmitery, apod..

Zpracování informací
Zopakujme si, že informace v běžném slova smyslu je vždy nositelem významu. A to vědomého významu. Naproti tomu existují různé kvantitativní míry informace, které s vědomým významem nemají nic společného. Některé z nich si níže ukážeme. Pravda, lidé vytvářejí informace a zpracovávají informace například v úřadech, novinách, apod. Pracují se symboly. Ale mozek takto nepracuje. Mozek informace nezpracovává přímo, nýbrž zprostředkovaně přes vzruchy a neurotransmitery. Jak také jinak, že? Mozek zpracovává vzruchové struktury. Tyto vzruchové struktury jsou nejrůznějšího původu. Mohou pocházet ze smyslů, z nejrůznějších orgánů (jako například ze střeva viz http://www.osel.cz/index.php?clanek=2856) nebo mohou vznikat v mozku samotném.
Najde-li tedy čtenář v nějakém vědeckém pojednání obrat „zpracování informací mozkem“, může si být jist, že z 90ti procent autor neví o čem mluví. Slovo „informace“ je pak nutné důsledně nahradit slovem „vzruch“ a větu přečíst znovu. A ptát se, dává tato věta smysl? Důvod k tomuto rozlišení je ten, že informační technologie zpracovávají informaci na symbolické úrovni, zatímco biologické systémy na subsymbolické. Výrazem přání přiblížit se k této formě zpracování jsou například umělé neuronové sítě. V drtivém počtu případů se umělé neuronové sítě simulují na „symbolických počítačích“ a možná odtud pochází a je nadále utvrzována záměna symbolického a subsymbolického modelu.
Na následujícím obrázku si osvětlíme pojem zpracování informace ve smyslu výpočetní techniky. Použijeme k tomu známý fyziologický experiment I.P.Pavlova. Jestliže hladový pes uvidí jídlo, začne slintat. V Pavlovově experimentu se k jídlu přidalo světlo. Po určité době zácviku pes slintal při spatření světla.

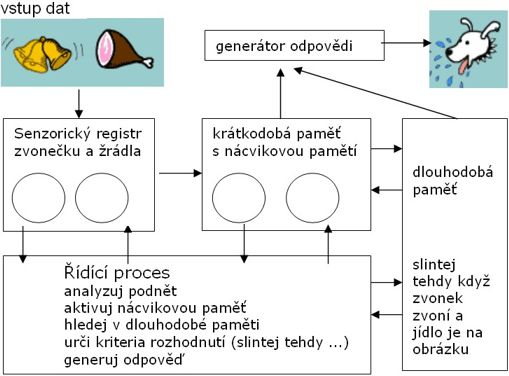
V blokovém schématu vidíme jak jsou vstupní informace o zvonečku (který zde nahrazuje světlo) a žrádle dále zpracovány a vedou ke slintání psa. Podobně analyticky se postupuje také při programování, ovšem ke strojovému kódu je to ještě daleko.

Kvantitativní míry informace a kódování

Příklad:
Jakou informační hodnotu v šachovém příkladě má otázka „Pole leží v horní
polovině?“ Nebo jinak: Jaký je informační rozsah otázky „Pole leží v horní polovině?“ Pravděpodobnost všech polí šachovnice je stejná. Je tedy lhostejné, jestli se znak „hledané pole“ vyskytuje v horní, dolní, levé nebo pravé polovině. Označme první osobu jako vysílač informací ano-ne, druhou jako přijímač. Tím je dán počet možností jak odpovědět: m = 2. Z toho plyne, že pravděpodobnost pozitivní odpovědi na první otázku je p = 0,5, poněvadž p = 1/m. Informační rozsah odpovědi ano-ne je h = – ld 0,5 = 1 bit. Bit je jednotka informace. Je to pojem vytvořený Shannonem ze slov „binary digit“. Stejně se postupuje i u dalších otázek. A poněvadž se zbytek šachovnice vždy rozdělí na dvě stejné poloviny, je také pravděpodobnost vždy rovna p = 0,5. Sečteme-li informační rozsah všech otázek, obdržíme hodnotu 6 bitů. (Výpočet logaritmu dualis ld x = log x / log 2 = ln x / ln 2)

Příklad:
Podobně bychom postupovali i v případě mince, která má rub a líc nebo pannu a hlava. Pochopitelně, že mince není žádný vysílač informací, stačí ale, když určité informace pozorujeme. Počet možností je opět m = 2, tj. h = ld 0,5 = 1 bit.

Příklad:
Jaký informační obsah (rozsah) má n-místné decimální číslo?
Informační obsah (rozsah) jedné decimální cifry je ld 10 = 3,32 bitu. (Výpočet: log 10 / log 2 = 1 / 0,30103 = 3,32 bitu)
Číslo skládající se z n cifer má tak následující informační obsah (rozsah) h = ld 10ⁿ = n ld 10 = n * 3,32 Pro optimální kódování n-místného decimálního čísla je zapotřebí n * 3,32 bitů.
Kontrolní otázka: Jaký informační rozsah mají následující ikóny, které zobrazují počet úhlů ? Počítají se úhly menší nebo rovné 90 stupňům.

Poznámka: Nepodobají se tyto ikóny nápadně symbolům tzv. arabských cifer? Argumentuje se tak, že počet úhlů v ikónách by mohl souviset se zobrazováním počtu úhlů staveb. Tento příklad představuje určitou neověřenou (www.orthohelp.com/number.htm) a popíranou teorii (nostalgia.wikipedia.org/wiki/Arabic_numerals/¨talk), kterou jsme v detailech upravili. Sedmička je zobrazena tak jak se učí ve slovanských školách a nikoliv v anglofilních a odstraněna byla devítka a nula. V případě devítky se přidává ještě jeden úhel u nožičky, což se ale na tomto místě špatně zobrazuje. A poněvadž se říká „dostat kulové“, tj nedostat nic, tak tu také není zobrazena nula, poněvadž dostáváte kulové. Slovo „cifra“ nebo „cipher“ je údajně arabského původu a znamená nula (http://home.att.net/~Berliner-Ultrasonics/language.html, Islamic Center of Long Island, http://muslimsonline.com/icli). Z ikónů se symboly staly tak, že se ztratila informace o počtu úhlů a cifry se zakulatily či jinak znetvořily.
(Key: number of angles, arabic numerals, meaning of numbers)
Odpověď na kontrolní otázku: log 8 / log 2 = 3 bity

Příklad:
Použijme k hodu takovou minci, která není symetrická (chybně vyrobená, ohnutá apod.). V 90 % všech vrhů padne panna, jinak lev. Pravděpodobnost panny je tedy p_panna = 0,9 a pravděpodobnost lva p_lev = 0,1. Informace, že padla panna je rovna
h_panna = ld 1 / 0,9 = ld 1,11 = 0,15 bitu

Informace, že padl lev je rovna
h_lev = ld 1 / 0,1 = ld 10 = 3,32 bitu

U každého jevu tedy pozorujeme rozdílné množství informace. Padnutí panny očekáváme s velkou pravděpodobností a její padnutí nás nepřekvapí. Naproti tomu padnutí lva je méně očekávané a je to pro nás informace s velkým rozsahem.

Příklad:
Jakou průměrnou informaci obdržíme při několika hodech vadnou mincí? Při těchto hodech se panna podílí 0,15 bity a lev 3,32 bity. Pravděpodobnost výskytu panny je ale 9krát větší než lva. To znamená, že průměrný informační obsah je
H = (0,9 x 0,15) + (0,1 x 3,32)= 0,47 bitu
Porovnáme-li hody vadnou mincí (0,47 bitu) s běžnou mincí (1 bit), zjisťujeme, že hody s vadnou mincí poskytují méně informací. Hody s takovými mincemi jsou totiž méně nejisté.

Obecně tedy platí
H = p₁ h₁ + p₂ h₂ + … + p_x h_x = ∑ p_i h_i

Dosadíme-li za h_i = ld 1/p_i obdržíme
H = ∑ p_i ld 1 / p_i = - ∑ p_i ld p_i
což je známý Shannonův vzorec rozsahu informace nebo také střední informační rozsah (obsah) alias entropie.

C. E. Shannon (1916-2001) – tvůrce informační teorie – se svou elektronickou myší Theseus při jednom z prvních experimentů umělé inteligence.

Příklad:
Zdroj znaků vysílá znaky z abecedy {A|B|C}. V polovině případů se vysílá znak A.
Zbývající znaky s jednou čtvrtinou. Pravděpodobnost pro znak A je tedy p = 0,5 a informační obsah (rozsah) h=1. Pravděpodobnost znaku B je p = 0,25. Pro C je p=0,25.
Informační obsah (rozsah) pro znak A spočítáme podle
h = - ld p = - (ln 0,5 / ln 2) = 1/ln 2 * (- ln 0,5) = 1
Analogicky spočítáme informační obsah (rozsah) h pro znak B (h=2)
a znak C (h=2). Střední informační obsah (rozsah)
H = 0,5 * 1 + 0,25 * 2 + 0,25 * 2 = 1,5 bitu.

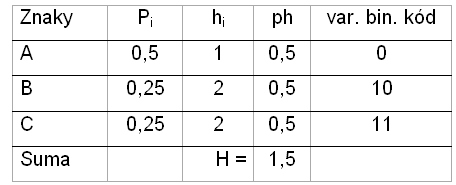
Zeptáme-li se zda byl vyslán znak A, pak zjišťujeme, že v polovině případů ano. V druhé polovině případů to byl znak B nebo C. To znamená, že jak znak B tak znak C byl vyslán s pravděpodobností 0,25. Znaky lze zakódovat variabilním binárním kódem. Co je variabilní binární kód ? Klasickým příkladem je morseovka. V anglické abecedě je nejčastější samohláska e. Proto se píše nejkratším binárním slovem – tečkou. Další v četnosti je samohláska i. Píše se proto dvěmi tečkami. Písmeno h patří do skupiny s nejnižším výskytem a píše se proto jako čtyři tečky. Morseovka je kód s variabilní délkou slov a jeho abeceda se skládá ze tří znaků {●|▬|mezera}. Známá je také zvuková varianta morseovky .

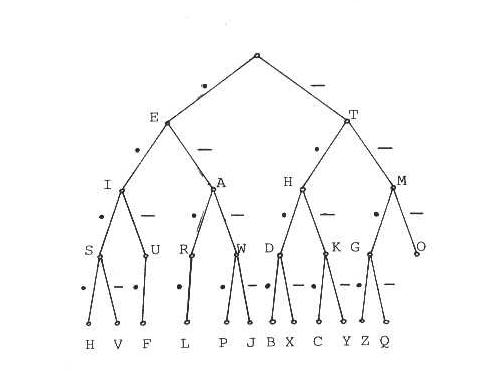
Na stromovém grafu morseovky lze odvodit jak samotný kód, tak délku kódovaných slov. Stačí sledovat hrany grafu od kořene k příslušnému písmeni. Tak například délka kódovacího slova pro písmeno P je 4 a kód je ● ▬ ▬ ● . Morseovka představuje skupinovou metodu kódování. Na základě prvního kódovaného znaku – tečka nebo čárka - se určí, do které skupiny slovo patří, pak do které podskupiny, atd. Skupinové kódování má tu přednost, že se snižuje redundance kódu.

V našem příkladě se znaky A,B a C je nejpřirozenější, že nejčastější znak budeme vysílat nejkratším binárním slovem a znaky B a C delším slovem. Bylo by neekonomické, kdybychom často se opakující znak kódovali nesmyslně nejdelšími kódy. Délku binárního slova (kódu) označujeme písmenem l (length) – viz tabulka.

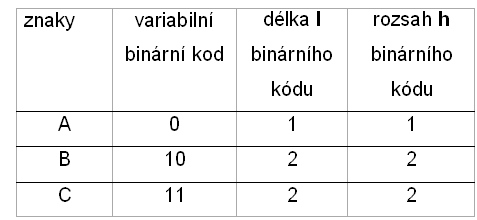
Z tabulky můžeme také odečíst, že délka každého binárního slova (kódu) je rovna informačnímu rozsahu příslušného znaku.
Proto je střední délka příslušného binárního kódu (slova) rovna střednímu informačnímu rozsahu, jak zjišťujeme porovnáním následující tabulky, kde je spočítána střední délka slova L a předchozí tabulkou, kde je spočítán střední informační obsah (rozsah) H. Toto je ideální případ. V reallitě je tomu ale jinak, což si ukážeme na příkladě. Nejprve ale jak se vypočítá střední délka slova.

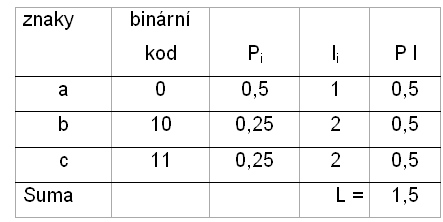
Střední délka slova L určitého kódu se spočte podle následujícího vzorce
L = ∑ p_i l_i

kde li označuje počet jednotlivých znaků binárního kódu kódujícího znak a, pi je pravděpodobnost výskytu znaku. Délka binárního kódu li závisí na volbě kódování. Informační obsah (rozsah) h_i je na kódování nezávislý.

Příklad:
Zdroj zpráv vysílá tři znaky a, b, c s danými pravděpodobnostmi P_i.
Použijme stejné kódování jako v předchozím příkladě a spočítejme střední informační rozsah H a střední délku slova L.

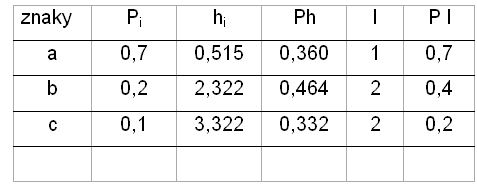
H = 1,156 bitu L = 1,3 bitu

Střední délka slova L je v tomto příkladě větší než střední informační obsah (rozsah) H, což platí ve většině případů. Rozdíl L – H označujeme redundanci
R = L – H, R je větší nebo rovno 0
Redundance udává o kolik bitů je slovo binárního kódu v průměru delší, než kolik by bylo nutné v optimálním případě. Nízká redundance ukazuje na účinné kódování, vysoká na neúčinné kódování nebo chybu. Relativní redundance je poměr redundance a střední délky kódu:

r = R/L a lze ji vyjádřit v procentech

Příklad:
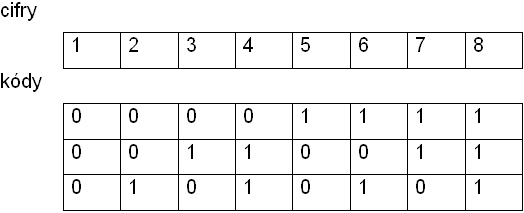
Na kódování osmičkové soustavy, tj cifer od 1 do 8, potřebujeme 3 bity.
Vidíme, že kódování není redundantní.

Příklad:
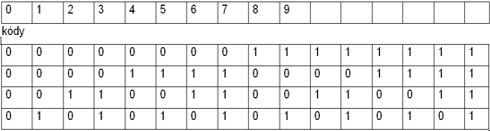
Na kódování čísla desítkové soustavy, tj. cifer od 0 do 9, potřebujeme
4 bity. Proč?
Informační rozsah (obsah) jedné číslice desítkové soustavy ld 10 = 3,32 bitů. Redundance je tedy 0.68 bitu. Kód může být pouze celočíselný, nemůžeme proto použít 3,32 bitu, nýbrž 4 bity, tj 4 znaky. Nula je kódována jako 0000, jednička jako 0001, atd. Redundance vznikla proto, že 6 kódování ze 16 je nevyužito. V praxi se proto na kódování čísel používá jiný systém.

Tak to byl málý pohled do kuchyně informatiků. Claude E. Shannon razil cestu digitální komunikaci a umělé inteligenci. Významně ovlivnil kryptografii, počet pravděpodobnosti, ekonomiku, biologii a psychologii. Vynalézal i věci, které bychom nečekali: stroj který uměl žonglovat, frisbee talíř poháněný raketovým motorkem, motorizovanou pérovací tyč na skákání a třeba zařízení, které umělo vyřešit Rubikovu krychli. Uměl si zkrátka hrát. Postavil také počítač, který uměl hrát šachy a s tehdejším mistrem světa Michalem Botvinikem prohrál až po 42 tazích.

Šachy jsme začali a šachy skončíme. Shannonovi by se to určitě líbilo. A také vzhledem k tomu, že čtenáři Osla milují pořádnou vědu. Následující partie je přímo z kavárny a vznikla pod dojmem četby bulváru jednoho kavárenského povaleče jménem Topalov (bílé kameny) a za účasti častého návštěvníka splachovacích záchodů Kramnika (černé kameny), kde prý na mistrovství v šachách 2006 elektronicky řešil příští tah proti Topalovi. Ti dva se ani trochu nemají rádi a už vůbec ne při šachách. Byla Topalova oběť koně kavárenský trik ?

1.d4 d5, 2.c4 c6, 3.Jf3 Jf6, 4.Jc3 e6, 5.Sg5 h6, 6.Sh4 dxc4, 7.e4 g5, 8.Sg3 b5, 9.Se2 Sb7, 10.0-0 Jbd7, 11.Je5 Sg7, 12.Jxf7!? (Obvykle se tady hrávalo 12.Jxd7 Jxd7 13.Sd6) 12...Kxf7, 13.e5 Jd5, 14.Je4 Ke7, 15.Jd6 Db6, 16.Sg4 Vaf8, 17.Dc2 Dxd4? (Podle Topalova je 17...Vhg8 lepší), 18.Dg6 Dxg4, 19.Dxg7+ Kd8, 20.Jxb7+ Kc8, 21.a4 b4, 22.Vac1 c3, 23.bxc3 b3 (Také po 23...Jxc3 24.De7! Je2+ 25.Kh1 Jxc1 26.Vxc1 má bílý rozhodující útok.), 24.c4 Vfg8, 25.Jd6+ Kc7, 26.Df7 Vf8, 27.cxd5 (Jednodušší vítězství by bylo 27.h3) Vxf7, 28.Vxc6+ Kb8, 29.Jxf7 Ve8, 30.Jd6 Vh8, 31.Vc4 De2, 32.dxe6 Jb6, 33.Vb4 Ka8, 34.e7 Jd5, 35.Vxb3 Jxe7, 36.Vfb1 Jd5, 37.h3 h5, 38.Jf7 Vc8, 39.e6 a6, 40.Jxg5 h4, 41.Sd6 Vg8, 42.V3b2 Dd3, 43.e7 Jf6, 44.Se5 Jd7, 45.Je6. - 1-0.

Partie byla sehrána 23. ledna 2008 v holandském Seebad Wijk aan Zee. Otevření partie: anti moskevský gambit.

18. ledna 2008 zemřel na Islandu bývalý mistr světa v šachu Bobby Fischer. Bobby zemřel v zemi svého největšího životního úspěchu – stal se tam mistrem světa. Na sklonku života tam dostal asyl před americkými úřady, které jej pronásledovaly za to, že si 1992 zahrál šachy v Jugoslavii. Jirka Křovák tehdy svým občanům návštěvu Jugoslavie zakázal. V jedné studii je doloženo, že mezi vrcholnými managery a vrcholnými politiky je více psychopatů než v jedné velké věznici.

================================== Pokračování článku zde