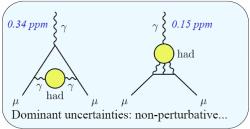
Jedním z nejčastějších témat diskuzí, které probíhaly v kuloárech konference ICHEP 2024, tedy alespoň těch, kterých jsem se účastnil, byly nové teoretické výpočty magnetického dipólového momentu mionu. I když připouštím, že to je můj subjektivní pohled. Nové výpočty probíhaly dominantně v oblasti příspěvku silné interakce a vedly k tomu, že se nově určená teoretická hodnota v mezích nejistot experimentálního a teoretického výsledku neliší od té experimentální. Tím jsme přišli o jeden z nejlépe vypadajících signálů nové exotické fyziky za Standardním modelem hmoty a interakcí.
Mion, stejně jako elektron, mají magnetický dipólový moment a jsou tak malými magnetkami. Jde o veličinu, kterou lze měřit s extrémně vysokou přesností, a i teoreticky vypočet její hodnoty s využitím Standardního modelu hmoty a interakcí lze realizovat se srovnatelně vysokou přesností. Odchylka mezi experimentální a teoretickou hodnotou je pak projevem signálů nové fyziky, která je za tímto Standardním modelem.
Před třemi lety byly publikovány nové výsledky měření hodnoty magnetického dipólového momentu experimentem Muon g-2, který pracuje v laboratoři Fermilab ve Spojených státech. Ten plně potvrdil předchozí měření experimentu E821 v laboratoři v americkém Brookhavenu. Experiment v laboratoři Fermilab využívá velice intenzivní zdroj mionů, který poskytují tamní urychlovače. Všechny části experimentu byly nové, pouze magnet, který je náročný a drahý, se převezl z Brookhavenu do Fermilabu. Nová nezávislá měření dospěla ke stejné hodnotě magnetického dipólového momentu mionu. Způsob měření a další detaily o experimentálním i teoretickém určování magnetického dipólového magnetu jsou v dřívějším článku o výsledcích experimentu v laboratoři Fermilab.
Teorie magnetických dipólových momentů částic ve Standardním modelu
Připomeňme si teorii, která se využívá k určení hodnoty magnetického momentu, s využitím popisu uvedeném už ve zmíněném dřívějším článku. Standardní model hmoty a interakcí obsahuje částice hmoty, kterými jsou šestice kvarků (u, d, s, c, b, t) a šestice leptonů (elektron, elektronové neutrino, mion, mionové neutrino, tauon, tauonové neutrino), a také jejich antičástice. Dále obsahuje i interakce, které umožňují vytváření vázaných systémů a přeměnu částic mezi sebou. Ty se v této teorii popisují pomocí kvantových teorií polí prostřednictvím výměny částic ve virtuální podobě. Existují tři interakce. Silná, která působí pouze na kvarky je zprostředkovaná osmicí gluonů ve virtuální podobě. Elektromagnetická, která je zprostředkovaná fotony ve virtuální podobě. Slabá interakce, to je jediná interakce působící na neutrina, je zprostředkována bosony W+, W- a Z ve virtuální podobě. Ve Standardním modelu je ještě jedna částice, kterou je Higgsův boson. Ten je spojen s mechanismem, který generuje rozdíl mezi hmotnostmi fotonu a bosonů W a Z. Podrobnější popis částic Standardního modelu i těch hypotetických mimo něj jsou v dřívějším článku.
Kvantově polní popis interakcí je daleko komplikovanější, než je výměna jednotlivých zmíněných virtuálních částic. Může se při tom vyměňovat více virtuálních částic. A dokonce přispívají k interakcím komplexní výměny, kde figurují i virtuální podoby částic hmoty. Při interakci se tak vytvářejí a zanikají virtuální páry leptonu a antileptonu nebo kvarku a antikvarku.

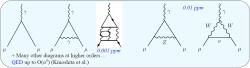
Příspěvky jsou tím menší, čím je větší a komplexnější systém vznikajících a zanikajících virtuálních částic. Jednotlivé z nich můžeme popsat pomocí tzv. Feynmanových diagramů, kde jsou virtuální částice zobrazeny různým typem linie nebo vlnovky mezi pevnými vrcholy grafů. Reálné částice mají jeden konec volný, je buď na začátku nebo konci grafu. U virtuálních je to složitější, ale většinou končí oba jejich konce ve vrcholech. Velikost příspěvku daného grafu je dána počtem jeho vrcholů. Čím více vrcholů je, tím je příspěvek grafu menší.
Virtuální částice, jejichž „doba existence“ je omezena Heisenbergovým principem neurčitosti, mohou mít klidovou energii (hmotnost) vyšší i řádově, než je energie v systému dostupná. Na této úrovni tak nemusí být splněn zákon zachování energie.
Lze se však na to dívat i z jiného pohledu. Definuje se, že virtuální částice není na hmotové slupce a nesplňuje rovnici E2=E02+p2c2, kterou musí splňovat každá reálná částice. Zde je E celková energie, p hybnost a E0 klidová energie částice daná její klidovou hmotností E0=m0c2. V tom případě není nutné opustit splnění zákonu zachování energie a hybnosti.
Čím je klidová energie dané virtuální částice větší, tím je příspěvek daného diagramu k interakci menší. Vakuum, ve kterém se pohybují reálné částice tak není prázdné, ale je vyplněno neustále vznikajícími a zanikajícími virtuálními částicemi (možná lépe řečeno stavy). Podrobnější rozbor komplexního popisu vakua pomocí kvantové teorie pole je ve starším článku.
Některé částice ve Standardním modelu mají magnetický dipólový moment, jsou magnetkami, které vytvářejí magnetické pole. Pokud jsou dané částice bodové, měl by být jejich dipólový magnetický moment dominantně dán jejím spinem (vnitřním momentem hybnosti), u něj je závislost lineární. Stejně tak je lineárně závislý na elektrickém náboji částice. Naopak na hmotnosti je závislý nepřímo úměrně. Elektron, mion mají stejný spin i elektrický náboj. Naopak jejich hmotnosti se dramaticky liší. Takže magnetický dipólový moment elektronu je větší, protože jeho hmotnost je menší. Hmotnosti mionu je téměř dvěstěkrát větší, jeho magnetický moment je tak skoro dvěstěkrát menší.
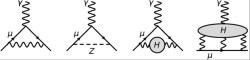
I u bodových částic se objevují odchylky od jednoduché předpovědi. V tomto případě jsou však „anomálie“ velmi malými korekcemi danými interakcemi s kvantovými polí popisujícími vakuum v okolí částic (polarizace vakua). Ty jsou dány popsanými vlastnostmi vakua (polí) v okolí částice a jsou popsány zmiňovanými Feynmanovými diagramy se stále větším počtem vrcholů a počtem virtuálních částic (stavů), které v okolním vakuu stále vznikají a zanikají. Pokud chceme pomocí kvantově polních teorií Standardního modelu spočítat velikost této opravy, musíme zahrnout všechny možné Feynmanovy diagramy se stále větší úrovní komplexnosti a stále větším počtem vrcholů. Příspěvky můžeme rozdělit na tří části. První příspěvky jsou dány kvantovou elektrodynamikou a vystupují v nich virtuální leptony a fotony, druhé jsou způsobeny elektroslabou interakcí a vystupují tam W a Z bosony i higgsy. Třetí příspěvky jsou spojeny s kvantovou chromodynamikou (silnou interakcí) a jde o diagramy, kde jsou virtuální kvarky a gluony (hovoříme hadronové polarizaci vakua). Příspěvky prvního a druhého typu se dají počítat ze základních principů teorie a velice přesně. Přesnost je zde omezena jen matematickou náročností a velikostí potřebného počítačového výkonu. U třetího typu je situace složitější, tam potřenou teorii neznáme na potřebné úrovni a jejich výpočet je komplikovanější a jeho přesnost je závislá na přesnosti experimentálních dat silně interagujících částic.
Problém pro srovnání experimentu a teorie tak není jen dosažení co největší přesnosti měření, ale také zajištění co nejpřesnější určení teoretické hodnoty. Kvantová elektrodynamika, jejíž vliv dominuje zvláště u lehkého elektronu, umožňuje určit jeho magnetický dipólový moment s extrémní přesností. Jeho hodnotu můžeme rozdělit na součin dvou částí. První je součin tzv. gyromagnetického poměru g a spinu částice, druhým pak magneton dané částice, který je dán podílem jejího náboje a hmotnosti a některých fyzikálních konstant (Planckovy konstanty a rychlosti světla). Druhý člen v podstatě představuje přirozenou jednotku, ve které daný magnetický moment vyjadřujeme.
Pro bodovou částici je gyromagnetický poměr 2. Pokud má spin 1/2, jako je to u elektronu a mionu, je hodnota před jednotkou 1. Jak bylo zmíněno, lze u elektronu opravy na korekce stále vyšších řádů vyplývající z kvantové teorie pole pro gyromagnetický poměr určit s extrémní přesností. Teoreticky stanovené číslo před jednotkou magnetického momentu, která se v případě elektronu označuje jako Bohrův magneton, je tak v současné době:
gˑI = 1,001 159 652 181 64(76)
V závorce je nejistota tohoto určení. Nejpřesněji změřená hodnota je v současné době:
gˑI = 1,001 159 652 180 73(28)
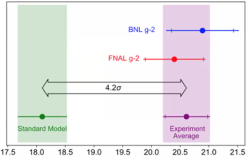
Je vidět, že rozdíl mezi experimentem a teorií se projevuje až na třinácté až čtrnácté platné cifře a je v mezích uvedených experimentálních nejistot.
Nový výpočet hodnoty magnetického dipólového momentu mionu
Mion je skoro dvěstěkrát těžší, než je elektron. Jeho anomální část magnetického momentu je silněji ovlivněna příspěvky, které nepatří do kvantové elektrodynamiky, tedy i těmi spojenými se silnou interakcí popisovanou kvantovou chromodynamikou. A je i větší šance, že se zde projeví i vliv nové exotické fyziky za Standardním modelem. Tato nová fyzika může také obsahovat nové částice. Ty sice mohou být mnohem těžší, než jsou ty ze Standardního modelu. Nelze je tak produkovat ani na těch největších urychlovačích, jako je třeba LHC. Ovšem mohou být ve virtuální podobě přítomny ve Feynmanových diagramech, které popisují anomální část magnetického momentu mionů. Projeví se tak ve velikosti odchylky teoretické hodnoty určené jen ze Standardního modelu od té experimentální. Experimentální hodnota určená jako střední vážená hodnota zmíněných měření v laboratořích Brookhaven a Fermilab je:
gˑI = 1,001 165 920 61(41)
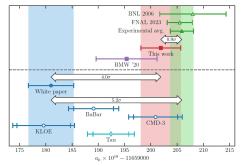
Dřívější teoretická hodnota pro magnetický dipólový moment se lišila od té experimentální s uváděnými nejistotami o více než čtyři standardní odchylky (viz obrázek).
Byly tři možnosti vysvětlení daného rozdílu. První byla neodhalená chyba v experimentu, která nebyla započtena do systematické nejistoty experimentálního výsledku. Druhou pak mohla být neodhalená chyba teoretického výpočtu s využitím Standardního modelu hmoty a interakcí, která se nezapočítala do systematických nejistot teoretické hodnoty. No a poslední by byla pro nás nejzajímavější, mohlo by se jednat o projevy nové exotické fyziky za Standardním modelem.

Nyní se ukazuje, že správně je s vysokou pravděpodobností druhá možnost. Jak bylo zmíněno, je největší nejistota v příspěvku z hadronové polarizace vakua, nejistoty z příspěvku polarizace vakua elektromagnetického a elektroslabého jsou menší a to i v případě vyšších řádů. Dominantní část nejistoty tak pochází z omezení naši schopnosti popisovat silnou interakci. Kvůli velmi silné vazebné konstantě, je možnost využití poruchových metod omezená a přesné výpočty jsou velmi náročné. Přesnost pochopitelně závisí i na přesnosti určení volných parametrů Standardního modelu hmoty a interakcí souvisejících se silnou interakcí, které se určují filtrem širokého souboru experimentálních dat.
Při výpočtech příspěvků silné interakce se široce využívají metody výpočtů QCD (kvantové chromodynamiky) na mříži. A právě nedávno publikovaná práce prezentovala dramatické zlepšení výpočtů hadronové polarizace vakua dosažené zjemněním mřížových výpočtů, které umožnilo zpřesnění extrapolace kontinua. Autoři zahrnuly i malý příspěvek na větší vzdálenost získaný z výsledků experimentu v oblasti nízkých energií. Využili také detailní shrnutí výpočtů ostatních příspěvků ze Standardního modelu hmoty a interakcí. Podařilo se jim docílit podstatného zpřesnění a snížení systematických nejistot. Jimi získaná teoretická výsledná hodnota magnetického dipólového momentu je v perfektní shodě s tou experimentální. Rozdíl je menší než jedna standardní odchylka, tedy existuje shoda v rámci nejistot výpočtu a experimentu.
Závěr
Nové zpřesněné výpočty postavené na Standardním modelu hmoty a interakcí umožnily spočítat hodnotu magnetického dipólového momentu mionu. Nová teoretická hodnota je ve velmi dobré shodě s experimentální hodnotou potvrzenou a zpřesněnou před třemi lety ve Fermilabu. Může být zklamáním, že se „ztratil“ signál nové exotické fyziky. Extrémně přesné potvrzení Standardního modelu není tak atraktivní. Ale přesto, ověření jeho správnosti a v širším kontextu ověření renormalizované kvantové teorie pole na úrovni 0,35 ppm (zlomku miliontiny) je opravdu fantastický pokrok. Přitom se u experimentu Muon g–2 stále nabírají data a mělo by postupně dojít k dalšímu zpřesnění experimentální hodnoty magnetického dipólového momentu mionu. Stejně tak se postupně pracuje i na zpřesnění hodnot parametrů Standardního modelu a metod výpočtu hlavně příspěvku hadronové polarizace vakua. Lze tak čekat ještě další zpřesnění ověřování Standardního modelu pomocí této veličiny. A třeba se na ještě vyšší úrovni přesnosti konečně objeví i ta nová exotická fyzika. Zatím se však stále potvrzuje, že současná teorie struktury hmoty, kterou je právě Standardní model hmoty a interakcí, je opravdu fantasticky přesný nástroj.
Přednáška o kvantovém vakuu pro Café Nobel (i zde jsem zmiňoval, že rozdíl teoretické a experimentální hodnoty magnetického dipólového momentu může být známkou nové exotické fyziky)
Budoucí kruhový urychlovač v CERN
Autor: Marek Taševský (14.05.2014)
Jak se vyznat v přehršli různých částic
Autor: Vladimír Wagner (31.08.2014)
Magnetka mionu míří k nové fyzice
Autor: Vladimír Wagner (08.04.2021)
Diskuze: