Nejmladší pulsar se skrývá v Krabí mlhovině (zdroj ESA).

Hmota v jádře má specifické vlastnosti, které jsou dány tím, že nukleony jsou fermiony. Navíc teplota fermionové hmoty v jádře je extrémně nízká a jedná se o její formu, kterou označujeme jako degenerovaný fermionový plyn. Taková hmota se vyskytuje i v nitru neutronových hvězd. Zatímco nukleony v jádře drží silná jaderná síla, v neutronových hvězdách je to síla gravitační. Tlaku, který vyvolává, musí odolávat právě tlak fermionového plynu. Pokud hmotnost neutronové hvězdy roste, roste nejen gravitační tlak, ale i kinetická energie fermionů ve zmíněném plynu. Pokud naroste tak, že bude mnohem větší, než je klidová energie těchto fermionů a jejich rychlost bude téměř rychlostí světla, dostaneme tzv. ultrarelativistický degenerovaný fermionový plyn.

A jak ukázal právě Robert Oppenheimer, ten už nedokáže odolávat gravitačnímu tlaku a hvězda se nezadržitelně zhroutí do černé díry. Přesná limitní hmotnost, při které ke kolapsu dojde, a tedy nejvyšší možná hmotnost neutronové hvězdy, závisí i na některých dalších vlastnostech samotné neutronové hvězdy a také na jejím složení. Pokud neutronová hvězda rychle rotuje, odstředivá síla jí pomáhá odolávat kolapsu. Stejně tak se mění odolnost proti kolapsu se změnou složení fermionového plynu. Neutronová hvězda se nemusí skládat pouze z neutronů, které jsou v jejím názvu, ale může obsahovat i hyperony.

Pokud hmotnost neutronové hvězdy překročí určitou hodnotu, nezadržitelně se zhroutí do černé díry. Pozorovat ji můžeme, pokud je ve dvojhvězdě s hvězdou, ze které na ní přetéká hmota, vytváří se akreční disk a výtrysky částic (zdroj NASA).

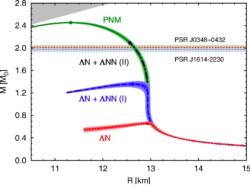
V případě přítomnosti hyperonů by se podle našich současných znalostí měla stavová rovnice jaderné hmoty s jejich přítomností „změkčovat“ a odolnost neutronové hvězdy proti kolapsu snižovat. A naše současné představy naznačují, že by v neutronových hvězdách hyperonová hmota být měla. Neměla by tak existovat neutronová hvězda s hmotností dvou hmotností Slunce a vyšší. Ovšem naše astronomické přístroje pozorují i neutronové hvězdy překračující tuto hmotnostní limitu. Je tak otázkou, jestli je chyba v našich měřeních hmotností neutronových hvězd, nebo se naopak mýlíme v našich teoriích popisujících vlastnosti hyperonů, hyperonové hmoty a neutronových hvězd. Tento rozpor se označuje jako hyperonová hádanka a patří k velké výzvě při studiu vlastností velmi husté jaderné hmoty a kompaktních konečných stádií hvězd. Podívejme se tak, jaká je současná situace v cestě za vyřešením této hyperonové hádanky.

Vlastnosti fermionů a degenerovaného fermionového plynu v jádře

Fermiony jsou „nesnášenlivé“ částice, v jednom kvantovém stavu, charakterizovaném polohou a hybností, s odpovídající energií může být pouze jediná stejná částice. Pohybujeme se v mikrosvětě, kde vládnou zákony kvantové fyziky. A statistika, které se jednotlivé částice podřizují, tedy jestli může být jen jedna nebo více stejných v jednom kvantovém stavu, je dána tím, jaká je hodnota jejich spinu. Spin je veličina, která má fyzikální rozměr momentu hybnosti. Stejně jako celá řada dalších veličin v kvantovém světě, existují jen diskrétní hodnoty spinu. V jednotkách redukované Planckovy konstanty jde o celočíselné nebo poločíselné hodnoty. Poločíselné hodnoty mají právě fermiony a pro ně platí Fermi-Diracova statistika a v kvantovém stavu může být pouze jedna stejná částice s danou projekcí spinu. Celočíselné hodnoty spinu mají bosony, které se podřizují Bose-Einsteinově statistice. V tomto případě může být v jednom kvantovém stavu hodně stejných částic.

V jádře jsou dva druhy fermionů, protony a neutrony, a tím i dvě potenciálové jámy. V každém energetickém stavu jsou dvě možné projekce spinu nukleonu se spinem ½.

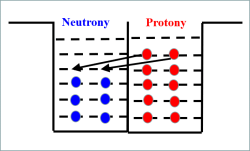
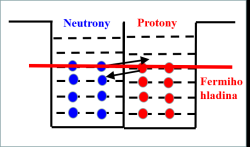
V jádře máme nukleony, které mají spin ½ a jsou tak fermiony. Jsou dvojího typu, kladně nabité protony a neutrální neutrony. Z pohledu silné jaderné interakce jsou protony a neutrony stejnými částicemi, a na obě tak tato interakce působí stejně. Silná jaderná síla je přitažlivá a na rozdíl od elektromagnetické interakce působí jen na krátkou vzdálenost, něco málo přes jeden femtometr, tedy zhruba 10^-15 m. Každý nukleon tak interaguje pouze s velmi omezeným počtem dalších nukleonů. Nukleony tak společně vytváří potenciálovou jámu, ve které vznikají diskrétní stavy s rostoucí energií. V každém z těchto stavu může být nejvýše jeden stejný fermion. V základním stavu jsou pak u jádra zaplněny všechny stavy od té nejnižší až po určitou hodnotu energie. Všechny stavy nad touto hodnotou energie, která se označuje jako Fermiho energie, jsou prázdné. Jedná se tak o degenerovaný fermionový plyn s nulovou teplotou. Je to stav s nejnižší možnou energií. Jádro v excitovaném stavu má obsazeny některé stavy nad Fermiho energií a má prázdná místa u některých stavů pod ní.

Pokud bychom vypnuli elektromagnetickou interakci, bude hloubka potenciálové jámy u protonů a neutronů stejná.

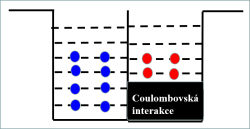
Připomeňme, že v jádře máme dva druhy fermionů, protony a neutrony, tedy dvě potenciálové jámy. Zároveň může v jádře docházet k přeměně protonu na neutron nebo neutronu na proton. Nejnižší energie systému se dosáhne, když je Fermiho energie u protonů a neutronů vyrovnaná. V případě, že by byla vypnuta elektromagnetická interakce a hloubku potenciálové jámy by neovlivňovalo vzájemné odpuzování kladně nabitých protonů, byla by stejná. Příroda má ráda systémy s co nejnižší energií. Pro stabilní jádro by tak počet protonů a neutronů byl stejný.

V jádře však působí odpudivá coulombovská síla způsobená elektromagnetickou interakcí mezi kladně nabitými protony. Ta snižuje hloubku potenciálové jámy u protonů. I v tomto případě jsou pro stabilní jádra Fermiho hladiny u protonů a neutronů vyrovnány. U těžších jader, kde začíná být vliv odpudivé coulombovské síly patrný, je tak u stabilních jader menší počet protonů než neutronů.

Pokud by byl počet neutronů vyšší, jádro by bylo nestabilní a pomocí radioaktivní beta přeměny by se v něm neutron přeměnil na proton. Stejně tak by to probíhalo v případě, kdyby bylo více protonů než neutronů. V tomto případě by se proton přeměnil na neutron. Neutron má hmotnost větší než proton. Ve vakuu je tak nestabilní a přeměnou beta se za vzniku elektronu a antineutrina mění na proton. V stabilním jádře je však stabilní. Všechny stavy s nižší energií (pod Fermiho hladinou) jsou u protonů obsazené.

Protony, neutrony a hyperony jsou složeny z kvarků. To, jaké kvarky je tvoří, určuje i jejich hmotnost.

Nově vzniklý proton se tam usadit nemůže. Pro přechod do těch s vyšší energií by potřeboval dodatečnou energií, a ta získaná při přeměně neutronu na proton, elektron a antineutrino k tomu nestačí.

Přidání hyperonů – dostaneme hyperjádra

Protony a neutrony patří mezi částice interagující silnou interkcí, které se společně označují jako hadrony. Hadrony jsou složené z kvarků. Existují jich dva typy. Baryony, kterými jsou právě i protony a neutrony, se skládají ze tří kvarků a jejich antičástice ze tří antikvarků. Kvarky jsou fermiony a fermiony jsou pak i baryony. Mezony se skládají z jednoho kvarku a jednoho antikvarku a jsou bosony.

U hyperjader máme ještě třetí potenciálovou jámu, ve které jsou hyperony. Neutrony se nemohou v jádře přeměnit na hyperony, protože by potřebovaly energii, která by je poslala pod dno potenciálové jámy hyperonů. Hyperony se v jádře mohou rozpadat, protože je energie uvolněná při jejich přeměně pošle do volných stavů v potenciálové jámě neutronů nebo nad ní.

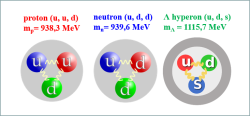
Protony a neutrony se skládají z dvojice nejlehčích kvarků u a s. Existují však i baryony, které obsahují třetí kvark s, který je mnohem těžší, než jsou kvarky u a d. Ty se označují jako hyperony. Podivné částice, jak se říká těm, které obsahují kvarky s, byly objeveny na přelomu čtyřicátých a padesátých let minulého století. Vznikaly s vysokou pravděpodobností silnou interakcí většinou ve dvojicích. Ovšem rozpadaly se na nepodivné částice o mnoho řádů pomaleji, než by odpovídalo silné interakci a rozdílu hmotností rozpadající se částice a produktů rozpadu. Musely se tak rozpadat slabou interakcí. Pro orientaci ve světě částic jsem napsal podrobný přehled.

Vysoká pravděpodobnost vzniku a relativně dlouhá doba života byla velkým překvapením, proto se začaly tyto částice označovat za podivné. Bylo jasné, že existuje fyzikální veličina, kterou podivné částice mají a pro silnou interakci platí zachování této veličiny. Změnit její hodnotu může pouze slabá interakce. Dnes víme, že tuto veličinu, označovanou jako podivnost, nese právě kvark s. Pouze slabá interakce umožňuje přeměnit tento kvark na lehký kvark.

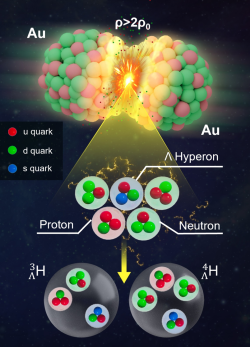
Podivný hyperon lambda je neutrální a podobný neutronu. Je však o téměř 20 % těžší. Ve vakuu se rozpadá s dobou života 0,26 ns (tedy v řádu 10^-9 s) nejčastěji na proton a záporný mezon pí nebo na neutron a neutrální mezon pí. Jestliže lambda hyperon přidáme do jádra, dostaneme třetí potenciálovou jámu a v ní třetí typ fermionů. Vznikne tak hyperjádro.

Přesná hloubka hyperonové potenciálové jámy závisí na silné jaderné interakci mezi hyperony a hyperony a nukleony. V každém případě však hyperony sedí energeticky níže, než je Fermiho hladina protonů a neutronů. Ovšem pro přeměnu protonu nebo neutronu na lambda hyperon by byla potřeba velká energie a tu si jádro nemá kde vzít. Naopak, při přeměně lambda hyperonu na neutron a mezon se energie uvolní. Vzniklý proton a neutron se tak dostává vysoko nad Fermiho hladinu protonů a neutronů. Dokonce může z potenciálové jámy uniknout. Doba života hyperjader je tak srovnatelná s dobou života hyperonů, tedy v řádů zlomku nanosekundy.

Mapa pozorovaných hyperjader (zdroj P. Achenbach).

Připomeňme, že charakteristické časy procesů realizovaných silnou interakcí jsou kratší než 10^-20 s. Hyperon a hyperjádro tak existují o více než deset řádů déle. Deexcitace vybuzených stavů jader emisí fotonu gama pak probíhá bez zpomalení s dobou života 10^-15 s, což je o pět řádů kratší čas, než je doba života hyperjader. Je tak možné produkovat excitované stavy hyperjader a s využitím spektrometrie gama studovat jejich deexcitaci. Taková studia nám přináší důležitou informaci o vlastnostech interakce mezi hyperonem a nukleony.

Přehled hyperjader s jedním hyperonem (zdroj P. Achenbach).

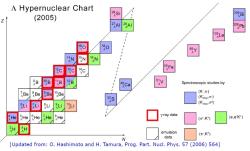
Na popis mnohonukleonových systémů se zaměřením na ty, které obsahují hyperony, se zaměřují kolegové z teoretického oddělení našeho ústavu. Problémem je, že v daném případě se neprojevují pouze dvoučásticové síly, které lze studovat v nukleon-nukleonovém rozptylu, ale i mnohočásticová komponenta silných interakcí. A právě studium energetických stavů v hyperjádrech přispívá k poznání interakcí mezi hyperony a nukleony. Do současné doby bylo pozorováno a zkoumáno okolo čtyřiceti hyperjader, a některé z nich mají i dva hyperony lambda. Pro příklad jmenujme _ΛH³, _ΛHe⁵, _ΛLi⁹, _ΛB¹², _ΛO¹⁶, _ΛFe⁵⁶, _ΛBi²⁰⁹, _ΛΛHe⁶, a _ΛΛBe⁸. Pozorují se dokonce i antihyperjádra (konkrétně antihypertriton). Podrobněji o jeho objevu si lze přečíst v dávnějším článku. Experimentální data ze zkoumání hyperjader, společně s daty z rozptylu nukleonů se konfrontují s modely popisujícími interakci nukleonů a hyperonů v jádrech a hyperjádrech. Na základě tohoto srovnání lze teoretické modely vylepšovat a zpřesňovat.

Fermionový degenerovaný plyn v poli silné jaderné interakce

Na jádro se můžeme podívat jako na objekt složený z degenerovaného fermionového plynu a vytvořit odpovídající model jádra. Dva stejné fermiony nemohou být společně v jednom stavu. Zároveň však pro mikroskopické částice, tedy i nukleony, platí Heisenbergův princip neurčitosti. Ten spojuje neurčitost v poloze částice s neurčitostí v její hybnosti. Součin neurčitosti souřadnice v ose x a složky hybnosti v ose x nemůže být menší než redukovaná Planckova konstanta. Totéž platí i pro ostatní dvě souřadnicové osy. Pokud vezmeme tři prostorové a tři hybnostní souřadnice, dostaneme šestirozměrný fázový prostor. V tomto fázovém prostoru vytváří Heisenbergův princip neurčitosti buňky vytvářené nejistotami v určení polohy a hybnosti, ve kterých nelze hodnotu těchto veličin odlišit a může tam být pouze jeden stejný fermion. Známe objem konkrétního jádra a také počet jeho protonů a neutronů. Hybnost každého z typů nukleonů je od nuly po Fermiho hybnost, která je svázána s hodnotou Fermiho energie. Z počtu protonů (neutronů) můžeme určit počet buněk ve fázovém prostoru a tím i potřebný objem ve fázovém prostoru, a tak i Fermiho hybnost a Fermiho energii protonů (neutronů). Zároveň tak model jádra jako degenerovaného fermionového plynu umožňuje určit celkovou i střední kinetickou energii nukleonů v jádře i velikost jejich tzv. Fermiho pohybu. Pokud k hodnotě Fermiho energie připočteme separační energii pro neutrony, získáme také hloubku dané potenciálové jámy. Tuto znalost lze využít při formování potenciálu silné jaderné síly, který se dosadí do Schrӧdingerovy rovnice a umožní určit stavy ve slupkovém modelu jádra. Získáme tak konkrétní hodnoty energií těchto stavů. Jaké jsou různé typy jaderných modelů a jak se s nimi pracuje je popsáno v dřívějším článku.

Nejbližší bílý trpaslík je u hvězdy Sírius. Ztrácí se tak v záři této hvězdy a jeho zobrazení je tak výzvou. Fotografie byla pořízena Hubbleovým teleskopem (zdroj NASA).

Fermionový degenerovaný plyn v gravitačním poli

V jádře jsou fermiony, kterými jsou nukleony a hyperony, drženy pohromadě silnou jadernou interakcí. V konečných kompaktních stádiích hvězd jsou fermiony drženy pohromadě v gravitačním poli. Vysoká intenzita gravitačního pole vede i k vysoké Fermiho energii, což velmi silně ovlivňuje vlastnosti takového objektu.

Bílý trpaslík – degenerovaný elektronový plyn

Prvním kompaktním konečným stádiem života hvězdy, kde se vyskytuje degenerovaný fermionový plyn, je bílý trpaslík. V tomto případě jsou těmi fermiony elektrony, které mají také spin ½. Hvězda, která spotřebovala veškeré dostupné palivo, odolává gravitačnímu kolapsu právě tlakem vytvářeným degenerovaným fermionovým plynem.

U bílého trpaslíka je hmotnost při znalosti chemického složení přímo svázána s počtem elektronů. Pro danou hmotnost lze spočítat gravitační potenciální energii v závislosti na poloměru. Zároveň pak lze v závislosti na poloměru vyjádřit pro danou hmotnost (počet elektronů) Fermiho energii elektronů a jejich celkovou kinetickou energii.

Neutronová hvězda má komplikovanou strukturu a o hmotě v jejich centrálních oblastech máme zatím omezené znalosti (zdroj Illustration of Cassiopeia A: NASA/CXC/M.Weiss).

Celková energie bílého trpaslíka je pak dána součtem jeho potenciální a kinetické energie. Příroda má ráda nejnižší energetický stav. Najdeme tak minimum celkové energie a poloměr, který pro ně odpovídá dané hmotnosti. Získáme tak poloměr bílého trpaslíka s danou hmotností. Pro jednu sluneční hmotnost nám vychází poloměr zhruba 7000 km. Bílý trpaslík o hmotnosti Slunce tak má zhruba rozměr Země.

Rovnice popisující degenerovaný fermionový plyn se začne dramaticky lišit, pokud se kinetická energie začne blížit klidové energii elektronu a elektrony v bílém trpaslíkovi přestanou být nerelativistické. Pokud dokonce kinetická energie elektronů začne dominovat nad klidovou a elektrony se stanou ultrarelativistickými, jejich rychlosti budou téměř rychlostmi světla, přestane mít po překročení určité hmotnosti degenerovaný fermionový plyn schopnost odolávat gravitačnímu kolapsu a bílý trpaslík se zhroutí do neutronové hvězdy.

Tato hraniční hmotnost, která je zhruba okolo 1,4 M_S (hmotnosti Slunce), se nazývá Chandrasekharova limita. Označuje se podle indického fyzika Subrahmanyan Chandrasekhar, který existenci této limitní hmotnosti ukázal v rámci své doktorandské práce v roce 1935.

Neutronová hvězda – degenerovaný neutronový plyn.

Při kolapsu příliš hmotné hvězdy dojde k přeměně dvojic protonu a elektronu na neutrony. Při gravitačním stlačení tak dostaneme degenerovaný fermionový plyn složený právě z neutronů. Podobně jako elektronový degenerovaný plyn odolává gravitačním tlakům i ten neutronový, ale ještě větším. Podobným způsobem jako u bílého trpaslíka lze určit i u neutronové hvězdy dané hmotnosti Fermiho energii i její poloměr. Rozdíl je v tom, že u neutronové hvězdy je zhruba dvojnásobný počet fermionů (závisí to na chemickém složení bílého trpaslíka) a hmotnost neutronu je téměř 2000krát větší než ta elektronu.

Poloměr neutronové hvězdy o hmotnosti Slunce vychází okolo 12 km, což je zhruba poloměr planetky Eros. Střední hustota pak převyšuje hustotu hmoty v atomovém jádře. V tomto případě už je poloměr tak malý, že na povrchu neutronové hvězdy je intenzita gravitačního pole tak vysoká, že se při jejím popisu neobejdeme bez Obecné teorie relativity.

John Wheeler (zdroj University of North Carolina).

A musíme ji použít i při určení chování degenerovaného neutronového plynu v ultrarelativistické limitě. I v tomto případě zjistíme, že od jisté limitní hmotnosti už takový fermionový plyn nedokáže odolávat gravitačnímu kolapsu a neutronová hvězda se nezadržitelně zhroutí. A tentokrát nemáme žádnou známou formu hmoty, která by gravitační kolaps dokázala zastavit. Hvězda se tak zhroutí pod Schwarzildův poloměr do černé díry. Tato hraniční hmotnost, která je někde mezi 2 – 3 hmotnostmi Slunce, se označuje jako TOV limita (Tolman-Oppenheimer-Volkoffova limita). Název je spojen se jmény tři fyziků, kteří se na jejím objevu podíleli. Prvním je americký astrofyzik Richard Chace Tolman, který publikoval odpovídající řešení Obecné teorie relativity. Dalšími pak Robert Oppenheimer a jeho student George Volkoff, kteří využili práci Tolmana a popsali nezadržitelný kolaps neutronové hvězdy při překročení jisté hraniční hmotnosti. Článek o kolapsu neutronové hvězdy publikovali v časopise Physical Review v únoru 1939.

Intermezzo: Robert Oppenheimer a John Archibald Wheeler

Podrobněji o osudu Roberta Oppenheimera a srovnání reality s filmem je v nedávném článku na Oslovi. Tady se podíváme pouze na tu jeho část, která je spojena se zkoumáním kompaktních konečných stádií velmi hmotných hvězd. Zde patří k nejzajímavějším příběhům historie fyziky střet Roberta Oppenheimera a Johna Archibalda Wheelera. V článku z února 1939 byla popsána limita pro hmotnost neutronové hvězdy, při jejímž překročení se zhroutí bez ohledu na složení jaderné hmoty a její stavovou rovnici. Ve stejném časopise Physical Review dne 1. září 1939 pak Robert Oppenheimer publikoval společně s kolegou Hartlandem Sweetem Snyderem článek popisující nezadržitelný kolaps příliš hmotné hvězdy pod Schwarzildův poloměr do černé díry. Šlo o první předpověď vzniku černé díry. Využilo se symetrické homogenní řešení Obecné teorie relativity nerotujícího velmi hmotného objektu.

V článku ukázali, že pozorovatel, který se pohybuje s povrchem kolabující hvězdy, spadne pod Schwarzildův poloměr poměrně rychle. Pro pozorovatele, který jej pozoruje vně kolabující hvězdy, se kolaps hvězdy a pád jeho kolegy při přibližování k Schwarzildovu poloměru stále více zpomaluje a překoná jej až v nekonečném čase. Pokud přijímá jim vysílané signály, pozoruje stále větší gravitační rudý posuv, až v nekonečnu signál úplně zmizí.

Einstein a Oppenheimer ve filmu Oppenheimer (zdroj Universal).

Ve stejném čísle Physical Review vyšel i společný článek Nielse Bohra a Johna Archibalda Wheelera o vlastnostech štěpení uranu. Zároveň 1. září 1939 začala druhá světová válka. A právě tento článek a historická událost dramaticky ovlivnily osudy všech zmíněných vědců. Robert Oppenheimer se stal vědeckým ředitelem projektu Manhattan a byl klíčovou osobou vývoje americké jaderné zbraně. Na vývoji jaderné zbraně se podílel i John Wheeler pracoval na separaci plutonia v Hanfordu. Na projektu Manhattan pracoval i George Volkoff, jako celá řada Oppenheimerových studentů.

Ve válce padl bratr Johna Wheelera, ten pak měl možná pocit, že kdyby vývoj jaderné bomby proběhl rychleji a ukončila by válku dříve, nemusel by jeho bratr zemřít. A i proto možná prosazoval s Edwardem Tellerem rychlý rozvoj termojaderné zbraně, na jejímž vývoji se podílel. Zde se střetl s Robertem Oppenheimerem, který byl proti vývoji tohoto druhu bomby. Zároveň zpochybňoval, že by její konstrukce navrhovaná právě Tellerem a Wheelerem vedla k cíli, a předpovídal jejich neúspěch. Po podrobnějším prostudování jejich návrhů však názor změnil.

Robert Oppenheimer se už nikdy k výzkumu konečných stádií hvězd a černých děr nevrátil. Naopak John Wheeler se stal v oboru černých děr a Obecné teorie relativity veličinou. Stal se také tvůrcem pojmenování objektu černá díra. Navázal i na práci Roberta Oppenheimera o kolapsu velmi hmotných hvězd do černé díry. Nevěřil, že je jejich výsledek je správný. Podle něj byl izotropní a homogenní model příliš velkým zjednodušením a existující fluktuace by měly kolapsu pod Schwarzildův poloměr zabránit. Podrobnější a komplexnější výpočty pomocí programů Tellera, které vypracovali při cestě za termojadernou bombou, potvrdily nevyhnutelnou realizaci kolapsu a vzniku černé díry. A John Wheeler svůj názor změnil.

Limitní hmotnost ovlivňuje stavová rovnice dané formy jaderné hmoty

Přibližný tvar dvounukleonového potenciálu silné jaderné interakce.

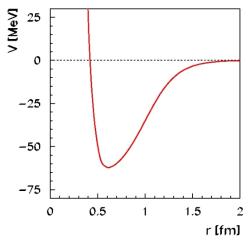
Jak jsme psali, je potenciál interakce mezi dvěma nukleony na vzdálenost okolo jednoho femtometru přitažlivý, na krátkou vzdálenost, menší než 0,5 fm je však odpudivý. V nitru neutronových hvězd může být hustota jaderné hmoty až desetkrát vyšší než v jádře. Nukleony jsou tak tam mnohem blíže k sobě a odpudivá komponenta silné jaderné interakce zvyšuje odolnost objektu vůči kolapsu. Přesný tvar potenciálu a vlastnosti silné jaderné interakce udávají stavovou rovnici této hmoty, odolnost vůči kolapsu, a tedy i konkrétní limitní hmotnosti neutronové hvězdy

U neutronové hvězdy gravitační pole vede k vysoké Fermiho energii. V tom případě je tak dostatek energie pro přeměnu neutronu na těžší hyperon lambda. V nitru neutronové hvězdy by tak mohla být hyperonová hmota. Podle našich znalostí potenciálu interakce hyperonů by to mělo vést ke „změkčení“ stavové rovnice a snížení maximální možné hmotnosti neutronové hvězdy.

Jaká hmota je v nitru neutronové hvězdy

Hmotou v nitru neutronové hvězdy tak nemusí být pouze neutrony, ale i hyperony, zvláště lambda. Dále by se tam mohl nacházet mezonový kondenzát. Mezony jsou bosony a je pravděpodobné, že i mezonová stavová rovnice bude „měkčí“ a tato materie sníží limitní hmotnost neutronové hvězdy.

Experiment STAR na urychlovač RHIC v laboratoři BNL publikovali v roce 2023 první pozorování toků hyperjader ve srážkách těžkých jader (zdroj BNL).

Pro ještě vyšší baryonové hustoty se hadrony, které tvoří jadernou hmotu, přiblíží natolik, že kvarky, které je tvoří, ztratí identifikaci s jednotlivými hadrony. Pro dostatečné hustoty a teploty pak může dojít k přechodu hadronové hmoty do fáze kvark-gluonového plazmatu. V tomto případě je jaderná hmota tvořena z volných kvarků a gluonů, což jsou částice, které zprostředkují silnou interakci. Odolnost neutronové hvězdy proti kolapsu pak určuje stavová rovnice kvark-gluonového plazmatu.

Extrémně důležité pro pochopení vlastnosti neutronových hvězd je znalost stavové rovnice jaderné hmoty různého složení a v různé fázi, a také znalost jejího fázového diagramu, který popisuje podmínky (teploty a baryonové hustoty) při kterých dochází k přechodu mezi různými fázemi. Tyto vlastnosti lze studovat i v pozemských laboratořích.

Jak se studuje velmi hustá jaderná hmota?

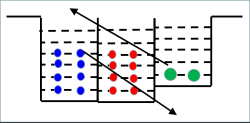
Jadernou hmotu, která se vyskytuje v neutronových hvězdách, je možné připravit i v pozemských laboratořích pomocí srážek těžkých jader s relativistickými rychlostmi blízkými rychlosti světla. Při srážce vzniká velmi hustá jaderná hmota. Pokud jsou urychlená jádra ultrarelativistická a jejich kinetická energie je řádově vyšší, než je jejich klidová energie, bude mít hmota vzniklá při srážce kromě vysokých hustot i velmi vysoké teploty. Velká část kinetické energie se přemění i na klidovou energii nových částic, které vznikají ve dvojicích částice a antičástice. Ty budou mít také velice vysokou kinetickou energii. Původní srážející se jádra jsou z hmoty, a tedy baryonů. Po srážce sice naroste hustota energie i hustota částic. Ale dominantně půjde o dvojice částice a antičástice. Relativní podíl přebytku baryonů se tak stává velmi malým. Taková hmota je podobná té, která byla na počátku našeho vesmíru.

Budované urychlovačové centrum FAIR v německém Darmstadu (zdroj GSI Darmstadt).

Při nižších energiích se dramaticky zvyšuje baryonová hustota, nových částic v párech částice a antičástice vzniká méně, relativní přebytek baryonů tolik neklesá, a navíc jsou stlačovány k sobě. Nestoupne také tolik teplota jaderné hmoty. Taková hmota je blízká relativně chladné hmotě neutronových hvězd.

Čerenkovův detektor identifikující lehké nabité částice pomocí Čerenkovova záření je srdcem spektrometru HADES (zdroj V. Wagner).

Jedním ze zařízení, která se zaměřují na studium této „chladné“ jaderné hmoty s vysokou baryonovou hustotou, jsou zařízení v laboratoři GSI Darmstadt v Německu, která využívají urychlovač SIS. Zde se nyní buduje daleko větší a komplexnější zařízení FAIR. Pomocí něj by se měly studovat i vlastnosti hyperonů a hyperjader. Do těchto výzkumu jsme prostřednictvím experimentu HADES, který už řadu let získává data, a experimentu CBM, který se buduje pro zařízení FAIR, zapojeni i fyzikové z našeho ústavu a podílím se na nich i já. HADES je spektrometr, který je dominantně zaměřen na mezony rozpadající se na pár elektronu a pozitronu. Některé jsou velice krátce žijící a rozpadají se uvnitř velmi husté hmoty. Elektrony a pozitrony neinteragují silnou interakcí, nejsou tak při průletu hustou hmotou ovlivněny a nesou tak plnou informaci o mateřských částicích. Jejich vlastnosti, například hmotnost, jsou ovlivněny médiem, ve kterém se nacházejí. Nesou nám tak informaci o něm.

Principem femtoskopie je studium korelace dvojice částic v závislosti na rozdílu jejich hybnosti. Poměr počtu korelovaných a nekorelovaných dvojic v závislosti na rozdílu hybnosti dvojice částic závisí na tom, jestli je interakce mezi nimi přitažlivá nebo odpudivá (prezentace V. Mantovani Sarti na konferenci Quark Matter 2021).

Vývoj v této oblasti dost silně ovlivnila invaze Ruska na Ukrajinu. V SÚJV Dubna se buduje podobné zařízení, jako je FAIR. Systém urychlovačů a detekčních sestav NICA se zaměřuje na trochu jiné energie a obě zařízení se velmi dobře doplňují a panuje mezi nimi významná synergie. Proto byla velmi intenzivní spolupráce a dělba práce v mezinárodní komunitě při budování obou zařízení. Vzájemně si dodávala různé komponenty. Česká republika byla velmi intenzivně zapojena do obou projektů. Po invazi Ruska na Ukrajinu se spolupráce zastavila, Česká republika z SÚJV Dubna vystoupila a přestaly vzájemné dodávky komponent. Oba projekty tak musely hledat jiné dodavatele a čelí tak významným zpožděním. Podrobněji jsem o dopadech invaze Ruska na Ukrajinu na vědu a odchodu České Republiky z SÚJV Dubna psal v článku pro časopis Vesmír.

Celá řada experimentů na velkých urychlovačích, jako je zmíněný SIS v GSI Darmstadt, LHC v laboratoři CERN a RHIC v americkém Brookhavenu studuje vlastnosti horké a husté jaderné hmoty. Snaží se detekovat co nejvíce částic vznikajících v různých fázích srážky těžkých jader a určovat jejich parametry. Z nich pak dokážou určovat složení, teplotu, hustotu a tlaky v jaderné hmotě v měnících se podmínkách. Několik článků popisujících studium velmi husté jaderné hmoty umožňující poznat vlastnosti vývoje vesmíru a konečných stádií hvězd jsem psal pro časopis Vesmír (zde, zde, zde a zde). Popisují se zde metody výzkumu stavové rovnice jaderné hmoty pro různé její složení i fáze a také dosažené výsledky.

Korelační funkce pro různé dvojice částic u srážek dvojice protonů s energií dostupnou v těžišti 7 TeV (Zdroj: ALICE collaboration: arXiv:1805.12455v3).

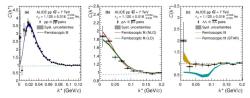
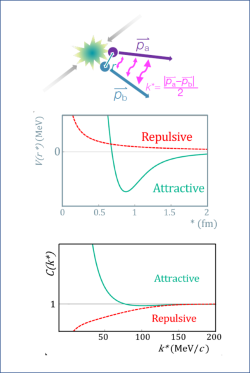
Zde se podívejme na jednu zajímavou možnost pozorování, která umožňuje zjistit vlastnosti interakce mezi nukleony a hyperony. Jde o femtoskopii různých částic, a zvláště pak hyperonů. Pokud částice vzniknou nebo se octnou blízko sebe, bude jejich další chování silně záviset na tom, jestli je jejich vzájemná interakce přitažlivá nebo odpudivá. Pokud je jejich potenciál odpudivý, bude větší pravděpodobnost, že je nalezneme dále od sebe, pokud bude přitažlivý, bude větší pravděpodobnost je najít u sebe. Zjistíme to studiem korelace dvojice částic. V tomto případě se podíváme na počty dvojic v závislosti na velikosti jejich vzájemné hybnosti. A to v případě, že jde o korelované dvojice a dvojice nekorelované. V prvním případě jde o dvojice ze stejné srážky a v druhém případě pak o dvojice částic z různých srážek. Podíl korelovaných a nekorelovaných dvojic v oblasti blízkých hodnot hybnosti je v případě odpudivého potenciálu menší než jedna a v případě přitažlivého potenciálu pak větší než jedna.

Vývoj teploty neutronové hvězdy s jejím stářím. Ta postupně klesá, až se dostane pod teplotu v nitru Slunce.

Velice zajímavé výsledky studia s využitím femtoskopie byla získána pomocí urychlovače LHC a experimentu ALICE. Zde se při srážkách protonů studovala femtoskopie dvojice nukleonů, páru nukleon a lambda a dvojice lambda. Ukazují se významné rozdíly mezi korelačními funkcemi v případě různých dvojic. První výsledky ukazují, že jde o velmi perspektivní metodu, která by mohla osvětlit průběh interakce mezi hyperony a nukleony a vyřešit hyperonovou hádanku.

Vznik a vlastnosti neutronových hvězd

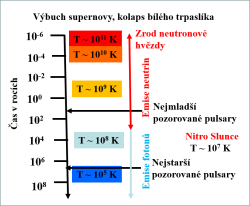
Teď se podrobněji podívejme na vznik a vlastnosti neutronových hvězd, a co se můžeme z jejich pozorování dozvědět o vlastnostech jaderné hmoty, která je tvoří. Pokud hmotnost hvězdy překračuje určitou hraniční hmotnost a nedokáže ji během konečných stádií snížit, vybuchne jako supernova a její nitro zkolabuje do neutronové hvězdy. Tedy z poloměru v řádu 700 000 km na zhruba 10 km. Protože se zachovává moment hybnosti, doba rotace, která je u normální hvězdy v řádu desítek dní, se zkrátí až na desítky milisekund. Stejně tak kolapsem rozměrů naroste velikost magnetické indukce z hodnot v řádu desetin tesla až na řády miliard tesla. Počáteční teplota v nitru neutronové hvězdy je 10¹¹ K. Připomeňme, že teplota v nitru Slunce je 10⁷ K. Teplota poměrně rychle klesá a po roce se dostává pod řád 10⁹ K. Během miliónu let klesne až na 10⁵ K.

Neutronová hvězda v dvojhvězdném systému s červeným obrem. Dochází k přetoku hmoty, emisi rentgenova záření a urychlování rotace neutronové hvězdy (zdroj NASA).

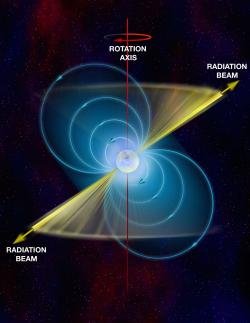
Rychlá rotace a velmi intenzivní magnetické pole způsobují, že se neutronová hvězda projevuje jako pulsar. Magnetické pole ovlivňuje pohyb nabitých částic, hlavně elektronů, a vytváří jejich proudy, které vytvářejí emise elektromagnetického záření emitované zhruba ve směru magnetické osy neutronové hvězdy. První pulsary se pozorovaly pomocí radiových vln. Magnetická osa je vůči rotační skloněná. Při rotaci tak kužel rádiových vln zametá prostor, a pokud je vhodná geometrie, zasáhne i Zemi. Naše radioteleskopy tak vidí pravidelné pulsy pozorovaného pulsaru. Taková pozorování nám přináší celou řadu velice důležitých informaci o neutronových hvězdách.

Elektromagnetickou emisi pulsaru způsobuje jeho magnetické pole a rotace (zdroj B. Saxton, NRAO/AUI/NSF).

Pozorujeme, že rotace se u neutronové hvězdy v čase zpomaluje a z milisekund se doba rotace prodlužuje do několika sekund. Je to dáno tím, že neutronová hvězda vyzařuje energii, nejdříve hlavně pomocí neutrin a později hlavně fotony. Postupně se tak také snižuje teplota neutronové hvězdy a intenzita magnetického pole. Nakonec zhruba po desítkách milionů let přestane neutronová hvězda vyzařovat radiové vlny a přestane být pulsarem. Starší neutronové hvězdy je tak extrémně náročné pozorovat.

Na základě rychlosti rotace lze odhadovat stáří pulsaru. Neplatí to v případě tzv. milisekundových pulsarů. Ty se vyskytují ve dvojhvězdě, kde je druhou složkou rudý obr, ze které přetéká hmota na neutronovou hvězdu. Ten přináší i moment hybnosti a zrychluje rotaci pulsaru. Jejich doba rotace tak dosahuje až zlomku milisekundy. Pozorují se taky skoky v rotaci, které svědčí o komplikované vnitřní struktuře neutronové hvězdy.

Jak se určují hmotnosti neutronových hvězd?

Pokud chceme srovnávat rozměry a hmotnosti neutronových hvězd s předpovědí modelů, musíme je měřit. To není jednoduché. Jednou z možností určit hmotnost neutronové hvězdy je, pokud se vyskytuje ve dvojhvězdě. Pohyb složek hvězdy ve dvojhvězdě umožňuje určit jejich hmotnosti.

Pro určení rozměrů a hmotnosti neutronové hvězdy lze využít podrobná analýza měření jejího rentgenového záření. Ve vesmíru pracuje několik observatoří zaměřených na rentgenové záření. Velmi zajímavý rentgenový dalekohled pracuje od roku 2017 na mezinárodní vesmírné stanici ISS. O tomto zařízení NICER (Neutron star Interior Composition Explorer) a jeho využití při studiu nitra neutronových hvězd se podrobně píše v dřívějším článku. Teleskop umožňuje velice přesné určení příletu fotonu u teleskopu NICER. Lze tak velice přesně analyzovat průběh změny intenzity rentgenového záření během rotace neutronové hvězdy. To, jaké je zakřivení prostoročasu v blízkosti povrchu neutronové hvězdy a tím i průběh změn intenzity rentgenového záření závisí na hmotnosti hvězdy a jejím poloměru. Pokud hmotnost neutronové hvězdy známe, můžeme z průběhu změn intenzity rentgenového záření během její rotace určit její rozměry. S využitím pozorování pulsarů, které se vyskytují ve dvojhvězdách, se podařilo určit hmotnost několika doposud nejtěžších pozorovaných neutronových hvězd a jejich rozměr. V roce 2019 byla zjištěna hmotnost pulsaru PSR J0740+6620, který je ve dvojhvězdě s bílým trpaslíkem. Jeho hmotnost byla určena na hodnotu 2,08(7) M_S a poloměr 12,4 (10) km. Ještě těžší pulsar byl identifikován v roce 2022. Jde o PSR J0952-0606, jehož hmotnost je 2,35(17) M_S. V tomto případě je jeho souputníkem hnědý trpaslík nebo velká planeta.

Na přelomu roku 2023 a 2024 se intenzivně diskutoval nově objevený zajímavý systém s milisekundovým pulsarem PSR J0514-4002E a druhým kompaktním objektem s hmotností mezi 2,1 -2,7 MS, o kterém se zatím neví, jestli jde o neutronovou hvězdu nebo černou díru (zdroj MPIfR; Daniëlle Futselaar (artsource.nl))

Velice zajímavé informace o hmotnostech a vlastnostech neutronových hvězd by mohly přinést pozorování gravitačních vln vzniklých ve splynutí dvou neutronových hvězd. Zatím se podařilo pozorovat pouze dva případy této události. První pozorování gravitačních vln ze splynutí neutronových hvězd je popsáno v článku z podzimu roku 2017. Zároveň šlo o nejbližší pozorovaný krátký záblesk gama. Pozorování se podařilo v téměř celém rozsahu elektromagnetického spektra. Šlo o potvrzení, že přinejmenším za velkou částí krátkých záblesků gama je splynutí neutronových hvězd.

Po splynutí dvou neutronových hvězd vzniká podle hmotnosti produktu tohoto splynutí vznikne buď těžší neutronová hvězda nebo vzniklý objekt zkolabuje do černé díry. Může dojít i k tomu, že napřed vznikne neutronová hvězda a teprve po snížení její teploty nebo transformace její hmoty do jiné fáze nebo typu částic dojde ke kolapsu neutronové hvězdy do černé díry. I průběh emise gravitačních vln a jejich vlastnosti je dán tím, jaké vlastnosti mají neutronové hvězdy a jak se během splynutí mění. Přesné pozorování emise gravitačních vln tak umožňuje zjistit vlastnosti nitra neutronových hvězd.

Vztah mezi hmotností a poloměrem neutronové hvězdy pro různá složení neutronových hvězd. Je vidět, že příměs hyperonů vede ke snížení maximální možné hmotnosti. Jsou zde různé varianty potenciálů hyperon-nukleonové interakce. Červená křivka označuje výpočty s využitím pouze dvoučásticového potenciálu, modrá pak započítává i tříčásticové síly. Jsou zde vyznačeny i hmotnosti nejtěžších pozorovaných pulsarů PSR J0348+0432 a PSR J1614-2230. (Zdroj Lonardoni et al: Phys. Rev. Lett 114, 092301 (2015))

Jak bylo zmíněno, zatím byl pozorován jen velmi malý počet splynutí neutronových hvězd. Je to dáno tím, že signál v podobě gravitačních vln při splynutí neutronových hvězd je mnohem slabší, než je tomu v případě splynutí černých děr. Vidíme je tak do omezené vzdálenosti, opravdu jen ty nejbližší. Zlom by mohla přinést nová generace detektorů gravitačních vln. Takovým by měl být i plánovaný evropský Einsteinův teleskop gravitačních vln, který je podrobněji popsán v dřívějším článku.

Závěr

V posledních letech se daří díky novým rentgenovým vesmírným teleskopům určovat hmotnosti a rozměry rostoucího počtu neutronových hvězd. Daří se nacházet i velmi hmotné neutronové hvězdy s hmotností vyrovnávající i překračující hodnotu 2 M_S. To je však hodnota vyšší, která už je velmi blízko nebo dokonce rovná hraniční hmotnosti složené z neutronové hmoty. Podle současných znalostí by se však v nitru hvězd měla nacházet hmota složená z lambda hyperonů. Naše dosavadní znalosti o interakci lambda hyperonů mezi sebou a s nukleony vedou k představě, že se tato hraniční hmotnost neutronové hvězdy sníží a modelová je tak nižší, než jsou hmotnosti nejtěžších známých pulsarů. Tento rozpor se označuje za hyperonovou hádanku.

Její vyřešení může být realizovanou upřesněním a změnou našich představ o interakci nukleonů a hyperonů, které povede k vyšším hodnotám limitní hmotnosti v modelech neutronových hvězd. Na to se zaměřují studie s využitím urychlovačů relativistických těžkých iontů, které umožňují vytvořit a analyzovat velmi hustou jadernou hmotu. Stejně tak mohou pomoci experimenty s produkcí hyperjader a studiem jejich spekter. Analýza získaných dat by měla upřesnit popis silné interakce mezi hyperony a nukleony včetně vícečásticových sil.

Mohlo by se také ukázat, že je chyba v naší metodice určování hmotnosti neutronových hvězd a ve skutečnosti neutronové hvězdy s hmotností dvě hmotnosti Slunce a více neexistují. Zde je důležitý pokrok v oblasti pozorování vlastností pulsarů a gravitačních vln ze splynutí neutronových hvězd.

V obou zmíněných oblastech se dá v nejbližších letech čekat významný pokrok a lze očekávat, že se hyperonovou hádanku podaří již brzy vyřešit.

Video: Přednáška o studiu hmoty v nitru neutronových hvězd a hyperonové hádance pro Fyzikální čtvrtky FEL ČVUT

Video: Přednáška o Oppenheimerovi a rozdílu mezi filmem a skutečností pro Café Nobel UJEP

Video: Přednáška o femtoskopii hyperonů a studiu hmoty uvnitř neutronových hvězd pro TEDxTUM od kolegyně z experimentů HADES a ALICE od Laura Fabieti