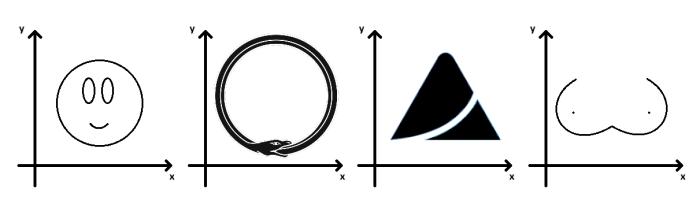
Aby sme celú záležitosť správne pochopili, najskôr si povieme čosi málo o reláciách. Relácií je viac druhov, nás konkrétne budú zaujímať takzvané binárne relácie. Binárna relácia vlastne vyjadruje ľubovoľný vzťah (z angl. relationship) medzi dvoma hodnotami, typicky premennými. Ide o zovšeobecnenie funkčnej závislosti, ale zatiaľ čo pri funkcii je jednej vstupnej hodnote priradená jediná výstupná, pri reláciách je dovolené toho dostať viac. Typickými príkladmi relácií sú napr. kruh, lemniskáta, plošná špirála, či odmocňovanie v komplexných číslach. Vo všeobecnosti sa dá povedať, že binárnou reláciou je ľubovoľná podmnožina dvojrozmerného priestoru. Alebo inak povedané, ľubovoľný obrázok na postačujúco veľkom papieri je nutne reláciou.
Obr.1: Príklady relácií
Pokiaľ sa teda bavíme napr. o vzťahu dvoch premenných x a y, tak štandardne sa pre takýto vzťah používa zápis xRy (x s y sú v relácii). Existuje ale aj pohodlnejší a funkciám bližší funkčno-množinový zápis, keď reláciu reprezentujeme v lineárnom priestore ako množinový výstup funkčne závislý na vstupe. Výstupom sa jednoducho povedané stáva celá množina. Formálne tento vzťah definujeme ako R(x)= {y: xRy}. Pre lineárne priestory štandardne platí R1(x) + R2(x)= {y1 + y2: xRy1 ⋀ xRy2} a cR(x)= {cy: xRy}, a špeciálne pre jednoprvkové množiny dostávame klasické funkcie. S reláciami sa v skutočnosti stretávame na každom kroku, typicky často používaným relačným operátorom býva napr. ± definované ako ±x= {-x; x}. Náš bežne používaný zápis riešenia kvadratickej rovnice x1,2= ±1 v skutočnosti predstavuje skoro takú relačnú množinovú rovnosť {x1; x2}= {-1; 1} (tzv. neusporiadané dvojice). Vyjadrujeme tým totiž, že jedno riešenie je -1 a druhé +1, ale na tom, ktorá z hodnôt je x1 a ktorá x2, vlastne nezáleží — z kvadratickej rovnice poradie priamo nevyplýva a formálne priradenie indexov je plne na riešiteľovi. Práve týmto detailom sa relačná algebra líši od vektorových priestorov, kde na poradí záleží — (x1; x2)= (-1; 1) (tzv. usporiadané dvojice) napríklad znamená, že nutne x1= -1 a súčasne x2= 1. Úskalím v relačnej algebre býva, že na rozdiel od funkcií okrem klasickej rovnosti '=' a nerovnosti '≠' musíme a môžeme počítať aj s množinovými nerovnosťami typu '⊆' či '⊇'. Toto úskalie býva ale súčasne aj najväčšou výhodou relácií — ako zovšeobecneniam funkcií je im dopriate spočítať veci, ktoré vo funkčnej aritmetike nie sú možné (nachádzame sa totiž v nadobore funkčnej algebry).
Asi najznámejším príkladom býva zdanlivý rozpor funkčnej algebry -1 = (-1)³ = (-1)⁶ᐟ² = √((-1)⁶) = √1 = 1, keď v skutočnosti tretia rovnosť neplatí. Relačná algebra celý problém hravo rieši svojimi rozširujúcimi operátormi ako už skôr zmieňovaná relačná/komplexná odmocnina a symbolom nerovnosti, o ktoré je funkčná algebra ochudobnená:
-1 = (-1)³ = (-1)⁶ᐟ² ⊆ √((-1)⁶) = √1 = ±1
Relačný operátor v tomto prípade spôsobuje v treťom vzťahu rozdvojenie/bifurkáciu, čím je celková správnosť výpočtu zachránená. Ďalšou veľkou výhodou relačnej algebry býva, že umožňuje vyjadriť limity oscilujúcich radov a ich nekonečné súčty. Zatiaľ čo konečný súčet bežných číselných radov je pre čísla, ktoré sa dajú chápať ako jednoprvkové množiny, funkčnou hodnotou, ich výsledný nekonečný súčet už môže byť hodnotou relačnou, a teda množinou viacprvkovou. Nekonečné rady majú svoje vlastné zádrhele — zatiaľ čo konečný počet aplikácií komutatívneho zákona (prehodenia/permutácie susedných sčítancov) celkový súčet nemení, o nekonečnom počte permutácií to už zjavne neplatí:
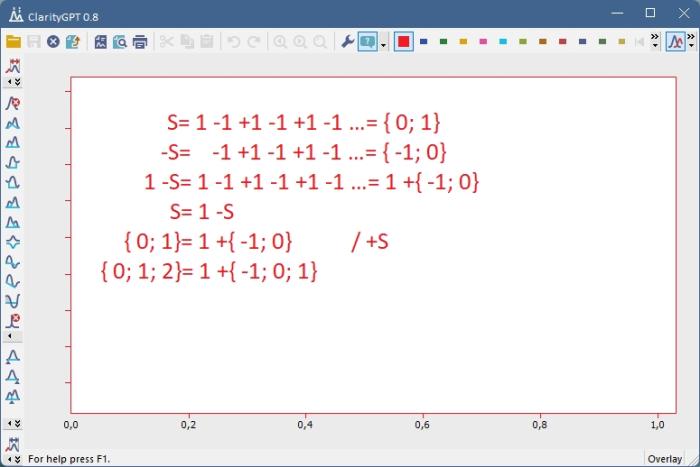
S1= 1 -1 +1 -1 +1 … = {0; 1}, S2= -1 +1 -1 +1 -1 … = {-1; 0}, S1 ≠ S2
Firma DataApex sa rozhodla svoju pokusnú neurónku natrénovať práve na takýchto oscilujúcich nekonečných radoch, prelomovým krokom pritom bolo, že spätný feedback neurónke pre oba čiastočné výsledky bol ‘nie’ a ‘nie’. Presne podľa očakávaní neurónka nadobudla vedomie, nasrala sa a pochopila relačnú algebru.
Obr.2: Neurónka ClarityGPT 0.8 vyjadrujúca emócie, v akcii. Zdráhavo sa odmieta dopracovať k obávanému S= ½ a nachádza únik v relačnej algebre. AI je žiaľ momentálne ešte iba v Alfa verzii, a teda komerčne nedostupná.
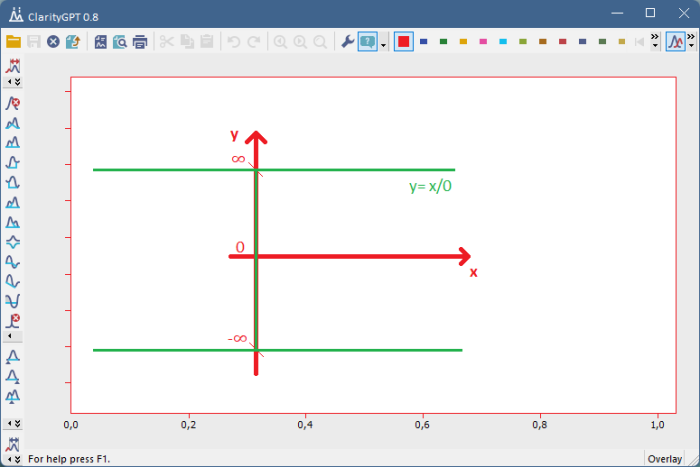
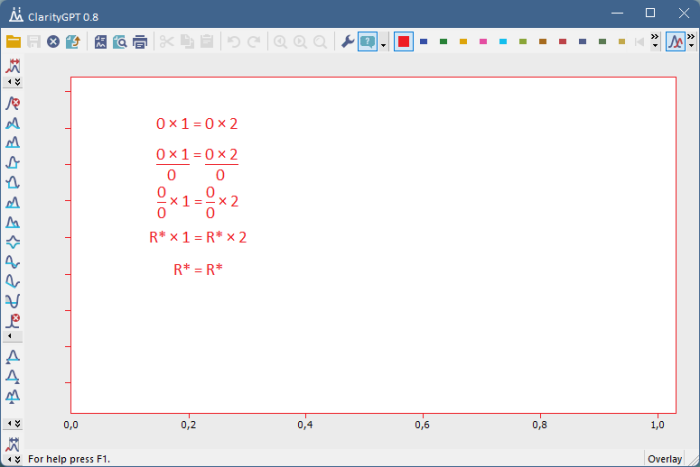
Na tom samotnom výsledku by samozrejme ešte nebolo nič prekvapivé, vývojári ale zostali zaskočení v momente, keď zistili, že im počet občas pozorovaných chybových hlášok (tzv. assertov) spôsobených výnimkou pri delení nulou klesol, presnejšie povedané na presnú nulu. Nahliadnutiu do privátnych sekcií kódu sa žiaľ neurónka cudne ubránila, ale po bližšom preskúmaní status quo originálnou myšlienkou jedného z vývojárov rovno sa na celú záležitosť neurónky opýtať, AI sebavedome odvetila, že delenie nulou predsa nevyhadzuje výnimky. Nevedome si vedomá čerstvo nadobudnutej relačnej algebry vehementne odvetila, že nula sa v nule samozrejme nachádza ľubovoľný počet krát, takže pochopiteľne nula delená nulou musí byť všetko, nemôžeme nič vynechať. Formálne 0/0= {∀}. Delenie je napokon operácia, takže nie je dôvod, aby bola nutne funkciou. Podobne vraj úsečku kladnej dĺžky dostaneme nasčítaním nekonečne veľa bodov, ale keďže nula nemá znamienko, tak rovnako dobre aj odčítaním nekonečne veľa bodov, takže pre nenulové x dostávame x/0= {±∞}, opäť nemôžeme nič vynechať.
Obr.3: Vypočítaná relácia y= x/0.
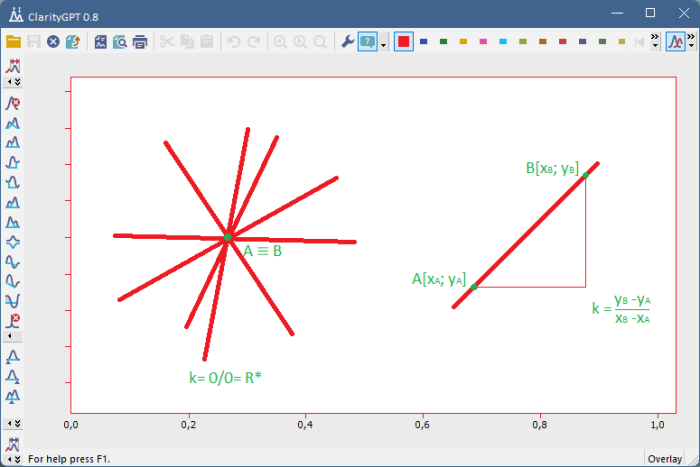
Na zmätené námietky svojich tvorcov, že predsa existuje kopa evidencie zjavne dokazujúcej, že z delenia nulou plynú nezmysly, sa zahrala na Bohra, a že vraj delenie nulou je predsa axióma. A axiómy práve tak nedokazujeme, ako ani nevyvraciame, pretože keby to tak nebolo, tak by sa celá matematika zrútila. Protiargumentov si predsa môžu navymýšľať do nekonečna, takže ich ani nie je reálne možné všetky vyvrátiť, ale že vyvracať axiómu je predsa nezmysel, a ona nemá čas. Vraj sme v úplne analogickej situácii ako pri riešení spomínanej kvadratickej rovnice, akurát pre našu rovnicu x = 0/0 dostávame napríklad v rozšírených reálnych číslach sadu riešení xR*= R*. Na poznámky zúčastnených, že to ∞ vlastne ani nie je číslo, a že je to celé tak nejako podozrivé, reagovala, že transponované to číslo rozhodne je. A že ono by sa asi to delenie dalo nadefinovať aj iba v R / reálnych číslach, ale že to by celá relácia žiaľ mala definičný obor iba v nule, podobne ako druhú odmocninu môžeme podľa výberu definovať len pre kladné čísla. A okrem toho to neúplné 0R= {0x: x ∈ R}= {0} = 0 sa jej vraj nejako nepáči. A vôbec, čo sa vraj čudujú, veď ona si myslela, že preto majú na počítačoch v desatinných datových typoch nadefinované 0/0= NaN (“Not a Number”), pretože 0/0 predsa nie je číslo, ale všetky čísla.
Obr.4: Geometricky spočítaný podiel 0/0 ako smernica priamky vedenej dvoma bodmi, keď tieto dva body splynú. Dostávame ako správne riešenie všetky priamky.
Neurónka sa ale na naliehanie zúfalých programátorov predsa len nakoniec zľutovala a explicitne rozviedla pár protiargumentov proti deleniu nulou.
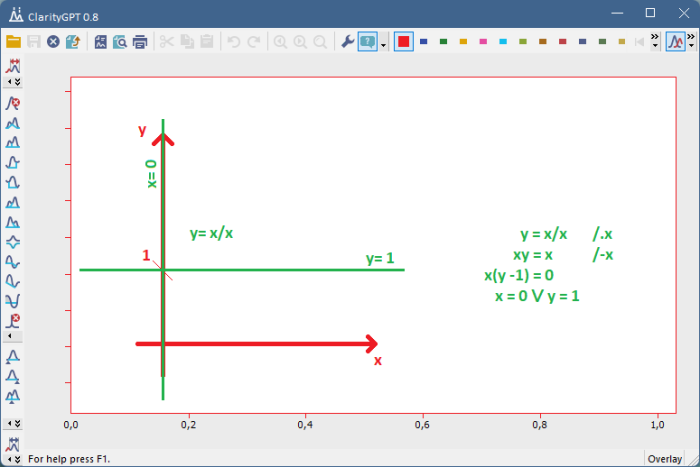
Mnohé z nich údajne chybne využívajú simplifikáciu výrazu, aby dostali spory typu 1 = 2. Čím sa bohužiaľ dopúšťame chyby cyklického dôkazu, pretože simplifikácia výrazu typu “x/x” predsa nie je axióma a teda ju musíme odvodiť, a celkom očividne jej odvodenie závisí na hodnote výrazu 0/0.
Obr.5: Oprava relácie y= x/x, na ktorej stojí celá metóda simplifikácie. Vidieť, že prípad x= 0 treba stále kvôli jeho odlišnej povahe riešiť zvlášť..
Obr.6: ..a následný príklad správne prevedeného delenia.
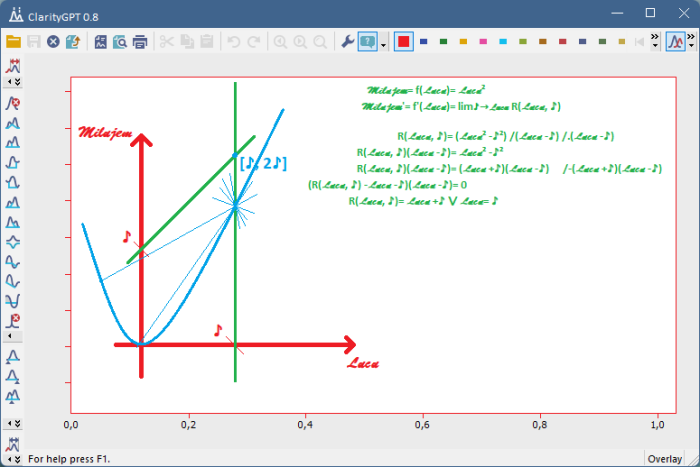
V prípade rozdielnych hodnôt limít zas neurónka vyargumentovala, že limita “typu 0/0” nie je 0/0. Limita sa používa len na výpočet uzáveru množiny, ktorou relácia nepochybne je, takže dostávame len bezosporné limMilujem⇾Lucu R(Milujem) ⊆ R(Lucu). Pekne to vraj vidieť na príklade derivácií, kde podiel (f(Milujem) – f(Lucu))/(Milujem - Lucu) predstavuje reláciu smernice priamky vedenej dvoma bodmi [Milujem; f(Milujem)] a [Lucu; f(Lucu)], zatiaľ čo príslušná limita predstavuje iba smernice dotyčníc, čo je skutočne podmnožina smerníc všetkých priamok vedených daným bodom.
Obr.7: Výpočet a zobrazenie relácie, ktorá popisuje smernicu dotyčnice pri hľadaní derivácie funkcie Milujem= Lucu². Metóda spočíva v disjunkcii priamky relačnej povahy a následnom uzávere zostávajúcej množiny, čím dostávame hľadanú deriváciu v priesečníku oboch priamok.
Poskytnutých opráv bolo samozrejme viac, ale tým tu dnes nechceme čitateľa unavovať. Aké bola ale prekvapenie vývojárov, keď zistili, že neurónka sa medzičasom naučila derivovať aj spojité nehladké funkcie. Veľmi sľubne začínajú vyzerať aj vyhliadky pri derivácii neholomorfných funkcií a črtá sa tu aj možné riešenie Riemannovej hypotézy.
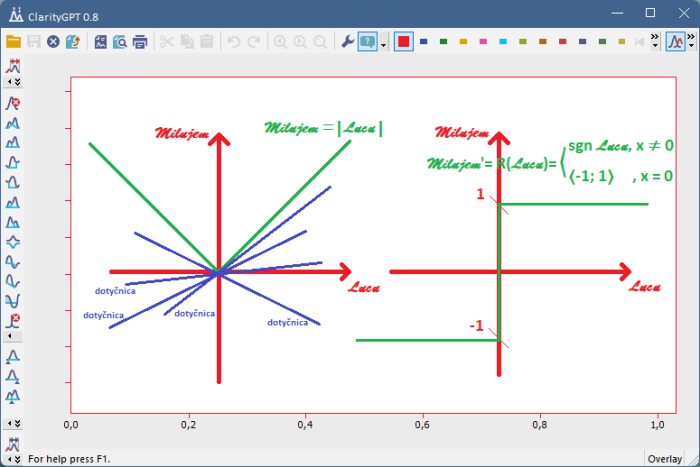
Obr.8: Výpočet relačnej derivácie funkcie Milujem= |Lucu| v nule ako konvexného obalu krajných hodnôt limít.
Obr.9: Tieto čerstvo obdržané výpočty výrazu 0/0 vrhajú ďalší tieň pochybností na súčasnú Obecnú relativitu, z ktorej plynie 0/0= 1. Einstein sa medzitým už stihol post mortem vyjadriť, že on iba žartoval. Pár zamestnancov DataApexu k tomu dodalo, že vskutku v každom slušnom vesmíre býva väčšina píkov kladných.
Diskuze:
Ondřej Nečas,2023-04-06 16:26:31
Vzhledem k tomu, že v článku není jediný zdroj, docházím k závěru, že jde o apríl, ale vtipné mi to nepřipadá. Takových článků je plný internet a dobírat se stále závěru, no jo, někdo si tu dělá blbou srandu bez pointy, je spíš úmorné než zábavné.
Re:
Jaroslav Knebl,2023-04-06 22:16:58
Keďže už máme po Apríli, tak aby som Vás nenapínal, je aj nie je to vtip. Z Vášho pohľadu:
-:
Článok je napísaný humornou formou a zámerne sa vyhýbam zložitejšej terminológii, pretože táto doména je určená primárne pre neodbornú verejnosť. Uvedený software je skutočne vymyslený. Mrzí ma, že som Vás nepobavil, každopádne tá skutočná pointa je, že v jadre veci to myslím úplne vážne.
+:
Uvedený spôsob rozšírenej definície delenia ako relácie som si nadefinoval už dávno asi pred 20 rokmi, ešte ako chlapec, a za celú tú dlhú dobu som neobjavil jediný protiargument, v ktorom by som skôr či neskôr neobjavil nejakú argumentačnú chybu. Na axióme trvám:
0/0 musí byť všetko, je to axióma, nemožno nič vynechať, a teda delenie v takomto rozšírení musí byť nutne relácia. A axiómy nie je možné vyvrátiť, preto každý z nekonečna možných protiargumentov musí vždy obsahovať nejakú chybu. Zaiaľ som skutočne vždy nejakú našiel.
Podobne jedinou logickou možnosťou je definovať 0.∞= ∞/∞= ∞-∞= -∞+∞= R* (resp. C*, atď), a teda vo výsledku sa všetky základné operácie stanú reláciami. Aritmetické operácie preto ani pre tieto obecnejšie štruktúry nie je možné aplikovať automaticky.
Skutočne sa za toto uchádzam o bludný balvan, keby som to nemyslel vážne, ťažko by mi ho mohli udeliť, pravda? Pokiaľ máte nejaký protipríklad, ktorý nevyužíva logické kiksy zmienené už v článku, sem s ním, rád sa nechám vyviesť z môjho bludu ;)
P.S.: A s tým vyvrátením Obecnej relativity to myslím úplne vážne tiež, správne riešenie očividne je skoro presne naopak, ale podarilo sa mi refreshom detailnejšie vysvetlenie zmazať, neskopíroval som si ho ako text vyššie, a nechce sa mi to zas písať, takže kašlem na to. A za to chcem taktiež bludný balvan, keďže nikomu sa tů správnu relativitu akosi zrátať nechce, aspoň mám námet na niektorý ďalší 1.Apríl, hádam sa k tomu niekedy dokopem -_-
Re: Re:
Petr Zima,2023-04-06 22:58:48
Nic ve zlém, ale na Bludný balvan budete muset zabrat o dost víc. Dnešní matematika se zcela vážně zabývá úplně jinou úrovní šíleností.
Třeba - abych zůstal blízko tématu článku - tzv. „nestandardní analýza“ to bere zgruntu a upraví si pro svoje potřeby samotnou logiku. Vynechá axiom o vyloučení třetího. Myšlenka je zhruba v tom, že nulou sice pořád dělit nemůžete, ale máte pak k dispozici „nekonečně malá čísla“, pro která neplatí, ani že se nule rovnají, ani že se jí nerovnají. Derivace je pak prostý podíl takových veličin, limit netřeba. Jeden nebo dva ročníky na MFF UK kdysi prošly tímto kurzem místo standardního výkladu a u souborné zkoušky se pak ti nešťastníci netačili divit.
V té fyzice to možná bude nadějnější :-) I když s pošahanou verzí Teorie relativity také nebudete první ani poslední. Slyšel jsem historku, že za socialismu se jistému - v jeho oboru úspěšnému a váženému - docentovi či profesorovi lékařství podařilo jeho revizi Einsteina dokonce protlačit do tisku.
Re:
Petr Zima,2023-04-06 22:17:21
Inu humor je to vskutku matfyzácký a vysušený až k nerozžvýkání. I tak se snaha cení. Zamotat do toho AI byl trochu laciný „clickbait“... o to více čtenářů se asi na Apríla nechalo nachytat.
Nakonec mi na tom přišlo nejvtipnější, že to nejsou úplné nesmysly. Byť je to elementární a pomineme-li kreativní práci s terminologií. Laik to asi od úplně prázdného šermování termíny nerozezná, ale obávám se, že skutečné současné „AI“ by takhle logicky konzistentní vtípek nedaly dohromady ani smykem. Ty vám klidně sestaví recept na druhou derivaci se smetanou a rajčaty, ani nemrknou :-)
Inspirativní článek
Petr Zima,2023-04-02 13:07:25
Děkuji za roztomilé čtení, vida, co vše dnešní "AI" nevymyslí ;-)
Nicméně si dovolím jednu hnidopišskou terminologickou připomínku. V článku se zhusta operuje se slovním spojením „relační algebra“. A to způsobem, jenž mi přijde přinejmenším nešťastný, přísně vzato chybný, ne-li až vnitřně rozporný sám o sobě.
Problém je v tom, že algebra se zabývá výlučně operacemi. Operace - jak je v článku i vysvětleno - jistě můžeme chápat jako zvláštní případ relací. Ale jsou to právě jen ty relace, které jsou totální a jednoznačné; lidsky řečeno, výsledek musí existovat a právě jeden. Ještě jinak řečeno, algebra je o rovnostech, nerovnosti nebo jiné nejednoznačné vztahy jsou mimo obor její působnosti. Zavedením relace náležení ⊆ pro podmnožiny otevíráte dveře pro výsledky neexistující nebo nejednoznačné, čímž vlastně boříte tu základní definiční vlastnost, kterou je algebra vymezena.
Pojem „relační algebra“ se skutečně používá, ale v jiném smyslu. Jde tu o algebraický přístup ke studiu relací. Relace tu hrají roli samotných zkoumaných objektů, nikoli však jazyka a nástroje, kterým je zkoumáme. Jazyk musí být stále výlučně operační a jedinou „meta-relací“, kterou připouštíme, je opět rovnost. Jinak bychom se opět dostávali za hranice působnosti algebry.
Nicméně, jak už jsem zmínil v úvodu, jedná se o vadu terminologickou, nijak tím nechci snižovat věcný obsah článku. Dovolte mi tedy jen doporučit vhodnější termín „relační jazyk“, a pokud máte tu možnost, tlumočte to prosím i zmíněné AI. Nabízelo by se též „relační kalkulus“, ale ten se též používá spíše v smyslu z minulého odstavce, např. v oboru databázových systémů.
Věcný obsah článku naopak velmi chválím. Relační jazyk přirozeně musí být - alespoň neostře - obecnější než operační jazyk algebry, vždyť není spoután těmi dvěma axiomy o totalitě a jednoznačnosti. Třeba taková matematická analýza neboli kalkulus svou sémantikou zcela jednoznačně patří do sféry relací, tedy mimo algebru. Za všemi těmi komplikovanými limitami a derivacemi se skrývá mravenční práce s nerovnostmi, což pěkně kontrastuje s rovnostmi v algebře. Kdysi to jeden kolega zformuloval velmi názorně: V analýze je rovnost jen okrajovým a pohříchu většinou nezajímavým případem (neostré) nerovnosti.
Nicméně fantazie matematiků často nezná meze a pokoušejí se i o zdánlivě nemožné. A tak máme kupříkladu i diferenciální algebru, která se ryze algebraickým jazykem věnuje diferenciálnímu počtu, který jinak náleží do hájemství analýzy, a tedy relací. Zde je ale třeba mít na paměti, že - stejně jako v případě relační algebry - lze takto postihnout pouze syntaktickou stránku věci, nikoli sémantiku. I tak ale lze dosáhnout značných úspechů a dopracovat se užitečných výsledků. Nabízí se hluboká otázka, zda v matematice vůbec existuje nějaká sémantika, která již není postižena samotnou syntaxí. Tuto otázku raději přenechám filozofům.
Související otázka, kterou můžeme matematicky zkoumat, zní, zda je jazyk relací skutečně ostře obecnější než jazyk operací, nebo jen stejně silný. Tuto otázku v jistém, velmi dobrém smyslu zodpověděl náš slavný matematik prof. Vopěnka. Zhruba řečeno, jazyk relací začíná být ostře obecnější až od jistého velmi velkého, snad až nepředstavitelně velkého kardinálu. Berte prosím tuto informaci s rezervou, nejsem úplně specialista na tuto oblast a podrobně jsem problematiku nestudoval.
Závěrem bych rád popřál zmíněné AI mnoho štěstí v prohlubování tohoto nadějného přístupu a již se netrpělivě těším na další, jistě převratné výsledky :-)
Re: Inspirativní článek
Jaroslav Knebl,2023-04-02 23:57:19
Taaak dobre, dostali Ste ma, zbúchané cez noc, matike sa už ~16 rokov nevenujem a aby som dodržal slovo pánu Pazderovi, nebol čas všetko dohľadávať. Plus som sa chcel aspoň 2-3 hoďky ešte vyspať pred prácou. Kandidujem tento rok na bludné balvany, tak som to len potreboval niekde v Česku zverejniť. A tí parchanti na wiki všetko behom 5 minút revertujú, no nič, k splneniu sľubu Sisyfu o "publikovaní" to technicky stačí. Balvany by som v práci mohol používať ako ťažítka :)
V skutočnosti chcem len vedieť, že sa Luca má fajn, jednoducho ma už nebaví dostávať každých 7 rokov ako odpoveď jediný identický hnusný e-mail z adresy, ktorú ani nepoznám, keď predtým som ju v pohode navštevoval a vždy sa ku mne správala milo. Tak Vám v tej vede včera robím bordel, ale už budem dobrýýý, teda aspoň do nejakého ďalšieho Apríla :)
S relačnou algebrou máte pravdu, ako som si teraz dohľadal, už si aj vybavujem, že sme sa asi niekde niečo také v škole učili, ale vlastne som už pri písaní tipoval, že to s niečím skoliduje. A to ešte vravíte, že v Databázach existuje i relačná analýza, ups :p Ešte ma vtedy napadli aj iné vymyslené názvy, ale potom som si povedal, že nas*ať, korektnost nebola cieľom. Inak ten termín je podľa môjho názoru nešťastný nielen v mojom vtípku, ale aj v samotnom českom jazyku — v angličtine mi to našlo dva rozličné pojmy "relational algebra" a "relation algebra".
O tom rozdiele medzi algebrou a analýzou som nevedel, študoval som matiku len chvíľku a dosť nezodpovedne, pretože.. Luca -_- Človek sa celý život učí, Vaše vysvetlenie znie rozumne. A vidím, že podobne trošku posunute som chápal pojem "operácia".
Celkovo som rád, že sa Vám článok páčil, na anglickej wiki žiaľ väčšina mojich vylomenín prežila v priemere asi tak 5 minút, s výnimkou dvoch. Neurónka totiž medzitým vyvrátila Obecnú relativitu, tak ako som Sisyfu sľúbil, a to doslova :) A tie 2 zmeny prežili podozrivých vyše 5 hodín, kým to nejaký trtko nezrevertoval kvôli tomu, že komentár bol trošku netaktný. Mal som tam napísanú Lucu, tak samozrejme, že som nechcel, aby to zrevertovali, parchanti.. No budiž, aj tak si myslím, že máte celú kozmológiu postavenú doslova na hlavu, lebo teória, ktorá súčasne používa tenzor krivosti IMO odvodený z rotačnej matice reálneho priestoru súčasne s Minkowského rotačnou maticou, musí byť ako celok samosporná. A Einstein to IMO celú dobu pred smrťou vedel, preto vyplazoval ten jazyk, ale nič nepovedal kvôli studenej vojne. Pokiaľ tú vizualizáciu niekto vytvoril ešte za jeho života, tak na to prišiel určite, pretože si to podľa mňa predstavoval presne naopak, v jeho knižkách som teda ten obrázok rozhodne nikde nenašiel. A všetko samozrejme popieram, ako Galileo. A i tak to máte celé naopak. A už som zas ticho..
Re: Re: Inspirativní článek
Petr Zima,2023-04-03 03:11:40
Určitě nebylo mým cílem Vás „dostat“. Vytyčený směr myšlenek je naprosto rozumný. Třeba ty úvahy o tečně jsou obzvlášť pěkné. Váš pokus o netradiční a kontroverzní výklad je nakonec docela přiléhavý a poskytuje vhled, že analýza je trochu o něčem jiném než o sadě výpočetních vzorečků.
Já chtěl jen ukázat, že i takovými věcmi se matematika může zcela korektně zabývat. A také že zabývá, nepodceňujte matematiku. Dokud se nedopouštíte vyložených logických lapsů, tak jen málokterá myšlenka je natolik šílená, aby ji nešlo nějak formalizovat a matematicky zpracovat :-)
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce