S Pythagorou je to těžké. Život a odkaz muže božího, který levituje a bilokuje, je náročné vtěsnat do nějaké rozumné terminologie. S jistotou víme, že opravdu žil, dokonce kde působil a přibližně kdy, a že byl významnou postavou. Pokusil se zásadně zreformovat náboženství, význam má i pro filosofii, ale těžiště jeho dědictví je v matematice a v aplikaci matematiky v přírodovědě. Ostatní je věcí výkladu až dohadů. Zkusíme to nějak postupně rozmotávat a vyvarovat se nekritického přijímání legend. (Pomineme i bratrovražedné boje mezi znalci pravopisu o délku nad ypsilon v českém přepisu jeho jména.)
Život
Pythagorás pocházel buď z ostrova Samu, nebo (snad spíše) z tyrhénského ostrova Lémnu v severovýchodní Egeidě. Narodil se někdy kolem roku 570 před n. l., podle krajních optimistů o 10 let dříve. Na Samu dokonce najdeme městečko Pythagoreion, jenže takto bylo pojmenováno až roku 1955, z důvodů spíše vlasteneckých a turistických, předtím se jmenovalo Dugana. Jeho staré řecké jméno neznáme, možná rovnou Samos. V antice tady bylo sídlo tyrana Polykrata (vládl asi 540 až 522 před n. l.). Dnes tu má Pythagorás velký novodobý památník, jak nedaleko přístavu se školním trojúhelníkem v ruce ukazuje na sklon čehosi nebeského, před vlajkami pravoslaví, EU a Řecka. A v horách Samu se v naší době ukazuje i Pythagorova jeskyně, leč to je asi jen obvyklý následný folklor vázáný na pověsti o mužích božích, v tomto případě nejspíš až novodobý folklor.
|
Památník Pythagory, pozdní 20. století. Pythagoreion na Samu. Kredit: Njaker, Wikimedia Commons. Licence CC 3.0.
|
Vchod do tzv. Pythagorovy jeskyně v pohoří Kerkis na Samos. Kredit: Tomisti, Wikimedia Commons. Licence CC 4.0.
|
Pomineme teď, že svůj bezprostředně předchozí život prožil pod jménem Euforbos na kykladském posvátném ostrově Délu, prý to sám říkal. Problém je v tom, že s jistotou nevíme ani to, jestli to opravdu říkal. Proto přeskočíme detaily tohoto jeho minulého života, i když by vydaly na důkladný článek. Zrovna tak nemá mnoho smyslu probírat jeho životopis od novoplatonika Porfyria, je to spíše hagiografie (světecká legenda), psaná z odstupu osmi staletí, bez návaznosti na starší prameny a bez elementární kritičnosti. Nebýt pozdějších pythagorejců a několika Aristoxenových poznámek z pozdního 4. století před n. l., mohli bychom si povzdechnout s Krhútskou kronikou Ervína Hrycha: „Jediným solidním pramenem je tu výmysl, případně analogie vývoje.“
Do zvláštního stylu náboženství – a podle některých i do filosofie – prý Pythagoru uvedl jiný „muž boží“, totiž Ferekýdés, viz článek Ferekýdés ze Syru – muž boží, mytograf, prý učitel Pythagorův.

V dospělém věku se Pythagorás odstěhoval do jižní Itálie, do řeckého města Krotónu (dnes Crotone) v Kalábrii, v Tarentském zálivu. Tam konal četné zázraky a někdy kolem roku 530 před n. l. založil velice zvláštní školu, která měla ambice reformovat všechny aspekty života, a to prostředky pečlivě cílené pastorace. Získala vliv i v městské radě, proti čemuž se ovšem měšťané tvrdě postavili, pythagorejce vyhnali a zavedli demokracii, snad krátce po roce 510 před n. l. Pythagorejci to líčí jako vyvraždění od nenapravitelných nerozumných chlípníků, jejich odpůrci zase tak, že ať byli krotónští, jací byli, přece jenom měli dost rozumu, aby nepřešli na totalitní teokracii, ještě k tomu podivnou. Pythagorás se uchýlil mezi své věrné v nedalekém městě Metapontion, kde také někdy mezi léty 509 a 495 před n. l. zemřel. V Metapontiu byla jeho památka ctěna, jeho dům byl zasvěcen chrámu a hrobku ukazovali ještě v římské době.
Je to samý paradox. Divotvorný muž boží je důležitou postavou dějin vědy i dějin filosofie. Navíc byl Pythagorás původem Řek z Východu (Ión), leč stal se zakladatelskou postavou typicky západního stylu náboženských reforem a také typicky západního (v řeckém smyslu slova) stylu filosofie, přírodovědy a náboženství.
Ve standardním referátu by po životopisu měl následovat přehled díla. Nezachoval se však žádný fragment nějakého Pythagorova spisu a dnes převažuje mínění, že nepsal. Už v antice to tvrdil např. Diogenés Laertios (VII,7): „To, co se uvádí jako Pythagorovo dílo, pochází od Lýsida, pythagorejce z Tarentu.“ Skalní stoupenci Pythagory ovšem tvrdí, že psal, ale že spisy byly tajné, jen pro vnitřní okruh školy. To samozřejmě nelze vyloučit, leč „tajné“ spisy pozdějších pythagorejců alespoň fragmentárně známe. (Převládá mínění, že v antice se nevykecal jen obsah mystérií, např. eleusinských.) Nepíšící mudrc se může posmrtně stát největším filosofem, zvláště když zanechá oddané žáky. Pythagorův kult se projevil i jeho dodatečným přiřazováním mezi Sedm mudrců.
Škola, esoterici a exoterici
Pythagorás založil školu, dokonce ve smyslu instituce se závaznými pravidly. Byla to první taková škola, patrně taky jediná až do doby, než Platón roku 387 před n. l. založil v Athénách svoji školu, Akadémii. Pythagorejská škola ovšem nebyla jen školou v naukovém smyslu a centrem vědecké práce, nýbrž také velice vyhraněnou náboženskou společností, přímo sektou.
Škola by rozdělena na vnitřní (εσωτερικοϛ) a vnější (εξωτερικοϛ) okruh, tedy na esoteriky a exoteriky. V tomto samotném dělení nehledejme více mystiky než v nápisech „esoteriko“ a „exoteriko“ na poštovních schránkách v Řecku, které rozlišují vnitrostátní zásilky a poštu do zahraniční. Podobně tomu se v dnešním Řecku Ministerstvo vnitra nazývá Ministerstvo Esoterních záležitostí (Υπουργείο Εσωτερικών), zatímco Ministerstvo zahraničních věcí se týká Exoterních věcí (Υπουργείο Εξωτερικών). Esoterní okruh pythagorejské školy pěstoval vědu, zatímco exoterní byl spojovacím článkem s okolní společností.
Pythagorejští esoterici se věnovali především matematice a jejím aplikacím v přírodních vědách. Byli to matematici, tedy učedníci. Samo slovo matematika znamená to, čím se zabývají žáci, žák je řecky mathétés. Zde se ovšem žákem myslí takový žák, který časem zastoupí mistra; v oblasti vědy tedy spíše student až vědec. Ti mají chápat, proč ty či ony matematické výroky platí, mají nahlížet matematické vztahy a úměry, zvláště vztahy geometrické. Exoterici se spokojovali s pasivním přijímáním nauk, byli to pouzí posluchači, řecky akúsmatici. Kritériem pro ně bylo, že „on sám to řekl“, tedy že to pravil Pythagorás. V praxi stačilo, že daný výrok byl Pythagorovi tradicí připsán. Posluchač argumentuje tím, že to říká pan učitel; zatímco esoterik matematickému popisu rozumí, ví, proč platí.
K programu školy určitě patřila taky témata náboženská a filosofická, nejspíš i politická, ale to zatím odročíme. Situaci komplikuje, že zvláště „akúsmata“, tedy „zaslechnuté výroky“, jsou mnohdy velice bizarní, a časem zavdaly podnět k záměně podivností za cosi „esoterního“.
Číslo a matematizace vědění

Vzhledem k absenci spisů z prvních generací školy nám nezbývá než předpokládat jakousi zárodečnou podobu toho, co můžeme číst ve fragmentech spisů pythagorejců 5. a 4. století před n. l., tedy se zpožděním tří až pěti generací. Jinak bychom museli hledat nějaký převrat uvnitř rané pythagorejské školy, pro což nemáme žádné indicie.
Zvláště příznačné je dílo pythagorejce Filoláa z Krotónu (a Tarentu, asi 470 až 400 před n. l.), které se soustředí na matematický popis akustické harmonie, včetně technických otázek hry na strunný nástroj, viz článek Byl Filoláos větší číslo než Pythagorás?, kde jsou i odkazy na literaturu. Technické a zčásti i politické aspekty pythagorejství řecké klasické doby jsem popsal v článku Ing. Archytás Krotónský (i když je spíše Tarentský). Krom toho bývá k pythagorejcům řazen také raně klasický lékař a filosof Alkmaión z Krotónu, viz článek Jak člověk k adjektivu „moudrý“ přišel.
Dnes je celkem široká shoda, že pythagorejští esoterici se (krom jiného) zabývali matematikou a jejími aplikacemi v přírodních vědách a v technice. Toto směřování patrně započal už sám Pythagorás. Nejvýznamnějším objevem je, že matematika může být jak samostatnou vědou, tak nástrojem dalšího poznání. Matematické objekty, čísla a vztahy mezi geometrickými útvary, můžeme zkoumat; s jejich pomocí však můžeme zkoumat i řadu jiných věcí na světě, od astronomických jevů přes hudbu po technické problémy. Máme hledat „čisté úměry“. Úspěch v oblasti akustické harmonie sváděl k iluzi, že na základě jednoduchých harmonií můžeme vyložit úplně všechno, což se projevilo v pythagorejské astronomii. Ta je sice novátorská svým tíhnutím k heliocentrismu (a od klasické doby i skutečným heliocentrismem), ale přezírá měřená data. Není náhoda, že ještě Kepler ve svém Kosmografickém mysteriu postupoval podobně, až výtky pozorovatele Tychona ho přivedly k méně geometricky tradiční formulaci slavných tří zákonů. Ty jsou opět matematické povahy a mají i geometrickou názornost, ale jinou než pythagorejská tradice.
Čísla a geometrické útvary mohou být předmětem vědy (matematiky) i nástrojem dalších věd, přírodních a technických. To je odkaz pythagorejských esoteriků.
Čísla se samozřejmě používala odedávna, ponejvíce na trhu a při výpočtu daní. Prostě kupecké počty. Podobně se odedávna používaly jednoduché geometrické poznatky, třeba k vytyčení pravého úhlu na stavebním place nebo na poli, to kvůli ploše pro daně. Novinkou pythagorejců je teoretický popis, který dává vhled do toho, proč a jak to funguje, a který umožní také nové aplikace.
Nevíme, jestli objevili větu, kterou dnes nazýváme Pythagorova; spíš se zdá, že Pythagorovou novinkou mohla být věta dnes zvaná Thalétova. Kolem pythagorejské matematiky bylo od dob antiky po dnešek vyprodukováno mnoho ideologických výkladů, které nadbytečně přehánějí unikátnost řecké matematiky. Analogické poznatky i praxe jejich aplikací se najde leckde, například ve staré Číně, v Mezopotámii dokonce už ve střední době bronzové (viz link na obrázek).
Přesto byli pythagorejci nejspíš první, kdo upřednostnili formální jazyk pro obecný popis světa. Nejlépe lze skutečnost popsat matematicky! Představovali si to tak, že vztahy mezi čísly jsou přímo principem uspořádání kosmu, a že vztahy geometrické jsou názornějším obrazem vztahů mezi čísly. Proto je tolik překvapilo, že uvnitř samotné matematiky našli problémy se souměřitelností (např. úhlopříčka čtverce, tedy objev iracionálních čísel), podobně jako zbytkové „koma“ při ladění kvintovým kruhem. Pythagorejci by všechny nepřesnosti rádi viděli jen ve smyslové empirii. Číslo pro ně bylo určujícím a vymezujícím principem ve světě, na straně nás lidí číslu odpovídá myšlení; zatímco naše emoční prožívání je podle nich ekvivalentem čehosi neurčitého, nevymezeného, co je v kosmu čísly pořádáno, a mělo by být pořádáno i v našem životě.
Názornost, názor a názory
Není nad to, než když se téma představí názorně. To říkal i Jan Ámos z Komně (Comenius). Názorně, tedy tak, že rovnou vidíme řešení problému, jako když správně nakloníme skládačku hlavolamu. Tehdy je to jasné, vidíme řešení, sami je vidíme, nemusí nám je nikdo říkat. Drobný problém ovšem je, když „matematický názor“ chceme ve škole už po dětech, dokonce jako výchovnou a obecně vzdělávací průpravu. To je spíše osvícenecká myšlenka. Větší problém je, když kýženou názornost zaměníme za nadiktovaný názor, který prý vysvětlí všechno. Podobně, když místo debaty o řešení problému – nebo místo debaty o kompromisu mezi různými zájmy – nastoupí střet názorů. Pythagorejci (a stejně tak Platón) by tomu, čemu my říkáme „názory“, řekli „mínění“ nebo domněnky, a divili by se, jak moc se jimi zabýváme, a proč to vlastně děláme. Střet různých mínění je podle Platóna příležitostí k dialogu, střet zájmů je praktický problém, ale střet názorů, to nedává smysl. (Viz článek Mélský dialog.)
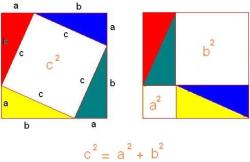
Názorné rozkreslení „Pythagorovy“ věty. Kredit: Anythingyouwant, Wikimedia Commons. Licence CC 3.0.
|
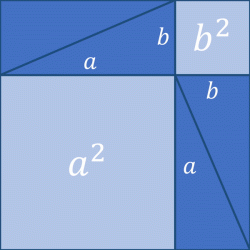
Pohyblivé rozkreslení „Pythagorovy“ věty. Kredit: Julen Artano, Wikimedia Commons. Licence CC 4.0.
|
Pro příklad názornosti teď použijeme Pythagorovu větu, nezávisle na tom, kdo a kdy ji objevil. Formulace s mocninami je algebraická, tedy v naší kultuře až od začátku 2. tisíciletí. Stejně si pod těmi mocninami představíme čtverce, to je síla tradice. Tradiční formulace říká, že plocha čtverce nad přeponou pravoúhlého trojúhelníka je rovna součtu ploch čtverců nad jeho odvěsnami. To se posluchači mohou naučit. Matematik to sám vidí, například na vhodném geometrickém rozkreslení. (Tedy tradiční matematik, nejnovější doba je posedlá formalistním dokazováním.) Taková názornost vede (stejně jako formální důkaz) k jednoznačnému popisu, alternativy jsou možné pouze formulační. Skutečnými alternativami jsou rozličná zobecnění, která ovšem tradiční formulaci obsahují jako jednoduchý případ. Zcela obecně vzato (nezávisle na tomto příkladu) budou alternativami až různé ne-eukleidovské geometrie. To by mohl být také příklad rozumného postupu při diskuzích o alternativách řešení toho či onoho i mimo geometrii. Rozlišovat, kdy opravujeme věcnou chybu, kdy navrhujeme obecnější popis, otevírající novou oblast řešení, a kdy jenom zbytečně trucujeme.
Rub a dluhy
Článek se věnoval hlavně matematizaci poznávání světa, takže zbývá řada otázek. Jak s tím souvisí reinkarnace, zázraky, léčitelství a pozdější esoterismus? A co pythagorejská filosofie? To je na jiná vyprávění, včetně detailů matematických problémů, avšak už teď je na místě alespoň předběžný náčrt.
Pythagorejci jsou detailisté, přesto se však mnozí z nich nerozpakovali falšovat texty reálných i mytických autorů, jindy zase hlásat takovou či onakou životosprávu a vnucovat ji ostatním. Sebevědomí jim opravdu nechybělo. A nezastavili se ani před pokusem přivlastnit si nejen objev matematizace poznání, který jim patří, ale přímo monopol na matematiku jako vědní obor! A nejen na matematiku, ale i na řadu dalších věd, také na filosofii. Dokonce se pokusili vynutit monopol na správné nové náboženství, totiž to jejich.
Zdaleka ne každý řecký matematik byl pythagorejec. Pythagorejci toho sice objevili dost, ale snažili se přivlastnit si všechno. Novou dobu slávy zažili v helénistické a zvláště v římské době, když do Řecka přišla z Východu vlna numerologie. Číslo bylo najednou klíčem k čemukoli, ovšem způsobem zdaleka ne matematickým. Pythagorejci reinterpretovali svoji tradici v duchu dobové módy, jako kdyby i s tou numerologií přišli oni. Nějaké drobné zárodky podobného myšlení u nich asi fungovaly už dřív, např. symbolická role jedničky, dvojky, sedmičky a desítky, ale s pořádnou numerologií přišli až v římské době. Svůj nový výklad matematiky, který začlenil numerologii, pojmenovali „pythagorejská matematika“, jako kdyby byl starý, k tomu si přivlastnili objevy ostatních matematiků, na což jim méně kritická část autorů dějin matematiky naletěla. Nutno přiznat, že tato „pythagorejská matematika“ má notně pošramocenou pověst, ideologizovala se už v průběhu antiky. Příkladem mohou být spisy Theóna ze Smyrny z 2. století n. l. Neprospěla jí ani falza, která měla doložit, že pythagorejci objevili prakticky všechno.
Podobně tomu je ve filosofii. Její založení nebo aspoň pojmenování se v řadě učebnic přisuzuje přímo Pythagorovi, přestože dávno panuje všeobecná shoda o tom, že se takový výklad opírá o pozdější falza textů. Přesto nelze vyloučit, že slovo filosofie mohli používat někteří pythagorejci v době krátce před Platónem, ale o tom jindy. Mimořádná úspěšnost public relations pythagorejců je vidět i na tom, že ještě v tradičním kompendiu textů filosofů z dob před Sókratem v edici Diles-Kranz, mainstreamové v 1. polovině 20. století, je z celkem 90 položek „předsokratiků“ více než 40 pythagorejců! Přitom od většiny z nich nemáme vůbec žádný text a někteří vůbec neexistovali, jejich jména jsou založena pouze dodatečnou etymologickou fabulací některých novoplatoniků, zvláště Porfyria a Jamblicha v 3. století n. l.
Zbývá někdy pojednat také pythagorejské reinkarnace, zázraky a zvěsti akúsmatiků, zvláště o životosprávě. Nemáme sice ostrý doklad, leč vše se shoduje s představou, že už Pythagorás vystupoval velice sebevědomě až pompézně, obřadně a s promyšleným důrazem na misijní aspekt. To k mužům božím často patří. Bylo by však omylem si myslet, že to obecně patří ke staré době. Například Míléťané nebo Hérakleitos nic takového neprováděli. Pythagorás a jeho stoupenci působili v řecké kultuře málem cizí jako těleso, ne vždy trpěné a často zesměšňované, podobně jako orfici a další „očistná hnutí“. (Viz článek Kapka cizí krve v řeckých žilách?.) Obecně vzato nebyli Řekové reinkarnacím nakloněni o mnoho více než omezování v sortimentu jídla a sexu, tedy skoro vůbec. Přesto pythagorejci zásadně ovlivnili řadu dalších filosofů i mimo svou školu, například Empedokla a Platóna. Naopak Xenofanés, Hérakleitos a později skeptici Pythagoru tvrdě kritizovali.
Literatura
Z. Kratochvíl: Filosofie mezi mýtem a vědou. Od Homéra po Descarta. Praha: Academia 2009, s. 62-70.
Antická svědectví o Pythagorovi na mém starém webu www.fysis.cz.
Pythagorejci archaické doby na mém starém webu www.fysis.cz.
Antické legendy a drby o pythagorejcích na mém starém webu www.fysis.cz.
Diskuze:
Pythagorova věta
Petr Zima,2022-10-02 12:02:19
Splehlivých informací skutečně není mnoho, ale téměř jistě Pythagorovu větu neobjevili Pythagorejci. Znali ji nejspíš už i Mezopotámci a jiné civilizace včetně Řeků ještě před Pythagorou. Jestli Pythagorejcům můžeme něco připisovat, tak to její výslovná formulace a hlavně důkaz. Samozřejmě v nějaké té ryze geometrické podobě, coby "očividná demonstrace". Ale víc toho vlastně není potřeba a i z dnešního pohledu takový důkaz obstojí, pokud se nezahrabame v bezbřehém formalismu. Jisté to není, tím méně je jisté, jestli to byl důkaz hitoricky první a jestli jeho autorem byl Pythagoras nebo někdo z jeho žáků.
Matematika se celkově i v těch nejstarších psaných pramenech objevuje (pro někoho možná překvapivě) už v poměrně rozvinuté podobě. Úplné základy aritmetiky, geometrie a vlastně i algebry spadají do předhistorické doby. Dost možná se matematika vyvíjela souběžně s jazykem i dříve než písmo.
Hlavní přínos Řeků v klasickém období byl počátek logiky, snah matematické poznatky zdůvodňovat bez opory ve zkušenosti. A na tom má Pythagorejsá škola určitě lví podíl. Matematika starších civilizací byla sice už dost rozvinutá - formou slovních úloh se uměly řešit třeba i některé kvadratické rovnice - ale měla téměř bez výjimky dogmatickou a empirickou formu. Po celá staletí se třeba používaly pouze přibližné vzorce a nikdo se asi vůbec netrápil tím, aby rozlišoval přesné "věty" od přibližných postupů.
Re: Pythagorova věta
Zdeněk Kratochvíl,2022-10-02 12:51:38
S prvními dvěma odstavci naprostý souhlas, díky.
S posledním je spojena řadu problémů. Ano, logika se rozvíjí až v klasickém období (po 480 před n. l.), nikoli v archaickém. Je ale velká otázka zda je hlavním přínosem Řeků, z hlediska logiků určitě ano. Problém je však s odlišným pohledem Řeků na vztah logiky a mytematiky.
Formální logiku odkryli Eleaté, počínaje Parmenidem, rozvíjeli ji sofisté a Platón, k relativní dokonalosti ji přivedl Aristotelés (napsal její učebnici), formální alternativu podali stoici. Jenže Platón, Aristotelés i stoici logiku nespojovali s matematikou, dokonce ji (podivně) nadřazovali nad matematiku; každopádně se logika a matematika po celou antiku vyvíjely každá zvlášť, kupodivu, byť někteří matematici samozřejmě používali logické úvahy. Antické rozlišování mezi logikou a matematikou působí na našince divně. Oni logiku většinou odvozovali z přirozeného jazyka, jako formální nadstavbu (další zobecnění) gramatiky a syntaxe.
K příbližným vzorcům. Ano, použivaly se často, hlavně v technických aplikací. Přesto měli nejen pythagorejci, ale i Platón, Aristotelés a skeptici (tedy "napříč názorovým spekterm") naprosto jasné vědomí rozdílu mezi přesným řešením a přibližnou aproximací. Výjimkou jsou někteří sofisté, např. Antifón považoval aproximaci za reálnou, zatímco exaktní řešení za pouhou myšlenku matematiků, to byla spíš provokace vůči většině, nicméně některé jeho aproximace později Archimédés převedl do podoby formální cesty k hledání přesného výrazu (vzorců pro křivé plochy a pro objemy rotačních těles) nebo postupného přibližování k přesné hodnotě (např. pí).
Re: Re: Pythagorova věta
Petr Zima,2022-10-02 13:12:52
Ohledně těch přibližných vzorců jsem to myslel právě tak, že to vědomí rozdílu mezi přesným a přibližným řešením se objevuje až u Řeků. Hlavu si s tím moc nelámali Mezopotámci nebo Egypťané, i když už toho také znali dost.
(Pokud vím, nejsem zas takový odborník na historii matematiky.)
Re: Re: Re: Pythagorova věta
Zdeněk Kratochvíl,2022-10-02 13:44:01
Ano, ten rozdíl se většinou připisuje právě Řekům, dokonce už od archaické doby, počínaje právě pythagorejci. V Egyptě prý opravdu takový rozdíl netraktovali. Otázka ovšem je, jestli se nějaká jeho analogie najde v Mezopotámii nebo v Číně. O tom jsou rozličné názory, sám se v tom mimo Řecko vůbec nevyznám.
Re: Re: Re: Re: Pythagorova věta
Petr Zima,2022-10-02 14:34:32
Já to určitě nechci vnímat nějak černobíle jako ostrý zlom u Řeků. Ty nejstarší dochované texty všude začínají v dogmatickém a empirickém duchu, s důrazem na aplikace, ale s postupným rozvojem a hlavně propojováním a systematizací (matematických) poznatků se začíná vynořovat nějaká metoda. A to se minimálně v některých omezených oblastech matematiky dělo už i v té Mezopotámii, Egyptě, Číně nebo později v Indii.
Ono je to tak často i u moderních objevů, spousta jednotlivých poznatků v latentní nebo jen méně systematizované podobě existovala už o dost dříve. Pak se to najednou "vyloupne" a začne dávat pěkný nový smysl. Stejný pohled možná můžeme použít i na samotnou deduktivní metodu*. U těch Řeků se definitivně vyloupla a snad mohu říct, že si ji dokonce vytyčili jako program dalšího zkoumání. A konkrétně ti Pythagorejci to snad zas až přehnali, začali si malovat svůj dokonalý svět a odtrhli se od reality**.
*) Asi je v tomhle kontextu lepší mluvit o dedutivní metodě než o logice.
**) Ať už to znamená cokoli :-) Ale dnes určitě mezi reálná čísla zahrnujeme i čísla iracionální neboli alogická, se kterými měli Pythagorejci trochu problém.
Re: Re: Re: Re: Re: Pythagorova věta
Zdeněk Kratochvíl,2022-10-02 15:11:34
Ano, asi tak. Díky za amplifikace.
Re: Re: Re: Re: Pythagorova věta
Petr Zima,2022-10-02 14:43:33
Mimochodem takové "celostní" propojení vědy včetně matematiky, filozofie a náboženství bylo typické i ve starověké Indii. Tam se i trochu odchylovali od toho pravidla, že matematika začínala všude od zaměření na aplikace. Dogmatický přístup měli také, ale matematiku od počátků popisovali více mysticky, ve spojení s náboženstvím a dokonce ji psali ve verších.
Zalmoxid
Mikulas Alexík,2022-10-01 16:00:09
Pytagoras -Zalmoxid
Mikulas Alexík,2022-10-01 15:57:55
Pred viac ako rokom som Vás v diskusii požiadal o komentár k Pytagorovmu sluhovi(?), či spoločníkovi(?) s menom Astreios (možno je to chybne). Odpísali ste mi v diskusii, kde to nájdem (druhý diel Diogena Laertia). D.L. som doma "vyhrabal" až o 3 mesiace, ale nevedel som to v texte nájsť.
Prosím Vás, môžete mi zopakovať kde sa zmienka o Astreios v D.L. Nachádza?
Ešte 2 otázky.
1. V knižke "Od Zalmoxida po Džingischána" (M. Eliade), som sa dočítal, že žreci u Getov resp. Trákov, pokladajú Zalmoxida za svojho "proroka" (lebo ich presvedčil o metempsychoze. M.E. trocha ironicky komentuje akým "trikom" to dosiahol). Pokladali pritom Zalmoxida za "Pytagorovho otroka", ktorý unikol skaze v Metaponte. Môže byť Atreios a Zalmoxid tá istá osoba?
2. V jednom dlhšom komentári o zlatom reze a Timao (Platón), som čítal ako Descartes pri "starostlivom čítaní Timaa" mal dve "videnia", ktoré ho inšpirovali pri formulácii Analytickej geometrie. (Nebol sám, ktorého čítanie Timaa "inšpirovalo", viď napr. Kepler). Mohlo to byť tým, že pochopil,, kedy je "grécke písmeno iba symbolom pre číslo resp. "premennú" vyjadrenú písmenom (to už je moderný Descsartov vynález). Zdá sa mi, že slovne boli kvadratické rovnice a analytická geometria formulované (viac menej skryto) už v Timao. Dá sa nájsť matematický výklad k Timao v Češtine alebo Slovenčine, prípadne v Angličtine?
Re: Zalmoxid
Zdeněk Kratochvíl,2022-10-01 19:01:16
Toho Astreia teď nenajdu, je to na delší lokte, protože je to hodně okrajová záležitost, a mám teď zrovna na krku začátek semestru. O mnoho ale nepřicházíte, je to opravdu jedna z mnoha pozdních a okrajových verzí, v reálu nikdo takový skoro jistě nežil.
Je dobré si uvědomit, že Pythagorás je sice postavou řady nehistorických fantazijních legend, ale on sám byl reálnou postavou, i když o něm víme strašně málo. Oproti tomu o Zalmoxidovi ani nevíme, jestli je to jméno osobní nebo typologické. Jsou to jen střípky tráckáých mýtů, zaznamenané v řecké literatuře. Eliade je obecně nakloněn hrocené mystice, takže když se i on uchýolí k ironii, tak to něco znamená. Spojitost s Pythagorou (jeho otrok) je dodatečný výmysl, jak od Pythagory odvodit všechno. Prostě Pythagoras je postava historická, zamlžená legendami a pak výmysly, Zalmoxis postava mytická (navíc trácká), Astreios postava, která se mihne v okrajové fantazii.
Archytás pracoval se souřadnicemi, kterým dnes říkáme karteziánské, ale analytickou geometrii v nich zavedl až Descartes. Ona totiž předpokládá algebraické myšlení. To přišlo do Evropy ža kolem roku 1000 n. l. Přesto pythagorejci Platónovy doby, ale i jiní řečtí matematici, chybějící algebru umně obcházeli a řešili řadu úloh, které se později řeší algebraicky.
Řecká písmena mají roli cifer, ne algebraických znaků pro proměnou. Je to dekadický částečně poziční systém zápisu čísel, mnohem přívětivější než římské cifry, jenže taky nemá nulu, což mu chybí k tomu, aby to byl pořádně poziční ciferný systém. Maličký krok směrem k algebře byl občas činěn pojmenováním eličiny, kterou bychom dnes nazvali proměnná. Doporučuju knohu Zbyňka Šíra, Řecké matematické texty; Praha: Oikúmené 2011.
Re: Zalmoxid
Zdeněk Kratochvíl,2022-10-01 19:14:05
Všechno, co o Pythagorovi víme, včetně pravděpodobných domněnek, jsem napsal v tom článku. Pokud si chcete přečíst o 8 století pozdější legendu (včetné minulých životů),najdete ji u Diogena Laertia na prvních stránkách osmé knihy (kapitoly). O nějaké to další století později k téhle legendě přibudou další verze a z jedné z nich vytrhávají novodobí záhadologové toho Astreia.
Re: Re: Zalmoxid
Zdeněk Kratochvíl,2022-10-02 11:00:35
Omlouvám se za tón předchozí odpovědi, psal jsem ji v rychlosti a vypadá, jako kdybych si nárokoval patent na rozum. Věcně je ale v pořádku. Chci rozlišovat, co opravdu víme, a co můžeme představit spíše jako pozoruhodné fantazie, které se v průběhu staletí kolem Pythagora navršily. Časem chystám článek o zvěstech akúsmatiků a o legendách, a tam možná dojde i na toho Astreia, jako na jednu z řady druhotných bizarností.
Trojúhelník 3,4,5
Florian Stanislav,2022-09-29 21:23:47
Velký Pythagoraický pravoúhlý trojúhelník z prken ( latí), jinak zednický víngl, využil každý, kdo stavěl dům nebo třeba jen pergolu nebo vyměřoval záhon.
Když hledám na internetu základní poznatek, pravoúhlý trojúhelník s odvěsnami 3, 4 a přeponou 5 délkových jednotek, tak jsem překvapen.
Třeba
https://www.matweb.cz/pictures/pythagorova_veta.png
nemá plochu c2 vyznačenou jednoduše 25 celými čtverečky ( 5 jednotkových čtverečků by mělo ležet přímo na přeponě a dalších 20 ve 4 řadách nad nimi).
zadal jsem heslo pro Google/ obrázky
Pythagorova věta pravoúhlý trojúhelník 3,4,5
Vylezl jediný rozumný obrázek na
https://skolaposkole.cz/matematika-zs/8-rocnik/pythagorova-veta
https://skolaposkole.cz/storage/app/media/pythagorova.jpg
Čtvercová schémata Pythagorovy věty zde v článku o Pythagorovi jsou hezká. Ale nechtěl bych být školákem, který z toho má Pythagorovu větu pochopit a umět využít.
Animovaný .gif obrázek na
https://cs.wikipedia.org/wiki/Pythagorejsk%C3%A1_trojice
https://upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Pythagorean_theorem_-_Ani.gif/440px-Pythagorean_theorem_-_Ani.gif
je taky hezký, ale rychle zmizí, určitě lepší by byl jen konečný obrázek, kde jsou plochy dobře znázorněné.
Klasický odkaz Wikipedie také nemá jednoduché jednotkové čtverce nad 3,4,5 pravoúhlým trojúhelníkem.
Je hezké, že jsem se dozvěděl, že čtverce můžeme nahradit pravidelnými pětiúhelníky ( pravidelnými n-úhelníky). A kde to použiji.
Re: Trojúhelník 3,4,5
Zdeněk Kratochvíl,2022-09-29 22:31:06
Zdravím! Opravdu není nad poměr 3 : 4 : 5. Možná by Vás potěšil obrázek čtverečků tady:
https://commons.wikimedia.org/wiki/File:Bewijs_stelling_van_Pythagoras.jpg
(Obecně pro hledání obrázků doporučuju téma napřed zadat na české Wikipedii a na ní ťuknout na link vedoucí na Wikimedia Commons. Buď rovnou, nebo přes anglickou verzi Wikipedie.)
Jinak, ta pythagorejská témata nebyla určená pro děti, rozhodně ne pro mladší děti, ty byli prostě v roli akusmatiků. Bylo to pro začínající matematiky, byť třeba hodně mladé.
Ty obecnější útvary souvisí s možností dalších zobecnění věty, což je matematicky zajímavé, uplatnění ale taky nevím. Každopádně však pak má uplatnění ta obecnější matematika, která se tím otvírá. To ovšem mám jen z druhé ruky od přátel, sám jsem v takové složitější matematice pouhý akúsmatik.
Re: Re: Trojúhelník 3,4,5
Florian Stanislav,2022-09-29 22:53:12
Ano. Dohledat se rozumné věci dají, ale pro školní děti by měla být rozumná Pythagorova věta na první ránu, což říkám, že není.
Velmi nerad vytahuji staré věci, ale diskuze u Galilea je uzavřena. Trochu to s Pythagorovou větou přeci jen souvisí.
Chtěl jsem doplnit
Za půl roku oběhne Jupiter 1/10 své dráhy, tedy bude 36° nad obzorem při západu Slunce, Za 1 hodinu Slunce oběhne oblouk 15° ( 360/24 =15), tedy 36 ° je víc než 2 hodiny po západu Slunce . Píšete rozumně, že Jupiter by měl být vidět a snad i měsíčky dalekohledem. Dobře. Pak Thaletova věta a Jupiter je nad přeponou pravuúhlého trojúhelníku.
Pak ale pravoúhlý trojúhelník s přeponou 300 milionů km ( AU) má delší odvěsnu jen 300 milionů *cos 36 ° = 240 milionů km.
Z toho ihned plyne, že takto změřená rychlost světla nebude 300 000 km/s, ale jen 240 000 km/s, což se slušně blíží tehdy naměřenému 220 000 km/s.
Je otázka, jestli ono ihned je správně, když nevím, jak Rømer uvažoval a měřil. Obrázky a popis se liší na dole uvedených odkazech.
https://e-manuel.cz/wp-content/uploads/2022/03/17_58.png
Zpoždění měsíců je dáno t = s/v. Tedy zpoždění závisí na změně vzdálenosti.
Je-li vzdálenost určena špatně, třeba určena je menší, tak rychlost bude taky menší.
Další zdroj
https://www.hvr.cz/2016/03/29/kdo-prvni-zmeril-rychlost-svetla/
"při vzdálení Země od Jupitera trvá světlu déle, než k Zemi dolétne, a proto dojde ke zpoždění daného úkazu. Ze svých pozorování byl schopen odvodit, že světlu trvá asi 11 minut, než přeletí poloměr oběžné dráhy Země. Tyto výsledky byly publikovány v roce 1676 a Christian Huygens ze svého odhadu vzdálenosti Země od Slunce určil rychlost světla asi na 220 000 km/s.
http://www.hvezdarnaplzen.cz/wp-content/uploads/2016/01/jupiterconjunction1400x1000-500x390.jpg
Tento obrázek souhlasí s mými výpočty měření za půl roku a při pohybu Jupitera. Průměr dráhy Země mu tedy vycházel Rømerovi 22 minut.
Můj závěr : Jestliže k poloměru dráhy Země naměřil zpoždění 11 minut, tak je čas evidentně špatně, protože poloměr dráhy Země (1 AU) uletí světlo za 8 minut 20 sekund.
Re: Re: Re: Trojúhelník 3,4,5
Zdeněk Kratochvíl,2022-09-29 23:17:32
To, co píšete, dává rozum. Nejsem si ale vůbec jistý správností obsahu citováné věty, že světlo podle starého měření uletí 1 AU za 11 minut. Na odkazovaném webu to opravdu píšou. V textech, které jsem víceméně náhodně potkal a které nedokážu v dohledné době ověřit, byl však údaj 1 a čtvrtina AU za 10 až 11 minut. Při tehdejší technice si umím představit nejistotu do 1 minuty.
Každopádně v 2. polovině 17. století dokázali dobře spočítat okamžitou vzdálenost Jupitera od Země v kterémkoli okamžiku (v jednotkách AU), dokonce se zohledněním elips, - ale podceňovali délku AU, otázka je, o kolik, a zda to nestačí k vysvětlení chyby v měření rychlosti světla. Zeptám se dvou znalejších historiků astronomie a pokud se dozvím něco zajímavého, napíšu o tom "ještěk".
Re: Re: Re: Re: Trojúhelník 3,4,5
Florian Stanislav,2022-09-29 23:40:43
Děkuji. Ale 1,25 AU :10,5 min = 0,12 a 1 AU : 8,3 minuty = 0,12. Takže tam by chyba nebyla, rychlost bude stejná 300 000 km/s.
Re: Re: Re: Re: Re: Trojúhelník 3,4,5
Zdeněk Kratochvíl,2022-09-30 11:40:09
Nezdá se mi, že by se Rømer dopustil takového typu chyby, tedy špatného určení rozdílu vzdáleností v astronomických jednotkách. Tipuji, že rychlost světla v AU za minutu měřil s přesností lepší než 5 až 10%. Naopak je shoda, že až do pozdního 18. století byla velikost AU v kilometrech (resp. v dobových pozemských délkových jednotkách) hrubě podceňovaná. Další možností vzniku tak velké chyby by bylo nedorozumění při předání dat mezi Rømerem a Huygensem. Chce to šťourání v pramenech, což není prosté, a teď těsně před začátkem semestru pro mě neschůdné. Tak snad někdy v zimě.
Re: Re: Re: Re: Re: Re: Trojúhelník 3,4,5
Florian Stanislav,2022-09-30 12:21:43
Jsou v tom zmatky.
http://www.hvezdarnaplzen.cz/wp-content/uploads/2016/01/jupiterconjunction1400x1000.jpg
Čas Roemera je určen patrně špatně kvůli stínu a polostínu za Jupiterem.
Obrázek hvězdárny Plzeň je dobrý, ale stín musí směřovat od Slunce (ne od Země, jak je na obrázku).
Tam je ale dobře poloha zapadajícího měsíce IO, který je na přímce střed Slunce- okraj Jupitera.
Jiné zdroje uvádí polostín Jupitera k měsíci IO, když je Slunce mezi Zemí a Jupiterem.
Jinak to popisuje hvězdárna Pardubice, kde započítávají i rychlost Země ( 30 km/s je ale hodně málo proti 300 000 km/s)
https://www.astropardubice.cz/1-historicka-technika-mereni-velikosti-rychlosti-svetla-ve-vaku-v-astronomii/
https://www.astropardubice.cz/wp-content/uploads/2017/04/romer-model-300x294.jpg
Re: Trojúhelník 3,4,5
Z Z,2022-09-30 02:19:31
Ako "geometrický dôkaz" Pytagorovej vety je dobrý aj takýto obrázok:
https://commons.wikimedia.org/wiki/File:PythagorasSatz.jpg
https://commons.wikimedia.org/wiki/File:Pythagore_square.png
Plocha štvorca v prostriedku je ((b - a) na druhú).
Trojuholníky okolo sú spolu 2ab.
Celé spolu to je potom (a na druhú) + (b na druhú).
A keďže strana celého štvorca je c, tak je to zároveň aj (c na druhú).
Pripadá mi to najviac geometricky "očividné".
No neviem, či žiaci neberú Pytagorovu vetu skôr ako vzorec (( b - a ) na druhú).
Re: Re: Trojúhelník 3,4,5
Zdeněk Kratochvíl,2022-09-30 11:26:58
Pěkné obrázky, díky. Taky souhlasím, že většina žactva si Pythagorovu větu pamatuje v algebraické formě, protože je nejkratší a tudíž nejschůdnější pro paměť. Velká část z nich si asi ty druhé mocniny současně představuje jako čtverce, vždyť takhle běžně mluvíme o jednotkách plochy (2D), v tom je zbytkový zátisk pythagorejské názornosti. Skutečný vstup do "matematického světa" se asi povede jenom některým, k malé radosti didaktiků matematiky. Ti by chtěli, aby každý člověk byl matematikem. Přitom pro praktické aplikace je to v drtivé většině případů dost jedno, stačí úroveň "posluchačů", kteří znají formuli. Tohle nemám opřené o žádnou studii, proto jsem o tom nepsal v článku. Jen na základě dlouhodobé zkušenosti v rozličných prostředích si myslím, že schopnost "matematického názoru" jen málo souvisí s obecnou inteligencí. Jednou mě partička přátel antikářů a filosofů požádala u výklad základů sférické gometrie, potřebovali to k pochopení starých textů. Kvůli názornosti padly 2 kg rozkrájených pomerančů, ale úspěch se skoro nedostavil. Přitom to byli hodně inteligentní lidé, kteří se zase jindy na mě málem dívají spatra, když špatně určím nějaký zavilý gramatický tvar ve staré řečtině.
Ještě horší je to na středních a vyšších školách s filosofií. Podle mé zkušenosti je to často bohužel předstíračka. Omlouvám se.
Re: Re: Re: Trojúhelník 3,4,5
Z Z,2022-09-30 18:59:02
Poslednú vetu som napísal, že sa dala vyložiť rôzne.
Myslel som to tak, že ak by sa vzorce ((a + b) na druhú) a ((a - b) na druhú) vyučovali neskôr ako Pytagorova veta, tak by nebol taký obrázok pre takých žiakov použiteľný na geometrický dôkaz.
Nepoznám poradie, v akom sa čo vyučuje.
V čase Pytagora bola vraj aritmetika a geometria viac prepojená, násobenie sa zobrazovalo ako obsah obdĺžnika, či zoradenie kamienkov do tvaru obdĺžnika a pod.
Re: Trojúhelník 3,4,5
Petr Zima,2022-10-02 12:36:02
Použítí (podobných) trojúhelníků, pětiúhelníků nebo třeba hvězdiček odkazuje k obecnějšímu faktu, že všechny plochy rostou s druhou mocninou délek. Už i ti staří Řekové (snad i přímo Pythagorejci, ale nejsem si jistý a dohledávat to teď nebudu) kromě "čtvercových čísel" 1, 4, 9, 16, ... zkoumali i "trojúhelníková čísla" 1, 3, 6, 10, ... apod.
Ohledně (dnešním jazykem) spojitých veličin dokonce hlídali o jakou veličinu se jedná a tedy důsledně rozlišovali délky, plochy a objemy. Míchat "hrušky s jabkama" bylo zapovězeno :-) Hodně pracovali také s poměry, ale poměr pro ně byl také samostatný pojem a jiná kvalita. K plnému osamostatnění pojmu (necelého) čísla coby abstraktního pojmu bez vazby na reálnou kvantitu nebo jejich poměr došlo až ve středověku.
Perlička na okraj
Petr Hilaris,2022-09-29 16:41:13
Přisuzování různých myšlenek Pythagorovi je občas lákavé. V Metapontu se ke konci 5. století př.n.l. razily stříbrné mince, které měly na líci i na rubu obilný klas. Obraz na rubu byl přitom věrnou inverzní kopií obrazu na líci. Toho by bylo možné dosáhnout silným vbitím lícového razidla do tenkého střížku (tj. tenkého kotoučku stříbra), protože pak by se lícový obraz přenesl inverzně i na druhou stranu. Nicméně v Metapontu používali lícové i rubové razidlo, přičemž to rubové neslo inverzní lícový obraz a při ražbě musela být poloha a orientace obou razidle pečlivě sladěna, aby obrazy na líci i rubu mince byly přesně proti sobě a iluze negativního otisku na rubu byla dokonalá. Analogický postup používali i v relativně blízkém Sybaris, jen místo klasu měli na mincích býka. Dříve byla populární hypotéza, že podnět k tomuto zvláštními designu mincí dal sám Pythagoras. Tato hypotéza vycházela jednak z datování počátku těchto ražeb zhruba do doby jeho příchodu do Metaponta, jedna z toho, že jeho otec Mnesarchos byl údajně rytec gem. Nicméně novější poznatky kladou začátek produkce těchto zvláštních mincí někam mezi roky 550 až 530, což Pythagorův vliv vylučuje.
Odkaz na ukázku takové mince (snad je dovoleno sem vkládat nekomerční odkazy):
https://www.moneymuseum.com/en/coins?&id=774
Mimochodem, pěkná je kapitola Názornost, názor a názory.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce





