Magnet pro experiment Muon g-2 byl do laboratoře Fermilab převezen ze svého předchozího stanoviště v Brookhavenu. Foto Reidar Hahn, Kredit: Fermilab.

Nově prezentované výsledky velice přesných měření dipólového magnetického momentu mionu by se mohly stát dalším průhledem k nové exotické fyzice za Standardním modelem hmoty a interakcí. Zatím nejpřesnější měření prezentoval ve středu experiment Muon g-2, který pracuje v laboratoři Fermilab ve Spojených státech. Velikost magnetického momentu mionu, stejně jako elektronu, lze měřit s extrémní přesností. Zároveň dokážeme s podobně vysokou přesností spočítat jeho hodnotu s využitím kvantové teorie pole popisující interakce ve Standardním modelu hmoty a interakcí, což je současná teorie popisující strukturu hmoty a její interakce. Pokud se pak nalezne odchylka mezi experimentální a teoretickou hodnotou, jde o projevy signálů nové fyziky, která je za tímto Standardním modelem.

Standardní model hmoty a interakcí

Připomeňme, že Standardní model hmoty a interakcí obsahuje částice hmoty, kterými jsou šestice kvarků (u, d, s, c, b, t) a šestice leptonů (elektron, elektronové neutrino, mion, mionové neutrino, tauon, tauonové neutrino), a také jejich antičástice. Dále obsahuje i interakce, které umožňují vytváření vázaných systémů a přeměnu částic mezi sebou. Ty se v této teorii popisují pomocí kvantových teorií polí prostřednictvím výměny částic ve virtuální podobě. Existují tři interakce. Silná, která působí pouze na kvarky je zprostředkovaná osmicí gluonů ve virtuální podobě. Elektromagnetická, která je zprostředkovaná fotony ve virtuální podobě. Slabá interakce, to je jediná interakce působící na neutrina, je zprostředkována bosony W⁺, W^- a Z ve virtuální podobě. Ve Standardním modelu je ještě jedna částice, kterou je higgsův boson. Ten je spojen s mechanismem, který generuje rozdíl mezi hmotnostmi fotonu a bosonů W a Z. Podrobnější popis částic Standardního modelu i těch hypotetických mimo něj jsou v dřívějším článku.

Kvantově polní popis interakcí je daleko komplikovanější, než je výměna jednotlivých zmíněných virtuálních částic. Může se při tom vyměňovat více virtuálních částic. A dokonce přispívají k interakcím komplexní výměny, kde figurují i virtuální podoby částic hmoty. Při interakci se tak vytvářejí a zanikají virtuální páry leptonu a antileptonu nebo kvarku a antikvarku.

Příspěvky jsou tím menší, čím je větší a komplexnější systém vznikajících a zanikajících virtuálních částic. Jednotlivé z nich můžeme popsat pomocí tzv. Feynmanových diagramů, kde jsou virtuální částice zobrazeny různým typem linie nebo vlnovky mezi pevnými vrcholy grafů. Reálné částice mají jeden konec volný, je buď na začátku nebo konci grafu. U virtuálních je to složitější, ale většinou končí oba jejich konce ve vrcholech. Velikost příspěvku daného grafu je dána počtem jeho vrcholů. Čím více vrcholů je, tím je příspěvek grafu menší.

Virtuální částice, jejichž „doba existence“ je omezena Heisenbergovým principem neurčitosti, mohu mít klidovou energii (hmotnost) vyšší i řádově, než je energie v systému dostupná. Na této úrovni tak nemusí být splněn zákon zachování energie nebo se na to lze dívat i tak, že virtuální částice nemusí mít odpovídající klidovou energii. Ovšem, čím je klidová energie dané virtuální částice větší, tím je příspěvek daného diagramu k interakci menší. Vakuum, ve kterém se pohybují reálné částice tak není prázdné, ale je vyplněno neustále vznikajícími a zanikajícími virtuálními částicemi. Podrobnější rozbor komplexního popisu vakua pomocí kvantové teorie pole je ve starším článku.

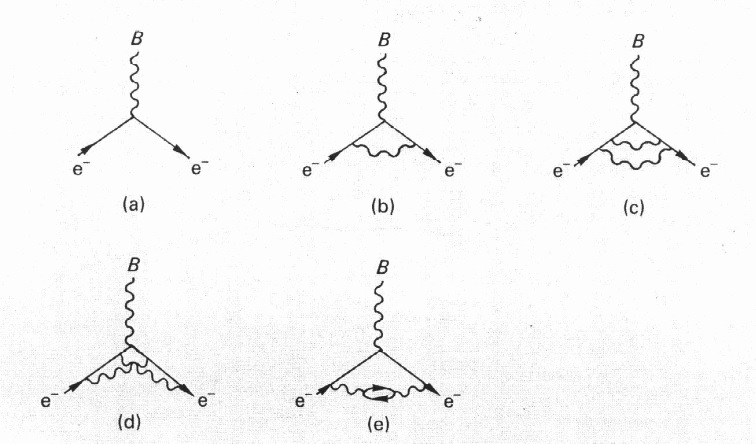
Feynmanovy diagramy popisující příspěvky k magnetickému dipólovému momentu elektronu z kvantové elektrodynamiky. Graf (a) ukazuje příspěvek nejnižšího řádu. Další pak ukazuje vyšší řády.

Magnetické dipólové momenty částic

Některé částice ve Standardním modelu mají magnetický dipólový moment, jsou magnetkami, které vytvářejí magnetické pole. Pokud jsou dané částice bodové, měl by být jejich dipólový magnetický moment dominantně dán jejím spinem (vnitřním momentem hybnosti), u něj je závislost lineární. Stejně tak je lineárně závislý na elektrickém náboji částice. Naopak na hmotnosti je závislý nepřímo úměrně. Elektron, mion i proton mají stejný spin i elektrický náboj. Naopak jejich hmotnosti se dramaticky liší. Takže magnetický dipólový moment elektronu je největší, protože jeho hmotnost je nejmenší. Hmotnosti mionu je téměř dvěstěkrát větší, jeho magnetický moment je tak skoro dvěstěkrát menší. Proton je skoro dvou tisíckrát těžší, než je elektron, jeho magnetický moment je tak zhruba stejnou měrou menší.

Připomeňme ještě, že proton není bodovou částicí, má složitou strukturu dominovanou třemi kvarky. Proto se jeho magnetický moment liší od předpovědi pro bodový náboj výrazněji. To že má proton odlišný, tedy anomální, magnetický moment, se vědělo ještě před tím, než se zjistilo jeho kvarkové složení. A právě anomální magnetický moment protonu byl již v těchto dřevních dobách signálem o jeho komplikované struktuře. Neutrální bodová částice nemůže mít magnetický moment. Anomální nenulový magnetický moment neutronu tak byl známkou jeho komplikované struktury složené z elektricky nabitých elementárnějších částic, dnes víme, že jsou to kvarky. Je to podobné tomu, co známe z klasického světa. Objekt může být celkově neutrální, ale uvnitř se může skládat z nabitých částí. Pokud pak rotuje, má moment hybnosti, náboje se pohybují a generují magnetické pole. Dostaneme magnetku.

I u bodových částic se objevují odchylky od jednoduché předpovědi. V tomto případě jsou však „anomálie“ velmi malými korekcemi danými interakcemi s kvantovými polí popisujícími vakuum v okolí částic. Ty jsou dány popsanými vlastnostmi vakua (polí) v okolí částice a jsou popsaný zmiňovanými Feynmanovými diagramy se stále větším počtem vrcholů a počtem virtuálních částic, které v okolním vakuu stále vznikají a zanikají. Pokud chceme pomocí kvantově polních teorií Standardního modelu spočítat velikost této opravy, musíme zahrnout všechny možné Feynmanovy diagramy se stále větší úrovní komplexnosti a stále větším počtem vrcholů. Příspěvky můžeme rozdělit na tří části. První příspěvky jsou dány kvantovou elektrodynamikou a vystupují v nich virtuální leptony a fotony, druhé jsou způsobeny elektroslabou interakcí a vystupují tam W a Z bosony i higgsy. Třetí příspěvky jsou spojeny s kvantovou chromodynamikou (silnou interakcí) a jde o diagramy, kde jsou virtuální kvarky a gluony (hovoříme hadronové polarizaci). Příspěvky prvního a druhého typu se dají počítat ze základních principů teorie a velice přesně. Přesnost je zde omezena jen matematickou náročností a velikostí potřebného počítačového výkonu. U třetího typu je situace složitější, tam potřenou teorii neznáme na potřebné úrovni a jejich výpočet je komplikovanější a jeho přesnost je závislá na přesnosti experimentálních dat silně interagujících částic.

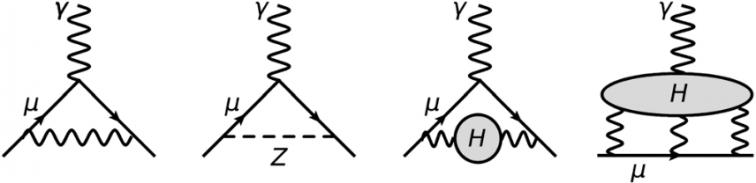
Ukázka Feynmanových diagramů příspěvků vakua zleva, příspěvek z kvantové elektrodynamiky, příspěvek z elektroslabé interakce, a nakonec dva příspěvky započítávající hadronovou polarizaci určovanou z kvantové chromodynamiky. (Zdroj PRL 126(2021) 141801)

Problém pro srovnání experimentu a teorie tak není jen dosažení co největší přesnosti měření, ale take zajištění co nejpřesnějšího určení teoretické hodnoty. Kvantová elektrodynamika, jejíž vliv dominuje zvláště u lehkého elektronu, umožňuje určit jeho magnetický dipólový moment s extrémní přesností. Jeho hodnotu můžeme rozdělit na součin dvou částí. První je součin tzv. gyromagnetického poměru g a spinu částice, druhým pak magneton dané částice, který je dán podílem jejího náboje a hmotnosti a některých fyzikálních konstant (Planckovy konstanty a rychlosti světla). Druhý člen v podstatě představuje přirozenou jednotku, ve které daný magnetický moment vyjadřujeme.

Pro bodovou částici je gyromagnetický poměr 2. Pokud má spin 1/2, jako je to u elektronu a mionu, je hodnota před jednotkou 1. Jak bylo zmíněno, lze u elektronu opravy na korekce stále vyšších řádů vyplývající z kvantové teorie pole pro gyromagnetický poměr určit s extrémní přesností. Teoreticky stanovené číslo před jednotkou magnetického momentu, která se v případě elektronu označuje jako Bohrův magneton, je tak v současné době:

gˑI = 1,001 159 652 181 64(76)

V závorce je nejistota tohoto určení. Nejpřesněji změřená hodnota je v současné době:

gˑI = 1,001 159 652 180 73(28)

Je vidět, že rozdíl mezi experimentem a teorií se projevuje až na třinácté až čtrnácté platné cifře a je v mezích uvedených experimentálních nejistot.

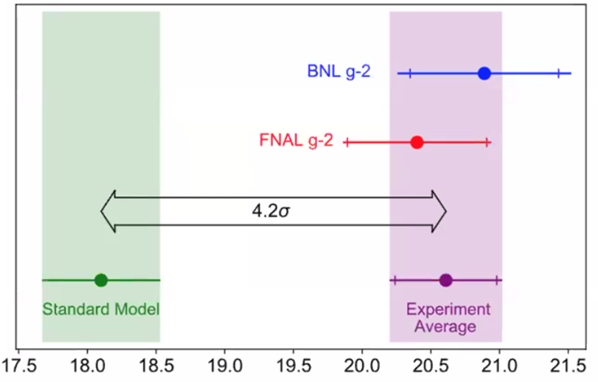
Koncová část současné hodnoty magnetického dipólového momentu mionu vynásobená miliardou. Jde o osmou a devátou cifru za desetinou tečkou. Je vidět odchylka dosahující velikosti čtyř standardních odchylek. (Zdroj PRL 126(2021) 141801)

Magnetický dipólový moment mionu

Mion je skoro dvěstěkrát těžší, než je elektron. Jeho anomální část magnetického momentu je silněji ovlivněna příspěvky, které nepatří do kvantové elektrodynamiky. A je i větší šance, že se zde projeví i vliv nové exotické fyziky za Standardním modelem. Tato nová fyzika může také obsahovat nové částice. Ty sice mohou být mnohem těžší, než jsou ty ze Standardního modelu. Nelze je tak produkovat ani na těch největších urychlovačích, jako je třeba LHC. Ovšem mohou být ve virtuální podobě přítomny ve Feynmanových diagramech, které popisují anomální část magnetického momentu mionů. Projeví se tak ve velikosti odchylky teoretické hodnoty určené jen ze Standardního modelu od té experimentální. Náznaky existence takové odchylky se objevily už na začátku století, ale teprve nyní se začínají díky zvyšování přesnosti měření i teoretického výpočtu dostávat do oblasti s vysokou věrohodností.

Jedním z pracovišť, které se zabývá co nejpřesnějším měřením magnetického dipólového momentu mionu, je experiment Muon g-2 v laboratoři Fermilab v USA. Ten nyní zveřejnil první výsledky měření magnetického momentu mionu. Určená hodnota:

gˑI = 1,001 165 920 40(54)

Ta je ve velmi dobré shodě s předchozím nejpřesnějším experimentálním výsledkem pořízeným Brookhavenské národní laboratoři pomocí experimentu E821. Střední vážená hodnota obou zmíněných měření pak poskytuje zatím nejpřesnější hodnotu určení magnetického momentu mionu a jeho opravy dané kvantovou teorií pole:

gˑI = 1,001 165 920 61(41)

V současnosti uváděná nejpřesnější teoretická hodnota získaná pomocí Standardního modelu je:

gˑI = 1,001 165 918 10(43)

Magnetický shromažďovací prstenec experimentu Muon g-2 . Foto Reidar Hahn, Kredit: Fermilab.

Jak magnetický dipólový moment měřit?

Jak už bylo zmíněno, mion se díky svému magnetickému dipólovému momentu chová jako malá magnetka. Když se dostane do magnetického pole, začne s ním interagovat. Začne vykonávat precesní pohyb, jehož frekvence je dána intenzitou magnetického pole a velikosti magnetického dipólového momentu magnetky. Co nejpřesnějším změřením frekvence, která se u částic označuje jako Larmorova frekvence, pak lze určit velikost magnetického momentu té částice.

Pro co nejpřesnější její určení v případě mionů je potřeba mít magnet s velice homogenním průběhem magnetického pole. Takový magnet je velmi náročný na konstrukci. To je i důvod, proč experiment Muon g-2 využil stejný magnet s poloměrem sedm metrů, který měl předchozí experiment E821. Ten se tak v roce 2013 přestěhoval z Brookhavenu do Fermilabu. V laboratoři Fermilab využívá velice intenzivní zdroj mionů, který poskytují tamní urychlovače. Miony pak mnohonásobně cirkulují v konstantním a velmi homogenním magnetickém poli poskytovaném zmíněným magnetem. Práce na seřízení a co nejpřesnějším nastavení magnetu je velice náročná. To je i důvod, proč jeho příprava trvala zhruba čtyři roky. Po následné roční první etapě měření tak bylo možné prezentovat první popsané výsledky měření. Předpokládá se postupné zvyšování statistiky a další analýzy systematických nejistot, které povedou ke zvýšení přesnosti.

Závěr

Potvrzení výsledků měření magnetického dipólového momentu mionu dosažených experimentem E821 v Brookhavenské laboratoři je velice důležité. Už tato data ukazovala na odchylku od teoretické hodnoty získané pomocí Standardního modelu hmoty a interakcí. Nyní je tato odchylka na úrovni čtyř standardních odchylek, a tedy na poměrně vysoké úrovni pravděpodobnosti. V dalších letech se bude intenzivně pracovat na zvýšení přesnosti experimentální hodnoty i teoretického výpočtu. Ke zpřesnění experimentální hodnoty by mohl přispět experiment E34 v laboratoři J-PARC, který by se mohl rozběhnout v roce 2024.

Zpřesnění určení rozdílu mezi experimentální a teoretickou hodnotu by tak mohlo poskytnout informaci o vlivu hypotetických nových částic, které ve virtuální podobě ovlivňují vlastnosti vakua okolo mionu a tím i magnetický moment. Z tohoto rozdílu by se pak mohly určit vlastnosti, například klidové energie těch částic. Pochopitelně je otevřenou otázkou, co přesně bude možné o nové fyzice za Standardním modelem z daného rozdílu zjistit. S největší pravděpodobností asi nepůjde určit přesně hypotézu a hypotetické částice, které za rozdílem stojí. Spíše půjde o možnost vyřazování těch hypotéz, které mu odporují.

Z toho hlediska začíná být situace zajímavá. Začínají se objevovat i další rozdíly od předpovědí Standardního modelu. Nedávno se podařilo experimentu LHCb pozorovat rozdíl při testování leptonové univerzality v rozpadech B mezonů. Popis experimentu je spolu s dalšími novými výsledky získanými pomoci urychlovače LHC popsán v nedávném článku. Pokud by se například daly tyto odchylky vysvětlit v rámci jedné hypotézy fyziky za Standardním modelem, tak by to mohlo znamenat značný průlom v naší cestě za jeho hranice. Je vidět, že se můžeme těšit v následujících letech na zajímavé fyzikální objevy.

Výsledky byly publikovány v článku v časopise Physical Review Letters a presentovány na semináři 7. dubna 2021.

Starší přednáška věnovaná vlastnostem vakua: