V nedávném článku jsem se pokusil shrnout současné poznatky o epidemii COVID-19 a také, co bylo hlavním důvodem českého selhání při druhé vlně. Pod článkem vznikla velmi dlouhá a zajímavá diskuze. Část diskutujících zpochybňovala testy PCR a hlavně data, která se pomocí nich získala. V reakcích Čeňka Pospíšila, a hlavně v dlouhé diskuzi s panem Daliborem Štysem jsem dospěl k přesvědčení, že nejen oni vykazují základní nepochopení právě pravděpodobnostních a statistických hledisek problematiky okolo testů. Jde o fascinující oblast matematiky, kde se člověk často nevyhne zavádějícímu vlivu prvního pohledu a selského rozumu a setká s fascinujícími paradoxy. Jako většina lidí jsem se i já jimi nechal nejednou nachytat. Podívejme se na ní v souvislosti s jednou oblastí související se současnou koronavirovou epidemií.
Před tím, než se do toho pustíme, dovolím si ještě jednu důležitou poznámku. Jsem fyzik, nejsem virolog, epidemiolog, biolog nebo lékař. Budu se tak v následném textu zabývat dominantně matematickými, pravděpodobnostními a statistickými aspekty daného problému. Tedy, pokud jde o nejistoty různých diskutovaných veličin, půjde o nejistoty statistické. Záležitosti týkající se jiných stránek nechám spíše na kompetentnějších odbornících.
V diskuzi pod zmíněným článkem také někteří tvrdili, že matematika a statistika jsou jiné v biologii a medicíně než ve fyzice, a že se tak k nim nemůžu fundovaně vyjadřovat. S tím ovšem opravdu nemohu souhlasit. Matematika a statistika jsou stejné ve všech oblastech vědy a další činnosti. Je pravdou, že hlavně v medicíně se často setkáváme s omezenou možností provádět opakování měření a získat jejich větší počet. Zároveň je často velký důraz na individualitu daného případu (pacienta), proto je tam často nutné pracovat a pravděpodobnostně analyzovat i jen velmi malé počty případů. Ovšem to neznamená, že bychom se v jiných oblastech, a i ve fyzice, s takovými podmínkami nesetkávali. Jako příklad ze svého oboru bych mohl jmenovat studium produkce supertěžkých prvků. U těch nejtěžších se produkují pouze jednotlivé kusy, někdy pouze jeden či dva. Přesto nám právě využití pravděpodobnostní a statistické analýzy umožňuje získat informace o řadě jejich chemických a fyzikálních vlastností. Jak je důležitá opravdu seriózní statistická analýza a hlavně určení statistických nejistot a relevantnosti, je třeba vidět na diskuzi výskytu leukemie v okolí jaderných elektráren, analýze výskytu rakoviny štítné žlázy v oblastech Japonska zasažených jadernou havárií ve Fukušimě I, posuzování nebezpečnosti amalgamových plomb, při porovnání různých metod a analýze historických dat o oxidu uhličitém v atmosféře získaných s velmi rozdílnou přesností. Analýza statistických a systematických nejistot je nutná u každého měření a hodnota bez znalosti nejistot nemá smysl
Studie Státního zdravotního ústavu a data o relativním počtu pozitivních testů v Německu
Pro vysvětlení problematiky jsem si vybral konkrétní téma, které do diskuze pod zmíněným článkem vnesl pan Dalibor Štys, aby zpochybnil data získaná testováním, a obecně užitečnost a potenciál PCR testů. Nejspíše jde o věc, která koluje a diskutuje se na sociálních sítích dost intenzivně. Bude tak zajímavé je využít pro lepší pochopení dané problematiky
První materiál, na který se pan Dalibor Štys odvolal, byla srovnávací studie Státního zdravotního ústavu, která testovala kvalitu jednotlivých laboratoří. Zaslala jim referenční vzorky, z nichž některé obsahovaly virus SARS-CoV-2, jiné čistou vodu a další chřipkový virus. Kontrolované laboratoře nevěděly, o jaké konkrétní vzorky se jedná. Ze zaslaných protokolů se pak zjišťovalo, zda konkrétní test vzorku dosáhl správného výsledku. Zajímavým údajem je, kolik pozitivních vzorků bylo určeno správně jako pozitivní. A možná ještě zajímavější jsou data o pozitivitě u vzorků vody a chřipky. Tedy, kolik bude falešně pozitivních případů.
Druhým materiálem, ze kterého vycházel pan Dalibor Štys, je přehled o testech, které probíhají v Německu. Zde jsou uváděny celkové počet testů a kolik jich bylo pozitivních pro každý týden. Z těchto hodnot je vidět, že v letních týdnech se počet pozitivních testů dostal k hodnotám i pod jedno procento, nejnižší byl 0,59 %.
Ze závěrů zprávy Státního zdravotního ústavu pan Dalibor Štys vyvozuje, že falešná pozitivita na čistou vodu je 3% a na chřipkový virus 4,4%. To je v rozporu s tím, že hodnoty poměru pozitivních případů jsou při testování v Německu menší než jedno procento. Totéž deklarují i některé série testování málo zasažených populací i u nás, například studie z Ostravska národního koordinátora testování Mariána Hajdúcha. Což ovšem podle pana Štyse odporuje předchozím číslům a hodnoty poměru pozitivních testovaných nemohou dosáhnout tak nízkých hodnot, jako deklarují Němci a Marián Hajdúch. Zároveň chybně upozorňuje, že podle studie Státního zdravotního ústavu je falešná pozitivita u vzorku s chřipkou vyšší než u vzorku s čistou vodou. Pan Štys tak předkládá hypotézu, že přítomnost jiných virů snižuje specificitu testu a zvyšuje falešnou pozitivitu. Dále předpokládá, že u rýmy bude toto zvýšení falešné pozitivity ještě vyšší a že současný nárůst pozitivních případů je dán sezonním vzrůstem rýmových onemocnění na podzim a odpovídajícímu vzrůstu počtu falešných pozitivit.
Podívejme se na to, zda opravdu lze z těchto dat takovou hypotézu vyvodit. Předtím musím ještě přidat důležité informace o zmíněné české studii. V tomto případě šlo o kontrolu kvality různých laboratoří. Při ní se kontroluje praxe laboratoře nejen při testování, ale i při zacházení se vzorky a organizaci a zúřadování měření a nahlášení jeho výsledku. I proto je v takovém případě realizován a posuzován relativně velmi omezený počet testů. Ve zmíněné analýze jich bylo u každého typu vzorku (koronavirus, voda, chřipka) méně než sto. Nejde o typ studie, která by například testovala senzitivitu a specificitu testů, kde musí být počet testů o několik řádů větší. Závěrem studie je tak hodnocení 80 posuzovaných laboratoří. Z nich 76 bylo označeno za úspěšné, z toho 51 mělo 100 % úspěšnost (připomínám, že se nehodnotily pouze výsledky testů, ale další parametry). Za velkou chybu považuje studie nezapsání hodnoty Ct, protože vysoké hodnoty přes 39 mohou vést k falešné pozitivitě výsledku. V tomto duchu se neslo i doporučení komise, aby v případě pozitivního výsledku s hodnotu Ct vyšší než 39 byl výsledek testů považován za nejasný a následoval opakovaný odběr. Proto také doporučuje mít tuto hodnotu menší než 38.
Je tak možné, že alespoň některé falešně pozitivní případy byly spojeny právě s tímto problémem. To ovšem nelze bez přesných údajů zhodnotit. Jak jsem zdůraznil, nejsem navíc virolog nebo genetik. Tuto oblast tak nebudu hodnotit a podívám se na všechna zmíněná data pouze z pohledu statistiky, pravděpodobnosti a podmíněné pravděpodobnosti.
Ještě jednu informaci je třeba před začátkem naší analýzy zmínit. Při pročtení zmiňované studie zjistíme, že pan Dalibor Štys se spletl a prohodil výsledky u vody a chřipky. Falešná pozitivita 3 % byla u vzorku s chřipkou a 4,4 % u vody. Hypotézu, že viry chřipky či rýmy zvyšují pravděpodobnost falešné pozitivity, tak na těchto datech opravdu nelze postavit. Za chvíli si však ukážeme, že tuto hypotézu by nepodpořilo i to původně jim prezentované přiřazení.
Řešení problému si dovolím naznačit a dokumentovat na návrhu příkladu, který bych zadal studentům na cvičení ze statistiky a zpracování experimentu, abych jim objasnil, jaké chyby v uvažování se pan Štys dopustil.
Máme testovací sadu, která identifikuje daný vir a máme tři informace o ní.
1) Výsledky malé studie s negativním vzorkem, při které se při 100 testech objevily 3 pozitivní.
2) Rozsáhlou studii negativních vzorků, kdy se při 100 000 testováních objevilo 1540 pozitivních případů.
3) Výrobce testu udává, že jeho specificita je lepší, než hodnota 0,984.
Můžete říci, zda jsou tyto studie a informace v souladu nebo jsou některé v rozporu?
Čtenáři, kteří se v dané oblasti vyznají a rozumí ji, už tak znají řešení i nastíněného rozporu mezi studii Státního zdravotního ústavu a dat z německých testování.
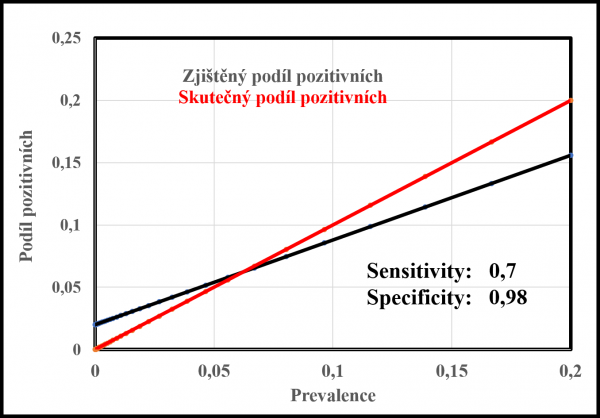
Příklad závislosti podílu zjištěných pozitivních případů a skutečného podílu pozitivních případů na prevalenci pro případ testu se senzitivitou 0,7 a specificitou 0,98.
Podmíněná pravděpodobnost a její paradoxy
Náš problém je spojen s několika klíčovými pravděpodobnostmi. Testování přítomnosti viru může kromě správného výsledku přinést v případě pozitivního vzorku i negativní výsledek. Pravděpodobnost toho, že pozitivní vzorek bude označen správně za pozitivní se označuje jako senzitivita testu. Může však také dojít k tomu, že negativní vzorek bude označen za pozitivní. Pravděpodobnost, že negativní vzorek bude označen správně za negativní se označuje jako specificita. Tyto veličiny jsou klíčové pro kvalitu testu, ale je jasné, že v realitě nikdy nedosáhneme 100 %. Při testování tak máme falešně negativní i falešně pozitivní případy.
Velká část testů je konstruována tak, že má velmi vysokou specificitu. To znamená, že u negativního člověka dostaneme negativní výsledek s vysokou pravděpodobností. Procento falešně pozitivních v souboru testovaných je tak malé a jeho maximální hodnotu dostaneme v případě, že máme populaci bez pozitivních případů. Podíl pozitivních případů je pak rovnen rozdílu mezi 100 % a specificitou. Jde v tomto případě o velmi nízkou hodnotu.
Podívejme se nyní na pravděpodobnost, že pozitivně testovaný je opravdu pozitivní. Ta je extrémně závislá na pravděpodobnosti výskytu nemoci v populaci, která se označuje jako prevalence. Pokud je prevalence výskytu nemoci v populaci velmi malá, je pravděpodobnost, že bude pozitivně testovaný opravdu pozitivní velmi malá. Pokud bude prevalence nulová, bude pochopitelně pravděpodobnost, že je pozitivně testovaný opravdu pozitivní, nulová, protože všichni budou negativní.
To ukazuje na to, že vhodné využití testů závisí na účelu testování a také na tom, jakou prevalenci hledaného znaku v populaci předpokládáme. Pravděpodobnost, že člověk, který byl pozitivně testován, je opravdu pozitivní, bude velice silně záviset na našem výběru množiny testovaných. Mohou existovat znaky, které se vyskytují častěji u pozitivních osob. Pokud tak budeme testovat pouze osoby s těmito znaky, pravděpodobnost, že osoba testovaná jako pozitivní bude skutečně pozitivní, se dramaticky zvýší. Jde v tomto případě o podmíněnou pravděpodobnost.
Krásně se to dokumentuje třeba na testování na alkohol foukáním do trubičky. Zvláště při nízké pravděpodobnosti výskytu těch, kteří pili, se musí počítat s falešně pozitivními výsledky. Pokud tedy pozitivně testovaný řidič nepřizná požití alkoholu, může jít o falešně pozitivního a test je třeba opakovat nebo použít test s vyšší kvalitou, třeba z krve.
To je třeba i důvod, proč policisté prioritně testují účastníky akcí, při kterých se pije nebo v době Velikonoc. Při normální kontrole testuje policista na alkohol většinou pouze řidiče, u kterých z jiných důvodů dostane podezření, že pil. V případě epidemie tak má smysl testovat hlavně ty, kteří mají příznaky nebo byli v kontaktu s nakaženým. To je i důvod, proč je kontraproduktivní masivně testovat všechny.
Existuje však případ, kdy testování ve skupině, kde spíše předpokládáme malý výskyt pozitivity, má velký smysl. Zase si to vysvětlíme na testech na alkohol. Máme profese, jako jsou třeba profesionální řidiči, kde je extrémně důležité, abychom věděli, že nepili. Specificita testu bývá v tomto případě velmi vysoká, takže falešná negativita je při malé prevalenci extrémně malá. Test je tak zárukou, že do provozu nepustíme profesionálního řidiče s alkoholem v krvi. V tomto případě tak může být vhodné přistoupit k plošnému testování skupiny, která má i velmi malou prevalenci. V případě naší epidemie jsou to situace, kdy jde o pracovníky v nemocnicích nebo v sociálních službách. Zde potřebujeme zaručit, že tito pracovníci nepřenesou nákazu na své pracoviště a klienty. Stejně tak má smysl hromadně testovat lidi přijíždějící do země, která zatím nemoc nemá nebo jen s malou prevalencí. Musíme však počítat s jistou pravděpodobností falešné pozitivity. Tu je pak potřeba řešit opakovaným testem nebo využitím kvalitnějšího testu, pokud existuje.
Podívejme se ještě na limitní případy. Pokud budeme mít populaci (vzorky), kde se daný znak (virus) nevyskytuje, bude pravděpodobnost výskytu pozitivně testovaných dána čistě falešně pozitivními a její hodnota bude 100 % mínus specificita. V testu Státního zdravotního ústavu to byly vzorky vody a chřipky. Pokud naopak bychom měli populaci (vzorky), která je stoprocentně infikovaná (vzorky viru), bude podíl pozitivně testovaných dán senzitivitou. Limitní případy nám tedy při dostatečně velkém počtu měření umožňují určit senzitivitu a specificitu testu.
Abychom si lépe ukázali, jak popsané závislosti pravděpodobností fungují, předpokládejme, že máme test se senzitivitou 0,7 a specificitou 0,98. Podívejme se, jak se bude chovat podíl pozitivně testovaných oproti reálnému počtu infikovaných. Při nulovém výskytu bude podíl pozitivně testovaných dán čistě falešně pozitivními a bude 0,02. Pro nulovou a obecněji dostatečně nízkou prevalenci bude počet pozitivně testovaných vyšší než skutečně pozitivních, kterážto situace je k vidění na prvním grafu v oblasti zleva až do bodu křížení obou přímek. Teprve při dostatečné prevalenci začne převládat počet skutečně pozitivních (oblast od bodu křížení doprava). V důsledku nedokonalé senzitivity, která je reálně vždy menší než jedna, bude podíl pozitivních testovaných nižší než reálných.
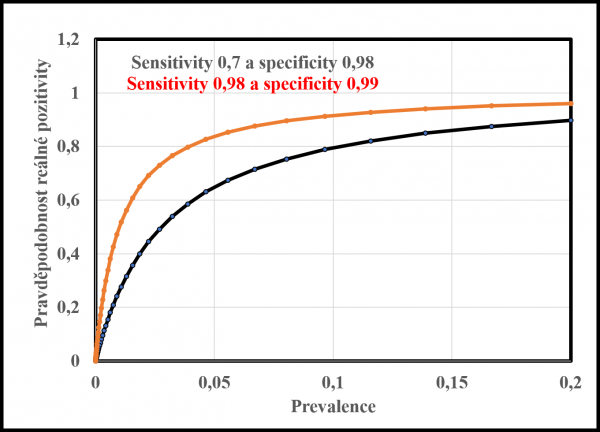
Jak jsme psali, při nulové prevalenci je pravděpodobnost, že pozitivně testovaná osoba je opravdu pozitivní, pochopitelně nulová. S rostoucí prevalencí ale pravděpodobnost toho, že je pozitivně testovaný opravdu pozitivní, začne růst. Růst závisí na hodnotách senzitivity a specificity. V grafu na druhém obrázku je závislost pravděpodobnosti, že bude pozitivně testovaný opravdu infikovaným pro dva případy. Jednak pro senzitivitu 0,7 a specificitu 0,98, ale také pro senzitivitu 0,98 a specificitu 0,99.
Pravděpodobnost, že pozitivně testovaný je opravdu pozitivní v závislosti na prevalenci pro dva typy testů. Černě je test se senzitivitou 0,7 a specificitou 0,98, červeně pak test se senzitivitou 0,98 a specificitou 0,99.
Rozdíl mezi malou a velkou statistikou
Vždy, když máme co do činění s pravděpodobnostními jevy, je pro přesnost našich experimentálních výsledků kruciální statistika našich měření. Ta také určuje statistickou nejistotu námi získaných hodnot. Předpokládejme jev, který připouští s jistou pravděpodobností falešnou pozitivitu. Uděláme stovku měření negativního vzorku a pozorujeme 3 případy falešně pozitivních. Nejpravděpodobnější hodnotou falešné pozitivity je sice 3 %, ovšem v mezích statistických nejistot to může být 2 % nebo 4 % a v rámci tří standardních odchylek i hodnoty velmi blízké nule. A s odpovídající nepřesností z tohoto výsledku můžeme určit i specificitu. V rámci statistických nejistot tak nelze vyloučit žádnou hodnotu v rozmezí 0,94 až 1,00. K tomu, abychom mohli z měření negativních vzorků určit specificitu v oblasti hodnot lepších než 0,98, potřebujeme řádově vyšší počet měření. V každé analýze však musíme vzít v úvahu počet měření a tomu odpovídající statistickou nejistotu. Při studiu šíření infekce a výsledků testů tak narážíme na vliv hodnot senzitivity a specificity. Nejistoty, které přináší, se ještě zvýrazní v případě, když můžeme udělat jen velice omezený počet testů. Velice pěkně to ve svém článku popsala forenzní genetička Halina Šimková s kolegy. Její přednáška, která je podle mě jednou z nejlepších prezentací k problematice podmíněné pravděpodobnosti a testování pro veřejnost, je na konci tohoto článku.
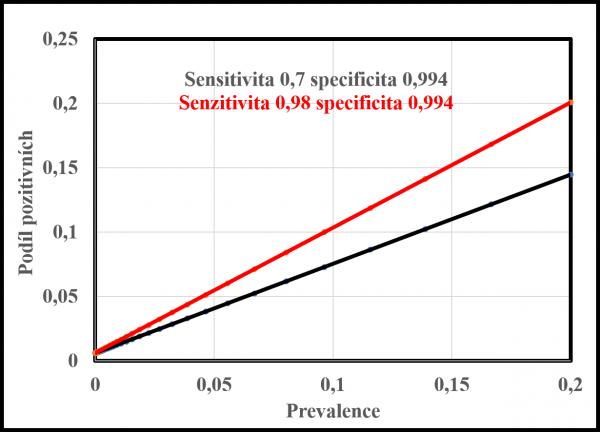
Možnosti testů, které by mohly splnit letní německá data pro podíl pozitivních v celkovém počtu testů. Pro to je důležitá specificita, ta musí být 0,994 (nebo vyšší). To vede u populace bez infekce k pozitivitě 0,6 % (0,006). Ta je čistě falešná. Jsou uvedeny závislosti podílu pozitivních testovaných na prevalenci pro dva extrémní případy sensztivity 0,7 a 0,98.
Jsou data ze Státního zdravotního úřadu v rozporu s německými daty o testování?
Vraťme se teď k hypotéze pana Dalibora Štyse a datům, o které ji opírá. Ze zprávy Státního zdravotního ústavu víme, že z kontrolovaných laboratoří jich 3% falešně identifikovalo vzorek, ve kterém byl virus chřipky místo SARS-CoV-2, a 4,4% jich falešně identifikovalo vzorek s čistou vodou. Pro malý počet testů odpovídajících těmto vzorkům (v testovací sadě jde o 68 testů pro chřipkový vzorek a 69 testů pro vzorek s čistou vodou, a z nich byly postupně pouze 2 a 3 falešně pozitivní výsledky) není výsledek pro chřipku a vodu rozdílný a nejde vyloučit ani hodnoty falešné pozitivity pod 1%, tedy ani specificitu 99,4% vycházejících u německého testování.
V případě německých dat se jedná o desítky až stovky tisíce testů. S takto vysokými počty už můžeme docílit velmi přesné určení specificity. Pokud budeme předpokládat, že v létě byla prevalence viru v populaci velmi nízká, prakticky zanedbatelná, získáme pro specificitu velmi dobrý dolní odhad. Pokud tomu tak není, tak dostaneme alespoň její dolní hranici. Jestliže procento pozitivních testů v Německu kleslo v létě na hodnotu až 0,59 %, pak při uvedeném předpokladu, kdy tato hodnota je tvořena prakticky výhradně falešně pozitivními výsledky, získáme jako odhad specificity hodnotu 99,4 %. To je hodnota, která není v rozporu s možnostmi, které se u těchto testů uvádějí. Testy PCR podle různých zdrojů na internetu mají senzitivitu větší než 70 % ale může být až 98 %. Specifita je větší než 98 % a může být i větší než 99 %. Tady opět zdůrazňuji, že nejsem expert na tyto testy a tady si rád na Oslovi přečtu rozbor někoho povolaného.
Z předchozího textu je zároveň jasný velice pěkný návod na zjištění efektivní specificity používaných testů. Přitom by stačilo využít stávající data. Využila by se data z období, kdy byla prevalence populace nízká, třeba právě první půle léta. A zároveň se vyberou jen ty, které se dělaly v rámci předběžného testování, bez podezření na infekci. Nebo by se vybraly pouze testy lidí, kteří v té době i později nebyli příznakoví. Pochopitelně by bylo nutné provést i další kontrolu toho, aby se do použitého datového souboru nevnesly nějaké korelace, které by výsledek mohly ovlivnit. Podle mě je to pěkné a užitečné téma pro diplomovou práci na nějaké universitě, která se zabývá statistikou a epidemiologií.
Dovolil bych si tak nyní shrnout závěry naší analýzy:
-
Statistické nejistoty určení relativního počtu pozitivních případů ve studii Státního zdravotnického ústavu jsou natolik velké, že v jejich rámci nelze rozlišit mezi hodnotou pro vodu a pro vzorek s chřipkou. Tato studie tak nepotvrzuje hypotézu, že vir chřipky zvyšuje falešnou pozitivitu PCR testů.
-
Z podílu pozitivních testů v letním období v Německu plyne, že efektivní specificita jejich testů je větší než 99,4 %, což není v rozporu s hodnotou ve studii Státního zdravotního ústavu, pokud se vezme v úvahu její statistická nejistota. Nepodporuje to tedy hypotézu, že německá data o podílu pozitivních testů by byla nevěrohodná.
Tyto závěry jsou postaveny čistě na statistické analýze poskytnutých dat. Pochopitelně mohou být testovací data ovlivněna celou řadou dalších faktorů. Ty jsou však spojeny s genetikou, takže je to oblast, ve kterých odborník nejsem. Rád si přečtu článek od odborníka o konkrétních vlastnostech testů a nejistotách spojených s jejich realizací. Konkrétní data v tomto směru, která by podporovala jeho hypotézu, Dalibor Štys neposkytl. Neuvedl také žádná další konkrétní data o německých testech, která by podle něj měla snižovat věrohodnost německých dat.
Závěr
Jak jsem psal v úvodu, na sociálních sítích koluje okolo koronavirové epidemie celá řada nepodložených hypotéz a spekulací. Zaštiťují se různými studiemi. Když se však do uvedených odkazů podíváte, tak zjistíte, že danou hypotézu nepodporují, či ji dokonce popírají. Problém je, že seriózní rozbor každé z nich je časově opravdu velmi náročný. Alespoň jednu jsem se tak snažil rozebrat v tomto článku. Pochopitelně nejde o odborný, ale spíše populárnější text, i když se snaží o co nejvíce korektní postup. Budu tak rád za seriózní kritickou diskuzi a hlavně třeba o články kolegů hlavně z biologických oborů, které by podrobněji pro veřejnost analyzovaly vlastnosti viru a epidemie na základě seriózních dat.
Doporučuji ke zhlédnutí velice pěknou přednášku Haliny Šimkové o problematice testování a podmíněné pravděpodobnosti, kterou měla na akci pro středoškolské pedagogy „Matematika pro život“:
Diskuze: