
Světlo na cestě skrz sklenici s průhlednou kapalinou projde po přímce. V neprůhledné suspenzi ale musí kličkovat následkem různých odrazů na nanočásticích. Cesty rozptýleného světla v takovém objektu jsou složité. Některé jsou kratší a jiné komplikovaně dlouhé. A nyní pozor, přijde to hlavní. V průměru jsou tyto délky světelných cest stejné. To ale znamená, že je u světla jedno, zda prochází sklenicí křišťálově čisté pramenité, nebo mlékem. Nyní se to rakousko-francouzkému kolektivu podařilo dokázat experimentem. Informaci o tom přináší Technická univerzita ve Vídni a prestižní časopis Scinece.
Na publikaci je uveden jako první autor Romolo Savo, Švýcar, toho času ve francouzských službách. Nicméně jde o potvrzení předpokladu, který před třemi léty předpověděl Rakušan Stefan Rotter se svým týmem z Technické university ve Vídni. Podle něj si můžeme světlo zjednodušeně připodobnit k proudu drobných částic. Trajektorie fotonů v kapalině závisí na počtu překážek, které se mu postaví do cesty. Ve zcela průhledné kapalině se částice pohybují podél rovných přímek, a tak také kapalinu na protější straně opouštějí. V neprůhledné kapalině jsou však trajektorie komplikovanější. Světelný paprsek mnohokrát mění směr. Může se dostat až k opačné straně po překonání řady peripetií uvnitř neprůhledné látky, ale také nemusí. A právě v tom je ten zakopaný pes. Mnoho fotonů nikdy na protilehlou stranu nedorazí. Při své „cik-cak“ cestě jich řada pronikne jen krátce pod povrch a poté změní směr a těleso opustí. Když se na to vezme strohá matematika, tak lze teoreticky vypočítat, že se tyto dva efekty vyrovnávají. Průměrná délka dráhy fotonů v kapalině je tudíž vždy stejná a je přitom jedno, zda jde kapalina průhledná, či neprůhledná.

Poněkud komplikovanější situace nastává, když se na světlo přestaneme dívat jako na částici, ale jako na vlnu procházející kapalinou. Tam už je matematický popis situace "vyšší dívčí". Nicméně máme-li věřit matematikům, i v tomto případě dospěli ke stejnému výsledku. Vyšlo jim, že „střední vlnová délka“ spojená s průnikem světla kapalinou je také vždy stejná. A také u ní nezáleží na tom, jak moc je vlna uvnitř media při jeho průchodu rozptýlena.
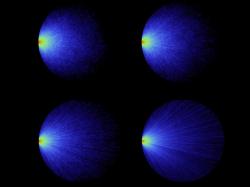
Oba případy, předpovězené už výpočty kolektivu Stefana Rottera v roce 2014, se nyní rakousko-francouzskému kolektivu podařilo podepřít praktickým experimentem. Naplnili zkumavky vodou a pak do nich přidávali nanočástice. Roztok se zakalil a světlo se rozptýlilo. Způsob (směr) jakým se rozptyluje, se v závislosti na postavení nanočástic neustále mění tak, jak se neustále mění úhly odrazu na nanočásticích. Tím ale začne celý vnější povrch zkumavky zářit. Když se tento svit pečlivě změří, dá se z něj odvodit délka dráhy světla uvnitř kapaliny. A to už nejsou teoretické výpočty, ale naměřené hodnoty. A jak jinak, i ony potvrdily platnost teorie, protože průměrná délka dráhy světla zůstávala stejná bez ohledu na to, jak moc bylo prostředí průhledné.
Závěr
To, že se světlo šíří v lahvi mléka plnotučného i toho šizeného stejně, by nám mohlo být v podstatě jedno, nicméně jde tu o potvrzení platnosti univerzální fyzikální zákonitosti a ta platí pro jakoukoliv vlnu. Třeba i na chování zvuku v prachové bouři. Asi nejdůležitější na tom ale je, že podle autorů to platí i pro právě objevené gravitační vlny a jejich šíření vesmírem. Gravitační vlny také tu a tam naráží na galaxie a procházejí jejich „smetím“. Slovy šéfa kolektivu Stefana Rottera: „Základní fyzikální principy jsou i pro ně stejné."
Literatura
Romolo Savo, et al.: Observation of mean path length invariance in light-scattering media. Science 10 Nov 2017: Vol. 358, Issue 6364, pp. 765-768
DOI: 10.1126/science.aan4054
Experiment ATLAS v CERNu poprvé pozoroval rozptyl světla světlem
Autor: Stanislav Mihulka (16.08.2017)
Rychlost šíření gravitačních vln
Autor: Vladimír Wagner (11.11.2017)
Diskuze:
Radio JEREVAN: Je to Svatá Pravda, pokud je obsah sklenice s eirkoňakem nasvícen dokonale homogenně a izotropně, tzv. Lambertianovsky (naprosto difúzním osvětlením, tj. při potlačení optických jevů na rozhraních skla uvnitř i vně), tj. za mlhy a zákazu vy
Josef Hrncirik,2017-11-15 13:03:44
Vidno ostře zříti: viz cca 3. cm ve 3. odstavci v článku, který je možno zdarma stáhnout i se supplements pomocí DOI z Vladimírova SCIHUB.
Vladimíre, díky!
V plochém Lambertiánském osvětlení je zřejmé jedině, že peer reviewers Science neviděli chybné označení legendy k fig.3 na s.3.
Josef Hrncirik,2017-11-15 15:24:57
Na straně 3 ve fig. 3.B i 3.C je nezávisle proměnná pochopitelně úhel theta.
Proměnnou či parametrem pochopitelně NENÍ koncentrace vzorku (která se navíc vůbec nikde nevyskytovala).
Parametrem (či implicitní proměnnou) je transport mean free path l*, které je uvedené jako popisek křivek s daným parametrem l* .
Koncentrace nikoho nezajímají.
Pokud to vůbec četli, či dokonce se dostali až na page 3. Sorry jako.
Josef Hrncirik,2017-11-15 15:45:10
Je to optický klam či jen běžný gentlemanský rozpor mezi slovy a činy, nebo jen politování hodný pracovní úraz z dlouhodobého používání silných laserů?
Josef Hrncirik,2017-11-17 13:38:20
Již v komentáři pod r.1 na s.1 stále píší o nutné podmínce Lambertiniánského difúzního osvětlení a malují ho všude při vstupech i výstupech v obr.1A, 1.C; (1.B je jen funkční závislost).
Při vlastním měření však přeřízli válec kalných vod přesně kolmo napříč světelným listem, získaným bočním rozšířením (průchodem válcovou čočkou) tenkého kolimovaného svazku laserových paprsků.
Pa prsky v listu byly rovnoběžné či prakticky rovnoběžné (vůbec ne difúzní) a difúzní nebyl ani dopad na válec.
Čidlo (jeho otvor (sběr) proměřující úhlovou závislost intenzity rozptýleného světla bylo umístěno do výšky 1 cm nad rovinu pokračování světelného listu, aby nebylo oslněno pokračujícím listem; potlačení středního pásu a záběr úhlu sběru nad rovinou listu světla (záběr do úhlu rozptylu nad rovinou listu) si laskavý čtenář může odečíst a vypočítat z geometrie uspořádání a NA sběrného světlovodného vlákna.
Kde Osel zakoupil obr.2 simulace světelných cest v kruhovém systému s různými stupni opacity?
Josef Hrncirik,2017-11-17 15:37:22
Přestože mám vytištěn článek i supplements, je tam pouze první kruh z oněch 4 oslovských.
Pokud však přeřízli kalné vody světelným šhitem (jak tvrdí), potom a)(v daném bodě) světlo přichází zleva vždy ve stejném úhlu (tj. nikoliv difúzně!) b)normálově jen pro papr-sek procházející kolmo osou válce (tj. v 9 hod) a pak reálné diagramy rozptylu jsou symetrické, avšak výrazně protáhlejší než 4 uvedené simulované z difúzního nasvícení.
Reálný škaredý rozptylový obrazec z bodu ze skoro tečného dopadu paprsků z listu (tj. na okraji kruhu (v 6 či 12 hod) musí silně šilhat útěkem bokem a být velmi asymetrický.
Tyto simulace metodou Monte Carlo vlastně jiných rozptylů, se jim však výborně kryly s vlastně jinak prováděným reálným rozptylem.
V této hazardní hře tedy jasně zvítězili.
Rovnice 1 na 1. straně článku tvrdí, že při Lambertiánském difůzním osvětlení celého objemu je při náhodné procházce světla objemem střední dráha tímto objemem nezávisí na délce náhodného kroku a je rovna 4*objem/povrch. Není jasno, zda to platí i pro pří
Josef Hrncirik,2017-11-23 10:07:24
Střední dráhu přímého průchodu Lambertiánsky osvětlené koule asi matfyzák či matolympionik amatér neřkuli professionál snadno vypočítá určitě pro kouli či desku.
Pro kouli by 4*V/S mělo vyjít 2/3 průměru a pro nekonečnou desku 2*tloušťka.
Re: Rovnice 1 na 1. straně článku tvrdí, že při Lambertiánském difůzním osvětlení celého objemu je při náhodné procházce světla objemem střední dráha tímto objemem nezávisí na délce náhodného kroku a je rovna 4*objem/povrch. Není jasno, zda to platí i pro
Josef Hrncirik,2017-11-27 16:55:16
Pro kouli mi amatérsky vyšlo ĺ = průměr*2/pí; to je jen 95,5% teorie 4*V/S a pro desku to nekonverguje kvůli nekonečnu pro tečný dopad; pokud se nevloudila chybička.
Re: Re: Rovnice 1 na 1. straně článku tvrdí, že při Lambertiánském difůzním osvětlení celého objemu je při náhodné procházce světla objemem střední dráha tímto objemem nezávisí na délce náhodného kroku a je rovna 4*objem/povrch. Není jasno, zda to platí i
Josef Hrncirik,2017-12-10 21:59:22
Pro jimi použitý vysoký sloupec (válec) kapaliny by při L. osvětlení rozptylující kapaliny střední dráha ĺ = 4*objem/povrch = 4*TT*r**2*h/2*TT*r*h = 2*r = d válce.
Pro průchod kolmým světelným listem bez rozptylu ĺ = TT*r*r/2*r = TT*r/2 = d*TT/4
= jen 79% d.
Výrok, že ĺ nezávisí na rozptylu, musí tedy nutně platit jen pro Lambertiánské osvětlení.
Výrok, že ĺ nezávisí na rozptylu pro gravitační vlny by asi taky měl platit pro L. osvětlení grav. vlnami. Toto difúzní osvětlení (izotropní a homogenní) asi není samozřejmé a navíc rozptylová délka gravitačních vln je asi extrémní a index lomu cca 1.
Re: vy vycházek
Josef Hrncirik,2017-11-26 09:52:17
V článku na s.2 ve 3. odstavci cca ´´ odshora sice píší, "vzorek je ozařován pod všemi úhly světelným šitem z laseru .." . Určitě to není Lambertiánské osvětlení do každého bodu vstupu.
Navíc je zřejmé, že to je v rozporu s tvrzením v supplements na s.1 v 8.ř. a v obr.S1B
.. "toto osvětlení (light sheet příčně válcem) poskytuje uniform isotropic light injection in the horizontal plane.."
Přes scihub zdarma na 10.1143/jjap.34.2495 je vidět, že takto se nazývá Lambertiánské osvětlení pochopitelně každého vstupního bodu, buď mimořádně silně konvergentním svazkem ze spojky krátkého ohniska do každého vstupního bodu (relativně malé vstupní plochy), nebo na povrchu vstupu musí být difúzní (rozptylová vrstva).
Pokud vstup rozptyluje až vzorek, jen při velmi silném rozptylu (dlouhé dráze se to začne podobat L. osvětlení).
42
Jakub Beneš,2017-11-15 01:57:52
tento experiment bych popsal jako: "tak dlouho jsme hledali zadání, až nám to vyšlo".
Vůbec nevím o čem je řeč
Gravitační Teoretik,2017-11-14 16:15:31
Představuji si takové to dlouhé molo, které vede do moře a pod ním běží vlna, která sice naráží na sloupy mola, ale přitom se neláme, neohýbá ani nebrzdí, molo nemolo, vlna si razí cestu dál a pilíře mola jsou pro ni irelevantní. Jestli to nějak souvisí.
Pavel Pelc,2017-11-14 15:23:15
Z toho, ze je stredni draha stejna, prece vubec neplyne, ze se svetlo siri stejne ve sklenici mleka i ve sklenici vody.
Přes pole blíž...
Jiří Raur,2017-11-14 14:25:35
Nadpis podle mě neodpovídá zkoumané realitě. Přes pole bych se tímto způsobem ve většině případů do původního cíle, na druhém konci pole, nikdy nedostal. Pokud mi bude jedno, kam se přes pole dostanu, tak mohu být v novém cíli, hned vedle startu, opravdu dříve.
Jednoduše jde o jiné zadání: Občas v tomto novém cíli budu stejně rychle a občas později. Ve všech případech se budu pohybovat rychlostí jako po silnici. Jde tedy spíš o vyasfaltované náměstí s chodci (nano částice) a jedu na kole a vyhýbám chodcům tak dlouho, než narazím do zdi (nebo vyjedu z náměstí ven). V průměru to prý bude stejně dlouho, jako přímo napříč náměstím, když tedy nebude nikdo v cestě.
Já bych osobně volil silnici kolem náměstí, bez chodců, třeba i delší. Konečně tak to běžně ve městech dělají, že se náměstí objede.
Prosím o vysvětlení
Petr Beznadějný,2017-11-14 11:19:14
Co kdyby pokus pracoval s tímto tvarem nádoby:
https://image.ibb.co/eKy23G/Nov_rastrov_obr_zek.jpg
Když by nejkratší cesta vedla přímo a "zbloudilé" fotony by musely jít delší cestou, tak se o stejné průměrné délce průchodu mluvit nemůže.
Re: Prosím o vysvětlení
Gravitační Teoretik,2017-11-14 11:37:27
Jestli tomu dobře rozumím, tak zprůměrovaná vzdálenost je všude stejná, to je vlastnost průměru, je všude stejný.
Re: Prosím o vysvětlení
Florian Stanislav,2017-11-14 22:24:14
Nádoba uprostřed tenčí je zajímavá a Vaše námitka vypadá rozumně, že záleží na tvaru.
Nicméně článek uvádí, že byla použita zkumavka. Kapalina ve zkumavce se skládá řekněme z válce + poloviny koule u dna. Paprsky podle schématu nahoře jdou kolmo k ose válce. Horní část zkumavky je ukončena rovinou a spodní polokoulí. Nádoba je tedy asymetrická k paprsku a měření odpovídá teorii stejné dráhy v kapalině s nanočásticemi.
Nedovedu si představit, že by někdo teoreticky zkoumal a pak složitě měřil tento jev, aniž by uvedl, že výsledek platí jen pro určitý tvar. Snad mohu připomenout hydrostatické paradoxon, kdy hydrostatický tlak nezávisí na tvaru nádobdy, ale jen na výšce sloupce.
První věta článku o tvaru kapaliny nemluví:"Světlo může procházet přes průhlednou kapalinu přímo, nebo krkolomně klikatými cestami v suspenzi (kapalině s rozptýlenými nanočásticemi), délka jeho cest je v obou případech stejná."
Re: Prosím o vysvětlení
Petr Matas,2017-11-15 17:56:01
Cituji z abstraktu článku: "Theory predicts that exciting such a medium homogeneously and isotropically makes some of its optical properties depend only on the medium’s outer geometry." Takže to nefunguje, když se na nádobu posvítí jen z některých směrů. Musí se svítit ze všech stran stejně, tzn. obklopit ji zdrojem světla konstantního jasu.
Gravitační vlny
Gravitační Teoretik,2017-11-14 10:16:11
K té aplikaci na gravitační vlny
Hypotéza: Gravitace je univerzální i Univerzální dostředná síla. Pohybem těles je zcela spotřebována, nevznikají v ní zpětné rázy, ozvěny, které by šly odstředně, proti proudu a tvořily gravitační vlny. Je to pohon vesmíru, který se bezezbytku transformuje na pohyb. V té přeměně nejsou zbytkové energie, které by se vracely zpět a tvořily "odražené vlny", gravitace je bezezbytku spotřebovávána. Gravitace je tlak prostoru na hmotu. Prostor, pole, vakuum, má svojí soudržnost, kterou hmota v něm rozmístěná rozrušuje. Prostor je dlaň a hmota namydlené vejce. Dlaň tiskne, vejce se pohybuje směrem nejmenšího odporu. Sousedící hmoty, částice, planety, jedna druhé sobě navzájem vytváří komplementární vzájemný vztah nejmenšího odporu, a proto "se přitahují", to vše při trvalé tendenci rozpínat se, jelikož rozpínání není nic jiného, než vedlejší důsledek dostředné síly prostoru.
Re: Gravitační vlny
Gravitační Teoretik,2017-11-14 11:11:21
Kontrahypotéza:
Černá díra je 100%ní zahuštění hmoty. Sousedící černé díry, které se před splynutím dotýkají svými okraji, mezi sebou mají tenkou membránu prostoru, která při jejich splynutí praská a vytváří spojnici, "červí díru" mezi černými díramy, kterou se hmota obou černých děr spojí, slije v jednu. Tato "červí díra" při svém rozširování, v průběhu slévání černých děr, může vytvořit efekt gravitačního třesku, rázu, který putuje v protisměru a může vytvářet lokální zvlnění, zpětný ráz. Ovšem pouze o jedné jediné amplitudě. Do okamžiku otevření "červí díry" spojující dvě černé díry je gravitace spotřebovávána. I tento "třesk" je diskutabilní, jelikož může jít o plynulý proces, při kterém nevzniká žádná náhlá změna stavu. Hmota černých děr může vytvořit při splynutí okamžité protichůdné gravitační působení, s opačným vektorem, tj. odstředným. Jaký dosah a trvanlivost taková vlna má, těžko hádat. Je to stejné, jako kdybyste chtěli poslat vlnu proti proudu řeky.
Re: Re: Gravitační vlny
Petr Matas,2017-11-15 18:20:12
Vaše hypotézy jsou zajímavé, ovšem nyní byste si měl položit následující otázky:
1) Jsou předpovědi Vaší teorie v souladu s pozorováními? Dokáží vysvětlit gravitační čočky a velikost stáčení perihelu Merkuru? Jsou ve shodě se signály zaznamenanými detektory LIGO a VIRGO? Obecná teorie relativity (OTR) ano.
2) OTR sestává z pár rovnic a dvou konstant (gravitační konstanta a rychlost světla). Není Vaše teorie složitější než OTR? Nebo je alespoň v lepším souladu s pozorováními než OTR?
Roman Madala,2017-11-14 06:16:13
Keby sme vystrelili miliardu rakiet do vesmíru jedným smerom, tiež by sme predpokladali, že všetky narazia do nejakej hviezdy?
Jak
Jan Vlačiha,2017-11-14 03:11:39
Jak se to bude měnit s postupným zvětšováním odrážejících částic?
Netvrďte, že výsledek bude stejný, když v čirém roztoku zůstane jen pět velkých zrcátek.
Protipříklad
Petr Matas,2017-11-13 22:48:45
Myslím, že mám myšlenkový experiment, který tvrzení uvedené v článku vyvrací: Vezměme velmi vysokou zkumavku (výška >> průměr) plnou kapaliny a posviťme na ni shora úzkým paprskem v její ose. Čirou kapalinou světlo proletí přímo až na dno zkumavky a dráha světla v kapalině bude rovná výšce zkumavky. Naproti tomu ve velmi kalné (avšak nepohlcující) kapalině se světlo rozptýlí, takže většina jej opustí zkumavku do stran. Do blízkosti dna se nedostane prakticky žádné. Průměrná délka dráhy světla v kapalině tedy v tomto případě nebude záviset na výšce zkumavky. Průměrné dráhy v čiré a kalné kapalině se tedy nemohou rovnat.
Něco jsem špatně pochopil nebo na něco zapomněl? Autoři mají svá tvrzení určitě dobře podložená...
Re: Protipříklad
Florian Stanislav,2017-11-14 09:07:11
Já to chápu tak, že odraz ve Vaší dlouhé zkumavce nenastává hned na začátku roztoku ( to by bylo zrcátko), ale průběžně a jde i do hloubky. Průměrná jakoby dráha přímá je tedy půl délky zkumavky. Ve skutečnosti je dráha lomená a tedy delší. Druhá část dráhy je součet drah rozptýlených do stran, tedy průměrně kratších. Počítá se vážený průměr, lépe se mi chápe, že se rovná součet celkových drah v propustném roztoku součtu v roztoku s nanočásticemi. Článek to ale jasně říká, že kratší pryč rozptýlené a delší uvnitř zalomené dráhy se kompenzují.
Fotony světla nejsou nanočásticemi ( podle definice 1-100 nanometrů) pohlcovány, ale obtékány, světlo viditelné má zhruba 390-780 nm. V článku uvedený příklad prach a vlnění zvuk je něco podobného, vlnová délka je větší.
Obrázek na začátku je převzatý ze zdroje. Názornější by mi přišlo, kdyby v levé části byly procházejíc paprsky dva, oba projdou přímkově. V pravé části jeden paprsek kličkuje zdatně uvnitř, druhý se brzy odrazí ven, součet drah dvou paprsků schématu pak vizuálně bude srovnatelný. Prostě součet drah každé dvojice paprsků bude stejný, tedy i průměrná dráha.
Velikost částic vzhledem k délce vlny mi připadá důležitá. Koloidní roztoky světlo propouští i rozptylují ( Tyndalův jev).
Ale takové mléko a jeho kapičky tuku jistě světlo pohlcují. Pak dráha závisí na tom, jak moc pohlcují, protože tím víc fotonů se pohltí už na začátku roztoku a tím jejich dráha skončí.
Re: Re: Protipříklad
Petr Matas,2017-11-15 17:52:02
Tak už jsem na to asi přišel: Rozhodující je následující věta z abstraktu článku: "Theory predicts that exciting such a medium homogeneously and isotropically makes some of its optical properties depend only on the medium’s outer geometry." Takže to nefunguje, když se na zkumavku posvítí jen z některých směrů. Musí se svítit ze všech stran stejně, tzn. obklopit ji zdrojem světla konstantního jasu. A pak už záleží jen na jejím tvaru, nikoli na kalnosti média.
Re: Re: Re: Protipříklad
Marek Fucila,2017-11-16 11:49:36
To skôr naopak. Ako by sa to meralo, keby sa svietilo zo všetkých strán? Tiež som si nebol istý pojmami homogénny a izotropný, tak z goolenia:
homogeneous : the property is not a function of position, i.e. it does not depend on xx, yy or zz.
isotropic: the property does not depend on a particular direction.
https://physics.stackexchange.com/questions/153008/what-is-difference-between-homogeneous-and-isotropic-material
Čiže je jedno, z ktorej strany sa na skúmavku zasvieti a pod akým uhlom. Výsledok závisí od geometrie. A tam je podľa mňa odpoveď na váš myšlienkový experiment: funguje to len ak je to kruhová skúmavka a svietite zboku (a je jedno pod akým uhlom a z ktorého smeru). Pri svietení zhora máte podľa mňa pravdu.
Feynman vo svojej knihe QED vysvetľuje optiku cez dráhy fotónov a času ktoré strávia v médiu (takýmito odrazmi). Do ohniska prídu fotóny v rovnakom čase, ale dráhy boli rôzne - stredom spojky sa svetlo zdrží v skle najdlhšie, a tak priamy lúč dopadá do ohniska v rovnakom čase ako ten, čo sa zlomil na jej okraji a ide dlhšiu dráhu po vzduchu.
Ak tomu správne rozumiem, nie je to ani tak konkrétne o svetle (na tom to experimentálne potvrdili, ale už sa spomína aj zvuk), ale o matematike - aké je štatistické rozloženie dráh rovnomerne rozmiestnených prekážok na kruhovej ploche. Alebo niečo v tom zmysle.
Re: Re: Re: Re: Protipříklad
Marek Fucila,2017-11-16 12:28:22
Tak pozerám obrázok na sci-hube a zjavne merali aj dráhy, ktoré išli mimo rovinu. To ale stále neznamená, že to platí aj pre svietenie zhora/zdola valca, alebo pri jeho spodnom/vrchnom okraji. Ak platí, čo namerali, tak v tomto prípade pre "nekonečný" valec.
Re: Re: Re: Re: Protipříklad
Petr Matas,2017-11-16 14:15:31
Homogenního a izotropního vybuzení média se dosáhne právě tím stálým svícením ze všech stran. Při měření pochopitelně budete svítit jen z jedné strany, možná tím úzkým paprskem do jednoho místa (co takhle záblesk femtosekundovým laserem?). Takhle sice to médium nevybudíte homogenně a izotropně, ale když zprůměrujete výsledky přes paprsky vstupující do zkumavky postupně všemi body na jejím povrchu a pod všemi úhly, pak se doberete té hodnoty, o kterou v článku jde. Mělo by to fungovat pro jakýkoli tvar zkumavky, klidně i nekonvexní, jako třeba v příspěvku Petra Beznadějného výše.
Když se mluví o optice a ohniscích, řekl bych, že se bude pracovat jen s čirými médii. Určitě je vám totiž zřejmé, že dalekohled s průsvitnými (tedy nikoli průhlednými) čočkami by moc nefungoval.
Re: Re: Re: Re: Re: Protipříklad
Marek Fucila,2017-11-20 11:01:30
To, či to funguje s akúmkoľvek tvarom zkúmavky je práve otázne. Píšu tam, že niektoré optické vlastnosti závisia iba na vonkajšej geometrii média. Tie vlastnosti čo namerali merali na valci. Možno tak ako píšete. Má to hlavu a pätu. Ako sa budú správať v nekonvexnej skúmavke pokus neriešil. (Aspoň si myslím.) Druhá vec je, že overovali nejakú teóriu, ktorú nepoznám, a tak ak tá tvrdí, že na tvare nezáleží, je možné, že máte pravdu.
Nie som fyzik ale z toho mála čo viem by som povedal, že priehľadnosť/priesvitnosť je skôr o množstve svetla, ktoré médium pohltí. Ani číre sklo neprepustí všetko svetlo. Ale aj to, čo sa dostane von išlo v materiáli pomalšie ako by išlo vo vákuu. A dôvod spomalenia by mala byť interakcia s elektrónmi. Zjednodušene povedané, fotóny, ktoré zo skla vylenia poväčšine nie sú tie isté, ako tie, čo doň vletia. To, čo som písal o šošovke zobrazuje tento obrázok:
http://www.jasonsummers.org/wp-content/uploads/2010/02/lense.jpg
Pre kontext je celý článok tu: http://www.jasonsummers.org/the-basics-of-quantum-electrodynamics-qed/ Ten som ale nečítal, zrejme stručnejšie popisuje to isté čo kniha ktorú som vyššie spomenul.
Průchod světla disperzí.
Vlastislav Výprachtický,2017-11-13 17:50:41
Nepochybuji o výsledku, ovšem prostorová hustota světelného toku se změní apolu se zářivým tokem.
Re: Průchod světla disperzí.
Milan Krnic,2017-11-13 21:19:35
Já také nepochybuji, ale nějak to v článku uvedené nechápu. Světla se vyzáří pokaždé stejně podle mé logiky proto, že je tam v obou případech (čiré / zakalené) podobně fotonů (a je jim buřta, kolikrát se odrazí). No a reálně (senzoricky) zaznamenávat, kolikrát se odrazili, to je snad sci-fi.
Re: Re: Průchod světla disperzí.
Petr Matas,2017-11-13 22:16:19
Počet odrazů se pochopitelně nezaznamenává. Měří se čas od okamžiku vstupu fotonu do kapaliny do jejího opuštění. A ten může být od nuly (když se hned po vstupu odrazí zpět) do nekonečna (když se důkladně zamotá).
Co se týče množství světla: Asi se předpokládá, že každý foton, který do kapaliny vstoupil, ji nakonec zase někudy opustí, tzn. žádné pohlcování.
Re: Re: Re: Průchod světla disperzí.
Jakub Beneš,2017-11-15 02:08:50
fakt by me zajimalo jak muzou merit cas od vstupu do opusteni pro jednotlive fotony, kdyz v okamziku vystupu, po x odrazech (odraz je vzdy pohlceni a vyzareni) to je uz uplne jiny foton ;-) tam ta cast o mereni kolem cele nadobky je kriticky moment celeho experimentu a mam o nem pochybnosti.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce




