Když jsem psal o první detekci gravitačních vln experimentem aLIGO (zde a zde), zmínil jsem se, že by to bylo splnění jednoho z mých klukovských snů. I když se mi data zdála velice přesvědčivá a kolegové, kteří se obecnou teorií relativity a gravitačními vlnami zabývají, plesali nad tím, jak pozorovaný signál odpovídá předpokladům, přece jen jsem si nechával zrnko pochybnosti. Problém je, že splynutí černých děr je pozorovatelné právě jen prostřednictvím gravitačních vln. Nebylo tak možné potvrdit danou událost jiným přístrojem.
První zaznamenaná událost byla ulovena velice brzy, ještě při testech před oficiálním zahájením provozu vylepšené verze detektoru LIGO. To by mělo znamenat, že takové události jsou velice pravděpodobné a detektor s danou citlivostí by je měl zaznamenávat relativně velice často. To znamená, že se daly očekávat další případy zachycené systémem aLIGO. Pokud by nebyly, vrhalo by to na publikovaný případ stín podezření.
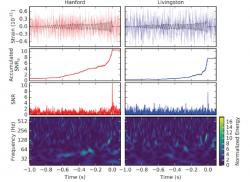
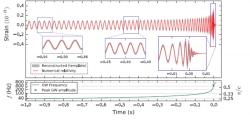
Už v té době se proslýchalo, že spolupráce aLIGO takové případy má a potřebuje je jen co nejpečlivěji zanalyzovat a ověřit. To se potvrdilo v publikaci v časopise Physical Review Letter, která vyšla ve středu 15. června 2016. Tentokrát šlo o případ zaznamenaný 26. prosince 2015 ve 4:39 SEČ a jeho označení tak je GW151226. Signál trval zhruba 1 sekundu a jeho frekvence se měnila od 35 po 450 Hz. Maximální relativní amplituda byla 3,4∙10-22, což je velmi blízko úrovni šumu. Pozorování tak bylo možné jen proto, že bylo pozorováno mnohem více oběhů než v prvním případě. Posun detekce mezi dvěma detektory byl 1,1 ms.
Analýzou signálu se zjistilo, že jde o splynutí dvojice černých děr s hmotnostmi 14,2 a 7,5 hmotností Slunce. Hmotnost vzniklé černé díry byla 20,8 hmotností Slunce. Okolo jedné hmotnosti Slunce se tak přeměnilo na gravitační vlny. Ze srovnání této energie a výsledného gravitačního signálu bylo možné odhadnout vzdálenost černých děr od Země. Ta byla okolo 1,4 miliardy světelných let. Chyba určení této vzdálenosti však byla okolo 40 %, To znamená, že byla v mezích nejistot shodná se vzdáleností předchozí dvojice černých děr.
Kromě těchto dvou velmi průkazných případů se pozoroval v tomto pozorovacím období, které probíhalo od 12. září 2015 do 18. ledna 2016, pouze jeden další kandidát na splynutí dvojice černých děr s hmotnostmi mezi 4 až 100 hmotností Slunce. Případ nastal 12. října 2015 a má označení LVT151012.
Analýza případu GW151226 byla mnohem náročnější než u případu GW150914, protože byl signál slabší. Pomohlo však, že trval déle a bylo možné pozorovat až 27 oběhů soustavy před splynutím. I tak bylo získání signálu na pozadí šumu velmi těžké. To byl i důvod, proč bylo potřeba s jeho publikací počkat. Menší hmotnosti a delší průběh umožnily na druhé straně podrobnější testování obecné teorie relativity. I tento případ je s ní v perfektním souladu.
Za sebe mohu říci, že publikace splňuje to, co jsem očekával, a nyní se už těším, až se znovu soustava aLIGO koncem roku 2016 rozběhne a časem ji doplní i vylepšené VIRGO. Kombinace tří detektorů už by měla umožnit určení relativně přesné polohy zdroje. Pak můžeme očekávat pravidelný přísun případů různých dvojic černých děr, což umožní získat velice dobrou představu o jejich vlastnostech a výskytu i rozložení v našem vesmíru. Jde o fantastickou představu, kterou by ještě před pár lety jen málokdo čekal.
Byly už konečně přímo pozorovány gravitační vlny?
Autor: Vladimír Wagner (11.02.2016)
Detekce gravitačních vln – první dojmy
Autor: Pavel Bakala (12.02.2016)
Evropa na cestě k vesmírné detekci gravitačních vln
Autor: Vladimír Wagner (16.02.2016)
Diskuze:
Opuštění černé díry
David Oplatek,2016-06-19 09:03:12
Měl bych dotaz, zda by bylo hypoteticky možné u velké černé díry, kde je velký Schwarzschildův poloměr (a tedy dostatek času), za horizontem událostí vytvořit červí díru a tím z černé díry uniknout?
Re: Opuštění černé díry
Pavel Brož,2016-06-19 11:01:10
Nejspíše ale do jiného vesmíru, který by vznikl rozfouknutím druhého konce červí díry a posléze jejím zaškrcením. Tento mechanismus vzniku nových vesmírů, tj. vytvořením červí díry, která při svém vzniku vytvoří na druhém konci rozpínající se prostorovou bublinu, rovnice obecné teorie relativity připouštějí. Vytvoření červí díry spojující dvě oblasti téhož vesmíru sice teoreticky možný je, ale vynutil by si složitou kooperaci už během vzniku dvou blízkých rotujících černých děr. Pokud by se jednalo už o existující černou díru, tak z jejího vnitřku není šance vytvořit tunel do oblasti nad jejím horizontem. Vznik černé příp. červí díry můžete totiž ovlivňovat jenom pokud jste nad příslušným horizontem, pokud jste ale už pod ním, tak už nic neovlivníte.
Re: Re: Opuštění černé díry
David Oplatek,2016-06-19 13:59:33
Nebylo by možné se touto vytvořivší červí dírou spojit s jinou černou dírou, která by vyústila také už za horizontem? A během "cesty" do této druhé černé díry z červí díry uniknout, pokud tedy uniknout lze.
Re: Re: Re: Opuštění černé díry
Pavel Brož,2016-06-19 18:07:54
Takhle, je dobré si hned na začátku ujasnit, že se bavíme jenom o divokých spekulacích, které obecná teorie relativity sice za velice speciálních podmínek formálně umožňuje, ale bůh ví jaká skutečná omezení mohou reálně nastat. Jedna z podmínek, aby bylo možné červí díru spojující dvě oblasti našeho prostoru vytvořit, a aby se přitom sama nezničila už během průchodu prvního tělesa, je mít k dispozici dostatečné množství tzv. záporné hmoty. Není to antihmota, je to hmota mající zápornou hmotnost a generující záporný tlak. Formálně má potřebné vlastnosti tzv. temná energie, ale o té nic nevíme, kromě toho, že se má na kosmologických vzdálenostech projevovat zrychlováním expanze vesmíru. Jinými slovy, žádnou takovou použitelnou hmotu k dispozici nemáme, a hned tak mít nebudeme.
Pokud takovouto hypotetickou hmotu máte v dostatečném množství, tak s pomocí ní můžete teoreticky vytvořit červí díru během vzniku její mateřské černé díry (černá díra je v tomto případě pouze ústím červí díry, zvenčí ale vypadá v podstatě stejně, jako běžná černá díra). Negativní hmotu potřebujete ke stabilizaci červí díry, pouze s jejím přispěním totiž můžete zabránit zaškrcení červí díry a jejímu zániku už během průchodu prvního tělesa. Po průchodu červí dírou Vás to vyhodí na druhém konci, tzn. u opačného ústí, které se Vám bude jevit jako tzv. bílá díra - což je formální opak černé díry, ze které částice naopak vyletují ven. Matematicky není mezi černou a bílou dírou žádný rozdíl, pro obě platí, že pokud jste pod horizontem, tak nemůžete změnit směr svého letu v tom smyslu, že buď nezadržitelně padáte dovnitř (případ černé díry), nebo nezadržitelně "padáte" ven (případ bílé díry).
Pokud nějak propojíte červí díru s druhou černou dírou pod horizontem té druhé černé díry, tak hypoteticky získáte konstrukci, kdy na jedné straně máte jako ústí červí díry první černou díru, a druhý konec červí díry Vás může buďto vynést druhou černou dírou ven (tzn. ta by se Vám jevila jako bílá díra), nebo Vás navede do singularity uvnitř té druhé černé díry. Pak byste teoreticky naopak při pádu do druhé černé díry mohl buďto spadnout do její singularity nebo vylétnout tou první černou dírou. Je otázka, jestli takovouto konstrukci rovnice obecné teorie relativity vůbec připouštějí - osobně bych si tipnul, že ano, ale pochybuji, že se takovýmito věcmi někdo reálně zabývá. Ony už obyčejné červí díry budou ještě hóóódně let hodně velkou scifi, natož pak takovéto konstrukce.
Re: Re: Re: Re: Opuštění černé díry
David Oplatek,2016-06-19 23:54:21
Mnohokrát vám děkuji za vyčerpávající odpověď, teď je mi to už jasné.
Zeptám se ještě na poslední věc, co mne zajímá: nedávno jsem četl, že je potřeba pro udržení červí díry mnohem méně antihmoty, než se původně soudilo. Soudě podle vašeho příspěvku, se tedy jedná o zmiňovanou tzv. zápornou hmotu s odlišnými vlastnostmi, a ne antihmotu, což by tedy znamenalo, že autoři článků, které jsem četl, prostě jen termín pro zápornou hmotu z angličtiny nesprávně přeložili jako antihmotu?
Re: Re: Re: Re: Re: Opuštění černé díry
Pavel Brož,2016-06-20 10:26:20
Ano, je to přesně jak píšete, k udržení červí díry je potřebná negativní hmota, ne antihmota, sám jsem se stejně jako Vy setkal s chybnými překlady, kdy negativní hmota byla špatně přeložena jako antihmota. Antihmota je ve skutečnosti co se týče gravitačních účinků nerozlišitelná od hmoty, např. černé díry se zvětšují úplně stejně bez ohledu na to, jestli do nich padá hmota nebo antihmota, a černá díra vzniklá hypotetickým kolapsem antihmoty je nerozlišitelná od černé díry vzniklé kolapsem hmoty.
Menší a větší
Michal Kejík,2016-06-16 21:41:37
Možná historie u obou detekovaných případů je myslím dvojhvězda obřích hvězd - supernovy a vznik černých děr - postupné přibližování s vyčištěním akrečních disků - konečné splynutí. To se může dít relativně často, s rostoucí citlivostí půjde zachytit i menší hmotnosti či větší vzdálenosti.
U černých děr větších velikostí ke splývání zřejmě dochází také, i když mnohem vzácněji. Obzvlášť zajímavé by bylo splynutí obřích děr po srážce galaxií, ke kterému dříve nebo (spíš mnohem) později musí dojít. Dokázaly by detektory vzhledem ke svému frekvenčnímu rozsahu tuto událost zachytit?
Re: Menší a větší
Pavel Brož,2016-06-18 17:10:26
Ne, bohužel současné detektory by takovou událost nedokázaly zachytit, protože by byla v úplně jiné frekvenční oblasti. Abychom došli k odhadu, jaké frekvence můžeme očekávat pro splynutí gigantických černých děr v jádrech cizích galaxií, je zapotřebí nejprve vzít v potaz to, že srážka dvou černých děr není svým způsobem tak katastrofickou událostí, jako je třeba srážka neutronových hvězd. U neutronových hvězd se totiž jejich hmota nachází nad horizontem, takže při jejich srážce dochází k jejímu přímému kontaktu - těsně před srážkou se obě tělesa výrazně deformují působením slapových sil, a při srážce samotné kusy hmoty vystřelují všemi možnými směry, tak jako u každého pořádného karambolu. Prostě nic elegantního, navíc se jedná o děj přesně prakticky nevypočítatelný, protože v procesu tříštění obou neutronových hvězd hraje velkou roli náhoda. Oproti tomu srážka dvou černých děr je mnohem elegantnější proces, připomínající mnohem více splynutí dvou vodních vírů do jednoho - žádné cákance hmoty do okolí (koneckonců hmota obou černých děr už byla dávno pod příslušným horizontem), a i ty generované gravitační vlny mají sice velkou amplitudu, ale nikoliv velkou frekvenci.
U toho posledního, totiž frekvence gravitačních vln generovaných v procesu splynutí černých děr, se nyní zastavme. Z matematického hlediska jde o evoluci dvou řešení, každé charakterizované škálou odpovídající gravitačnímu poloměru, do řešení jednoho. Tato evoluce probíhá ve shodě s Einsteinovými rovnicemi gravitačního pole, což jsou parciální nelineární rovnice druhého řádu (aspoň že v druhých derivacích jsou lineární), tedy není to nic snadno řešitelného (analytická řešení jsou známa jen pro velice málo speciálních případů, mezi které splynutí černých děr bohužel nepatří). Bez ohledu na tyto zmíněné obtížnosti ani zde neexistuje důvod, proč by tato evoluce měla generovat výrazně hodně vln o vlnových délkách výrazně menších, než je gravitační poloměr.
Konkrétně v případě v článku popisovaného splynutí šlo o černé díry s pravděpodobnými hmotami cca 14 a 7 hmot Slunce, tzn. s gravitačními poloměry cca 42 a 21 km, pro jednoduchost berme 30 km. Vzdálenost 30 km urazí světlo (a tedy i gravitační vlna, jelikož i ta se pohybuje rychlostí světla) za desetinu milisekundy, takže bychom mohli očekávat, že maximální frekvence vygenerovaných vln by mohla být řádově deset tisíc Hz. Ve skutečnosti se maximální frekvence těchto vln pozorovala jen 450 Hz, tedy zhruba dvacetkrát menší. Z toho si lze udělat hrubou intuitivní představu, že vlnění prostoročasu v okolí splývajících černých děr nebude zase až taková divočina. Samozřejmě, amplitudy těch vln budou dostatečné, aby ve svém okolí např. drtily pevné konstrukce nebo výrazně deformovaly blízké planety či hvězdy, frekvence těchto vln ale nijak extrémní nebude. Katastrofičnost těchto vln bude podobně jako u vln cunami spočívat v jejich "mohutnosti", nikoliv v krátkosti jejich vlnové délky.
Pokud tento odhad přeneseme na případ hypotetického splynutí gigantických černých děr v jádrech cizích galaxií, které mají hmotnosti typicky miliónů až desítek miliard Sluncí, tj. gravitační horizonty cca sto tisíckrát až miliardkrát větší, než v předešlém případě, tak nám z toho vychází očekávatelná maximální frekvence řádově 0,1 Hz až 0,00001 Hz (skutečná může být opět ještě o řád menší), a pro tuto frekvenční oblast nejsou stávající detektory citlivé. Proto by takovéto splynutí určitě nezaznamenaly.
Na druhou stranu je dobré vzít v potaz i to, jestli lze splynutí gigantických černých děr vůbec reálně očekávat. Důvodem je naprosto odlišná evoluce dvojic černých děr hvězdných velikostí od dvojic gigantických černých děr. Nejpravděpodobnějším vznikem dvojice černých děr hvězdných velikostí je jejich evoluce z dvojhvězd, které na počátku nejsou příliš blízko sebe. Dvojhvězd existuje v galaxiích srovnatelně hodně jako samostatných hvězd, tedy mnoho. Při dostatečné hmotnosti obou se nezávisle mohou časem zhroutit do černých děr (ať už v průběhu exploze supernovy nebo v důsledku akrece hmoty na povrch neutronové hvězdy, pokud toto stadium předcházelo). Potom už stačí jenom počkat dostatečně dlouhou dobu, až při svém oběhu splynou. Existují samozřejmě i jiné mechanismy vzniku vázané dvojice černých děr, právě popsaný bude ale nejpravděpodobnější.
Oproti tomu vázaná dvojice gigantických černých děr vzniká nejpravděpodobněji při splynutí dvou galaxií, pokud v centru každé z nich mezitím vyrostl příslušný budulínek. Typická galaxie, má-li být rodičem gigantické černé díry, má rozměr jako naše Mléčná dráha, či lépe ještě větší, počítejme tedy aspoň sto tisíc světelných let. Při splynutí galaxií budou jejich centrální černé díry od sebe vzdáleny aspoň tisíce světelných let. Gravitační zrychlení působené černou děrou o hmotnosti deseti miliard Sluncí na vzdálenost jednoho tisíce světelných let je desettisíckrát slabší, než gravitační zrychlení působené Sluncem ve vzdálenosti Jupitera - tedy natolik slabé, že doba oběhu obou černých děr kolem sebe budou řádově milióny let. Nelze zde tedy očekávat projev nějakých nelinearit gravitačního pole, jaké způsobují např. zkracování oběžné doby u dvojic černých děr hvězdných velikostí. Pokud zde nedojde k nějakému jinému mechanismu, který oběh obou černých děr zbrzdí (k tomu by mohlo dojít např. v důsledku jejich kolizí s aspoň takovým množstvím hmoty, jako samy váží, spíše řádově více), tak potom lze očekávat splynutí takto mohutných černých děr až v časech řádově větších, než je stáří našeho vesmíru.
Galaxií je v našem pozorovatelném vesmíru sice hodně, na druhou stranu v každé galaxii je bezesporu o několik řádů více dvojic černých děr hvězdných velikostí než potenciálních dvojic gigatických děr. Pokud přijmeme odhad, že těch prvých můžeme detekovat po vylepšení přesnosti detektorů cca 10 za rok (přičemž už dnes jsme schopni je detekovat ze vzdáleností miliard světelných let), tak u těch druhých můžeme přinejlepším očekávat jednu událost za století, spíše ještě za delší dobu (samozřejmě za předpokladu, že na jejich detekci vybudujeme dostatečně citlivé detektory).
poznámka pro autora
Jakub Beneš,2016-06-16 17:46:18
proč si myslíte, že splynutí černých děr nelze detekovat jinak než gravitačními vlnami? jsem přesvědčen o tom, že bude vyzářeno i značné množství elektromagnetických vln. stále je to hmota a stále je s ní zacházeno dost brutálním způsobem. při splývání se s pevným horizontem událostí nedá počítat. navíc ty černé díry mohou mít kroužící hmotu ještě kolem sebe. dlouhé roky se předpokládalo, že některé gama záblesky jsou způsobeny srážkou černých děr. to už zase neplatí?
Re: poznámka pro autora
Pavel Brož,2016-06-16 20:25:56
Pokud mají černé díry ve svém okolí akreční disky z hmoty ještě nespadlé pod horizont, tak tyto disky umí generovat velice silná elektromagnetická pole i v případě, že jde o jen o jednu a nikoliv dvě černé díry. Speciálně pak např. kvazary a blazary vidíme v elektromagnetickém spektru právě proto, že ionizovaná hmota akrečních disků urychlovaná na relativistické rychlosti vysílá intenzivní záření, které se šíří nejsnadněji ve směru rotační osy (blazar se liší od kvazaru jenom úhlem jeho rotační osy vzhledem k Zemi, kdy Země se nachází prakticky ve směru nejsilnějšího vyzařování). Totéž co pro blazary a kvazary (jejichž srdcem jsou superhmotné černé díry o hmotnosti miliónů až miliard Sluncí) platí i pro černé díry hvězdných velikostí, kde samozřejmě výtrysky elmag. záření také vznikají, pouze už nejsou tak intenzivní a proto je z cizích galaxií nepozorujeme. To je ovšem ale jenom omezení dané současnými možnostmi pozorovací astronomie, ve vzdálenější budoucnosti je docela dobře myslitelné, že bude možné pozorovat i elmag. výtrysky u černých děr hvězdných velikostí. Potom samozřejmě nebude problém pozorovat ani očekávatelné zjasnění tohoto záření při splynutí dvou takových černých děr.
Pokud ale černé díry už své akreční disky "zkonzumovaly" a navíc se nenachází v oblasti zajišťující dodatečný přísun hmoty, tak při svém splynutí mohou vyzařovat významné elektromagnetické záření pouze tehdy, když je aspoň jedna z nich nabitá. Takové záření je analogické synchrotronovému záření, které vydávají nabité částice v kruhových urychlovačích - pokud by byl náboj jedné nebo obou černých děr dostatečně velký, pak by před jejich splynutím při jejich rychlém oběhu kolem sebe také docházelo k "synchrotronovému" záření, které by mohlo být pozorovatelné. Vznik černé díry disponující dostatečně velkým nábojem je ale velice nepravděpodobné.
Oproti tomu splynutí dvou NENABITÝCH černých děr BEZ akrečních disků neumožňuje vznik elektromagnetického záření vůbec - žádná hmota při tomto splynutí totiž nepřichází ke vzájemnému kontaktu, jednoduše proto, že už dávno předtím spadla pod horizont své příslušné černé díry, odkud se za velice krátký vlastní čas (v případě černých děr hvězdných velikostí se jedná o méně než milisekundu) zřítí do centrální singularity. To, co se mění při splynutí takových černých děr mění, je jenom geometrie prostoročasu (zjednodušeně řečeno ze dvou Schwarzschildových řešení popisujícího zakřivený prostoročas vznikne jedno). Tento proces podle obecné teorie relativity nenabízí žádný způsob, jak tuto měnící se prostoročasovou geometrii přeměnit na elektromagnetické záření.
Jiná situace samozřejmě nastane při srážce dvou neutronových hvězd nebo při srážce neutronové hvězdy a černé díry. V obou případech figuruje hmota, která je ještě NAD horizontem událostí (tj. hmota tvořící jednu nebo obě neutronové hvězdy). Tato hmota se během srážky bortí a vzájemně tře, přičemž samozřejmě existuje celá řada známých mechanismů, které mohou být příčinou vzniku silného elektromagnetického záření.
Re: Re: poznámka pro autora
Vojtěch Kocián,2016-06-16 22:07:44
Není možné, že by byl časoprostor a tedy i horizont událostí při splývání černých děr natolik rozvlněný, že by vygeneroval významné množství elektromagnetického Hawkingova záření?
Re: Re: Re: poznámka pro autora
Pavel Brož,2016-06-16 23:13:13
Kdepak, Hawkingovo záření tam nebude výrazně vyšší, než u původních černých děr před splynutím. Intenzita Hawkingova záření je určena velikostí slapových sil v blízkosti horizontu, a ty jsou pro volně padající hmotu (precizněji řečeno v lokální inerciální soustavě, ve které můžeme lokálně vynulovat gravitační sílu a díky tomu v ní i lokálně používat negravitační fyziku včetně kvantové teorie pole s jejími virtuálními páry částice-antičástice) v okolí horizontu tím menší, čím je černá díra větší. S trochou nadsázky se dá říct, že při průchodu horizontem černé díry o hmotnosti řádově 10 miliard Sluncí (i takové už byly v jádrech cizích galaxií objeveny) by horizontem bez úhony propadlo plato rakviček (či indiánek). Trochu matematičtěji, slapové síly jsou úměrné komponentám Riemannova tenzoru křivosti, tedy se (z důvodu jeho "tenzorovosti") na rozdíl od gravitační síly (která je úměrná složkám tzv. afinní konexe) nedají vynulovat přechodem do lokální inerciální soustavy.
Čím menší černá díra, tím větší slapové síly panují v okolí horizontu. Zjednodušeně řečeno, u gigantické černé díry o hmotnosti deseti miliard Sluncí se její horizont nachází ve vzdálenosti cca sedmkrát větší než je vzdálenost Neptuna od Slunce, pád z horizontu do centrální singularity zabere padajícímu kosmonautovi cca 4 hodiny jeho vlastního času, a během jeho průchodu horizontem se velmi velká oblast prostoru (srovnatelná minimálně s velikostí Země, s trochou tolerance i se vzdáleností Země-Měsíc) jeví jako docela plochá, tedy nezakřivená. Tzn. že předměty volně padající v takto velkém okolí kosmonauta se budou vůči sobě pohybovat s velkou přesností rovnoměrně přímočaře (stále samozřejmě používáme lokální inerciální soustavu). Nehomogenita gravitačního pole je v tomto případě tedy velmi malá, zvláště pak na škálách, na kterých se projevují kvantové fluktuace v podobě spontánního vzniku párů částice-antičástice - tedy na škálách srovnatelných s Comptonovou vlnovou délkou příslušných částic, která je např. pro elektron rovna řádově 10^-13m, a pro neutron či proton ještě o tři řády menší.
Pro miniaturní černou díru už je situace jiná - černá díra o hmotnosti řádově miliardy tun už má Schwarzschildův poloměr řádově srovnatelný s Comptonovou vlnovou délkou protonu, a proto v blízkosti jejího horizontu budou vliv nehomogenit gravitačního pole na spontánně vznikající páry částice-antičástice docela podstatný, a bude se projevovat právě explozivně se zrychlujícím Hawkingovým vypařováním.
Při splynutí černých děr se očekává (a z teorie také plyne) vznik gravitačních vln o vlnových délkách řádově blízkých k rozměrům výsledné černé díry. Abychom dostali výraznější produkci Hawkingova záření, musely by opět masivně vznikat gravitační vlny o vlnové délce blízké ke Comptonově vlnové délce částic Hawkingova záření. Tak krátkovlnné gravitační vlny ale při srážkách černých děr hvězdných velikostí nemají šanci vzniknout.
Re: Re: Re: Re: poznámka pro autora
Vojtěch Kocián,2016-06-17 07:09:13
Děkuji za vyčerpávající odpověď.
Děkuji za přesné trefy do středu černé
Josef Hrncirik,2016-06-17 08:55:14
Mám jen 3 triviální dotazy.
a) Pokud zde splynutí vyzářilo Mo, kolik % z toho připadá na poslední oběh před žbluňkem (vrcholem)?
b) Kolik procent původního momentu hybnosti (z cca 1 h před žbluňkem) přejde do rotace po splynutí?
c) Min. ?. max. frekvence otáček před a po žbluňku?
Díky i za kvalifikované odhady.
Re: Děkuji za přesné trefy do středu černé
,2016-06-17 08:58:40
a) Ne víc než tři a třicet.
b) 100%
c) Před 0,1 při limitě a po zatnutí zubů.
Mohlo by být.
Re: Re: Děkuji za přesné trefy do středu černé
Josef Hrncirik,2016-06-17 10:35:01
a) ano, ale míníte + či AND?
Určitě to ale inkontinentuje vlny dosti dlouho, takže na závěr je asi v nádrži podstatně méně než 3%
b) vlny jsou energie a tudíž hmota; Tento ether je asi strháván ve směru rotace.
Rotací eteru se brzdí rotace díry. Nebylo by to 10%?
c) Záleží na pořadí?
Re: Re: Re: Děkuji za přesné trefy do středu černé
Pavel Brož,2016-06-18 00:02:36
Zkusím Vám nabídnout jiné odpovědi, než jste dostal od neznámého komentátora výše:
a) z obrázků lze zhruba odhadnout, že během oněch pozorovaných 27 oběhů vzrostla amplituda vln zhruba čtyřikrát. Pokud bychom hrubě extrapolovali tento vývoj do doby dvě sekundy před splynutím (místo pozorované jedné sekundy), tak za ty poslední dvě sekundy by ta amplituda vln vzrostla 16 krát. Pokud zanedbáme energii vyzářenou ještě dříve než před dvěmi sekundami před splynutím, tak potom lze učinit jakousi mlhavou intuitivní představu
b) méně než 100 procent, protože část impulsmomentu odnesou gravitační vlny
c) z obrázků lze napočítat něco přes padesát period, ty mají korespondovat s údajnými 27 oběhy, tedy pravděpodobně dvě periody připadají na jeden oběh. V článku je pak zmíněna maximální frekvence 450 Hz, tudíž maximální frekvence oběhu by měla být poloviční, tj. cca 225 Hz.
Netvrdím, že musím mít pravdu já a neznámý komentátor výše ji nemá, prostě si vyberte.
Šíření informace v gravitačním poli
Miko Landa,2016-06-16 15:41:01
Podle Obecné teorie relativity je rychlost šíření světla (obecně informace) ve vakuu vždy stejná. To musí platit i v prostoru kde je sice vakuum ale různé gravitační pole. Potom se mnění prostoročas. Změním-li vzdálenost, změní se čas – relativní rychlost světla se samozřejmě nemění (viz opravy GPS). Zajímalo by mě, proč se tvůrci detektoru LIGO tváří, že se jich to netýká. Vždyť při průchodu gravitační vlny se nejen změní relativní vzdálenost zrcadel (rozměr ramen detektoru) ale změní se i gravitační pole a s ním i prostoročas – změní se tedy i rozměr „metru“ (měřidla). Nikde jsem dosud nezaznamenal rozbor této problematiky. Nechcete se o to pokusit pane Wagnere? Předem díky.
Re: Šíření informace v gravitačním poli
Pulec Plavčík,2016-06-16 16:39:19
To je relativita relativity, nechápu, co Vám na tom příjde divné nebo nepochopitelné. Měli by Vás zablokovat.
Re: Šíření informace v gravitačním poli
Richard Palkovac,2016-06-16 18:58:48
Rozmyslate ako pan Lorentz, ked chcel napasovat matematiku tak (Lorentzove transformacie) aby zachranil teoriu eteru po MMX experimente. Neuvedomil si ale (rovnako ako vsetci ostatni az po pana Einsteina) ze tym by vlastne zrusil fyziku. Ved ako by sme mohli popisat fyzikalne deje, ak by mal byt nas "meter" raz kratsi a raz dlhsi ?
Na spravnu mieru to dal az pan Einstein, ktory pochopil, ze ak chcete deje popisovat fyzikalne, tak musi fyzika platit rovnako pre vsetkych. Dlzka nasho "metra" sa nikdy nemeni, ona absolutne vlastne ani nedava zmysel, zmysel dava len pomer, dlzka nasho "metra" k dlzke "metra" niekoho ineho a to je relativita.
Co sa tyka GPS, tak tomu v podstate moze byt relativita ukradnuta, popisuje to tu :
http://riki1.eu/Preco_GPS_funguje.htm
Re: Šíření informace v gravitačním poli
Pavel Brož,2016-06-17 00:10:49
Jenom ve zkratce, protože není mým cílem nabídnout rychlokurz ani speciální, ani obecné teorie relativity.
Takže: ve speciální teorii relativity je rychlost světla ve všech INERCIÁLNÍCH soustavách stejná. Toto tvrzení může začít dávat nějaký smysl pouze když řekneme, co jsou to inerciální soustavy, či jak je poznáme. Inerciální soustavy poznáme tak, že v nich pro volně levitující nenabitá tělesa platí první Newtonův zákon, tj. že se vůči sobě pohybují rovnoměrně přímočaře. pokud jednu takovou soustavu najdeme, a pokud přejdeme do nové soustavy pohybující se vůči té první rovnoměrně přímočaře, tak nová soustava bude také inerciální, protože i v ní bude pro prve sledovaná tělesa platit první Newtonův zákon. Naopak pokud přejdeme do soustavy rotující, tak zjistíme, že v ní pro sledovaná volně levitující tělesa první Newtonův zákon neplatí, protože se vůči nám budou obecně periodicky zrychlovat a zpomalovat.
Speciální relativita je formulována převážně v inerciálních soustavách. Do neinerciálních soustav se samozřejmě dá vždycky přeformulovat, tak jako je to možné i v Newtonovské fyzice, spousta tvrzení už ale v neinerciálních soustavách neplatí (nejde o nic nepochopitelného, v Newtonovské fyzice je tomu analogicky). Tak např. samotné světlo se v neinerciální soustavě nepohybuje rovnoměrně přímočaře - v rovnoměrně se zrychlující kabině opíše světelný paprsek místo přímky parabolickou dráhu, a opět, jedná se o banální geometrii, není na tom nic záhadného.
Speciální teorie relativity nezahrnovala gravitaci. Tu se podařilo konzistentně zahrnout rozšířením této teorie do tzv. obecné teorie relativity. Obecná teorie relativity přibrala ke speciální teorii relativity axiom o lokální ekvivalenci zrychlení a gravitačního působení. Tento axiom je experimentálně velice precizně ověřený a stále ověřovaný, protože s jeho pádem by padla i obecná teorie relativity. Tento axiom říká, že gravitační pole lze lokálně "vyvolat" přechodem do zrychlené soustavy, či naopak lokálně "anulovat" přechodem do volně padající soustavy. Díky tomu se spousta "práce" v popisu gravitačních jevů podle obecné teorie relativity zjednodušila, protože lokálně si díky přijatým axiomům můžeme gravitaci "vypnout" (ovšem jen v dostatečně malém okolí zkoumaného jevu) přechodem do volně padající soustavy, čímž pádem se vracíme speciální teorie relativity, kterou už známe. Tzn. že opět můžeme pracovat s inerciálními soustavami úplně stejně, jako ve speciální teorii relativity, nyní ovšem s důležitým adjektivem: LOKÁLNÍ inerciální soustava. Lokální je proto, že gravitaci lze vynulovat pouze lokálně, nikoliv globálně. Tzn. že pokud padáte v gravitačním poli Země směrem k jejímu středu, tak tělesa k vám dostatečně blízká se vůči vám budou v lokální inerciální soustavě pohybovat s velkou přesností rovnoměrně přímočaře. Pokud ale pozorovací oblast rozšíříte tak, aby zahrnovala i druhého laboranta padajícího z druhé strany Země k jejímu středu, tak zjistíte, že ten se vůči vám nebude pohybovat rovnoměrně přímočaře ani náhodou - bude se totiž vůči vám pohybovat se zrychlením 2 g (dvojka je tam proto, že to své vlastní g jste "vyrušili" popisem v soustavě volně padající spolu s vámi).
Takže díky postulované ekvivalenci mezi lokálním gravitačním polem a zrychlením může obecná teorie relativity bez problémů používat pojmy a tvrzení převzaté ze speciální teorie relativity, pokud ovšem zdůrazníme, že se platnost těchto tvrzení je lokální a že pracujeme v lokálních inerciálních soustavách. Např. tak dostaneme i zmiňovanou konstantnost rychlosti šíření světla - musíme ale dodat, že toto tvrzení platí lokálně a pokud pracujeme v lokální inerciální soustavě.
Ukažme si příklad, kdy zmíněné tvrzení neplatí. Dejme tomu, že máme možnost vyslat světelný paprsek ke dvěma vůči nám astronomicky vzdáleným protilehlým zrcadlům, která jsou vůči nám stejně daleko. Změříme dobu, za jakou se k nám vrátí odražené paprsky, čímž ověříme stejnou vzdálenost zrcadel od nás. Pak si počkáme, až jednou se do cesty jednoho z nich přiblíží hmotná hvězda. Tento paprsek se jednak ohne v důsledku průchodu jejím gravitačním polem, a jednak zpomalí, takže odražený paprsek k nám dojde později, než paprsek vyslaný k zrcadlu na opačné straně od nás. Takže jak potom můžeme tvrdit, že rychlost šíření světla ve vakuu je vždy stejná, když je ve druhém případě prokazatelně nižší, než v prvém?
Toto je ukázka toho, k jakým nejasnostem a zmatením běžně dochází, pokud se pečlivě neřekne, v jakých soustavách svá tvrzení formulujeme. Např. v druhém případu s ohybem paprsku kolem hvězdy se dá ukázat, že jsme nepracovali v lokální inerciální soustavě, ale v sice globální, ale zato neinerciální soustavě. Ta neinerciálnost se pozná např. podle toho, že na popisovaných vzdálenostech neplatí pro volně levitující tělesa první Newtonův zákon (opravdu ne, pokud totiž hmotnost tranzitující hvězdy je dostatečná pro ohyb světelného paprsku, tak volně levitující tělesa se v jejím okolí opravdu nebudou pohybovat podle prvního Newtonova zákona).
Suma sumárum: tvrzení, že podle obecné teorie relativity je rychlost šíření světla ve vakuu vždy konstantní, je tvrzení nepravdivé. Pravdivé je až tvrzení, že podle obecné teorie relativity je rychlost šíření světla měřená lokálně a v lokální inerciální soustavě vždy konstantní. Ta přidaná upřesnění jsou tam zcela zásadní.
Re: Re: Šíření informace v gravitačním poli
Richard Palkovac,2016-06-17 10:18:15
Procesy v silnejsom gravitacnom poli, ak ich pozorujeme zo slabsieho gravitacneho pola, sa spomalia, cize aj to svetlo ktore leti v silnejsom grav.poli a pozorujeme ho zo slabsieho grav.pola sa pre nas spomaluje. Je to logicke, kedze svetlo tie vsetky procesy vlastne sprostredkuje interakciou fotonov.
Ale co efekt gravitacneho praku, ktory vo vasom myslienkovom experimente urcite tiez posobi ?
Zvisi sa frekvencia toho svetla (ziska vacsiu energiu), ked prejde okolo hviezdy ? Lebo jeho rychlost sa zvysovat predpokladam nemoze.
Re: Re: Re: Šíření informace v gravitačním poli
Pavel Brož,2016-06-17 23:31:16
Neberte to zle, ale podobně jako pan Miko Landa používáte nepřesné formulace, tím pádem pravdivost Vašich tvrzení záleží na dodatečných zpřesněních. Jedná se konkrétně o tvrzení, že procesy v gravitačním poli se zpomalují, pokud je pozorujeme ze slabšího gravitačního pole. Pokud pro konkrétnost vezmeme prostoročas křivený statickou sféricky symetricky rozloženou hmotou, tak ve statické soustavě opravdu zjistíme, že v místech se silnějším gravitačním polem (přesněji řečeno v místech blíže k centrální hmotě) probíhají procesy pomaleji než v místech se slabším gravitačním polem (přesněji řečeno v místech dále od centrální hmoty). Můžeme ale pracovat i v nestatických soustavách. Jedna z nich je např. soustava volně padající. V této soustavě během pádu zjistíme, že procesy probíhají úplně stejně rychle bez ohledu na vzdálenost od centra hmoty. Můžeme ale také pracovat v soustavě pevně spojené s rychle se točícím kolotočem (střed kolotoče nemusí být totožný s centrem hmoty). Potom při dostatečné rychlosti rotace kolotoče zjistíme, že procesy na něm naopak probíhají pomaleji než procesy blíže k centru hmoty.
Zkrátka a dobře záleží na přesné definici toho, co a jak vlastně měříme a v jaké soustavě. Pokud necháme jedny atomové hodiny obíhat na orbitě Země a jiné na nižší, pak ty na nižší dráze se budou proti těm na vyšší zpožďovat. Je přitom jedno, jestli je porovnáváme pomocí světelných signálů anebo jestli je po dostatečně dlouhé době navedeme na tutéž dráhu a porovnáme. Pokud ale ty na vyšší dráze dáme do dostatečně rychlé centrifugy, pak to dopadne přesně opačně. Zmiňuji to proto, že píšete, že zpomalování procesů v silnějším gravitačním poli je logické jelikož světlo tyto procesy zprostředkuje interakcí fotonů. V příkladu výše se ukazuje, že naopak procesy v slabším gravitačním poli mohou za jistých okolností probíhat pomaleji než v tom silnějším, a je přitom úplně jedno, jestli jsou tyto procesy zprostředkovány fotony nebo jinak.
Co se týče Vaší otázky ohledně zvýšení energie světla efektem gravitačního praku. Ano, opravdu dojde k nepatrné změně finální frekvence v důsledku příčného Dopplerova efektu - příčného proto, že předpokládáme, že odchylka paprsku je malá. V důsledku příčného Dopplerova efektu se frekvence světla změní v řádu (v/c)^2, kde v je rychlost tranzitující hvězdy. V okamžiku průchodu paprsku kolem hvězdy se ale jeho frekvence změní v řádu delta_chi/(c^2), kde delta_chi je rozdíl gravitačního potenciálu v místech největší a nejmenší vzdálenosti fotonu od tranzitující hvězdy. Měl jsem tedy zvolit sofistikovanější případ, při kterém by nedošlo k ohybu paprsku a tím pádem ani k dodatečnému příčnému Dopplerovu jevu, a tím pádem by jednoznačně zbyl jen vliv gravitačního potenciálu. Takže předpokládejme, že ten paprsek prochází na své pouti symetricky mezi dvěma stejně velkými hvězdami. Tzn. z levé i pravé strany na něj působí stejná gravitační síla, k žádnému ohybu, tím pádem ani k žádnému efektu gravitačního praku a tím pádem ani k žádnému příčnému Dopplerovu jevu nedojde, a zbude jen vliv toho rozdílu gravitačního potenciálu. Ke zpoždění příchodu paprsku i v tomto případě dojde.
Re: Re: Re: Re: Šíření informace v gravitačním poli
Richard Palkovac,2016-06-18 09:05:08
Dakujem Vam za vycerpavajucu a perfektnu odpoved (ako vzdy).
Mne je jasne, ze podla OTR je gravitacia a zrychlenie to iste. Takze ak volne padate, tak v kazdom momente padate takym zrychlenim v akom silnom gravitacnom poli sa nachadzate a preto to zrychlenie presne anuluje vplyv gravitacie, cize aspon v blizkom okoli konkretneho bodu ste v inercialnej sustave.(problem je, ze zrychlenie ma jeden konkretny smer a gravitacne silove posobenie ma ten isty smer len v jednom bode, priamke, v jeho okoli sa uz ten smer meni) Rovnako je to aj s kolotocmi, tie ked rozkrutite dostatocne rychlo, tak akceleracny potencial moze prekonat gravitacny potencial a zrazu pomer casov dvoch pozorvatelov moze byt opacny ako bol pred rozkrutenim kolotoca.
Vzdy ale ide o relativitu, teda len o pomer dvoch casov. Povedat , ze v konkretnom bode priestoru bezi cas rychlostou "xy" nedava zmysel, aj ked sa nam zda ze ano, lebo stale sme myslienkami spojeny s nasou Zemou.
Tento prispevok nepisem preto, aby som Vas nieco nove "naucil" , ale preto, aby ste ma pripadne opravil, ak som nieco napisal zle, vopred dakujem.
Re: Re: Re: Re: Re: Šíření informace v gravitačním poli
Richard Palkovac,2016-06-18 09:34:49
To, ze zrychlenie "anuluje" gravitaciu, som mal v zmysle vplyvu na rychlost behu casu.
Re: Re: Re: Re: Re: Re: Šíření informace v gravitačním poli
Pavel Brož,2016-06-18 12:32:51
To je v pořádku, píšete to správně. Naopak já se omlouvám za svou obsesi vyžadující přesné formulace. Ono je to v případě obecné teorie relativity opravdu složitější, než v teoriích negravitačních polí, právě proto že gravitace je v OTR "geometrizována", tj. dá se např. lokálně odrušit přechodem do lokální inerciální soustavy, či naopak lokálně vyvolat přechodem do soustavy zrychlené. Globálně to naopak nejde, nelze např. vytvořit takovou globální byť různě se deformující soustavu, která by v plochém prostoročase globálně nasimulovala např. gravitační pole Země. Taktéž slapové síly se dají rozpoznat jakožto projevy "skutečné" gravitace, nikoliv jen jakožto projev vyvolaný volbou soustavy. Tak např. to, že tyto síly způsobují vulkanickou či kryovulkanickou činnost na Jupiterových měsících je fyzikální fakt, který nejde "odtransformovat" volbou soustavy.
Z toho důvodu je kolikrát zrádné používat v souvislosti s konkrétními procesy název gravitace. Fyzici upřednostňují termíny jako jsou metrický tenzor, afinní konexe, Riemannův tenzor. Metrický tenzor určuje souřadnicové délky a souřadnicový čas, ale také i úhly mezi jednotlivými souřadnicovými osami v tom kterém bodě, a také vzdálenosti mezi dvěma body vyjádřené ve zvolených souřadnicích. Můžeme si ho představit jako čtyřrozměrnou analogii volby zeměpisných souřadnic - tam taky můžeme používat kromě obvyklých zeměpisných délek a šířek i všemožné jiné souřadnice. Změnou těchto souřadnic se samozřejmě geometrie zemského povrchu nezmění, ale např. ty vzdálenosti mezi dvěma body se bodou počítat v nových souřadnicích jinak, než v těch starých. A podobně jako u Země umíme lokálně zavést téměř pravoúhlou souřadnicovou síť (globálně se nám to ale nepovede), tak u metrického tenzoru v prostoročasu umíme lokálně zavést Minkowského prostoročasové souřadnice známé ze speciální teorii relativity.
Afinní konexe určuje pro změnu gravitační zrychlení, jaké má těleso v daném metrickém poli. Afinní konexe se počítá z metrického tenzoru, takže zadáme-li globálně metrický tenzor, známe globálně i afinní konexi. Afinní konexe se dá lokálně vynulovat přechodem do padající soustavy, globálně to opět jako u metrického tenzoru v obecném metrickém poli nejde.
Riemannův tenzor určuje ty "skutečné" gravitační síly, např. ty slapové. Právě tento tenzor mimochodem určuje oscilace ramen detektoru aLIGO při průchodu gravitační vlny. Počítá se z afinní konexe. Pokud je prostoročas v některé soustavě globálně plochý, je Riemannův tenzor nulový ve všech bodech a ve všech soustavách, nejen v té výchozí. A platí to i naopak, pokud je v nějakém bodě a v nějaké zvolené soustavě nenulový, je v tomto bodě nenulový už ve všech soustavách. Tzn. že na rozdíl od afinní konexe ho nelze lokálně vynulovat přechodem do nějaké speciální soustavy. Složky Riemannova tenzoru určují křivost prostoročasu. Je-li prostoročas zakřivený, pak tím pádem neexistuje žádný globální systém, ve kterém by se metrický tenzor jevil stejně, jako ve speciální relativitě, a ve kterém by tím pádem i ve všech bodech vymizela afinní konexe - je to situace analogická, jako když se na zemském povrchu nedá zavést globálně kartézský systém.
Každá z těchto veličin - metrický tenzor, afinní konexe a Riemannův tenzor - popisuje jiné aspekty fyzikálních procesů probíhajících v prostoročase. Právě proto lze dojít k nejednoznačnostem při použití společného termínu gravitace pro tyto různé aspekty. Pouze na toto jsem chtěl poukázat.
Zajímavé
Alexandr Kostka,2016-06-16 12:31:31
Pozorování rozhodně zajímavé, ale trochu mi k tomu nesedí ta četnost záchytů. 3 události za půl roku? 6 do roka? Pokud jsou černé díry tak běžné, že se srážejí několikrát ročně, tak jak vůbec může existovat nějaká hmota nepohlcená další černou dírou?
Re: Zajímavé
Drahomír Strouhal,2016-06-16 12:44:27
Bavíme se o malých černých dírách v prostoru 3 miliard světelných let, kde jsou desetitisíce galaxií a v nich hmota miliardnásobků hmotnosti oněch srážek. 6 srážek za rok? Docela málo... Je jich určitě víc, jenom je nejsme schopní detekovat.
Re: Re: Zajímavé
Jiří Svejkovský,2016-06-16 12:47:56
Vlny musí přijít ze správného směru. To zužuje "zorné pole" detektoru na malou část oblohy.
Re: Re: Re: Zajímavé
Drahomír Strouhal,2016-06-16 12:56:42
To jste si špatně vyložil. Vlny mohou přijít z jakéhokoli směru, ale s rostoucí odchylkou od dvou ideálních os (detektor je složený ze dvou k sobě kolmých zařízení) se jeho účinnost detekce snižuje. V kolmici potom je neschopen měřit. Ta část oblohy, která je hůře měřitelná, je výřez dvou kuželů kolem kolmice k detektoru.
Takže to rozhodně není malá část oblohy.
Je to trochu divné
Drahomír Strouhal,2016-06-16 12:27:15
Zdá se mi to, nebo uvolněná energie je vždy přibližně 1/21,5 celkové původní hmotnosti černých děr? Existuje na to nějaký zákon? Jaktože je zlomek uvolněné energie stejný i v případě různé vzájemné velikosti černých děr? Výsledek byl totiž přibližně stejný jak v poměru hmotností 1:2, tak v poměru 1:1,24.
Přijde mi to divné.
Ako rozlisit ...
Richard Palkovac,2016-06-16 09:01:44
Ako sa da rozlisit takymto pristrojom, na taku vzdialenost, ci doslo k splynutiu dvoch ciernych dier, alebo k splynutiu dvoch hviezd podobnych hmotnosti ? Viem , ze prakticky je meranie sporne, kedze sum je priblizne na urovni meraneho signalu.
Predpoklada sa, ze hviezdy by sa pri zrazke rozpadli (nesplynuli) a cierne diery ano ?
Re: Ako rozlisit ...
Martin Krupicka,2016-06-16 10:32:52
Laicky bych tipl, ze splynuti cehokoli jineho nez cernych der se projevi i v elektromagnetickem poli jako napr. supernova.
Re: Ako rozlisit ...
Vojtěch Kocián,2016-06-16 11:09:47
Cokoliv jiného než černé díry má při dané hmotnosti příliš velký průměr na to, aby to kolem sebe mohlo obíhat tak rychle. Kdyby to byly hvězdy, splynuly by (a signál by se vytratil) už při mnohem nižších frekvencích. Efekt v elektromagnetickém spektru je asi možný ať už jde o černé díry nebo cokoliv jiného. Jen se na takovou vzdálenost a s nepřesností LIGO při určování směru nedá rozumně identifikovat.
Re: Re: Ako rozlisit ...
Jiří Svejkovský,2016-06-16 11:18:26
Pokud jsem to správně pochopil, nedetekovaly se vlny elektromagnetické, nýbrž gravitační. Vtom je krapet rozdíl.
Re: Re: Re: Ako rozlisit ...
Vojtěch Kocián,2016-06-16 12:16:58
Ano. Jen jsem psal, že dohledat k dané události i projev v oboru elektromagnetických vln, je za současného stavu prakticky nemožné. Až bude dostatečně citlivých gravitačních detektorů dost, bude možné událost zaměřit a nasměrovat na to místo i optické (rádiové, rentgenové, gamma...) teleskopy a podívat se, jak vypadá výsledek. Srážku extrémně hmotných objektů by teoreticky mělo jít i předpovědět a podívat se na ni v elektromagnetickém oboru naživo. Zřejmě nás čeká zajímavé období.
Re: Re: Re: Re: Ako rozlisit ...
Richard Palkovac,2016-06-16 12:45:55
Diky za vysvetlenie, mohol som si to domysliet, ale som si pozorne neprecital clanok a neuvedomil som si, ze ide vlastne o zachytenie gravitacnych vln, ktore vyprodukuju posledne extremne rychle otocky dvoch ciernych dier okolo spolocneho taziska. Myslel som, nespravne, ze tie grav. vlny su vyprodukovane aktom spojenia.
šum
Blu .,2016-06-16 08:29:52
v signále ktorý je vlastne odfiltrovaný šum, hľadajú vedci modulovaný šum ktorý je rádovo 10-22 menší. používajú na to matematické algoritmy štatistickej fyziky a grid-computing. Je to stále len nepriame meranie niečoho čo si myslia že existuje v nejakej teórii.
V podstate aj môj merateľný ranný únik ritných plynov spôsobuje malé štatistické odchýlky gravitačného vlnenia oboch "polovičiek" môjho sedacie svalu. Tiež sa z toho teším ... len neviem čo to dokazuje.
Pekný deň priatelia
:o)
Re: šum
Viliam Mlich,2016-06-16 09:49:26
Pokiaľ na to chvenie polovičiek spotrebujete energiu hmotnosti slnka, tak to prístroje určite od šumu rozpoznajú.
Pokud s tím intereagují více než s např. s neutriny
Josef Hrncirik,2016-06-16 11:21:43
tj. mají dostatečný ztrátový úhel
Jak vidno zříti z grafů S/N Monte Carlo technologie věštby z kávové sedliny umožňuje nejen predikovat i bez žetonů, kdy padne sudá, ale hlavně kdy padne 32
Josef Hrncirik,2016-06-17 08:38:34
,2016-06-16 08:27:11
Prostor se vůči gravitační vlně chová jako newtonovská tekutina, takže to budou asi nějaké šumy. Fyzika získá nový přídomek - šumná.
Vendelin Omacka,2016-06-16 07:32:29
26. prosince 2016? :) asi to chcelo byt 2015
Ale nebudem len rypat. Viacero zaujimavych ulovkov urcite zvysi motivaciu pre financovanie projektu eLISA, hlavne ak sa teraz potvrdilo, ze jeden z milnikov je zvladnuty takmer radovo lepsie, ako sa ocakavalo.
Škoda, že je to dost z ruky
Jiří Svejkovský,2016-06-16 07:09:03
To musel bejt mazec. Jak asi dopadlo přímé okolí? To asi nebyly vlnky 10 na-22.
Makrovlnný ohřev. Oč se ohřeje kosmonaut, který si na 0,4 s sundá antigravitační vestu při strainu 10**-4 a 125 Hz, tj. ve vzdálenosti 1,4 klr od makrovlnky cca 0,5 s před zkratem?
Josef Hrncirik,2016-06-16 08:45:27
Jaký má ztrátový úhel?
Re: Makrovlnný ohřev. Oč se ohřeje kosmonaut, který si na 0,4 s sundá antigravitační vestu při strainu 10**-4 a 125 Hz, tj. ve vzdálenosti 1,4 klr od makrovlnky cca 0,5 s před zkratem?
Jiří Svejkovský,2016-06-16 10:48:44
Ehm, cožeto?
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce