Když jsem před deseti lety psal podrobný článek o vlastnostech neutrina a historii jeho zkoumání, bylo budování experimentu KATRIN (KArlsruhe TRItium Neutrino experiment) na svém počátku. I když vakuová komora spektrometru o průměru deset metrů už absolvovala svou vodní cestu kolem celé Evropy. V minulém roce se zařízení, které velice přesně měří energie elektronů emitovaných v rozpadu tritia, podařilo konečně dokončit.
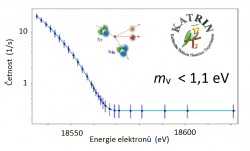
Naměřené spektrum elektronů v sobě nese informaci o hmotnosti neutrina. Při beta rozpadu tritia vzniknou celkově tři objekty, prvním je helium 3, druhým pak elektron a třetím antineutrinu. Ty si mezi sebou rozdělí energii, která se při rozpadu uvolní. Na neutrino nemůže zůstat méně energie, než je obsaženo v jeho klidové hmotnosti. Tím je ovlivněna i koncová část spektra emitovaných elektronů. Tritium je velmi vhodné pro určování hmotnosti pomocí jeho rozpadu. Energie, která se uvolňuje při jeho beta rozpadu, je totiž jednou z nejmenších, pouze necelých 19 keV. Připomeňme, že klidová energie elektronu, což je druhá nejlehčí známá částice, je 511 keV. Právě u tohoto rozpadu je tak největší šance vidět vliv extrémně malé klidové energie související s klidovou hmotností na spektrum elektronů.
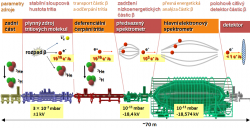
Spektrometr je postaven tak, že dokáže zkoumat rozpad plynného tritia. Tím se vyloučí vliv vazby atomů tritia v pevném terči, který byl pozorován v předchozích experimentech. Jejich energie už je srovnatelná s klidovou energií neutrina. Celá sestava spektrometru je dlouhá okolo 70m. Ze všech elektronů vyzářených při rozpadech tritia se vyseparují ty z nejvyšší energií. Ty se pak pošlou do hlavního spektrometru, kde se přesně určí jejich energie. Jejich detekci po průchodu spektrometrem zajišťuje systém 148 detektorů.
Elektrostatický spektrometr funguje tak, že se postupně zvyšuje napětí, které zadržuje elektrony se stále vyšší energií. Jde tak o jednokanálové měření, kdy při jednotlivém daném měření zjišťujeme, kolik elektronů má energii vyšší, než je nutná pro překonání hradby nastaveného napětí. Samotné spektrum se pak získá tak, že se odečtou naměřené počty elektronů v sousedních kanálech. Měření je velmi citlivé k přesnosti nastavení a stability napětí na spektrometru. Ta musí dosáhnout hodnoty ppm, tedy miliontiny jmenovitého napětí 18,6 kV.
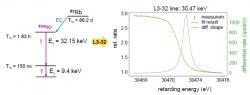
Danou přesnost měření stability nelze dosáhnout žádnými elektronickými přístroji. Proto se stabilita kontroluje pomocí zdroje vyzařujícího konverzní elektrony s přesně definovanou jedinou energií. Využívá se plynový zdroj těchto konverzích elektronů založený na vybuzeném stavu kryptonu 83mKr s delší dobou života (izomerním stavu). Při jeho deexcitaci se emitují potřebné konverzní elektrony. Tento radionuklid má však krátký poločas rozpadu. Proto se produkuje radionuklidový zdroj 83Rb, který se na něj rozpadá a jehož poločas rozpadu je 86 dní. A právě metodika takové energetické kalibrace a monitorování spektrometru se vypracovala v Ústavu jaderné fyziky AV ČR v Řeži českou částí spolupráce KATRIN. Zde se také pomocí zdejšího cyklotronu produkuje i potřebný radionuklid rubidia.
Podrobně o dokončení spektrometru KATRIN v minulém roce povídal v rozhovoru pro Osla Otokar Dragoun, který je jednou z klíčových osobností české části spolupráce KATRIN. Ten také podrobně rozebíral rozvoj elektronové spektrometrie v Ústavu jaderné fyziky, českou cestu k experimentu KATRIN a jak se spektrometr podařilo vybudovat. Délka jeho konstrukce je dána i tím, že jde o zařízení pracující na současných technologických limitech. I díky tomu však vzniká jeho velký přínos pro pokrok vědy i technologie v oboru.
V první polovině roku se uskutečnila první měření na novém spektrometru s plynným tritiem, která trvala zhruba čtyři týdny. Analýzu získaného spektra prováděly tři nezávislé skupiny. Rozbor koncové části elektronového spektra je totiž velmi náročnou záležitostí a bylo třeba vyloučit možnost chyby v analýze. Ukázalo se, že všechna tři nezávislá zpracování dosáhla shodných výsledků. Ukázala, že na úrovní 90 % pravděpodobnosti je klidová energie neutrina nižší než 1 eV. Již za tak krátkou dobu se podařilo snížit hodnotu horní limity více než dvakrát oproti předchozím nejlepším experimentům, které proběhly v německém Heidelbergu a ruském Troicku. Zároveň je tato hodnota půlmilionkrát nižší, než je klidová energie druhé nejlehčí známé částice elektronu.
Ukazuje se tak extrémně velký potenciál, který zařízení má. Je vysoce pravděpodobné, že se předpokládané dosažení limity na úrovni 0,2 eV během prvních pár let měření podaří. Reliktní neutrina jsou po reliktních fotonech nejpočetnější částicí ve vesmíru. Znalost jejích hmotnosti je tak velmi důležitou informací pro modely vývoje našeho vesmíru.
Zároveň je třeba připomenout, že kromě elektronového neutrina (a antineutrina), které doprovázejí rozpad beta, existují ještě další dva typy. Právě jev oscilací mezi různými typy neutrin, při kterém dochází k přeměně jednoho typu neutrina na druhé, je důkazem, že alespoň dva typy těchto částic musí mít nenulovou klidovou hmotnost. Za prokázání tohoto jevu dostali v roce 2015 Nobelovu cenu za fyziku Takaaki Kadžita a Arthur B McDonald. Svými exotickými vlastnostmi by neutrina mohla být oknem do hájenství nové fyziky za Standardním modelem částic a interakcí. Podrobněji jsem vlastnosti neutrin rozebral v cyklu článků (zde, zde, zde a zde). Další informace o studiu oscilací jsou zde, zde a zde.
Právě studium oscilací a určení hmotnosti neutrin by se tak mohlo stát zdrojem informací o nové exotické fyzice. Je tak excelentní, že dlouhá výstavba a příprava spektrometru byla úspěšná a zařízení se pustilo do práce. Můžeme se tak těšit, že v následujících dvou letech se naše poznání této částice i díky experimentu KATRIN posune významně dopředu. Na stránkách AV ČR a Ústavu jaderné fyziky AV ČR lze nalézt českou verzi tiskové zprávy experimentu KATRIN a výsledky měření a analýzy pro odborníky jsou v článku na arXiv zde a zde.
Diskuze:
Já taky děkuji a jako laik jsem pochopil mnohé
Karel Ralský,2019-09-27 13:54:09
aspekty, díky zdejším diskuzním příspěvkům odborníků na tuto problematiku a napadla mě v tomto kontextu že hmota se skládá, podobně jako rybí časové šupiny a poměrně "jednoduchým" způsobem složené. Ale k Plankovi to má ještě daleko, tak je možné že budeme hmotu ještě víc dělit a například Higsův boson se rozdělí na více částí, v rámci energetického spektra, podobně jako osciluje neutrino nebo kvarky se svými vůněmi.
Platí, že
Vladimír Bzdušek,2019-09-17 16:56:40
kvôli nenulovej hmotnosti neutrína sa ono nemôže pohybovať rýchlosťou svetla?
Re: Platí, že
Pavel Brož,2019-09-17 19:07:15
Ano, platí. Nicméně protože neutrina vytvářená v běžných procesech typu beta rozpad anebo v různých jaderných reakcích nebo srážkách částic mají energii typicky o dvanáct i více řádů větší, než je jejich klidová energie, tak je jejich rychlost tak hodně blízká rychlosti světla, že ji od ní v současné době neumíme rozlišit. Dokonce neutrina vzniklá při explozi i milióny světelných let vzdálené supernovy tady budou naopak o maličko dříve, než fotony, protože ty se na rozdíl od neutrin maličko zdrží při prokousávání se odmršťovanými obálkami umírající hvězdy, zatímco neutrina, ač o zanedbatelnou částku pomalejší než fotony, těmito obálkami projdou jak horký nůž máslem. Výrazně pomalejší než světlo mají být pouze reliktní neutrina, tedy ta vzniklá v době, kdy se stáří vesmíru měřilo řádově ve vteřinách až minutách - tato neutrina ale dnes ještě neumíme detekovat, a osobně pochybuji o tom, že do konce tohoto století budeme umět.
Re: Re: Platí, že
Pavel Brož,2019-09-17 23:06:52
Oops, omlouvám se - uspěchal jsem se v těch řádech - typická produkovaná neutrina mají energie v řádu MeV a vyšší, tedy o šest i více řádů větší než jejich klidová energie. Rozdíl jejich rychlostí od rychlosti světla je o dvanáct či více řádů menší, než je rychlost světla, tady ta dvanáctka vznikla. Pokud má neutrino klidovou energii 1 eV a celkovou energii 1 MeV, tak se jeho rychlost liší od rychlosti světla o pouhých 0,5*10^-12 c, tedy o pouhých 0,15 milimetrů za sekundu. Nicméně registrují se i neutrina o energiích řádově i TeV až PeV, tedy i o dvanáct až patnáct řádů vyšších, než je jejich klidová energie - toto ale nejsou typické energie neutrin vznikajících v beta rozpadech, jaderných reakcích, event. vznikajících při explozích supernov, tam jsou typické ty energie v řádech MeV a výše.
Ďakujem za odpoveď,
Vladimír Bzdušek,2019-09-18 07:55:54
a len zo zvedavosti ešte otázka. Ak teda neutríno má kľudovú hmotnosť, dokázalo by sa "zastaviť" na nulovú rýchlosť?
Re: Ďakujem za odpoveď,
Pavel Brož,2019-09-18 10:37:18
Ano, každé těleso pohybující se podsvětelnou rychlostí se může zastavit např. srážkou s jiným tělesem. Protože ale neutrina interagují velice zanedbatelně jak mezi sebou navzájem, tak s ostatní hmotou, je takováto srážka extrémně málo pravděpodobná. Nic ale nebrání přejít do soustavy pohybující se stejnou rychlostí jako to neutrino, a v této soustavě bude neutrino v klidu. Totéž nelze provést s částicemi pohybujícími se rychlostí světla, protože v principu nelze zkonstruovat žádnou soustavu pohybující se rychlostí světla (dokonce i když ji konstruujeme jako čistě matematický konstrukt, měla by pak spoustu singulárních vlastností, např. energie všech částic s nenulovovou klidovou hmotností by v ní byly nekonečné).
Nejpomalejší neutrina jsou proto podle teorie ta reliktní, která se nezpomalovala srážkami, ale v důsledku rozpínání vesmíru (píšu podle teorie, protože zatím je nikdo nepozoroval). Stejně tak, jako v důsledku rozpínání vesmíru chladnou reliktní fotony, tak stejně tak chladnou reliktní neutrina. Rozdíl je v tom, jak se to chladnutí projevuje. V obou případech se zvětšuje de Broglieova vlnová délka spolu s tím, jak kinetická energie klesá k nule. Částice s nulovou klidovou hmotností si ale stále ponechávají rychlost světla (zmenšování energie se neprojeví jejich zpomalením), zatímco částice s nenulovou klidovou hmotností se čím dál více zpomalují.
Znova ďakujem za odpoveď,
Vladimír Bzdušek,2019-09-18 15:42:15
a teraz už šliapem po pre mňa neznámej pôde: Spomalenie reliktných neutrín je teda úmerné, resp. rovné hodnote Hubble konštanty? A ak fotóny nemôžu spomaliť, ako zmena ich energie súvisí s onou konštantou?
Re: Znova ďakujem za odpoveď,
Pavel Brož,2019-09-18 23:01:50
Jak u neutrin, tak u fotonů, ale i u jakýchkoliv jiných částic, ať už jde o elektrony, protony, neutrony, ba dokonce i u jader, atomů a molekul, můžeme definovat tzv. de Broglieho vlnovou délku - tato veličina je nepřímo úměrná jejich hybnosti. Speciálně u fotonů potom de Broglieho vlnová délka je totéž, jako vlnová délka odpovídající elektromagnetické vlny. de Broglieho vlnová délka určuje interferenční jevy, které lze u příslušných částic pro tu kterou hybnost pozorovat. Tyto interferenční jevy jsou intenzivně využívány v různých oborech, jako je např. neutronová defektoskopie, krystalografie, strukturní analýza, a mnoha jiných.
Tak, jak se vesmír roztahuje, tak se úměrně roztahují i de Broglieho vlnové délky, bez ohledu na to, čeho jsou to de Broglieho vlnové délky, přičemž všechny tyto de Broglieho vlnové délky se rozpínají stejným faktorem, tedy bez ohledu na to, zda patří neutrinům, fotonům či jiným částicím. Ovšem pozor, předpokládáme, že jde o volné částice, protože částice mění své hybnosti, tedy i své de Broglieho vlnové délky, nejen v důsledku rozpínání vesmíru, ale i v důsledku svých srážek. Velikost roztažení de Broglieho vlnových délek je úměrná roztažení prostoru za danou dobu - takže se jedná o kumulativní efekt. Vesmír se ale během své existence nerozpíná stále stejně rychle, rychlost jeho rozpínání se mění - po skončení inflační fáze, kdy se vesmír po kraťoučkou dobu rozpínal exponenciálně rychle, přešel do fáze zpomalovaného rozpínání, která trvala do té doby, dokud měla na rozpínání vesmíru převažující vliv hmota. Zhruba před pěti až sedmi miliardami let ale získala navrch temná energie, jejíž účinek na rozpínání vesmíru je opačný než u hmoty - zatímco hmota rozpínání vesmíru zpomaluje, temná energie ho urychluje. Od té doby se tedy vesmír rozpíná zrychleně.
Kumulativní velikost tohoto rozpínání od nějakého zadaného okamžiku po začátku Velkého třesku až po dnešek je komplikovanou funkcí závislou na parametrech tzv. Standardního kosmologického modelu - tyto parametry se snažíme určovat na základě mnoha různých pozorování, mezi nimiž hrají nejvýznačnější roli tato dvě: měření rudého posuvu vzdálených galaxií a měření anizotropií reliktního (fotonového) záření. Každopádně Hubbleova konstanta neměří kumulativní velikost, nýbrž okamžitou rychlost rozpínání vesmíru - tzn. že Hubbleova "konstanta" se v průběhu rozpínání vesmíru mění (zkrátka řečeno, je to konstanta prostorová, nikoliv časová). Proto není prodloužení de Broglieho vlnových délek částic ani úměrné ani nepřímo úměrné současné hodnotě Hubbleovy konstanty, ale je její velice komplikovanou funkcí.
Fotony sice nemůžou zpomalit, ale jejich energie se snižuje, protože je úměrná jejich hybnosti (a ta je nepřímo úměrná jejich vlnové délce) - tato úměrnost mezi energií a hybností je společnou vlastností platící pro všechny částice s nulovou klidovou hmotností - konstantou úměrnosti je rychlost světla ve vakuu: E=p*c, kde E je energie a p hybnost. Snížení energie se u fotonů projeví snížením frekvence odpovídající světelné vlny, která je opět úměrná energii. Prakticky tento efekt měříme jako kosmologický rudý posuv - čím vzdálenější galaxii pozorujeme, tím jsou jejich spektra posunutá směrem do větších vlnových délek, tedy směrem do menších frekvencí.
U (volných) částic, jader, atd., majících nenulovou klidovou hmotnost, se jejich hybnost sice snižuje naprosto stejným faktorem, jako u těch fotonů, ale energie už se mění jinak - je to dáno tím, že pro tyto částice neplatí jednoduchý vztah E=p*c, ale E=odmocnina(p^2*c^2+m^2*c^4), kde m je klidová hmotnost. V nerelativistické oblasti tento vztah přejde ve známý Newtonovský vztah E=p^2/(2m). Jinými slovy, zatímco pro fotony, ale také i pro ultrarelativistické částice pohybující se rychlostí velice blízkou c, platí, že když se jejich hybnost zmenší tisíckrát, tak se i tisíckrát zmenší jejich energie, tak pro nerelativistické částice platí, že když se jejich hybnost zmenší tisíckrát, tak se jejich energie zmenší miliónkrát.
Pro částice s nenulovou klidovou hmotností také na rozdíl od částic s nulovou platí vztah p = m*v/odmocnina[1-(v/c)^2], kde v je rychlost. Odtud můžeme vyjádřit rychlost jako funkci hybnosti jako v = p*c/odmocnina(p^2+m^2*c^2), který v nerelativistické oblasti přejde ve známý Newtonovský vztah v = p/m. Z tohoto vztahu pak můžeme určit velikost toho zpomalení různých částic v důsledku rozpínání vesmíru. Tak např. pokud za sledované období vezmeme období od vzniku (fotonového) reliktního záření (cca 380 tisíc let po Velkém třesku) po dnešek, tak za tuto dobu se vlnová délka reliktních fotonů zvětšila zhruba tisíckrát. Tzn. že i tisíckrát se za tuto dobu prodloužily de Broglieho vlnové délky všech volných částic - pokud by tedy v té době existovaly např. volné protony nebo elektrony, jejich hybnost by se zmenšila taky tisíckrát, a protože v době vzniku reliktního záření s ním byly v termodynamické rovnováze, tedy měly kinetickou energii odpovídající několika elektronvoltů, což je o mnoho řádů pod jejich klidovou energií, tak se tyto částice už tehdy pohybovaly nerelativistickými rychlostmi - proto pro ně už tehdy šel s dostatečnou přesností použít nerelativistický vztah v=p/m. Protože od té doby se jejich hybnost zmenšila tisíckrát, tak i jejich rychlost se zmenšila tisíckrát. Bohužel právě provedená úvaha má pouze pedagogický význam, ve skutečnosti pro ni nemáme splněné předpoklady - v době vzniku reliktního záření byla průměrná hustota částic ve vesmíru 1000^3=miliardkrát větší než dnes - zatímco v dnešním vesmíru připadá řádově jeden proton a jeden elektron na kubický metr, v té době to bylo na jeden kubický milimetr. Takže za tu doby nějaké ty srážky u elektronů a protonů zcela určitě proběhly - na rozdíl od osvobozených reliktních fotonů, pro něž náhle celý vesmír zprůhledněl a které se od té doby volně pohybují, tedy elektrony a protony, a ani jádra deuteria a další lehká jádra, nebylo možno považovat za volné.
Podíváme-li se podobným způsobem na reliktní neutrina, jejich dnešní předpokládaná teplota vychází cca 1,95 K (viz např. https://cs.wikipedia.org/wiki/Reliktn%C3%AD_neutrina), což odpovídá dle Boltzmanova vztahu E=(3/2)k*T, kde k je Boltzmanova konstanta, kinetické energii 2,5*10^-4 eV. Nyní hodně záleží na tom, jak velká je jejich klidová hmotnost. Pokud bude řádově v desetinách eV, tak by to znamenalo, že dnes se pohybují rychlostmi řádově stokrát menšími, než je rychlost světla - konkrétně např. pokud by jejich klidová hmotnost byla 0,67 eV, pohybovala by se dnes rychlostí 0,027 c, tedy cca 8100 km/s, čili cca dvěstěkrát rychleji, než je rychlost přilétajících komet a meteoritů. Tato rychlost se zdá být velká, ve skutečnosti ale i obyčejné elektrony ve starých katodových (tj. těch „hlubokých“) monitorech docilovaly rychlosti až 35 procent rychlosti světla, tedy cca třináctkrát větší. Pokud by ale neutrina měla výrazně menší klidovou hmotnost, řekněme 0,001 eV, potom by se pohybovala rychlostí 0,71 c, tedy stále relativistickými rychlostmi.
Vďaka, prežul som to
Vladimír Bzdušek,2019-09-19 22:44:03
a napodiv, celkom som to pochopil! Máte talent na vysvetlenie zložitého.
Re: Re: Ďakujem za odpoveď,
Lada 1,2019-09-19 14:35:53
"...např. energie všech částic s nenulovovou klidovou hmotností by v ní byly nekonečné" Je to myšleno takto? "...např. energie každé z částic s nenulovovou klidovou hmotností by v ní byla nekonečná" , nebo je to myšleno skutečně jako suma energií všech daných částic?
Re: Re: Re: Ďakujem za odpoveď,
Pavel Brož,2019-09-19 15:06:25
Je to myšleno tak, že energie každé z částic, která má nenulovou klidovou hmotnost, by v takové soustavě byla nekonečná. Kromě této singulární vlastnosti má ale soustava pohybující se rychlostí světla spoustu dalších singularit, tak např. veškerý okolní prostor by v ní byl o jednu dimenzi chudší, protože dimenze ve směru pohybu soustavy by se Lorentzovskou kontrakcí zkrátila na nulu, a dále všechny procesy v okolním vesmíru by "zamrzly v čase", opět v důsledku Lorentzovské dilatace, tentokrát času. Popis v takové soustavě prostě vede k mnoha matematickým a logickým sporům, podobně, jako když bychom v rovnicích krátili nulu (např. rovnice 0x1=0x2 platí, ale po vykrácení nulou bychom získali nesmyslný výsledek 1=2). To, že je soustava pohybující se rychlostí světla nepřípustná, tedy není jen nějaké technické omezení ani důsledek konzervativnosti fyziků, má to své vlastní mnohem hlubší důvody.
Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Nedbal,2019-09-19 19:48:57
Vážený pane Broži,
mě ty oscilace neutrin nějak nejdou do hlavy. Jak se může tauonové neutrino zbavit hmotnosti, aby se chovalo jako elektronové, a obráceně, jak může elektronové neutrino být někdy tauonovým, které je cca 3000x těžší, nebo mionovým cca 200x těžším? Přece jediná možnost je výměna rychlosti za hmotnost, ale podmínkou je nějaká další interakce, která to umožní. I kdybych přijal vysvětlení, že neutrino je namícháno z 1/3 tauonové, z 1/3 mionové a 1/3 elektronové, tak vlastně by šlo říci, že je jen jediný typ neutrina, mix. Kdyby reakcí p+p=D vznikala jak elektronová, mionová a tauonová, pak by ta reakce musela mít jiný energetický obsah, než udávaný. Totéž při beta +/- rozpadech jader, koneckonců i z toho T. Tak jak to tedy je, nemáme v tom nějakou chybu?
Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Brož,2019-09-19 23:40:49
Dobrý den, nikoliv, jedna dílčí chyba je už ve Vašem předpokladu, že tauonové neutrino 3000x těžší než elektronové, a mionové že je 200x těžší než elektronové. Tyto hmotnostní poměry totiž platí pro nabité leptony tau, mí a elektron, nikoliv pro jejich neutrina. Hmotnostní poměry neutrin dodnes neznáme, naopak pokud bychom předpokládali platnost odhadů získaných jak z pozemských neutrinových experimentů, tak nepřímo plynoucích z kosmologických pozorování, tak to vypadá, že hmotnosti všech tří neutrin budou velice blízké.
Nicméně tato chyba není nijak zásadní, i kdyby totiž opravdu mezi jejich hmotnostmi byly až tak velké rozdíly, jaké uvádíte, tak by to stejně na možnosti je experimentálně odlišit na základě jejich rychlosti nic nezměnilo. Všechna tři neutrina totiž mají v reakcích, ve kterých je detekujeme, aspoň o šest řádů větší energii, než je jejich klidová energie, z čehož plyne, že se pohybují rychlostmi odlišnými od světelné pouze o méně než 10^-12 c. Např. elektronové neutrino vzniklé v jádru Slunce dorazí k Zemi za cca 500 sekund, tj. 8 minut a 20 sekund. Z kosmologie víme, že součet hmotností všech tří neutrin by měl být menší než 2 eV, předpokládejme, že nejhmotnější z nich má klidovou hmotnost zrovna ty 2 eV, a další dvě jsou 200x a 3000x lehčí. Nechť má toto nejtěžší neutrino energii 2 MeV, potom se pohybuje rychlostí pouze o 0,5*10^-12 c menší než je rychlost světla c. Takže toto neutrino bude na Zemi o 500*0,5*10^-12 = 2,5*10^-10 sekund (tedy o čtvrtinu nanosekundy) později, než by tu bylo světlo, pokud by mu v cestě z nitra Slunce nic nepřekáželo (ve skutečnosti to světlu trvá řádově tisíc let, než se v procesech opakované absorpce a emise prokouše z jádra k povrchu, ale o to teď nejde). Zdůrazňuji, že to zpoždění čtvrt nanosekundy platí pro to nejtěžší neutrino, ta lehčí neutrina budou mít zpoždění menší, protože se budou pohybovat větší rychlostí, než to nejtěžší (samozřejmě ale stále rychlostí podsvětelnou). I kdyby mělo nejlehčí neutrino nulovou klidovou hmotnost (pro oscilace neutrin postačí, aby dvě neutrina měla nenulové klidové hmoty, nemusí je mít nenulové všechna tři), tak se oproti němu to nejtěžší proto zpozdí pouze o čtvrt nanosekundy, čemuž odpovídá „délkové“ zpoždění pouze o 7,5 cm (protože za jednu nanosekundu urazí světlo pouhých 30 cm – teď zcela odbočím, ale skutečnost, že za jednu nanosekundu urazí světlo pouhých 30 cm se mimochodem promítá i do konstrukce těch nejvýkonnějších superpočítačů, které prostě musí počítat s tím, že přenést data mezi procesory ve dvou sousedících počítačových skříních nejde tak rychle, jak rychle umíme taktovat procesory).
To zpoždění čtvrt nanosekundy anebo ekvivalentně 7,5 cm je mnoho řádů pod našimi současnými detekčními schopnostmi v experimentech týkajících se slunečních neutrin, už jenom z toho důvodu, že nemáme jak kontrolovat, kde ve Slunečním jádře a přesně kdy se to které neutrino zrodilo. Umíme to sice s mnohem větší přesností kontrolovat v experimentech v urychlovačích, kdy vygenerujeme svazek např. mionů, ten pak odchýlíme na nějaký vzorek, kde se z jejich srážek vyprodukují příslušná neutrina, a ta potom detekujeme – možná si vzpomínáte na kauzu s údajně nadsvětelnou rychlostí neutrin v experimentu v Gran Sasso, Vladimír Wagner o ní psal i zde na oslu v těchto článcích:
http://www.osel.cz/5896-prekracuji-neutrina-mezni-rychlost-svetla.html
http://www.osel.cz/5993-nadsvetelne-rychlosti-neutrin-prezily-prvni-zkousku.html
http://www.osel.cz/6216-opet-neutrina-jedno-potvrzeni-a-jedno-popreni.html
a redakce potom zde:
http://www.osel.cz/6143-nadsvetelnou-rychlost-neutrin-ma-na-svedomi-spatne-zapojeny-kabel.html
(blíže viz https://en.wikipedia.org/wiki/Faster-than-light_neutrino_anomaly, na vině byl nakonec špatně zapojený kabel, který způsobil problémy v časové synchronizaci měření)
V případě těchto experimentů sice umíme mnohem přesněji určit dobu vzniku neutrin, nicméně vzdálenost, na které je detekujeme, je příliš malá (i když na pozemské experimenty stále úctyhodných 731 km), takže opět neumíme spolehlivě rozlišit doby letu rozdílných druhů neutrin.
Co se týče toho, v jakých stavech se neutrina rodí a zanikají, tak tyto stavy jsou přesně elektronové, mionové nebo tauonové neutrino podle příslušné reakce. Např. rozpadem mionu vznikne vždy pouze čisté mionové neutrino, žádný mix elektronového, mionového a tauonového. Podobně rozpadem tauonu vznikne pouze čisté tauonové neutrino, a v jaderných reakcích typu beta plus rozpad a jaderná fúze vzniká čisté elektronové neutrino (v normálním beta minus rozpadu a v jaderném štěpení probíhajícím v jaderných reaktorech zase vzniká čisté elektronové antineutrino). Tyto stavy jsou „čisté“ z hlediska „vůně“ (flavor), což je charakteristika jednotlivých částicových generací, nicméně nejsou to čisté stavy z hlediska energie, tedy stavu mající ostrou hodnotu energie. Bylo to docela překvapení, když se zjistilo (poprvé nikoliv u neutrin, ale u kvarků), že příroda může vytvářet částice ve stavech s „rozmazanou“ hodnotou energie. To, že existují kvantově mechanické stavy, které nemají ostrou hodnotu energie, bylo známo už dlouho, ale nepředpokládalo se to u kreace ani anihilace částic. Nicméně protože se tato hypotéza osvědčila u kvarků, kde uměla velice dobře vysvětlit např. rozpady baryonů a mezonů, tak pro použití neutrin už nebyla pro fyziky tak exotická – jedinou podmínkou pro ni byla nenulovost klidových hmot aspoň dvou neutrin. Plus navíc z této hypotézy automaticky plyne oscilace těch neutrin. Mimochodem, podobnou oscilaci umíme měřit i u neutrálních Kaonů (dříve nazývaných K-mezony), i když zde je způsobena něčím jiným, konkrétně drobným narušením CP symetrie, které se projevuje malilinkým hmotnostním rozdílem v hmotnosti vlastních energetických stavů těchto Kaonů (tak jako jsou elektronové, mionové i taunové neutrino mixem ostrých energetických stavů neutrino_1, neutrino_2, neutrino_3, jsou i neutrální Kaon a jeho antičástice mixem dvou odpovídajících ostrých energetických stavů označených K01 a K02, a tyto stavy mají malilinko odlišné klidové hmotnosti).
Vrátím-li se k neutrinům, tak konkrétně třeba elektronové neutrino je mixem ostrých energetických stavů neutrino_1, neutrino_2, neutrino_3. Protože tyto stavy mají rozdílnou klidovou hmotnost, po čase se od sebe prostorově separují. Než se ale rozseparují, můžeme na různost jejich klidových hmotností usuzovat z těch oscilací, které jsou citlivé na rozdíl klidových hmotností. Jedná se totiž o to, že fáze každého z energeticky ostrých neutrinových stavů neutrino_1, neutrino_2, neutrino_3 se mění rychlostí úměrnou jeho klidové hmotnosti, a čistě algebraicky se pak dá ukázat, že kvadrát vlnové funkce je pak modulován faktorem cos (delta_m*t), kde delta_m je rozdíl těch hmotností a t je čas.
A jak je to tedy s tou finální separací těch neutrin? Předpokládejme, že uděláme obdobu experimentu v Gran Sasso, akorát že neutrina sice budeme nadále generovat v CERNu, ale místo jejich detekce, tedy laboratoř v Gran Sasso, přemístíme na Pluto zrovna, když bude v aféliu (necelých 50 astronomických jednotek, tedy padesátkrát dále, než je vzdálenost Země-Slunce). Předpokládejme, že budeme umět určit dobu zrodu neutrin s přesností na jednu nanosekundu, tzn. podélná nepřesnost v určení polohy neutrin bude cca 30 cm. Dejme tomu, že nejtěžší bude neutrino_3 a že bude mít už zmíněnou klidovou hmotnost 2 eV, další dvě nechť budou o několik řádů lehčí. Potom to neutrino_3 dorazí na Pluto se zpožděním 7,5 cm x 50 = 375 cm za těmi dvěma lehčími. Protože podle našeho předpokladu je podélná neurčitost polohy pouze 30 cm, tak na Plutu už by bylo to nejtěžší neutrino odseparováno od těch zbývajících o cca 375-30=345 cm – už by nám tedy neoscilovala všechna tři neutrina, ale jenom ty první dvě lehčí, pokud by se jejich vlnové funkce stále ještě překrývaly, zatímco to nejtěžší už by k jejich oscilacím nepřispívalo, protože ta první dvě by ho nechala cca tři a půl metru za sebou.
Z právě uvedeného příkladu vyplývá, proč dnes neumíme rozseparovat elektronové neutrino na jeho vlastní energetické stavy neutrino_1, neutrino_2 a neutrino_3 (stejně tak samozřejmě neumíme rozseparovat ani mionové a ani tauonové neutrino). Teoreticky bychom tuto separaci mohli udělat u kosmických neutrin, která k nám přilétají z obrovských mezihvězdných vzdáleností – zde je pro změnu problém v intenzitě svazku, zatím se nám taková neutrina podařilo identifikovat s konkrétním astronomickým zdrojem jenom jednou, a to při sledování exploze supernovy SN1987A, a i tehdy se podařilo zachytit pouze 25 antineutrin, což je na jakékoliv oscilační měření žalostně málo (blíže viz https://en.wikipedia.org/wiki/SN_1987A#Neutrino_emissions). Takže do té doby, než postavíme laboratoř na tom Plutu, tak jsme odkázáni jenom na oscilační experimenty, ve kterých nejsou jednotlivé ostré energetické stavy rozseparovány.
Na závěr bych ještě velice rád udělal jednu podstatnou zmínku – dobrou třetinu svých vědomostí o neutrinech, možná i více, jsem získal už před mnoha lety z popularizačních článků Vladimíra Wagnera, viz zde: https://ojs.ujf.cas.cz/~wagner/popclan, Vladimírovi tímto velice děkuji. Vystudoval jsem teoretickou fyziku, a během mého studia byla terčem mého zájmu tehdy populární teorie superstrun, ze které jsem obhájil i diplomku. Studium reálných částicových interakcí mě tehdy nepřišlo důležité, protože jsem měl jako mnoho tehdejších mladých studentů naivní představu, že až bude někdy teorie superstrun dokončena, tak že hravě vysvětlí všechny pozorované částicové děje, a event. i ty kosmologické. Jak bláhový jsem byl. Teprve až několik let po absolutoriu jsem začal objevovat velice krásnou a ze strany strunových fyziků neprávem opomíjenou fyziku, která se zakládá na reálných částicových pozorováních, nikoliv pouze na spekulacích o takovém či onakém počtu nadbytečných dimenzí našeho prostoročasu, spolu se spekulováním, jak to udělat, aby ty nadbytečné dimenze nezbytné pro logickou integritu strunových teorií nebyly reálně pozorovatelné. A byly to právě popularizační články Vladimíra, které mě tuto oblast otevřely. Je mi velikou ctí, že tento úžasný zdroj mnoha podrobných informací o světě částic mohu doporučit i všem dalších zájemcům o tuto oblast.
Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Nedbal,2019-09-20 20:53:25
Vážený pane Broži,
děkuji za obšírný výklad a uvedení mého omylu, kdy jsem zaměnil hmotnosti neutrin za hmotnosti mateřských leptonů, na správnou míru. Pokud bych ještě měl dotaz na upřesnění - když se rozpadají ty dva těžší leptony, vzniká v konečné fázi elektron a příslšná neutrina - předpokládám, že se o tu hmotu/energii nějak podělí, to by bylo asi jasné.
Ale, když se podíváme na standardní model, jsou tam tři rodiny částic, a z toho je jen jedna rodina stabilní - nejsou ty vyšší rodiny vlastně jen nějak "virtuální", mám na mysli, zda to vlastně nejsou částice té stabilní rodiny energeticky "podšprajcované" do nějakého metastabilního stavu, ve kterém se udrží jen chviličku, ve které je občas registrujeme, a pak se energie zbavují a konečná fáze jsou ty základní, stabilní "rodina"? Můžeme připustit, kdybychom měli dostatečnou energii, že by se mohly vytvořit ještě další, ještě vyšší energií nabité částice ekvivalentní těm stabilním? Hledám v tom důvod, proč takové nestabilní částice (jako třeba i zmíněný mion a tauon) mají vůbec nějakou funkci, když ve Vesmíru, pomineme -li zase extrémy, vůbec nejsou obsaženy?
Děkuji a přeji příjemný víkend.
Pavel Nedbal
Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Vladimír Wagner,2019-09-21 14:33:25
Pokusím se odpovědět místo Pavla Brože. Jak jste uváděl, poměry mezi hmotnostmi tauonu, mionu a elektronu jsou hodně velké, dominantně se rozpadají právě na na leptony z nižší hmotností a neutrina. To znamená, že dominantní část klidové energie těžšího nabitého leptonu se přemění na kinetickou energii produktů. To rozdělení energií mezi produkty je dáno kinematikou.
Pokud jde o počet nabitých leptonů (tedy otázka, jestli existuje kromě tří známých, tedy elektronu, mionu a tauonu ještě nějaký těžší), tak tam je asi docela jasno. Standardní model známé částice grupuje do tří rodin. V každé jsou dva kvarky a jeden nabitý a jeden neutrální lepton (neutrino). Pokud by existovala další generace, musela by zase obsahovat dva kvarky, nabitý lepton a neutrino. Pokud bychom předpokládali, že budou mít i další neutrina stejné vlastnosti, jako první tři, tedy hrozně malou hmotnost, tak další existovat nemohou. Boson Z0 se totiž rozpadá i kanálem neutrino a odpovídající antineutrino. A jeho doba života (která je dána i počtem možných rozpadů na neutrino a antineutrino) ukazuje, že existují jen tři neutrina s odpovídající malou hmotností.
Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Brož,2019-09-21 22:03:34
Dobrý den, na otázku proč experiment podporuje existenci pouze tří rodin standardního modelu, odpověděl už Vladimír Wagner, já se nyní zaměřím na Vaši otázku, jestli ta druhá a třetí rodina nejsou jenom nějak energeticky podšprajcované neboli excitované stavy té první rodiny. Taková představa je v rozporu jak se stávající teorií, tak s experimentálními daty. S teorií, tj. standardním modelem, je v rozporu proto, že podle něj jsou částice mion, tauon a kvarky s, c, b a t částicemi sice nestabilními, ale přesto elementárními, tedy bezstrukturními – standardní model neumožňuje vysvětlit větší klidové hmotnosti částic druhé a třetí rodiny coby excitované stavy částic rodiny první (tedy elektronu a jeho neutrina a kvarků u a d), právě protože podle něj tyto částice nemají žádnou vnitřní strukturu, není tedy co a jak excitovat. Nicméně standardní model je jenom teorie, lze si představit, že by byl nahrazen teorií jinou, podle níž by leptony i kvarky byly částicemi nikoliv elementárními, ale složenými – taková teorie dokonce byla už v roce 1974 navržena a později známá pod názvem preonová teorie (viz https://en.wikipedia.org/wiki/Preon), a jedním z jejích dvou spoluautorů nebyl nikdo menší, než pozdější nositel Nobelovy ceny Abdus Salam (kteroužto cenu ale nedostal za preonovou teorii, nýbrž za své význačné příspěvky k standardnímu částicovému modelu).
Preonová teorie ale záhy po svém zrodu nepřežila střet s experimentem, který potvrdil bodovost leptonů a kvarků s přesností pod 10^-18m. Pokud by kvarky a leptony nebyly elementární, ale šlo by o vázané stavy preonů, a přitom by tyto vázané stavy měly být menší, než těch 10^-18 m, pak by podle Heisenbergova principu neurčitosti musely mít tyto stavy klidovou hmotnost aspoň 400 tisíckrát větší, než je klidová hmotnost elektronu (a tedy cca dvěstěkrát větší, než je klidová hmotnost protonu), což je spor. Úvaha, ze které to plyne, je podobná té, ze které plyne odhad velikosti atomu – velikost elektronového obalu např. základního stavu atomu vodíku koresponduje s neurčitostí hybnosti elektronu v tomto obalu, přičemž obě tyto neutrčitosti se dají spočíst z řešení Schrodingerovy rovnice popisující vázaný stav elektronu v atomu, a obě vyhovují – tak jak to kvantová teorie nekompromisně vyžaduje – Heisenbergovu principu neurčitosti. Pokud bychom totéž provedli pro hypotetický vázaný stav preonů v dejme tomu elektronu, dostali bychom výše zmíněný spor – buď by tento vázaný stav musel mít hmotnost rovnou hmotnosti elektronu, ale cca 400 tisíckrát větší velikost než experimentálně ověřených 10^-18 m, anebo by by měl tu velikost cca 10^-18 m, ale pak by zase musel mít 400 tisíckrát větší hmotnost, než je hmotnost elektronu.
Dalším argumentem proti představě, že částice vyšších rodin jsou excitovanými stavy částic rodiny první, je to, že takovéto excitované stavy by se v principu mohly deexcitovat vyzářením gama fotonu – nic by tomu nebránilo, protože až na neutrina jsou všechny leptony nabitými částicemi, tzn. že interagují i prostřednictvím ať už virtuálních, nebo i reálných fotonů. Neexistoval by žádný způsob, který by zabránil deexcitaci dejme tomu mionu na elektron prostřednictvím vyzáření gama fotonu, a ze známé hmotnosti mionu a elektronu by se dal udělat i odhad četnosti takové deexcitace, která by byla řádově ne moc vzdálená četnosti standardního rozpadu mionu na elektron za současného vzniku mionového neutrina a elektronového antineutrina. Problém je v tom, že zatímco ten druhý zmíněný rozpad se pozoruje naprosto běžně, tak rozpad mionu za vzniku odpovídajícího gama fotonu se nepozoroval nikdy.
Ještě se vrátím k otázce stabilnosti první rodiny kontra nestabilnosti druhé a třetí rodiny. Není to úplně pravda, že by částice první rodiny byly stabilní, zatímco částice druhé a třetí nestabilní. V první rodině máme elektronové neutrino, elektron, kvark u a kvark d. A kvark d je nestabilní, rozpadá se na kvark u, elektron a elektronové antineutrino – důsledkem tohoto rozpadu je známý beta (minus) rozpad, kdy se neutron složený z kvarků udd, rozpadá na proton složený z kvarků uud, elektron a elektronové antineutrino. Naopak ve druhé a třetí rodině máme stabilní mionové neutrino a stabilní tauonové neutrino, ty se na nic nerozpadají. Mohlo by se zdát, že tato dvě neutrina stabilní nejsou, protože jak víme, neutrina oscilují. Jenže tato oscilace je způsobena pouze jako důsledek toho, že se u jednotlivých složek neutrin, tj. stavů s ostrou hodnotou energie neutrino_1, neutrino_2 a neutrino_3, různou rychlostí mění fáze vlnové funkce. Tato oscilace je periodická, tzn. že např. mionové neutrino se po konečném čase opět zregeneruje jako mionové, elektronové pak znovu jako elektronové, tauonové jako taunové – blíže viz grafy zde https://en.wikipedia.org/wiki/Neutrino_oscillation#Three_neutrino_probabilities .
Ve skutečnosti je stabilita či nestabilita částic podmíněna jednak povolenými typy Feynmanových diagramů v té které teorii, a jednak relativními hmotnostmi částic. Nejlépe se to dá uvést na příkladu. Standardní model např. obsahuje interakční vrchol (což je nejjednodušší typ Feynmanova diagramu), který sestává z linie elektronu, elektronového neutrina a intermediálního bozonu W-, které jsou jedním svým koncem spojené v jednom bodě. Na tomto obrázku https://en.wikipedia.org/wiki/File:Standard_Model_Feynman_Diagram_Vertices.png je to prostřední typ vrcholů, kde W je v našem příkladu bozon W-, L je elektron a ný je elektronové neutrino. Předpokládejme pro jednoduchost, že elektronové neutrino má klidovou hmotnost 1 eV, dále víme, že elektron má klidovou hmotnost cca 511 keV, a intermediální bozon W- má klidovou hmotnost 80 GeV. Proto se ve standardním modelu rozpadá bozon W- na elektron a jeho antineutrino, zatímco další dva typy rozpadů popisované stejným diagramem – rozpad antineutrina na W- a pozitron (event. neutrina na W+ a elektron) a rozpad elektronu na W- a elektronové neutrino - jsou energeticky nepřípustné a proto neprobíhají. Pokud by ale intermediální bozon W- měl klidovou hmotnost, která by se od hmotnosti elektronu lišila o méně než hmotnost elektronového neutrina, pak by tento bozon byl další stabilní částicí standardního modelu, protože by neexistoval způsob, jak by se mohl rozpadnout, aby byl přitom splněn zákon zachování energie. To ale není všechno – pokud by klidová hmotnost bozonu W- byla menší než hmotnost elektronu, a to o více, než je hmotnost jeho neutrina, tak by se navíc elektron stal nestabilní částicí. Rozpad elektronu na bozon W- a elektronové neutrino by totiž jednak byl umožněn existencí příslušného Feynmanova diagramu (který jak již víme ve standardním modelu existuje), a navíc by byl energeticky přípustný, tudíž by podle teorie musel nevyhnutelně probíhat.
Změna hmotnosti bozonu W- (a bozonu W+, který musí mít klidovou hmotnost stejnou, jako W-) by si samozřejmě vyžádala změnu i jiných parametrů – je tomu tak proto, že zatímco hmotnosti všech fermionů jsou ve standardním modelu volnými parametry, které se musí nafitovat měřením, tak pro hmotnosti bozonů a pro velikosti různých dalších konstant to už obecně neplatí, protože existuje množství algebraických vztahů, jejichž platnost plyne z požadavku konzistence tohoto modelu. Nicméně po takové změně bychom stále měly formálně týž standardní model, se stejnou logickou konzistencí, se stejnými formulemi předpovídajícími výsledky všech experimentů, a jediné, co bychom v těchto formulích museli změnit, by byla hmotnost bozonu W-, dále volitelně hmotnost bozonu Z a Higgsova bozonu, povinně ale hodnoty některých dalších konstant.
My samozřejmě z experimentů víme, že bozon W- není lehčí než elektron, ale že je cca 156 tisíckrát těžší. Nicméně odpověď na otázku, proč tomu tak je, standardní model nenabízí. Lze se sice setkat s různými pseudoodpověďmi, jako že hmotnost intermediálních bozonů je určena velikostí narušení elektroslabé symetrie, ale to není skutečná odpověď, protože tato teorie nepředpovídá velikost narušení té symetrie – pokud by byla narušená výrazně menší měrou, bozon W- by mohl být klidně lehčí než elektron. Existuje i jiná pseudoodpověď, a to, že velikost hmotnosti bozonu W- je spoluurčena velikostí hmotnosti Higgsova bozonu (viz první vztah v tomto odstavci https://en.wikipedia.org/wiki/W_and_Z_bosons#Predicting_the_W_and_Z ). I toto je ale jenom kopnutí míče do autu, protože standardní model nepředpovídá velikost hmotnosti Higgse (jiná otázka je, že z konkrétních experimentů a z konkrétních hodnot ostatních parametrů následně nějaká hodnota pro hmotnost Higgse vychází, nicméně stále platí, že hmotnost Higgse je v principu volným parametrem standardního modelu, který sice spoluurčuje hodnoty jiných parametrů, ale sám musí být nafitován měřením).
Vidíme tedy, že stabilita těch kterých částic ve standardním modelu vůbec nesouvisí s jejich umístěním v té které rodině, tedy s jejich pozicí v oné pomyslné „periodické tabulce částic“, ale že je především ovlivněna relativními velikostmi hmotností částic, z nichž většinu standardní model nepředpovídá (hmotnosti všech fermionů jsou volné úplně, a hmotnosti bozonů se dají změnit za současné změny jiných parametrů teorie).
Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Nedbal,2019-09-21 23:40:59
Vážení pánové Broži a Wagnere,
děkuji za vyčerpávající vysvětlení interakcí ve standardním modelu. Ve své neznalosti jsem si mnohé představoval chybně (zejména představa o vyšších rodinách v SM). Takže, jen ve stručnosti, snad jsem pochopil, co je podstatné, kvarky jsou nedělitelné, bodové částice, preony neexistují. Druhá a třetí rodina kvarků, miony a tauony jsou nestabilní, z leptonů vyšších rodin jsou stabilní jen neutrina. Stabilita první rodiny platí mimo leptonů pro d-kvarky v protonu, d kvark je v neutronu nestabilní (ale zase se přece může změnit za jistých podmínek na d-kvark při přeměně protonu na neutron, ale v p-p=D reakci musí tam přiletět neutrino, nebo stačí energie srážky?). Mám takový nepříjemný pocit, že se nám v rámci standardního modelu nepodaří vytvořit nějaké exotické stabilní částice, které by se nám mohly hodit, budí to dojem konečné stanice. Nicméně, i tak je SM úžasné dílo.
Děkuji.
Pavel Nedbal
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Brož,2019-09-22 00:48:48
Dobrý den, ohledně otázky u té p-p reakce, tak tam probíhá beta plus rozpad, kdy se naopak lehčí kvark u rozpadá na těžší kvark d, pozitron a elektronové neutrino (zatímco v beta minus rozpadu se těžší kvark d rozpadá na lehčí kvark u, elektron a elektronové antineutrino). Jak je vůbec možné, že se může lehčí kvark rozpadnout na těžší kvark, a ještě zbude dost energie na vyprodukování pozitronu a neutrina?
Řešením této záhady je v případě reakce p + p = D + (e+) + ny (kde p je proton, D deuterium, e+ pozitron a ny elektronové neutrino) hmotnostní defekt deuteria, který je způsobený zápornou vazebnou energií přitažlivé silné interakce působící mezi protonem a neutronem. Díky tomuto efektu je tato reakce exotermní, tzn. že v celkové bilanci produkuje více energie, než spotřebovává, což můžeme snadno ověřit – na levé straně máme klidovou hmotu dvou protonů, tedy 2x938,272=1876,544 MeV, zatímco na pravé straně máme deuterium s hmotností 1875,612 MeV (je o 2,225 MeV lehčí než součet hmotností protonu a neutronu, a to právě kvůli zmíněnému hmotnostnímu defektu), dále tam máme pozitron s klidovou hmotností 0,511 MeV a neutrino s klidovou hmotností 1 eV. Na pravé straně máme tedy 1876,123001 MeV čistě jen v klidových energiích, což je o 0,421 MeV méně, než na levé straně. Proto je tato reakce energeticky možná.
Samozřejmě ačkoliv je tato reakce exotermní, musíme těm dvěma vstupujícím protonům dodat obrovskou energii, abychom překonali jejich odpudivou Coulombickou bariéru a přiblížili je na vzdálenost, kde nad elektromagnetickým odpuzováním začne vítězit přitahování silné interakce. Díky nutnosti vystoupat na ten vysoký energetický vrchol, než se můžeme spustit dolů na jeho druhé straně a realizovat výsledný energetický zisk, je tato reakce velmi špatně realizovatelná. Každopádně ale tato reakce není podmíněna vstupem neutrina, stačí k ní jenom energie srážky dostačující na to zdolání toho energetického vrcholu.
Beta plus rozpad probíhá spontánně i u mnoha nestabilních izotopů. Opět si můžeme položit otázku, jak je možné, že lehčí proton se rozpadne na těžší neutron, a ještě zbude energie na produkci pozitronu a neutrina. I zde je odpověď stejná – může za to hmotnostní deficit, přesněji řečeno v tomto případě rozdíl hmotnostních deficitů původního a výsledného jádra. Z původního nestabilního jádra s malým hmotnostním deficitem vznikne jádro s větším hmotnostním deficitem, přičemž ten rozdíl pokryje klidovou energii pozitronu a neutrina, a ještě zbude na jejich kinetické energie. Můžeme si to představit velice zhruba tak, že protony i neutrony v jádře zaplňují energetické slupky podobně, jako to dělají elektrony v elektronovém obalu. Zásadním rozdílem mezi elektronovými slupkami a těmi slupkami v jádře je ten, že v jádře máme jakoby dva paralelní řebříčky slupek, jeden pro protony a druhý pro neutrony. Představme si jádro, které má proton na nějaké energeticky vysoké protonové slupce, který ale nemůže skočit na nižší protonovou slupku, protože ty jsou už zaplněné jinými protony. Dejme tomu, že má ale pod sebou volnou neutronovou slupku, s dostatečně velkým energetickým odstupem, který by umožnil jednak jeho transmutaci na těžší neutron, plus aby to bylo možné, musí taky zbýt na vyprodukování pozitronu a neutrina. Pokud tam taková hladina je, původní jádro se tímto způsobem rozpadne, tzn. že jeden z původních protonů se změní sice na těžší neutron, ale na o tolik nižší energetické hladině, že ještě zbude na vyprodukování pozitronu a neutrina, bez něhož by reakce nemohla proběhnout.
Přesně tohle je důvod, proč ačkoliv se volný proton nemůže rozpadnout na neutron, pozitron a neutrino, tak v mnoha izotopech to možné je. Na rozdíl od volných částic totiž ve vázaných systémech musíme vzít v potaz i změny ve vazebné energii, nevystačíme si pouze s bilancí klidových hmotností komponent těch vázaných systémů.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Vladimír Wagner,2019-09-22 08:10:02
Možná bych doplnil Pavla. V daném případě využívání termínu rozpad je historický artefakt. Lépe by bylo využívat pojem přeměna. Rozpad navozuje představu, že se rozdělil komplexní systém na části, které v něm existovaly. To však v případě "rozpadu" beta nebo "rozpadu" kvarku" není pravda. elektron či neutrino v jádře nejsou.
Pak je třeba zdůraznit, že v přírodě je možná každá přeměna, která je dovolena zákony zachování. Tedy spojení dvou protonů do deuteronu za přeměny jednoho z nich v neutron při vzniku pozitronu a neutrina je z energetického hlediska možné (jak popisuje Pavel Brož) a není zakázáno zákony zachování. Jen je třeba připomenout, že při této přeměně se přeměňuje jeden kvark na jiný. Při tom se porušuje zákon zachování vůně kvarku, který však může porušovat slabá interakce. Proto tato reakce i beta rozpad mohou probíhat jen slabou interakcí. Ta je však velmi slabá a proto mají tyto procesy velmi málo pravděpodobné.
Pavel Brož mluvil o nutnosti mít dostatek energie pro překonání elektrostatického odpuzování (coulombovské bariery). Je třeba zdůraznit, že v daném případě nemusí mít proton energii nutnou pro úplné překonání coulombovské bariery. Stačí mu (a většinou třeba ve Slunci, kde tyto reakce probíhají) menší energie, protože barieru překonává kvantovým tunelováním. To je další důvod, proč má tato reakce třeba ve Slunci tak malou pravděpodobnost a jen díky jeho velkému objemu tam probíhá ve velkém množství.
A teď zpět k zákonům zachování. To, že mimo jádro skončí baryony (částice podobné neutronu a protonu) u protonu, je dáno tím, že proton je nejlehčí z baryonů. I když existují lehčí částice (elektron a neutrina), jsou to leptony a rozpadem na ně by proton narušil zákon zachování baryonového čísla, který nemůže narušit žádná z interakcí. Jen pro úplnost bych napsal, že se předpokládá velmi slabé narušení i tohoto zákona zachování a rozpad protonu s extrémně dlouhým poločasem rozpadu. Zatím však tento rozpad pozorován nebyl.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Nedbal,2019-09-22 13:18:44
Vážení pánové Broži a Wagnere,
děkuji, toto všechno je jasné. Rozhodující je energetické zabarvení, směr je k větší stabilitě. Rovněž chápu, že při přeměně p na n v jádru pozitron nevyskočí z protonu, nýbrž se utvoří z nábojové rovnováhy a hmotnostního deficitu. Jen jsem ještě někde četl, že se neutron může vytvořit srážkou protonu s neutrinem - toto je ale asi málo pravděpodobné ne?
Jen jedna malá sci-fi myšlenka - dovedli byste připustit, jestli by se mohla vytvořit nějaká dostatečně stabilní "nová hmota" tvořená něčím jiným než u a d?
Zdravím Vás a děkuji.
Pavel Nedbal
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Brož,2019-09-22 14:25:29
Ano, neutron se může vytvořit srážkou protonu s antineutrinem (nikoliv neutrinem), a ačkoliv je tato reakce velmi málo pravděpodobná, je to ve skutečnosti způsob, jak antineutrina detekujeme, viz např. zde https://en.wikipedia.org/wiki/Kamioka_Liquid_Scintillator_Antineutrino_Detector . Možná ale máte na mysli srážku volných protonů pohybujících se v mezihvězdném prostoru s antineutriny - i tato reakce je možná, její účinný průřez je prakticky stejný jako v těch detektorech, samozřejmě pro antineutrina s energií řádově stejnou jako z těch reaktorů. Antineutrino samozřejmě musí mít aspoň takovou energii, aby umožnilo přeměnu protonu v neutron a ještě zbylo na produkci pozitronu. Srážkou protonu s antineutrinem vzniká pozitron a neutron - v detektorech se detekují obě částice, u pozitronu konkrétně gama fotony vzniklé po jeho anihilaci s elektronem, a z časové souvislosti mezi detekcí gama fotonů a neutronem se usuzuje na danou reakci. Účinný průřez této reakce pro antineutrina vznikající v jaderných reaktorech je cca 10^-47 m2, což si můžeme přiblížit následujícím zjednodušujícím příkladem - pokud předpokládáme příčný průřez protonu cca 10^-30 m2 (ve skutečnosti je zhruba dvakrát větší), tak to znamená, že protonem musí proletět cca 10^17 antineutrin, než jedno interaguje.
Ohledně té nové stabilní hmoty tvořené z něčeho jiného než z kvarků u a d, tak svého času se hypotetizovalo o možné existenci tzv. podivných hvězd, viz https://en.wikipedia.org/wiki/Strange_star . Podle těchto spekulací by hmota tvořená ve významné míře také z podivných kvarků, tedy kvarků s, mohla být přítomna v jádrech neutronových hvězd. Podivná hvězda by měla být o něco kompaktnější než neutronová hvězda, čistě teoreticky by bylo možno na ni usoudit pokud by pozorovaná neutronová hvězda byla při známé hmotnosti menší, než by podle teorie neutronová hvězda měla být. Na dolní limit velikostí neutronových hvězd usuzujeme z maximálních rychlostí otáčení pulsarů, které měříme podle frekvence těch pulzů - protože totiž obvodová rotační rychlost nemůže přesáhnout rychlost světla, z velikosti frekvence pulzů odvodíme maximální poloměr toho pulsaru. Dosavadní měření zatím neprokázala rozpor mezi stávajícím modelem standardních neutronových hvězd a frekvencí jejich pulzů, zatím tedy hypotéza podivných hvězd, a s ní i hypotéza existence nestandardní jaderné hmoty, zůstává pouze hypotézou.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Nedbal,2019-09-22 22:10:00
Vážení pánové,
děkuji. Reakce p-p ve slunci budou asi především ty tunelované, což je důvod klidného hoření sluníčka, vznik neutronu z protonu a antineutrina bude ve Slunci asi velmi minoritní. Mimochodem, je znémo, jaký je podíl neutrin a antineutrin? (Dávám stranou pana Majoranu)
Šance na vytvoření nějaké odlišné stabilní hmoty mimo té klasiceké jaderné z u,d, v našich normálních podmínkách asi nejsou, nebude tam asi žádné energetické minimum. Což je škoda, hodilo by se (například ty scifi reakce mionovou katalýzou, "neutronium" a podobně). Nějak mi to připadá trochu smutné, co se dá dělat.
P.N.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Brož,2019-09-23 01:10:53
Ohledně podílu neutrin a antineutrin ve vesmíru celkově, tak pokud předpokládáme existenci reliktních neutrin, kterých by mělo být zhruba tolik, jako reliktních fotonů, tedy řádově miliardkrát více než současných baryonů a leptonů, tak tam podíl mezi neutriny a antineutriny nebudeme znát do té doby, dokud nebudeme umět tato reliktní neutrina pozorovat. A to nebudeme umět ještě opravdu hodně dlouho.
Pokud by se nám nějakým zázrakem podařilo ve vzdálené budoucnosti zvýšit energie urychlovaných částic o nejméně osm řádů, tak bychom možná mohli začít registrovat první interakce mezi částicemi v urychlovacím tunelu a reliktními neutriny. Stěny urychlovače totiž odstíní reliktní fotony, takže ty se uvnitř tunelu nenachází, nicméně nemají šanci odstínit reliktní neutrina, která jsou uvnitř tunelu ve stejné hustotě, jako kdekoliv jinde ve vesmíru, tedy řádově jedno na milimetr krychlový. I tak by se ale jednalo o velice vzácné interakce, které bychom ale mohli detekovat díky tomu, že v urychlovači obíhá obrovské množství částic a mohou tam obíhat dlouho. Samotná obrovská energie částice ještě neznamená, že s reliktním neutrinem zainteraguje – registrujeme totiž kosmické částice o energiích blížících se až k 10^20 eV (viz https://en.wikipedia.org/wiki/Ultra-high-energy_cosmic_ray), které k nám podle všeho musely přiletět z kosmologických vzdáleností, tedy ze vzdáleností až stovek miliónů světelných let, a jelikož tuto cestu přežily, znamená to, že interakce i takto vysoce energetických částic s reliktními neutriny je extrémně málo pravděpodobná. Na druhou stranu ale takto vysoce energetických kosmických částic registrujeme řádově jednu za mnoho let, zatímco v tom urychlovači bychom jich mohli mít o mnoho řádů více. Postavení takovéhoto urychlovače bude ale ještě po hodně dlouhou dobu naprosté scifi, a je docela dobře možné, že bude i fyzikálně nemožné takovýto urychlovač realizovat na Zemi. Tak např. jeden ze zásadních problémů u urychlování částic v kruhových urychlovačích jsou energetické ztráty synchrotronových zářením – částice pohybující se po zakřivené dráze totiž ztrácí energii vyzařováním fotonů. Tyto problémy se dají obejít v lineárním urychlovači, ve kterém se ale pro změnu zase ztratí výhoda postupného urychlování v jednotlivých cyklech.
Jinými slovy, změření podílu reliktních neutrin a antineutrin ve vesmíru bude asi spíše úkol na příští století.
Možná Vás ale zajímá to, jestli je možné zjistit asymetrii v produkci neutrin a antineutrin. Neutrina a antineutrina se běžně rodí v odlišných typech procesů, které tím pádem nejde moc dobře přímo srovnávat, museli bychom dělat porovnání u exotičtějších druhů procesů, které jednotně produkují neutrina i antineutrina. Jedním z takových procesů je exploze supernovy, po níž vzniká neutronová hvězda. Pokud bychom proces vzniku neutronové hvězdy chápali jen jako proces, při kterém se slučují elektrony s protony za vzniku neutronů, tak bychom museli registrovat neutrina, protože právě neutrina, nikoliv antineutrina, vznikají v reakci p+e=n+ný. Už jsem dříve zmínil, že neutrina ze supernovy jsme zatím detekovali jenom jednou, v případě supernovy SN1987A (https://en.wikipedia.org/wiki/SN_1987A#Neutrino_emissions) – mimochodem, jenom proto, že šlo o velice blízkou supernovu, která explodovala ve Velkém Magelanově mračnu - a zachytilo se tehdy – a teď pozor – 25 antineutrin, a ani jedno neutrino. Jak je to možné? Neutrina se zachytávají v jiných procesech, než antineutrina, tyto reakce mívají odlišné pravděpodobnosti, a příslušné detektory prostě byly citlivější na detekci antineutrin. Jak ale mohla při vzniku neutronové hvězdy vzniknout antineutrina? Podle současných modelů totiž v závěrečné fázi gravitačního kolapsu zbytku hvězdy vzniká v jádře natolik obrovský tlak a teplota, že tam vznikají termální bozony Z, a ty se rozpadají symetricky na neutrina a antineutrina, přičemž těchto termálních párů neutrino-antineutrino vzniká až o několik řádů více, než kolik je neutrin vzniklých ze sloučení elektronů a protonů. Proto pokud budou někdy v budoucnu opět zachycena neutrina z nějaké další supernovy, budou to s největší pravděpodobností opět antineutrina. Pokud by ale někdy v hodně vzdálené budoucnosti umělo lidstvo při explozích relativně blízkých supernov detekovat reprezentativní vzorky (tedy rozhodně ne řádově desítky, ale aspoň řádově bilióny) jak antineutrin, tak neutrin, tak by se teoreticky dala začít sledovat nějaká statistika, jak se tato neutrina či antineutrina rodí. Ale to je nemenší scifi, než předchozí úvaha s tím urychlovačem detekujícím reliktní neutrina.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Nedbal,2019-09-23 17:12:14
Vážený pane Broži,
jen stručně; nějak jsem nepostřehl, jestli už je nějak dokázáno, zda jsou neutrina Fermiovská, nebo Majoranovská, zda tedy anti- a neutrina nejsou vlastně identická; to by mělo tedy i jakýsi kosmologický dopad,ne?
P.N.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Vladimír Wagner,2019-09-23 18:05:56
Zatím nebylo experimentálně rozhodnuto, zda jsou neutrina Majoranovská nebo Diracovská. Rozhodnout o tom může pozorování bezneutrinového dvojného rozpadu beta, tedy rozpadu, kdy vyletí dva elektrony , ale žádné neutrino. Vyzářené antineutrino se pohltí jako neutrino a kompenzuje tak vyzáření druhého antineutrina. Pokud tento rozpad zaznamenáme, tak musí být neutrino Majoranovské. Pokud budeme mít nějakou představu o hodnotě hmotnosti neutrina (závisí na ní pravděpodobnost tohoto jevu) a zjistíme, že nepozorujeme dvojný bezneutrinový rozpad beta z odpovídající pravděpodobností, tak prokážeme, že je Dirackovské.
Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Re: Ďakujem za odpoveď,
Pavel Brož,2019-09-23 18:34:42
Dobrý den, definitivně ještě nebyla otázka Diracovskosti či Majoranovskosti neutrin rozřešena, ale tuším že nedávno bylo opět zesíleno omezení plynoucí z bezneutrinového dvojitého beta rozpadu, který dodnes nebyl pozorován. Zjednodušeně řečeno, Majoranovská neutrina se v drtivé většině experimentů chovají identicky jako Diracovská, akorát že v některých svých stavech se chovají jako Diracovská neutrina, zatímco v jiných svých stavech jako Diracovská antineutrina. Zatímco Diracovské neutrino se nemůže vůbec nijak transmutovat na antineutrino a naopak, u Majoranovských se jedná pouze o dva různé stavy téže částice, mezi kterými může ve specifických interakcích přecházet. Bezneutrinový dvojitý beta rozpad je příkladem takovéto specifické interakce, zatím se ale nepozoroval.
Existují dokonce rozšíření standardního modelu, které obsahují mix obou kategorií neutrin, jak Diracovských, tak Majoranovských. Takovéto teorie mohou vzniknout z různých supersymetrických rozšířeních standardního modelu poté, co je spontánně narušena supersymetrie. V supersymetrických teoriích jsou totiž Majoranovská neutrina jako doma. Navíc zde existují mnohé algebraické souvislosti mezi oběma kategoriemi neutrin - tak např. dvě Majoranovská pole mohou být uspořádána tak, že jsou nerozlišitelná od Diracovského pole. Je to možné proto, že Diracovské pole je čtyřkomponentní, přičemž dvě komponenty popisují částici, a dvě zbylé antičástici, zatímco Majoranovské pole je dvoukomponentní. Proto je Majoranovské pole matematicky jednodušší, ba dokonce základnější objekt - v matematickém jazyce je Majoranovské pole popsáno tzv. spinorem, což je dvojice komplexních čísel s vhodnými transformačními vlastnostmi vůči Lorentzově grupě transformací (přesněji řečeno vůči její podgrupě, která neobsahuje žádná zrcadlení). Diracovské pole je oproti tomu popsáno bispinorem, dvojící spinorů, je tedy složitější.
V principu si tedy lze představit situaci, kdy rozšířená supersymetrická teorie v důsledku narušení supersymetrie v nejranějších okamžicích velkého třesku dala zrod efektivní teorii, kterou dnes známe jako standardní model a která obsahuje Diracovská neutrina, přičemž ale zbyl nějaký ten nespárovaný zbytek o dnes neznámé velikosti, který ze standardního modelu "vyčuhuje", tj. nepatří do něj, a který zůstal na dodatečná Majoranovská neutrina. Dnes je dokonce stále ještě přípustná možnost, že všechna neutrina mohou být Majoranovská. I když by se ale po dalších zpřesnění při hledání bezneutrinového beta rozpadu ukázalo, že všechna neutrina nemohou být Majoranovská (např. proto, že by z experimentu vycházela tak malá klidová hmotnost Majoranovských neutrin, že by to kolidovalo s kosmologickými daty, která nějakou nenulovou hodnotu pro součet klidových hmot neutrin určují), tak stále zůstane navždy otevřená otázka, jestli kromě těch Diracovských přece jen neexistují i nějaká Majoranovská neutrina, tzn. zda nemáme v teorii nějaký mix Diracovských a Majoranovských neutrin.
odhad
Roman Rodak,2019-09-16 15:02:11
Je aj nejaký predpoklad kde by sa postupné znižovanie horného limitu mohlo zastaviť, alebo je to informácia ktorú treba získať výlučne experimentom a nevieme či skončíme na 1 eV, 1 meV, alebo 1 neV? Narážam napr. na roky pred nájdením hmotnosti higgsovho bozónu, kedy bolo jasné, že buď bude mať rádovo stovky GeV, alebo bude nutné zásadne zmeniť štandardný model.
Re: odhad
Pavel Brož,2019-09-16 21:48:24
Pokud hledáme spodní limity na hmotnost nejlehčího neutrina jen s použitím omezení plynoucím ze stávajícího Standardního částicového modelu, tak jedinou spodní limitou je nula. To ale platí pouze pro hmotnost nejlehčího neutrina, na součet hmotností všech tří neutrin už máme netriviální odhady. Viz např. pátý odstavec v sekci Mass zde: https://en.wikipedia.org/wiki/Neutrino#Mass - pro absolutní hodnotu rozdílu čtverců hmotností neutrin 1 a 2 (což nejsou ani elektronová, ani mionová, ani tauonová neutrina, ale vlastní energetické stavy neutrin, odpovídající jejich kombinacím) dostáváme limit |delta m12^2|=0,000079 eV^2, a pro odpovídající rozdíl čtverců hmotností neutrin 2 a 3 potom |delta m32^2|=0,0027 eV^2. Takže pokud by např. neutrino 1 mělo nulovou klidovou hmotnost, tak potom neutrino 2 musí mít hmotnost odmocnina(0,000079)=0,0089 eV. Známe-li klidové hmotnosti vlastních stavů 1, 2 a 3, tak potom lze spočíst klidové hmotnosti elektronového, mionového a tauonového neutrina za použití tzv. Pontecorvo–Maki–Nakagawa–Sakata matice (viz https://en.wikipedia.org/wiki/Pontecorvo%E2%80%93Maki%E2%80%93Nakagawa%E2%80%93Sakata_matrix), jejíž elementy se ale bohužel určují neméně lehko, než ty hmotnosti neutrin.
Pokud ale nelpíme na hledání limitů určovaných čistě jen Standardním částicovým modelem, ale přibereme také modely pro jiné fyzikální oblasti (konkrétně Standardní kosmologický model), tak dostáváme i další spodní odhady - opět již ve zmíněné sekci https://en.wikipedia.org/wiki/Neutrino#Mass je uvedeno, že z dat získaných při studiu gravitačního čočkování galaktických clusterů vychází hodnota pro součet hmotností všech tří neutrin jako 1,85 eV. Pokud k tomu přidáme výše zmíněné odhady na rozdíly hmotností, znamenalo by to, že hmotnosti všech tří neutrin musí být k sobě velice blízké, pohybující se okolo hodnoty 1,85/3=0,617 eV.
Zde je ale nutné říct, že výsledky získané studiem gravitačního čočkování zároveň vyžadují splnění svých vlastních modelových předpokladů - jinými slovy, zatímco odhady zmíněné v prvním odstavci tohoto příspěvku bychom mohli uvést slovy: "Pokud platí Standardní částicový model ...", tak odhady z druhého odstavce by bylo zapotřebí uvést slovy: "Pokud platí Standardní částicový model PLUS pokud také platí Standardní kosmologický model ...".
Re: odhad
Vladimír Wagner,2019-09-16 22:30:47
Díky Pavlovi za odpověď, jen bych doplnil, že z druhého kvadrátu rozdílu hmotnosti neutrin vychází rozdíl mezi dvěma stavy neutrin 0,05 eV. Připomínám, že předpokládaná dosažitelná limita u KATRIN je 0,2 eV. Pokud je tedy správná interpretace gravitačního čočkování vzdálených galaxií, o které píše Pavel a hmotnost i elektronového neutrina bude okolo 0,6 eV, tak to KATRIN uvidí. Pokud ovšem je v této interpretaci nějaký zádrhel a degenerace hmotností není tak velká, pak by hmotnost byla v řádu 0,05 eV a méně, tak už bohužel pro KATRIN nebude dosažitelná. Bude pak potřeba najít úplně nový typ experimentu, případně spektrometru. Muselo by jít o spektrometry nové generace. Ty by pak v principu mohly rozlišit různé hmotnostní stavy neutrina.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce