Už je to asi tak dvacet let, co jsme zjistili, že náš vesmír se nejen rozpíná, ale tohle rozpínání se dokonce ještě zrychluje. Aby tohle bizarní chování vesmíru astrofyzici vysvětlili, tak si museli vymyslet temnou energii, tajuplnou esenci, která pohání zrychlování rozpínání vesmíru. Od té doby se všichni snaží přijít na to, co by taková temná energie mohla být zač. Pokud by se to fyzikům povedlo, tak prolomí jednu z největších fyzikálních záhad dnešní doby. Není ale tajemstvím, že veškeré snahy v tomto směru byly zatím vesměs neúspěšné.
Souvik Banerjee ze švédské Uppsalské univerzity a jeho kolegové vytvořili nový model vesmíru, který by podle nich mohl vyřešit problém s temnou energií. Jejich koncept vesmíru, který publikoval časopis Physical Review Letters, zahrnuje právě i temnou energii a nabízí vesmír, který sedí na rozpínající se bublině v extra dimenzi. Rekvizity modelu švédského týmu nezapřou, že mají co dělat se strunovými teoriemi.
Strunové teorie si přitom už řadu let dělají zálusk na to, že vysvětlí temnou energii i další ze záhad fyzikálního světa. Zároveň ale čelí kritice z mnoha různých stran, a někteří fyzici rádi zdůrazňují, že žádný z modelů, který vycházel ze strunových teorií, se zatím neukázal jako životaschopný.
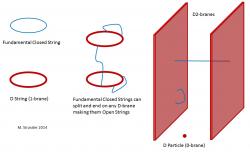
Banerjee a spol. vycházejí z toho, že náš vesmír existuje na takzvané bráně (brane). Veškerá existující hmota v našem vesmíru podle nich souvisí se strunami, které jedním koncem procházejí skrz bránu do další dimenze. Jak říká Wikipedia, brány jsou dynamické objekty ze světa strunových teorií, které se mohou šířit časoprostorem podle zákonitostí kvantové mechaniky. Brány mají hmotnost a mohou mít i další vlastnosti, jako třeba elektrický náboj.
Podle Banerjeeho týmu je gravitace našeho čtyřrozměrného časoprostoru spjatá s rozpínající se bránou, která zase úzce souvisí s překlopováním nesupersymetrického pětirozměrného anti-de Sitterovského falešného vakua na pravé vakuum. Nezní to zrovna moc srozumitelně, ale výsledkem toho prý je, že se pozorovatel ve čtyřrozměrném časoprostoru setkává s působením síly odpovídající pozitivní kosmologické konstantě spojené s hmotou a zářením. Což je přesně to, co pozorujeme.
Strunové teorie si v současné době nestojí příliš dobře. Výsledky experimentů a pozorování je nijak zvlášť nepodporují. Spíše naopak. Jestli s tím něco zmůže práce Banerjeeho týmu, to se ukáže až časem.
Video: What is a brane?
Literatura
Uppsala Universitet 27. 12. 2018, Physical Review Letters 121: 261301.
Zachrání nás teorie strun před protivnými Boltzmannovými mozky?
Autor: Stanislav Mihulka (25.05.2013)
Vyvěrá kvantová mechanika ze strunové teorie pole?
Autor: Stanislav Mihulka (07.11.2014)
Gravitační vlny připlavily realitu do snění o extra dimenzích
Autor: Stanislav Mihulka (15.09.2018)
Diskuze:
Jako laik se domnívám že cestovat ZPĚT v našem "čase" umí každá baryonová hmota
Karel Ralský,2018-12-30 20:02:28
jenže má to háček cestovat v našem čase lze jen v tom případě kdy ona událost vznikla(je to "téměř" bez energie od plynu, (přes hvězdy po černou díru) protože se tak děje na úkor energie budoucího času) a tak baryonová hmota podle hmotnosti(různost a rozdíly) cyklicky opakuje "cestování v našem čase" jen živá hmota se vymyká tomuto fenoménu protože v "našem čase(celý vesmír)" má svůj vlastní čas. Pozorovatel v jiné časoprostorové dimenzi by pozoroval celý náš vesmír třeba 1 desetinu sekundy jenže pro nás jsou to miliardy let.V takové entitě(spojených s naším vesmírem) musí existovat desítky dimenzí vezmeme li v úvahu Planckovu délku, až po rozměr celého vesmíru.
Re: Jako laik se domnívám že cestovat ZPĚT v našem "čase" umí každá baryonová hmota
Jiri Naxera,2018-12-31 22:27:08
Počkejte, to nechápu. Energie se pokud vím zachovává (lokálně), navíc jsou fyzikální zákony symetrické vůči otočení času naopak (přesněji CPT, ale to je teď jedno). Šipka času má asi něco společného s teorií pravděpodobnosti.
Ale ty jiné dimenze nechápu, co píšete. Co to je "pozorovatel v jiné časoprostorové dimenzi"? My žijeme (zjednodušeno do eukleidovského prostoru abych to nekomplikoval, dalo by se to rozšířit i pro zakřivený prostor v OTR, i když ne úplně triviálně) v 3rozměrném prostoru, to znamená, že existují právě tři lineárně nezávislé vektory (tzn. třetí vektor nelze vytvořit jako součet násobků prvního a druhého), pomocí jejichž násobků můžete jednoznačně popsat libovolný bod v našem prostoru.
Můžete nějak (klidně i slovně, bez lineární algebry co je za tím) popsat, co to je ta jiná dimenze? A jak by měla vidět "ty naše"?
BTW Planckovu délku bych do toho netahal, ta dimenzi nezvyšuje, spíš snižuje (podle všeho ve všech dostatečně pokročilých teoriích kvantové gravitace vychází mikroskopicky spektrální dimenze (jestli se nepletu souvisí s random walk a pravděpodobností návratu do počátku) 2, nikoli 4). Ale bez kvantování násobení konstantou dimenzi nemění.
Re: Re: Jako laik se domnívám že cestovat ZPĚT v našem "čase" umí každá baryonová hmota
Karel Ralský,2019-01-01 06:42:39
Začneme tím Planckem od něj se to totiž podle mé laické představy, odvíjí protože nejmenší časovou jednotku už nelze ani dělit a domnívám se, že šipka času která směřuje od této jednotky má "nekonečně" mnoho variant v naší dimenzi musí projít téměř "deseti řády" aby "energie" byla délkou a téměř 22 řády aby se "energie"(jiná než v naší dimenzi) proměnila v nějakou hmotnost a to jsme nezačali ani atomem či molekulou v naší dimenzi.
V každém bodě našeho vesmíru(naší dimenzi) se nachází určitá časoprostorová délka, která se cyklicky opakuje tím vznikne "hmotnost" v našem časoprostoru(vesmíru) jenže tato délka může mít kladnou nebo zápornou hodnotu, takže naše atomy mohou být pro někoho "hvězdou" a naše hvězda může být zase "atomem" byť v jiné formě než naší fyziky a dostali jsme se k těm dimenzím a to buď prostorová(proto jsem psal o té zemi, která je uvnitř větší), viz výše nebo časová, a my mezi tím tak trochu plaveme(proto jsem psal o té časové anomálii návratu v čase) v prostoročasové dimenzi řízenou "našimi" fyzikálními zákony a NAŠÍ místní energií včetně gravitace.A myslím si že prostorových a časových dimenzí spojených s naším vesmírem mohou být jednotky nebo desítky a ne všechny jsou "pohostinné" jako ta naše.
Pozemskou matematiku jsem si "zakázal" v 15letech a řídím se vlastním možná nedokonalým rozumem.
A myslím si že gravitace v kvantové fyzice pro nás není podstatná protože máme takovou rychlost že "mávnutím ruky překonáme miliardy atomů " nebo prostým růstem překonáváme rychlost, která udržuje atomy a elektrony na "orbitě". Ovšem když se ty miliardy hmoty spojí horko těžko překonáváme vlastní váhu. Protože délka která vytváří návrat v čase(hmota) se neustále pro nás nepatrně zkracuje máme tady gravitaci.
Vyskúšať treba všetko.
Richard Pálkováč,2018-12-29 08:21:09
Treba vyskúšať všetky možnosti vysvetlenia v článku uvedenej záhady. Keď to inak nejde, tak aj pomocou strún, superstrún, membrán a dimrenzíí skrútených do malého kruhu. Nemyslím, že by sme niečo z toho mohli v súčasnosti označiť za nezmysel, keďže o tom v podstate nič nevieme.
Ja sa na tieto veci, ale pozerám podstatne jednoduchšie a realistickejšie. Mám už "jasno", aj vo vesmíroch v iných dimenziách (http://riki1.eu/vesmiry.htm) aj v podstate tmavej energie a tmavej hmoty (http://riki1.eu/zaporna_temna_tmava_energia_hmota.htm).
Ešte niečo k prirovnaniam typu "keby ľudia žili na papieri (teda by boli 2D)". Prosím uvedomte si,že takéto prirovnania sú nezmyselné, pretože reálne objekty sú vždy len 3D. Žiadne 1D, 2D objekty reálne neexistujú, sú len výsledkom matematickej alebo geometrickej abstrakcie v mysli inteligentnej bytosti. Podľa môjho názoru dokonca neexistujú ani 4D, 5D ... objekty, ale to je už len môj názor.
Re: Vyskúšať treba všetko.
Milan Krnic,2018-12-29 16:11:07
Klasicky, neexistují, dokud je někdo nedokáže. Na to tmavé cosi lze uplatnit stejný postup, jenže co by pak ta fůra lidí dělala ...
Re: Vyskúšať treba všetko.
Jiri Naxera,2018-12-29 17:06:06
Tak vzhledem k matematické abstrakci používané v současných teoriích...
Vezměte obyčejnou kulatou tužku, bez popisek, a nějak jí hejbejte sem a tam v našem obvyklém 3D (+1D čas, ale ten eukelidovsky berme za nezávislou proměnnou) prostoru.
A teď si představte bod, který se pohybuje v 5D prostoru netriviální topologie (R^3 x S2) - a ten bod je taky ta naše stará známá tužka.
A když na ní něco napíšete takže záleží i jak je natočená kolem vlastní osy, tak máte dokonce 6 stupňů volnosti a pro popis tím pádem bod v 6D prostoru (R^3 x SO(3))
Re: Re: Vyskúšať treba všetko.
Florian Stanislav,2018-12-29 20:13:03
Nerozumím, co píše J.Naxera :
"A když na ní něco napíšete takže záleží i jak je natočená kolem vlastní osy, tak máte dokonce 6 stupňů volnosti a pro popis tím pádem bod v 6D prostoru (R^3 x SO(3))"
6 stupňů volnosti je v podstatě možnost nezávislé rotace podle osy x,y,z a nezávislé posuny podle osy x, y, z.
Nejde tedy o 6 dimenzí prostoru, ale o počet nezávislých os, zde 6 os.
https://is.muni.cz/th/b3t5f/Bakalarska_prace.pdf
Redundantním objektem ( více než 6 stupňů volnosti) je právě lidská ruka se sedmi
stupni volnosti. [9] Lidské tělo má přibližně 206 kostí a 600 svalů, a kdyby bylo plně
namodelované, mělo by kolem dvou set stupňů volnosti. [3]
Pokud se nepletu, tak konec prstu má 27 stupňů volnosti (27 nezávislých os by tento pohyb mohlo nahradit, kdy to byl nějaký robot) vzhledem k dalším možnostem pohybu celého těla s koncem prstu na ruce.
Nerozumím odkazu R.Pálkovače :
http://riki1.eu/dimenzie.htm
"Z toho vyplýva, že aj každý priestorový rozmer 3D priestoru, môžeme zakriviť do ďalších dvoch. Máme teda 9 priestorových a 1 časový rozmer, čiže dokopy 10 D priestor."
Teorie superstrun
https://cs.wikipedia.org/wiki/Teorie_superstrun
"Podle teorie superstrun má vesmír – namísto nám dobře známých čtyř rozměrů – jedenáct rozměrů (jeden časový a deset prostorových). Dodatečné rozměry jsou ovšem svinuty do variety malé velikosti, v důsledku čehož unikají přímému pozorování."
Takže 11 dimenzí, které kromě 4 unikají pozorování.
Re: Re: Re: Vyskúšať treba všetko.
Richard Pálkováč,2018-12-29 21:33:10
Môj článok nemá nič spoločné s teóriou strún, ani superstrún. Snaží sa len obecne vysvetliť, prečo by náš vesmír (ako celok) nemal byť obmedzený iba tromi priestorovými rozmermi, aj keď predstavivosť našej mysle, je obmedzená len na 3 priestorové rozmery, plus jeden časový rozmer.
Myslím, že pán Naxera nemal na mysli stupne voľnosti ale jednoznačne matematicky popísateľné priestorové dimenzie, aj keď len v rovine matematickej abstrakcie.
Re: Re: Re: Re: Vyskúšať treba všetko.
Florian Stanislav,2018-12-30 00:55:36
Nevím, co chápete jako dimenze. Obrázek
http://riki1.eu/1dto3d.jpg
na
http://riki1.eu/dimenzie.htm
Skoro to vypadá, že prostor chápete jako nějaký roh krychle, a že když z té krychle vybočíme, tak jsme v jiném prostoru. I v primitivnějším případě, že jsme v rovině s osami x a y, můžeme vybočit kamkoliv v té rovině, tedy i do záporných hodnot, takže představa nějakého drformovaného drátu, je k ničemu.
Lidé vynalezli záporná čísla a drát má délku kladnou.
Když lineární drát v ose x zakroutím, tak místo nulových hodnot souřadnic y, z bude mít nějaké hodnoty pro dané body, které pochopitelně leží stále v 3D prostoru. Takže nevybočujete z 3D prostoru do dalších prostorů, ale z reality.
Re: Re: Re: Re: Re: Vyskúšať treba všetko.
Richard Pálkováč,2018-12-30 09:13:59
Priestor síce nechápem ako roh kocky, ale áno, snažím sa vybočiť z našej 3D reality, napríklad v záujme vysvetlenia tmavej hmoty. Konkrétnejšie to popisujem tu http://riki1.eu/vesmiry.htm
Re: Re: Re: Re: Re: Re: Vyskúšať treba všetko.
Florian Stanislav,2018-12-30 11:19:59
Dobře, začal jsem to tento týden chápat. Drátek ve směru osy se stáčí do dvou dalších nepostřehnutelných dimenzí prostoru.
Mám podobné zkušenosti, opakovaně zlobí kontakt venkovního zvonku. Asi se někam neviditelně stočil.
Re: Re: Re: Re: Re: Re: Re: Vyskúšať treba všetko.
Richard Pálkováč,2018-12-30 14:26:02
Nie, drôtik Vášho zvončeka, nebude stočený do ďalšej priestorovej dimenzie:)
V mojom článku drôtik, priamku, používam len ako príklad 1D priestoru. Keď tento zakryvíme ako popisujem, tak získame 3D priestor. Ďalej už zakryvujem dimenzie získaného priestoru. Snažím sa čitateľovi poskytnúť len vizuálnu pomôcku z predchádzajúceho príkladu s priamkou a tak tieto dimenzie na prvýkrát tiež zakryvujem každú do dvoch ďalších dimenzií, ale hneď nato píšem, že to môže byť do hocikoľko ďalších.
Nesmiete sa na mňa hnevať, že to nezobrazujem, alebo neopisujem úplne jasne, nejakým obrázkom. Toho totiž nikto na svete zatiaľ žiaľ nie je schopný, máme totiž "zabetónované" naše mozgy v 3D. Mne je teda jasné, že by som prakticky nemal byť schopný takýchto predstáv, ale predsa sa o to budem snažiť a nevzdám to, kým mi to bude dávať zmysel.
Pokiaľ by mi bol niekto od detstva vnucoval myšlienku viacerých priestorových dimenzií, tak by som bol na tom asi podstatne lepšie a možno dnes by som bol génius, čo vidí viac priestorových dimenzií ako sú 3. Ale to nie som.
Matematicky si môžete modelovať viac dimenzionálne "priestory", stačí povedzme pridať tlak a teplotu ako ďalšie dimenzie, prípadne Vami spomínané stupne voľnosti. To ale nebudú priestorové dimenzie, jedine tak priestoru podobné ako v prípade času.
Ak dôjdem k nejakým novým poznatkom, tak ich zase napíšem do článku, ale zatiaľ je toto všetko čo viem. Zaoberám sa tým len 2 roky a dôvodom prečo sa tomu venujem, je záhada tmavej hmoty.
Re: Re: Re: Vyskúšať treba všetko.
Jiri Naxera,2018-12-29 23:46:03
Byla to reakce na něco jako "1D 2D 4D 5D neexistují"
" Nejde tedy o 6 dimenzí prostoru, ale o počet nezávislých os, zde 6 os."
Však píšeme o tom samém, jen z jiného úhlu pohledu. Vy říkáte, že polohu nějakého pevného předmětu je možné určit šesti čísly (a používáte konkrétní bázi posuv_x, posuv_y, posuv_z, rotace_podel_x, rotace_podel_y, rotace_podle_z).
Já akorát říkám, že s trochou abstrakce se to dá považovat za vektor v nějakém 6D prostoru (varietě), který je topologicky izomorfní k R^3 x SO(3) {tři reálné osy a rotační grupa v 3D prostoru).
V tomhle případě se můžeme úspěšně bavit o tom, že co je "reálné" a co "abstrakce" a poslat mě do háje, že takhle se dá vymyslet úplně cokoli a žádný vícerozměrný prostor to není, ale jak roste složitost tak někde nastane okamžik kdy se tenhle rozdíl setře.
Např. klasický holografický princip, kde máme nějaký 4D uzavřený prostor, jehož okraj je tím pádem 3D a existuje nějaká korespondence mezi nimi - je reálnější to, co se děje v pixelech na 3d povrchu, nebo v 4d objemu? Zjevně je to nefyzikální otázka a "správná" odpověď bude záležet na tom, kolik dimenzí si uvědomují myslící bytosti, které v tom případně vzniknou. Ale co v případě, že vznikne inteligentní život v obojím? My řekneme že 3d a nic než 3d neexistuje, 4D ufouni se na jejich 4-Oslu budou bít do krve, že existuje jen 4d a zbytek je výmysl matematiků kteří se nuděj.
Strunové teorie
Jaroslav Crha,2018-12-28 21:18:13
Strunové teorie jsou blbost, protože v celém konceptu jim chybí parametr setrvačnosti. Tudíž by objekty procházející bránou museli nekonečně krát rychle zrychlit na nekonečnou rychlost aby poté za nekonečně krátkou dobu zpomalit, což by vedlo k totální likvidaci na subatomární úrovni. Navíc by takový transport vyžadoval několik nekonečen energie.
Re: Strunové teorie
Milan Krnic,2018-12-28 21:33:59
Mě by zajímalo, čím jsou tvořeny ty struny a brány. Mají z toho takový zvěřinec, že už by bylo dobré hledat základ :)
Doufám, že alespoň mají na univerzitě dobrou kávu. Pak se i z kanclu skvěle zkoumá (tak ale ono ostatně co jiného jim zbývá ...).
Re: Re: Strunové teorie
Hogigo Hogigo,2018-12-28 23:25:51
Struny mají být údajně tvořeny čistou energií (ne že bych si myslel, že je teorie superstrun pravdivá).
Re: Re: Re: Strunové teorie
Jiri Naxera,2018-12-29 03:37:15
Někde jsem slyšel přiblížení, že (super)struna se dá představit jako topologický defekt v časoprostoru. Ta energie odpovídá pak napětí a vibračnímu modu (a protože je ta struna kvantová, tak nemůže mít nulovou energii)
Re: Strunové teorie
Andrej M.,2018-12-29 01:24:39
pri teórii strún a temnej hmote ma vždy napadne ekvivalentný klasický príklad - keby žili ľudia na dvojrozmernom papieri, tak akýkoľvek zásah z 3 rozmeru by bol pre nich nepochopiteľný a akokoľvek by sa ho snažili pochopiť, tak by nemali šancu - je to skrátka mimo ich vesmír. Pre nich by bol človek v 3 rozmere rovný Bohu. Ešte relatívne "pár" rokov dozadu si ľudia mysleli že hviezdy sú dierky v nebeskej sfére, cez ktoré presvitá svetlo. Teraz sme trochu pokročili no v konečnom dôsledku je pre ľudí zatiaľ výsledok ten istý. Pokiaľ táto civilizácia vydrží tak potrvá zopár tisíc rokov než príde na podstatu hmoty a vesmíru a tieto teórie sa budú budúcim generáciám zdať ako tá teória o deravej nebeskej sfére. :-)
Re: Re: Strunové teorie
Jiri Naxera,2018-12-29 02:57:32
Kdyby žili opravdu na 2D papíru, tak i kdyby byl nakrásně v nějakém 3D prostoru, tak by o něm nikdo v tom 3D prostoru nevěděl (protože by byl nekonečně tenkej)
Re: Re: Strunové teorie
Marek Fucila,2019-01-02 03:40:14
Nie je to tak beznádejné, ako sa zdá. Objekty tretej dimenzie prechádzajúce dvojrozmenou plochou by mali nejaké konečné a predvídateľné vlastnosti.
My v 3D svete by sme štvorrozmerné objekty našich rozmerov pri ich prechode pozorovali.
https://fikacek.blog.idnes.cz/blog.aspx?c=683448
https://fikacek.blog.idnes.cz/blog.aspx?c=686012
A možno žijeme v 4D:
https://fikacek.blog.idnes.cz/blog.aspx?c=684408
Re: Strunové teorie
Jiri Naxera,2018-12-29 03:32:09
Uvědomujete si, co to je (mem)brána v rámci strunové teorie? Prostě n-rozměrná membrána, 1-brane je klasický string, 2-brane je 2rozměrná membrána (tedy to, co si pod tím normálně představíme) atd.
Takže tím neprocházejí žádné objekty jako v případě hvězdné brány, ale jsou na ně fixovány konce (super)stringů, žádné nekonečné zrychlění se nekoná atd. To D je od Dirichletových okrajových podmínek
Jinak k setrvačnosti, když vezmete klasickou OTR (která samozřejmě setrvačnost "umí" jako komplet gravitaci) a přidáte k tomu jeden další rozměr smotaný do malého kruhu, tak Vám z toho vypadne Kaluza-Klein teorie, která kromě gravitace popisuje i elekrromagnetismus - a opět setrvačnost funguje.
Klasickou stringovou teorii dostanete, když k tomu místo jednoho rozměru přidáte rovnou rozměrů šest, které musíte taky nějak srolovat - zpočátku se uvažovaly Calabi-Yau manifoldy (jestli si pamatuju, tak podstatné je že je na nich možné najít metriku s nulovým Ricciho tensorem, takže to opět sedne do OTR), takže setrvačnost opět zůstává.
Diskuze je otevřená pouze 7dní od zvěřejnění příspěvku nebo na povolení redakce